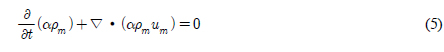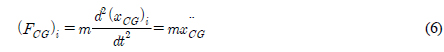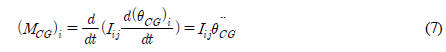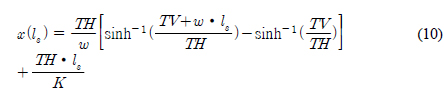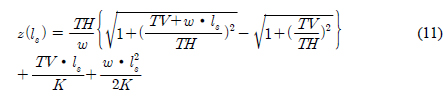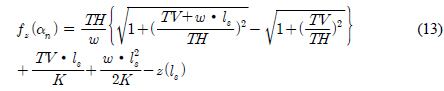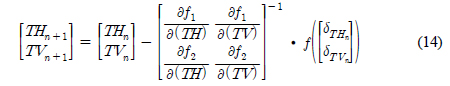1. ņä£ ļĪĀ
ĒŖ╣ņĀĢ ĒĢ┤ņŚŁņŚÉ ļ©Ėļ¼┤ļź┤ļ®░ ņśżļ×£ ĻĖ░Ļ░ä ņ×æņŚģņØä ņłśĒ¢ēĒĢśļŖö ļČĆņ£ĀņŗØ ĒĢ┤ņ¢æĻĄ¼ņĪ░ļ¼╝ņØś ĒŖ╣ņä▒ņāü ņĀĢĒÖĢĒĢ£ ņÜ┤ļÅÖņØæļŗĄĒŖ╣ņä▒ ļ░Å ņ£äņ╣śņ£Āņ╣śņä▒ļŖźņØ┤ ņÜöĻĄ¼ļÉ£ļŗż. ĒŖ╣Ē׳ ņ£äņ╣ś ņ£Āņ¦Ć ņä▒ļŖźņØĆ ĻĄ¼ņĪ░ļ¼╝ņØś Ļ░ĆļÅÖļźĀņØ┤ļéś ņ×æņŚģļŖźļźĀņŚÉ Ēü¼Ļ▓ī ņśüĒ¢źņØä ļ»Ėņ╣śĻĖ░ ļĢīļ¼ĖņŚÉ ļ¦żņÜ░ ņżæņÜöĒĢ£ ņÜöņåīņØ┤ļŗż. ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö Ēīīļ×æ ņżæ ĒĢ┤ņ¢æĻĄ¼ņĪ░ļ¼╝ņØś ņ£äņ╣śļź╝ ņ£Āņ¦ĆĒĢśĻĖ░ ņ£äĒĢ┤ Ļ│äļźś ņŗ£ņŖżĒģ£ņØä ņé¼ņÜ®ĒĢśņśĆņ£╝ļ®░, ĻĘĖ ņżæņŚÉņä£ ĒśäņłśņäĀ Ļ│äļźś(catenary mooring)ļź╝ ņé¼ņÜ®ĒĢśņśĆļŗż.
ļČĆņ£ĀņŗØ ĒĢ┤ņāüĻĄ¼ņĪ░ļ¼╝ ļ░Å Ļ│äļźś ņŗ£ņŖżĒģ£ņØś ņäżĻ│ä ļ░Å ņä▒ļŖź Ļ▓Ćņ”ØņØä ņ£äĒĢ┤ņä£ļŖö ņØ╝ļ░śņĀüņ£╝ļĪ£ ļ¬©ĒśĢņŗżĒŚś ļ░Å ĒżĒģÉņģ£(potential)ĻĖ░ļ░śņØś ņłśņ╣ś ĻĖ░ļ▓ĢņØä ņØ┤ņÜ®ĒĢ£ ņŚ░ĻĄ¼Ļ░Ć ļ│┤ĒÄĖņĀüņØ┤ļŗż.
Hong et al.(1988)ņØĆ Ļ│äļźśļÉ£ ļ░śņ×ĀņłśņŗØ ņŗ£ņČöņäĀņØś ĻĘ£ņ╣ÖĒīī ņżæ ņÜ┤ļÅÖĒŖ╣ņä▒Ļ│╝ ĒśäņłśņäĀ Ļ│äļźśņäĀņØś ņØĖņןļĀźņØä ņŗżĒŚśņØä ĒåĄĒĢ┤ Ļ│äņé░ĒĢśĻ│Ā ņØ┤ļź╝ 3ņ░©ņøÉ ĒżĒģÉņģ£ ņØ┤ļĪĀņØś ņłśņ╣śĒĢ┤ņäØņØä ĒåĄĒĢ┤ ļ╣äĻĄÉĒĢśņśĆļŗż.
Sirnivas et al.(2016)ņØĆ ļČĆņ£Āņ▓┤ņÖĆ Ļ│äļźś ņŗ£ņŖżĒģ£ņØś ņŚ░ņä▒ņÜ┤ļÅÖņŚÉ ļīĆĒĢ┤ ĒżĒģÉņģ£ ĻĖ░ļ░śņØĖ ĒöäļĪ£ĻĘĖļשņØä Ļ░£ļ░£ĒĢśĻ│Ā ņØ┤ļź╝ ņāüņÜ®ĒöäļĪ£ĻĘĖļשĻ│╝ ņŗżĒŚśņØä ĒåĄĒĢ┤ ļ╣äĻĄÉ ļ░Å Ļ▓Ćņ”ØĒĢśņśĆļŗż.
ņĄ£ĻĘ╝ ņĀäņé░ņ£Āņ▓┤ņŚŁĒĢÖņØś ļ░£ļŗ¼ļĪ£ ņØĖĒĢ┤ ņ£Āņ▓┤ļÅÖņŚŁĒĢÖ(Hydrodynamic) ļČäņĢ╝ņŚÉņä£ ļ¬©ĒśĢņŗżĒŚśņØś ĒĢ£Ļ│äļź╝ ļ│┤ņÖäĒĢśĻ│Ā ĒżĒģÉņģ£ ĻĖ░ļ░śņØś ņłśņ╣śĒĢ┤ņäØĻ│╝ ļ╣äĻĄÉĒĢśņŚ¼ ļ│┤ļŗż ņĀĢļÅä ļåÆņØĆ ĒĢ┤ņäØņØä ņ£äĒĢ£ ņĀæĻĘ╝ņØ┤ Ļ░ĆļŖźĒĢ┤ņĪīļŗż.
Ok et al.(2017)ņØĆ ņśżĒöłņåīņŖż CFD ĒöäļĪ£ĻĘĖļשņØä ņé¼ņÜ®ĒĢśņŚ¼ Ēīīļ×æ ņżæ ļŗ©ņØ╝ņäĀņ▓┤ ļ░Å ļ│æļĀ¼ ļ░░ņ╣śļÉ£ ļæÉ ļČĆņ£Āņ▓┤ņØś ņÜ┤ļÅÖņŚÉ Ļ┤ĆĒĢ┤ ņłśņ╣śĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśņśĆļŗż.
Wu et al.(2016)ņØĆ ņ×Éņ▓┤ Ļ│äļźś ņŗ£ņŖżĒģ£ ļ¬©ļōłņØä Ļ░£ļ░£ĒĢśĻ│Ā ņØ┤ļź╝ ņāüņÜ® CFD ĒöäļĪ£ĻĘĖļשņØĖ STAR CCM+Ļ│╝ ņŚ░ņä▒ņØä ĒåĄĒĢ£ ļČĆņ£Āņ▓┤ņÖĆ Ļ│äļźś ņŗ£ņŖżĒģ£ņØś ņÜ┤ļÅÖĒŖ╣ņä▒ņØä ĒīīņĢģĒĢśņśĆļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ĒśäņłśņäĀ Ļ│äļźś ņŗ£ņŖżĒģ£ņØś ņżĆņĀĢņĀü ĒĢ┤ņäØ ļØ╝ņØ┤ļĖīļ¤¼ļ”¼ļź╝ Ļ░£ļ░£ĒĢśĻ│Ā ņØ┤ļź╝ ņśżĒöłņåīņŖż CFD ĒöäļĪ£ĻĘĖļשņØĖ Open-source Field Operation And Manipulation(OpenFOAM)Ļ│╝ņØś ņŚ░ņä▒ņØä ĒåĄĒĢ┤ ļČĆņ£Āņ▓┤ņÖĆ Ļ│äļźś ņŗ£ņŖżĒģ£ Ļ░äņØś ņ¢æļ░®Ē¢ź ņŚ░ņä▒ ļ¬©ļōłņØä Ļ░£ļ░£ĒĢśņśĆļŗż. ņŚ¼ĻĖ░ņä£ Ļ│äļźśņäĀņØś Ļ┤Ćņä▒Ļ│╝ ņ¢æļĀź ĒÜ©Ļ│╝ļŖö Ļ│ĀļĀżļÉśņ¦Ć ņĢŖņĢśļŗż. Ļ░£ļ░£ļÉ£ ļ¬©ļōłņŚÉ ļīĆĒĢ£ ļ╣äĻĄÉ ļ░Å Ļ▓Ćņ”ØņØä ņ£äĒĢ┤ ļČĆņ£Āņ▓┤ ņÜ┤ļÅÖ Ļ│äņé░ņØä ņ£äĒĢ£ ņāüņÜ®ĒöäļĪ£ĻĘĖļשņØĖ AQWAņÖĆ Ļ│äļźśņäĀņØś ņןļĀź Ļ│äņé░ņØä ņ£äĒĢ£ ņāüņÜ®ĒöäļĪ£ĻĘĖļשņØĖ Orcaflexļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ņłśņ╣śĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśņśĆļŗż. ļæÉ ĒöäļĪ£ĻĘĖļשņØä ņäĀĒāØĒĢ£ ņØ┤ņ£ĀļŖö AQWAļŖö ĒżĒģÉņģ£ ĻĖ░ļ░śņØś Ļ▓ĮĻ│äņÜöņåīļ▓ĢņØä ņØ┤ņÜ®ĒĢ£ Ēīīļ×æ ņżæ ļČĆņ£Āņ▓┤ņØś ņÜ┤ļÅÖĻ│äņé░ ĒöäļĪ£ĻĘĖļשņ£╝ļĪ£ņä£ ņ£Āņé¼ĒĢ£ ĻĖ░ļŖźņØä Ļ░Ćņ¦ä ļŗżļźĖ ĒöäļĪ£ĻĘĖļשņŚÉ ļ╣äĒĢ┤ ļ▓öņÜ®ņä▒ņØ┤ Ļ░Ćņן ļåÆĻĖ░ ļĢīļ¼ĖņØ┤Ļ│Ā, OrcaflexļŖö Ļ│äļźśņäĀņØś ļÅÖņĀü Ļ▒░ļÅÖņØä Ļ│äņé░ĒĢśļŖö ĒöäļĪ£ĻĘĖļש ņżæņŚÉ ļ╣äņäĀĒśĢ ņÜöņåīļōżņØä ņČöĻ░ĆĒĢĀ ņłś ņ׳ļŖö ĒÖĢņןņä▒ņØ┤ Ļ░Ćņן ļåÆĻĖ░ ļĢīļ¼ĖņŚÉ ņČöĒøä ļ│Ė ņŚ░ĻĄ¼ņØś ĒÖĢņןņŚÉ ļīĆņØæĒĢśĻĖ░ ņ£äĒĢ©ņØ┤ļŗż.
2. ņżĆņĀĢņĀü ĒĢ┤ņäØĒöäļĪ£ĻĘĖļשņØś Ļ░£ļ░£
2.1 ņ¦Ćļ░░ļ░®ņĀĢņŗØ
ļ│Ė ņ£ĀļÅÖņןņØś ņ£Āņ▓┤ļŖö ļ╣äņĢĢņČĢņä▒┬ĘņĀÉņä▒ņ£Āņ▓┤ņØ┤ļ®░ ņ£ĀļÅÖņןļé┤ņØś ņ£ĀļÅÖņŚÉ ļīĆĒĢ£ ņåŹļÅäņÖĆ ņĢĢļĀźņØä Ļ│äņé░ĒĢśĻĖ░ ņ£äĒĢ┤ ņŚ░ņåŹļ░®ņĀĢņŗØĻ│╝ Navier-Stokes ļ░®ņĀĢņŗØņØä ņé¼ņÜ®ĒĢśņśĆļŗż. Ļ░üĻ░üņØś ļ░®ņĀĢņŗØņØĆ ņŗØ (1), (2)ņÖĆ Ļ░Öļŗż.
ņŚ¼ĻĖ░ņä£ uļŖö ņ£ĀļÅÖņןņØś ņ£Āņ▓┤ņåŹļÅä, ŽüļŖö ļ░ĆļÅä, tļŖö ņŗ£Ļ░ä, pļŖö ņĢĢļĀź, ╬╝ļŖö ņĀÉņä▒Ļ│äņłś, gļŖö ņżæļĀźĻ░ĆņåŹļÅä, ņĢäļל ņ▓©ņ×É mņØĆ ļ¼╝Ļ│╝ Ļ│ĄĻĖ░ļĪ£ Ēś╝ĒĢ®ļÉ£ ņ£Āņ▓┤ņØś ļ¼╝ņä▒ņ╣śļź╝ ļéśĒāĆļéĖļŗż. ņ£Āņ▓┤ Ļ░äņØś ĻĄ¼ļČäņØĆ Ļ▓®ņ×É ļé┤ņŚÉ ņ░©ņ¦ĆĒĢśļŖö ņ▓┤ņĀüļ╣äņ£©ņØĖ ╬▒ļź╝ ĒåĄĒĢ┤ ņ×Éņ£Āņłśļ®┤ņØä ņłśņ╣śņĀüņ£╝ļĪ£ Ēæ£ĒśäĒĢśļŖö VOF(Volume of fluid) ĻĖ░ļ▓ĢņØä ņé¼ņÜ®ĒĢśņśĆļŗż. Ļ▓®ņ×ÉĻ░Ć ļ¼╝ļĪ£ ņÖäņĀäĒ׳ ņ▒äņøīņ¦ä Ļ▓ĮņÜ░ ╬▒ = 1, Ļ│ĄĻĖ░ļĪ£ ņÖäņĀäĒ׳ ņ▒äņøīņ¦ä Ļ▓ĮņÜ░ ╬▒ = 0, ņ×Éņ£Āņłśļ®┤ņØś ņ▓┤ņĀüļ╣äņ£©ņØĆ 0 Ōēż ╬▒ Ōēż 1 ļĪ£ ļéśĒāĆļéĖļŗż. ļæÉ ņ£Āņ▓┤ņØś ļ░ĆļÅäņÖĆ ņĀÉņä▒ņØĆ ņŗØ (3), (4)ņÖĆ Ļ░Öļŗż.
ņŚ¼ĻĖ░ņä£ ņĢäļל ņ▓©ņ×É aļŖö Ļ│ĄĻĖ░ wļŖö ļ¼╝ņØä Ļ░üĻ░ü ņØśļ»ĖĒĢśļ®░ ņ£ĀļÅÖņןļé┤ņŚÉņä£ ņ£ĀļÅÖņŚÉ ĒØÉļ”äņŚÉ ļö░ļźĖ ņ×Éņ£Āņłśļ®┤ņØä Ļ│äņé░ĒĢśĻĖ░ ņ£äĒĢ£ ļ│Ćņłś ╬▒ņØś ļ│ĆĒÖöļŖö ņØ┤ņåĪļ░®ņĀĢņŗØņØĖ ņŗØ (5)ņÖĆ Ļ░ÖņØ┤ ņĀĢņØśļÉ£ļŗż.
2.2 6ņ×Éņ£ĀļÅä ņÜ┤ļÅÖ
Ļ░Ģņ▓┤ļĪ£ Ļ░ĆņĀĢĒĢ£ ļČĆņ£Āņ▓┤ņØś 6ņ×Éņ£ĀļÅä ņÜ┤ļÅÖņØĆ ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ļéśĒāĆļé╝ ņłś ņ׳ļŗż.
ņŗØ (6)ņØĆ
x,
y,
z ļ░®Ē¢źņØś ļ│æņ¦ä ņÜ┤ļÅÖ ļ░®ņĀĢņŗØņØ┤Ļ│Ā, ņŗØ (7)ņØĆ
x,
y,
zņČĢņŚÉ ļīĆĒĢ£ ĒÜīņĀä ņÜ┤ļÅÖ ļ░®ņĀĢņŗØņØ┤ļŗż.
mĻ│╝
IijļŖö Ļ░üĻ░ü ļČĆņ£Āņ▓┤ņØś ņ¦łļ¤ēĻ│╝ Ļ┤Ćņä▒ļ¬©ļ®śĒŖĖņØ┤Ļ│Ā
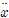
ņÖĆ
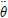
ļŖö ļČĆņ£Āņ▓┤ņØś ļ│æņ¦ä, ĒÜīņĀä ļ░®Ē¢źņØś Ļ░ĆņåŹļÅä ņä▒ļČä ļ│ĆĒÖöļ¤ēņØä ļéśĒāĆļéĖļŗż.
xCG ,
╬ĖCGļŖö Ļ░üĻ░ü ļČĆņ£Āņ▓┤ņØś ļ│æņ¦ä ņÜ┤ļÅÖĻ│╝ ĒÜīņĀäņÜ┤ļÅÖ ļ│Ćņ£äļź╝ ļéśĒāĆļé┤ļ®░
FCG ņÖĆ
MCGļŖö Ļ░üĻ░ü ļČĆņ£Āņ▓┤ņØś ļ¼┤Ļ▓ī ņżæņŗ¼ņŚÉ ņ×æņÜ®ĒĢśļŖö ļ│æņ¦ä ņÜ┤ļÅÖĻ│╝ ĒÜīņĀäņÜ┤ļÅÖņØś ĒלĻ│╝ ļ¬©ļ®śĒŖĖļź╝ ļéśĒāĆļéĖļŗż. ņŚ¼ĻĖ░ņä£
FCGņÖĆ
MCGļŖö ņŗØ (8), (9)ņÖĆ Ļ░ÖņØ┤ ņäĖ Ļ░£ņØś ņä▒ļČäņ£╝ļĪ£ ļéśļłī ņłś ņ׳ļŗż.
ļ│æņ¦äņÜ┤ļÅÖņØä ĻĖ░ņżĆņ£╝ļĪ£ FSļŖö ņĀĢņĀü ņ£Āņ▓┤ ĒĢśņżæ(Hydrostatic force), FDļŖö ļÅÖņĀü ņ£Āņ▓┤ ĒĢśņżæ(Hydrodynamic force), FMļŖö Ļ│äļźśņäĀņŚÉ ņØśĒĢ£ ņןļĀź(Mooring line force)ņØä ņØśļ»ĖĒĢ£ļŗż. FMņØĆ ĒśäņłśņäĀ Ļ│äļźśļź╝ ņĀüņÜ®ĒĢśņśĆņ£╝ļ®░ Ļ│äļźśņäĀņŚÉ ņ×æņÜ®ĒĢśļŖö Ļ┤Ćņä▒ļĀźĻ│╝ ĒĢŁļĀźņŚÉ ņØśĒĢ£ ĒÜ©Ļ│╝ļŖö Ļ│ĀļĀżĒĢśņ¦Ć ņĢŖņĢśļŗż.
2.3 ļČĆņ£Āņ▓┤ņÖĆ Ļ│äļźś ņŗ£ņŖżĒģ£ņØś ņŚ░ņä▒ņĢīĻ│Āļ”¼ņ”ś
Fig. 1ņŚÉņä£ļŖö ņ×ģņé¼Ēīī, ļČĆņ£Āņ▓┤, Ļ│äļźś ņŗ£ņŖżĒģ£ Ļ░äņØś ņāüĻ┤ĆĻ┤ĆĻ│äņŚÉ ļö░ļźĖ ļ¬©ņŗØļÅäļź╝ ļéśĒāĆļéĖļŗż. ņ×ģņé¼ĒīīļŖö ņäĀĒśĢĻĘ£ņ╣ÖĒīīņØ┤Ļ│Ā, Ēīīļ×æņ£╝ļĪ£ ņĢ╝ĻĖ░ļÉ£ ļČĆņ£Āņ▓┤ņØś Ēæ£ļźśņÜ┤ļÅÖņ£╝ļĪ£ļČĆĒä░ ņ£äņ╣śņĀ£ņ¢┤ļź╝ ņ£äĒĢ┤ ĒśäņłśņäĀĒśĢĒā£ņØś Ļ│äļźś ņŗ£ņŖżĒģ£ņØä ņĀüņÜ®ĒĢśņśĆļŗż. ņ”ē, ņŗ£Ļ░ä ņśüņŚŁņŚÉņä£ Ēīīļ×æ ņżæ ļČĆņ£Āņ▓┤ņØś Ļ▒░ļÅÖņŚÉ ļīĆĒĢśņŚ¼ ĒÄśņ¢┤ļ”¼ļō£(Fairlead) ņóīĒæ£Ļ░Ć ĒśäņłśņäĀ Ļ│äļźś ņŗ£ņŖżĒģ£ ļØ╝ņØ┤ļĖīļ¤¼ļ”¼(Library)ņØś ņ×ģļĀźĻ░ÆņØ┤ ļÉśĻ│Ā ļČĆņ£Āņ▓┤ņØś Ēæ£ļźśņÜ┤ļÅÖ ņĀ£ņ¢┤ļź╝ ņ£äĒĢ£ Ļ│äļźśņäĀņØś ņןļĀźņØ┤ ĒśäņłśņäĀ Ļ│äļźś ņŗ£ņŖżĒģ£ ļØ╝ņØ┤ļĖīļ¤¼ļ”¼ņØś ņČ£ļĀźĻ░ÆņØ┤ ļÉśļŖö ņĢīĻ│Āļ”¼ņ”śņØ┤ļŗż.
Fig.┬Ā1
Coupled analysis diagram

Fig. 2ļŖö ņĀüņÜ®ļÉ£ ĒśäņłśņäĀ ļ░®ņĀĢņŗØņØś ĒśĢņāüņØä ļéśĒāĆļé┤ļ®░, ņŗØ(10), (11)Ļ│╝ Ļ░ÖņØ┤ ņĀĢņØśļÉ£ļŗż.
Fig.┬Ā2
Catenary shape
ņŚ¼ĻĖ░ņä£ lsļŖö Suspend length, x(ls), z(ls)ļŖö ĒĢ┤ņĀĆļ®┤Ļ╣īņ¦ĆņØś Ļ│äļźśņäĀ ĻĖĖņØ┤(Suspend length)ņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö ļģĖļō£(Node)ņØś xļ░®Ē¢źĻ│╝ zļ░®Ē¢źņØś ļ│Ćņ£ä, THņÖĆ TVļŖö ņłśĒÅē, ņłśņ¦ü ļ░®Ē¢źņØś ņןļĀź, wļŖö Ļ│äļźśņäĀņØś ļŗ©ņ£ä ĻĖĖņØ┤ ļŗ╣ ļ¼┤Ļ▓ī, KļŖö Ļ│äļźśņäĀņØś ņČĢļ░®Ē¢ź Ļ░Ģņä▒ņØä ņØśļ»ĖĒĢ£ļŗż. ļ¦ż ņŗ£Ļ░ä Ļ░äĻ▓® ļ¦łļŗż Ļ│äļźśņäĀņØś ĒĢ┤ņĀĆļ®┤ ņĀæņ┤ēņ¦ĆņĀÉ(Touchdown point)Ļ│╝ Suspend lengthļź╝ Ļ│äņé░ĒĢśĻ│Ā, ņØ┤ļĪ£ļČĆĒä░ ĒśäņłśņäĀ ļ░®ņĀĢņŗØņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņĀĢņĀü ĒÅēĒśĢņāüĒā£ņØś ĒśĢņāüĻ│╝ ĒÄśņ¢┤ļ”¼ļō£ņŚÉ ņ×æņÜ®ĒĢśļŖö ņןļĀźņØä Ļ│äņé░ĒĢ£ļŗż. ņŚ¼ĻĖ░ņä£, x, z ļ░®Ē¢źņØś ņĀĢņĀü ĒÅēĒśĢņāüĒā£ņØś ĒśĢņāü ļ░Å ņןļĀźņØä ļéśĒāĆļé┤ļŖö ņŗØ (10), (11)ņØä ļ¦īņĪ▒ņŗ£ĒéżĻĖ░ ņ£äĒĢ┤ ļ╣äņäĀĒśĢ ņłśņ╣śĒĢ┤ņäØ ļ░®ļ▓ĢņØĖ Newton-raphson & Jacobian ļ░®ļ▓ĢņØä ņØ┤ņÜ®ĒĢśņśĆļŗż. ņłśņ╣śĒĢ┤ņäØņØä ņ£äĒĢ£ Ļ│╝ņĀĢņØĆ ļŗżņØīĻ│╝ Ļ░ÖņØ┤ 3Ļ░Ćņ¦Ć ļŗ©Ļ│äļź╝ ļö░ļźĖļŗż.
Step. 1
ņŗØ (10), (11)ņØä Ļ░üĻ░ü fxŌĆ▓,z(╬▒n) ņØś ĒĢ©ņłśļĪ£ ņ×¼ļ░░ņŚ┤ĒĢ£ļŗż. xŌĆ▓ņØĆ Ļ│äļźśņäĀņØś ļĪ£ņ╗¼ ĒÅēļ®┤ņŚÉņä£ņØś ņłśĒÅē ļ░®Ē¢źņØś ņóīĒæ£ļź╝ ņØśļ»ĖĒĢśļ®░, zļŖö ņłśņŗ¼ ļ░®Ē¢źņØś ņóīĒæ£ļź╝ ņØśļ»ĖĒĢ£ļŗż.
Step. 2
Newton raphson & Jacobian ļ░®ļ▓ĢņØä ņØ┤ņÜ®ĒĢśņŚ¼ ļ¦ż ņŗ£Ļ░ä Ļ░äĻ▓® ļ¦łļŗż ļ│ĆĒÖöĒĢśļŖö ĒÄśņ¢┤ļ”¼ļō£ ņóīĒæ£ļĪ£ļČĆĒä░ Ļ│äļźśņäĀņØś ņןļĀźņØä Ļ│äņé░ĒĢśĻĖ░ ņ£äĒĢ£ ņłśņ╣śĒĢ┤ņäØņØä ņłśĒ¢ēĒĢ£ļŗż.
ļŗ©, ļ¦ż ĒāĆņ×äņŖżĒģØļ¦łļŗż ņןļĀźĻ│äņé░ņØä ņ£äĒĢ£ ļ░śļ│ĄĻ│äņé░ņØś ļ▓öņ£äļŖö

ņØ┤ļŗż.
Step. 3
ņóīĒæ£ļ│ĆĒÖś ļŗ©Ļ│äņØ┤ļŗż. ņĢ×ņä£ Ļ│äņé░ļÉ£
TH,
TVļŖö ĒÄśņ¢┤ļ”¼ļō£ņÖĆ ņĢĄņ╗żļ¦ü ņ¦ĆņĀÉņØ┤ ņØ┤ļŻ©ļŖö ļĪ£ņ╗¼ņóīĒæ£Ļ│äņŚÉņä£ņØś ņłśĒÅē, ņłśņ¦ü ļ░®Ē¢źņØś ņןļĀźņØä ņØśļ»ĖĒĢ£ļŗż.
Fig. 3ņØĆ
zļ░®Ē¢źņØä ņłśņŗ¼ ļ░®Ē¢ź ĻĖ░ņżĆņ£╝ļĪ£ Ļ│äļźśņäĀņØś
x-
y ĒÅēļ®┤ņØä ļéśĒāĆļé┤ļŖöļŹ░, ņĢĄņ╗żļ¦ü ņ¦ĆņĀÉņØ┤ Ļ│ĀņĀĢļÉ£ ĒÖśĻ▓ĮņŚÉņä£ ņØ╝ņ¦üņäĀņāü Ļ▒░ļ”¼Ļ░Ć ļÅÖņØ╝ĒĢ£ ņøÉņŻ╝ņŚÉņä£ņØś ĒÄśņ¢┤ļ”¼ļō£ ņןļĀźņØĆ Ļ░ÖļŗżļŖö ņøÉļ”¼ļź╝ ĒåĄĒĢ┤ ņĀäņŚŁņóīĒæ£Ļ│äļĪ£ ņóīĒæ£ļ│ĆĒÖśņØä ņłśĒ¢ēĒĢśņśĆļŗż.
Fig.┬Ā3
Fairlead & Anchoring point in local plane

2.4 ĒĢ┤ņäØņĢīĻ│Āļ”¼ņ”ś
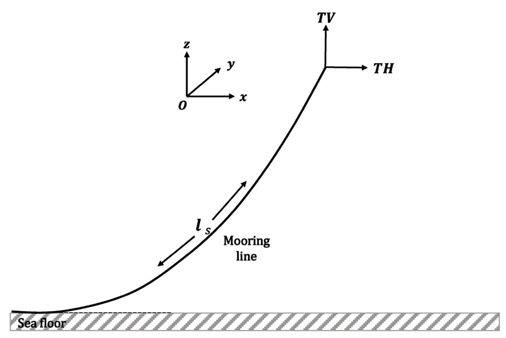
ņ£Āņ▓┤ņØś VOF ņØ┤ņåĪ ļ░®ņĀĢņŗØĻ│╝ ņ¦Ćļ░░ļ░®ņĀĢņŗØņØĆ ņ£ĀĒĢ£ ņ▓┤ņĀüļ▓Ģ(Finite Volume Method)ņŚÉ ņØśĒĢśņŚ¼ ņØ┤ņé░ĒÖö ļÉ£ļŗż. ņ¦Ćļ░░ļ░®ņĀĢņŗØ ņżæ ņŗ£Ļ░ä ĒĢŁņØĆ 1ņ░© ņĀĢĒÖĢļÅäņØś Euler scheme, Ļ│ĄĻ░ä ĒĢŁņØĆ 2ņ░© ņĀĢĒÖĢļÅäņØś Linear upwind schemeņØä ņé¼ņÜ®ĒĢśņśĆļŗż. ņåŹļÅäņÖĆ ņĢĢļĀźņØś ņŚ░ņä▒ņØä ņ£äĒĢ┤ņä£ SIMPLE ņĢīĻ│Āļ”¼ņ”śĻ│╝ PISO ņĢīĻ│Āļ”¼ņ”śņØä Ļ▓░ĒĢ®ĒĢ£ PIMPLE ņĢīĻ│Āļ”¼ņ”śņØä ņé¼ņÜ®ĒĢśņśĆļŗż. ņłśņ╣śĒĢ┤ņäØ Ļ│╝ņĀĢņØĆ
Fig. 4ņÖĆ Ļ░Öļŗż.
Fig.┬Ā4
Flowchart of solving algorithm
2.5 Ēīīļ×æņĪ░Ļ▒┤ņØś ņĀĢņØś
ĒĢ┤ņäØ ļÅäļ®öņØĖņØĆ 25
m(
L)Ō©ē 1
m(
B) Ō©ē 1
m(
D)ļĪ£ ļ¬©ļŹĖļ¦ü ĒĢśņśĆļŗż. Ēīīļ×æņØś ņłśņ╣ś ņśżņ░©ļź╝ Ļ│ĀļĀżĒĢśņŚ¼ ļīĆņāü ļČĆņ£Āņ▓┤ļŖö ņĪ░ĒīīĻ░Ć ņŗ£ņ×æļÉśļŖö Ļ▓ĮĻ│äļ®┤ņ£╝ļĪ£ļČĆĒä░ ĒĢ£ Ēīīņן ļ¢©ņ¢┤ņ¦ä Ļ││ņŚÉ ņ£äņ╣śĒĢśļ®░ ņ£ĀļÅÖņןņØś ņĢ×, ļÆż, ņ¢æņśåņØś Ļ▓ĮĻ│äļ®┤ņŚÉ ĒīīņØś Ļ░ÉņćĀ ņśüņŚŁņØä ņäżņĀĢĒĢśņŚ¼ ļ▓Įļ®┤ĒÜ©Ļ│╝ļź╝ ņĄ£ņåīĒÖöĒĢśļÅäļĪØ ņäżņĀĢĒĢśņśĆļŗż. ņ×ģņé¼Ēīī ņĪ░Ļ▒┤ņØĆ Ļ░£ļ░£ļÉ£ ĒöäļĪ£ĻĘĖļשņØś ļ╣äĻĄÉ ļ░Å Ļ▓Ćņ”ØņØä ņ£äĒĢ┤ ļ╣äņäĀĒśĢņä▒ņØä ņĄ£ņåīĒÖöĒĢśĻ│Āņ×É ĒĢśņśĆņ£╝ļ®░, ņØ┤ņŚÉ ļö░ļØ╝ ņ×ģņé¼ĒīīņØś ĒīīĻ▓Įņé¼Ļ░üņØä 3┬░ļ»Ėļ¦īņ£╝ļĪ£ ņäĀņĀĢĒĢśņśĆļŗż. ņ×ģņé¼ĒīīļŖö ņ¦äĒÅŁ, ļ░®Ē¢ź, ņŻ╝ĻĖ░ļŖö
Table 1Ļ│╝ Ļ░Öļŗż. ĒīīĻ│ĀļŖö 2cm, Ēīīļ░®Ē¢źņØĆ ņäĀņłśĒīī ļ░®Ē¢źņØ┤Ļ│Ā, ņŻ╝ĻĖ░ļŖö 1.0ņ┤łļČĆĒä░ 2.0ņ┤łĻ╣īņ¦Ć 0.2ņ┤ł Ļ░äĻ▓®ņ£╝ļĪ£ ņ┤Ø 6Ļ░Ćņ¦Ć ņĪ░Ļ▒┤ņ£╝ļĪ£ ņłśņ╣śĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśņśĆļŗż.
Table┬Ā1.
Regular wave condition

2.6 Ļ▓®ņ×Éļ»╝Ļ░ÉļÅä ĒĢ┤ņäØ
Ēīīļ×æņŚÉ ņØśĒĢ£ ļČĆņ£Āņ▓┤ ņÜ┤ļÅÖņØæļŗĄņØś ĒĢ┤ņäØņŚÉ ņĢ×ņä£ ĻĘ£ņ╣ÖĒīīņŚÉ ļīĆĒĢ£ Ļ▓®ņ×É ļ»╝Ļ░ÉļÅä ĒģīņŖżĒŖĖļź╝ ņłśĒ¢ēĒĢśņśĆļŗż.
Fig. 5ļŖö ņŻ╝ĻĖ░Ļ░Ć 1.0
sņØĖ ĒīīņŚÉ ļīĆĒĢ┤ ņ×Éņ£Āņłśļ®┤ņØä ĻĖ░ņżĆņ£╝ļĪ£ ņ×ģņé¼ ĒīīĻ│ĀņØś 2ļ░░ ņśüņŚŁ ļé┤ņŚÉņä£
z ļ░®Ē¢ź Ļ▓®ņ×É Ļ░£ņłśņŚÉ ļö░ļźĖ Ēīī ņ¦äĒÅŁņØś Ēü¼ĻĖ░ ļ╣äĻĄÉļź╝ ļéśĒāĆļé┤Ļ│Ā ņ׳ļŗż. Ļ▓®ņ×É Ļ░£ņłśņŚÉ ļö░ļźĖ Ēīī ņ¦äĒÅŁņØś ņłśņ╣śņśżņ░© ļ╣äĻĄÉļź╝ ņ£äĒĢ┤ Transient ĻĄ¼Ļ░äņØä ļ░░ņĀ£ĒĢśĻ│Ā Steady ĻĄ¼Ļ░äņŚÉņä£ 3ņŻ╝ĻĖ░ņØś Ēīī ņ¦äĒÅŁņØś ĒÅēĻĘĀĻ░ÆņØä
Fig. 6ņŚÉ ļéśĒāĆļé┤ņŚłļŗż.
Fig. 6ņØś
xņČĢņØĆ Ēīī ņ¦äĒÅŁ ļ░®Ē¢źņ£╝ļĪ£ņØś Ļ▓®ņ×É Ļ░£ņłśļź╝ ņØśļ»ĖĒĢśĻ│Ā,
yņČĢņØĆ Ļ│äņĖĪļÉ£ Ēīī ņ¦äĒÅŁņØä ņØśļ»ĖĒĢ£ļŗż.
Fig.┬Ā5
Comparison of wave amplitude
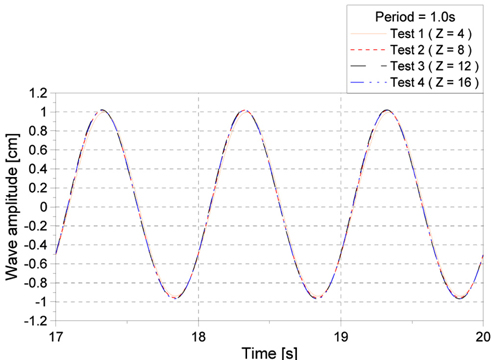
Fig. 6ņ£╝ļĪ£ļČĆĒä░ ņ×ģļĀźĒĢ£ Ēīī ņ¦äĒÅŁĻ│╝ Ļ│äņé░ļÉ£ Ēīī ņ¦äĒÅŁņØä ļ╣äĻĄÉĒĢ£ Ļ▓░Ļ│╝, Ļ▓®ņ×É Ēü¼ĻĖ░Ļ░Ć Ļ░Ćņן Ēü░ Test1ņŚÉņä£ļŖö ņĢĮ 4%ņØś ņśżņ░©Ļ░Ć ļ░£ņāØĒĢśņśĆĻ│Ā, Ļ▓®ņ×É Ēü¼ĻĖ░Ļ░Ć Ļ░Ćņן ņ×æņØĆ Test4ņŚÉņä£ļŖö ņĢĮ 0.5%ņśżņ░©Ļ░Ć ļ░£ņāØĒĢśņśĆļŗż. Ļ│äņé░ ņĀĢļÅäņÖĆ Ļ│äņé░ņŗ£Ļ░äņØś ĒĢ®ļ”¼ņĀüņØĖ ņĀłņČ®ņĢłņ£╝ļĪ£ņŹ© ņĢĮ 0.7%ņØś ņśżņ░©ļź╝ ļ│┤ņØ┤ļŖö Test3 Ļ▓®ņ×É Ēü¼ĻĖ░ļź╝ ņäĀņĀĢĒĢśņŚ¼ ņłśņ╣śĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśņśĆļŗż.
Fig. 7ņØĆ ņ£ĀļÅÖņןņØś Ļ▓®ņ×ÉļČäĒżļź╝ ļéśĒāĆļéĖļŗż. ņ×Éņ£Āņłśļ®┤ņØś ņĀĢļÅä ļåÆņØĆ Ļ│äņé░ņØä ņ£äĒĢ┤ ĒīīĻ░Ć ņ¦ĆļéśĻ░ĆļŖö ņśüņŚŁņŚÉ Ļ░Ćņן ņĪ░ļ░ĆĒĢ£ Ļ▓®ņ×Éļź╝ ņāØņä▒ĒĢśņśĆņ£╝ļ®░ ņĢ×ņä£ ņłśĒ¢ēĒĢ£ Ļ▓®ņ×É ņłśļĀ┤ļÅä ĒģīņŖżĒŖĖļź╝ ļ░öĒāĢņ£╝ļĪ£ ĒĢ£ ĒīīņןņØä ĻĖ░ņżĆņ£╝ļĪ£
xļ░®Ē¢ź ņĢĮ 130Ļ░£,
zļ░®Ē¢ź 12Ļ░£ņØś Ļ▓®ņ×Éļź╝ ņĀüņÜ®ĒĢśņśĆļŗż. ļśÉĒĢ£, ļČĆņ£Āņ▓┤ņØś ņÜ┤ļÅÖ ņØæļŗĄņØś ņĀĢļÅäļź╝ ļåÆņØ┤ĻĖ░ ņ£äĒĢ┤ ļČĆņ£Āņ▓┤ ņŻ╝ņ£äņŚÉ Ļ▓®ņ×É ņĪ░ļ░ĆļÅäļź╝ ņ”ØĻ░Ćņŗ£ņ╝░ļŗż. ņŗ£Ļ░äņśüņŚŁ Ļ│äņé░ņØä ņ£äĒĢ£ ņŗ£Ļ░äĻ░äĻ▓®ņØĆ T (ņŻ╝ĻĖ░)/200sņØ┤Ļ│Ā, ņ┤Ø ņé¼ņÜ®ļÉ£ Ļ▓®ņ×ÉņØś ņłśļŖö 1,300,000Ļ░£ņØ┤ļŗż.
Fig.┬Ā6
Mesh sensitivity test
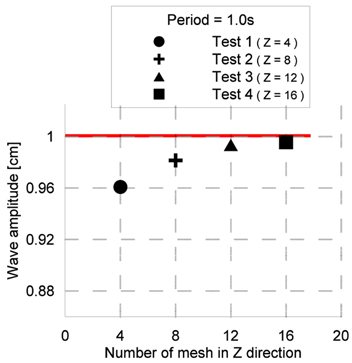
Fig.┬Ā7
Grid system

3. ĒżĒģÉņģ£ ĻĖ░ļ░śņØś ņŚ░ņä▒ĒĢ┤ņäØ
3.1 ļČĆņ£Āņ▓┤ ņÜ┤ļÅÖ
ļČĆņ£Āņ▓┤ņØś ņÜ┤ļÅÖņØĆ Ļ▓ĮĻ│äņÜöņåīļ▓Ģ(Boundary Element Method, BEM)ņØä ņØ┤ņÜ®ĒĢśļŖö ANSYS AQWAļź╝ ņé¼ņÜ®ĒĢśņŚ¼ Ļ│äņé░ĒĢśņśĆļŗż. ņØ┤ņāüņ£Āņ▓┤ļź╝ Ļ░ĆņĀĢĒĢ£ ņäĀĒśĢ ĒżĒģÉņģ£ ņØ┤ļĪĀņØä ĻĖ░ļ░śņ£╝ļĪ£ ļŗ©ņ£äņ¦äĒÅŁņØä Ļ░Ćņ¦ĆļŖö ņäĀĒśĢĒīīņŚÉ ļīĆĒĢ£ ļČĆņ£Āņ▓┤ņØś ņÜ┤ļÅÖ ņØæļŗĄ ļ░Å Ēīīļ×æ ĒĢśņżæņØä Ļ│äņé░ ĒĢśņśĆļŗż. ņŻ╝Ēīīņłś ņśüņŚŁņŚÉņä£ ļČĆĻ░Ćņ¦łļ¤ēĻ│äņłś(Added mass coefficient), ļ░®ņé¼Ļ░ÉņćĀĻ│äņłś(Radiation damping coefficient), Ēīīņ¦äĻĖ░ļĀź(Wave exciting force) ļō▒ņØä ņé░ņČ£ĒĢśĻ│Ā ņØ┤ļź╝ ĒåĄĒĢ┤ ņ×ģņé¼ĒīīņØś ņŻ╝ĒīīņłśņŚÉ ļīĆĒĢ£ ņÜ┤ļÅÖņØś Ēü¼ĻĖ░ļź╝ ļéśĒāĆļé┤ļŖö ņ¦äĒÅŁ ņØæļŗĄ ĒĢ©ņłś(Motion RAO)ļź╝ Ļ│äņé░ĒĢśņśĆļŗż.
3.2 ļČĆņ£Āņ▓┤ņÖĆ Ļ│äļźśņŗ£ņŖżĒģ£Ļ░äņØś ņŚ░ņä▒ĒĢ┤ņäØ
ņ£ĀĒĢ£ņÜöņåīļ▓Ģ(Finite Element Method, FEM)ņØä ņØ┤ņÜ®ĒĢśļŖö ņāüņÜ®ĒöäļĪ£ĻĘĖļשņØĖ Orcaflexļź╝ ĒåĄĒĢśņŚ¼ ļČĆņ£Āņ▓┤ņÖĆ Ļ│äļźś ņŗ£ņŖżĒģ£ Ļ░äņØś ņŗ£Ļ░ä ņśüņŚŁ ņŚ░ņä▒ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśņśĆļŗż. Orcaflexļź╝ ĒåĄĒĢ£ ņłśņ╣śĒĢ┤ņäØņØĆ ņĀäņ▓┤ Ļ│äļźśņäĀņØś ņäĖĻĘĖļ©╝ĒŖĖņŚÉ ļö░ļØ╝ ļģĖļō£ņĀÉĻ│╝ ņŖżĒöäļ¦üņØś Ļ░£ņłśĻ░Ć ņĀĢĒĢ┤ņ¦ĆĻ│Ā, ņØ┤ļź╝ ĒåĄĒĢ┤, Ļ░ü ļģĖļō£ņĀÉņŚÉ ņ¦łļ¤ēņØä ļČĆĻ│╝ĒĢśļŖö ņ¦æņżæņ¦łļ¤ēļ▓Ģ(Lumped mass)ņØä ĻĖ░ļ░śņ£╝ļĪ£ ĒĢ£ļŗż.
Fig. 8Ļ│╝ Ļ░ÖņØ┤ ņ┤Ø 4Ļ░£ņØś Ļ│äļźśņäĀņØ┤ ņäĀņłś ņäĀļ»ĖļĪ£ļČĆĒä░ ņóīĒśä, ņÜ░Ēśäņ£╝ļĪ£ Ē¢źĒĢśļÅäļĪØ Ļ│äļźśņäĀņØä ļ░░ņ╣śĒĢśņśĆĻ│Ā ĒÄśņ¢┤ļ”¼ļō£ņÖĆ ņĢĄņ╗żļ¦ü ņ¦ĆņĀÉņØś ņłśĒÅē ļ░®Ē¢ź Ļ▒░ļ”¼ņÖĆ ņłśņŗ¼ņØś ļ╣äļź╝ ņØśļ»ĖĒĢśļŖö Ļ│äļźśņäĀļ░śĻ▓Į(Foot print radius)ņØĆ 2ļ░░ļĪ£ ņäżĻ│äĒĢśņśĆļŗż.
Fig.┬Ā8
Layout of mooring lines
ļśÉĒĢ£, Ļ│äļźśņäĀņØś ņ¢æļĀź ļ░Å ĒĢŁļĀźĻ│äņłśļŖö Ļ░üĻ░ü 2.4, 1.5ļĪ£ Ļ│äņé░ĒĢśņśĆļŗż. ņØ┤ļŖö
DNVGL-OS-E301(2015)ņŚÉņä£ ņĀ£Ļ│ĄĒĢśļŖö Ļ░ÆņØä ĻĖ░ņżĆņ£╝ļĪ£ ņé░ņĀĢĒĢśņśĆļŗż.
4. Ļ▓░Ļ│╝ ļ╣äĻĄÉ
4.1 ņĀĢņĀüĒÅēĒśĢĻ│╝ ņ┤łĻĖ░ņןļĀź
Ēīīļ×æ ĒĢśņżæņØä ņĀüņÜ®ĒĢśĻĖ░ņŚÉ ņĢ×ņä£ ņĀĢņĀü ĒÅēĒśĢņāüĒā£(Static equilibrium state)ņŚÉņä£ Ļ│äļźśņäĀņØś ĒśĢņāü ļ░Å ĒÄśņ¢┤ļ”¼ļō£ņŚÉ ņ×æņÜ®ĒĢśļŖö ņןļĀźņØä ļ╣äĻĄÉĒĢśņśĆļŗż.
Fig. 9ļŖö ĒÄśņ¢┤ļ”¼ļō£ņŚÉņä£ ņĢĄņ╗żļ¦ü ņ¦ĆņĀÉĻ╣īņ¦Ć ņ┤Ø 50Ļ░£ņØś ņäĖĻĘĖļ©╝ĒŖĖļĪ£ ļéśļłł Ļ│äļźśņäĀņØś ĒśĢņāüņØä ļéśĒāĆļé┤Ļ│Ā ņ׳ļŗż. Ļ░£ļ░£ļÉ£ OpenFOAMĻ│╝ ņāüņÜ®ĒöäļĪ£ĻĘĖļשņØĖ Orcaflex Ļ░äņØś ņĀäņ▓┤ņĀüņØĖ ĒśĢņāüņØ┤ ņל ņØ╝ņ╣śĒĢ©ņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż.
Fig.┬Ā9
Equilibrium profile

Fig. 10ņØĆ ĒÄśņ¢┤ļ”¼ļō£ņŚÉ ņ×æņÜ®ĒĢśļŖö Ļ│äļźśņäĀņØś ņ┤łĻĖ░ņןļĀźņØä ļ╣äĻĄÉĒĢ£ ĻĘĖļ”╝ņØ┤ļŗż. Line1, Line3ņØĆ ņäĀņłś, ņäĀļ»ĖņØś ļīĆĻ░üņäĀ ļ░®Ē¢źņŚÉ ņ£äņ╣śĒĢ£ Ļ│äļźśņäĀņØä ļéśĒāĆļéĖļŗż. ĒśäņłśņäĀ ļ░®ņĀĢņŗØņ£╝ļĪ£ļČĆĒä░ Ļ│äņé░ļÉ£ OpenFOAM Ļ│äļźś ņŗ£ņŖżĒģ£ņØś ņ┤łĻĖ░ņןļĀźņØĆ OrcaflexņØś Ļ▓░Ļ│╝ņÖĆ ņל ņØ╝ņ╣śĒĢśļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż.
Fig.┬Ā10
Initial tension at fairlead

4.2 ļČĆņ£Āņ▓┤ņØś Ļ▒░ļÅÖĻ│╝ Ļ│äļźśņןļĀź
ņ×ģņé¼ĒīīņØś Ļ░üļÅäĻ░Ć 0┬░(ņäĀņłśĒīī)ņØĖ ņĪ░Ļ▒┤ņŚÉņä£ ņ×ģņé¼Ēīī ņŻ╝ĻĖ░ņŚÉ ļö░ļźĖ ļČĆņ£Āņ▓┤ ņÜ┤ļÅÖ ņØæļŗĄ ĒŖ╣ņä▒ ļ░Å Ļ│äļźśņäĀņØś ņןļĀźļ│ĆĒÖöņŚÉ ļīĆĒĢ£ ļ╣äĻĄÉļź╝ ņłśĒ¢ēĒĢśņśĆļŗż(
Davidson and Ringwood, 2017).
Fig. 11ņØĆ ņŻ╝ĻĖ░Ļ░Ć 1.6sņØĖ ņĪ░Ļ▒┤ņŚÉņä£ OpenFOAM, OrcaflexļĪ£ļČĆĒä░ Ļ│äņé░ļÉ£ ļČĆņ£Āņ▓┤ņØś ņÜ┤ļÅÖ ņØæļŗĄņŚÉ ļīĆĒĢ£ ņŗ£Ļ│äņŚ┤ņØä ļéśĒāĆļéĖļŗż. ņĀĢļ¤ēņĀü ļ╣äĻĄÉļź╝ ņ£äĒĢ┤ ļæÉ ņłśņ╣śĒĢ┤ņäØ Ļ░äņØś ņ£äņāü(Phase)ņØä ļ¦×ņČöņ¢┤ ļ╣äĻĄÉĒĢśņśĆļŗż. HeaveņÖĆ PitchņØś Ļ▓ĮņÜ░ ļæÉ Ļ░£ņØś ņŗ£ĻĘĖļäÉņØ┤ ņĀĢļ¤ēņĀüņ£╝ļĪ£ ņל ņØ╝ņ╣śĒĢśļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. Surge ņØæļŗĄņŚÉņä£ļŖö ņĀĢļ¤ēņĀüņ£╝ļĪ£ ņØ╝ļČĆ ņāüņØ┤ĒĢ£ Ļ▓░Ļ│╝Ļ░Ć ļéśĒāĆļéśņ¦Ćļ¦ī, Ļ░£ļ░£ļÉ£ Ļ│äļźśļ¬©ļōł ņĮöļō£ļŖö OrcaflexņØś Ļ▓░Ļ│╝ņÖĆ ņĀĢļ¤ēņĀüņ£╝ļĪ£ ņ£Āņé¼ĒĢ£ Ļ▓░Ļ│╝ļź╝ ļ│┤ņŚ¼ņŻ╝ļŖö Ļ▓āņØä ĒÖĢņØĖĒĢśņśĆļŗż. ļśÉĒĢ£, Surge ņØæļŗĄņŚÉņä£ ļČĆņ£Āņ▓┤ņÖĆ Ļ│äļźśņŗ£ņŖżĒģ£ Ļ░äņØś ņŚ░ņä▒ ņÜ┤ļÅÖņ£╝ļĪ£ ļČĆĒä░ ĻĖ░ņØĖĒĢśļŖö ĒĢśļ¬©ļŗē(Harmonic) ĒśäņāüņØ┤ Ļ┤ĆņĖĪļÉśĻ│Ā ņ׳ļŖöļŹ░, ņØ┤ļź╝ ĒĢ┤ņäØĒĢśĻ│Āņ×É Ļ░üĻ░üņØś ņŗ£Ļ░äņØ┤ļĀźņØä ĒīīņøīņŖżĒÄÖĒŖĖļ¤╝ņ£╝ļĪ£
Fig. 12ņŚÉ ļéśĒāĆļé┤ņŚłļŗż.
Fig.┬Ā11
Time history of motion response (period = 1.6s)
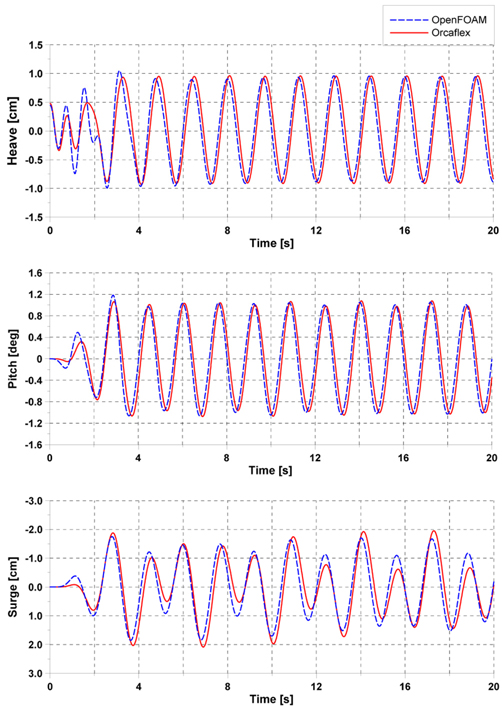
Fig. 12ļŖö ņ×ģņé¼ĒīīņØś ņŻ╝ĻĖ░ņŚÉ ļö░ļźĖ Surge ņÜ┤ļÅÖņØś ĒīīņøīņŖżĒÄÖĒŖĖļ¤╝ņØä ļéśĒāĆļéĖļŗż. ņŖżĒÄÖĒŖĖļ¤╝ļ¦łļŗż 2Ļ░£ņØś Ēö╝Ēü¼Ļ░Ć ĒÖĢņŚ░Ē׳ ĻĄ¼ļČäļÉśņ¢┤ Ļ┤Ćņ░░ļÉśļŖöļŹ░ ņāüļīĆņĀüņ£╝ļĪ£ Ļ│ĀņŻ╝ĒīīņłśņŚÉ ņ£äņ╣śĒĢ£ Ēö╝Ēü¼ļŖö ņ×ģņé¼ĒīīņØś ņŻ╝Ēīīņłśļź╝ ņØśļ»ĖĒĢśĻ│Ā ņĀĆņŻ╝ĒīīņłśņØĖ 2.2rad/sņŚÉ ņ£äņ╣śĒĢśļŖö Ēö╝Ēü¼ļŖö Ļ│äļźśņŗ£ņŖżĒģ£ņØś Ļ│Āņ£Āņ¦äļÅÖņłśņÖĆ ņØ╝ņ╣śĒĢśļŖö ņØæļŗĄņØä ņØśļ»ĖĒĢ£ļŗż. OpenFOAMĻ│╝ OrcaflexņØś Ļ▓░Ļ│╝ļōż Ļ░äņŚÉ ņ¦äĒÅŁņØś ņ░©ņØ┤ļŖö ņĪ┤ņ×¼ĒĢśņ¦Ćļ¦ī Ļ░üĻ░üņØś Ēīī ņŻ╝ĒīīņłśņÖĆ Ļ│äļźśņŗ£ņŖżĒģ£ņØś Ļ│Āņ£Āņ¦äļÅÖņłśņŚÉ ņØśĒĢ£ Ēö╝Ēü¼ņ£äņ╣śļŖö ņĀĢĒÖĢĒ׳ ņśłņāüĒĢśļŖö Ļ▓░Ļ│╝ņÖĆ ņØ╝ņ╣śĒĢśļŖö Ļ▓āņØä ĒÖĢņØĖ ĒĢĀ ņłś ņ׳ļŗż.
Fig.┬Ā12
Surge response spectrum
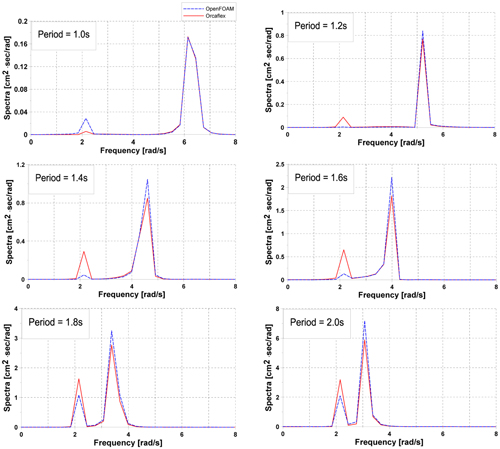
Fig. 13,
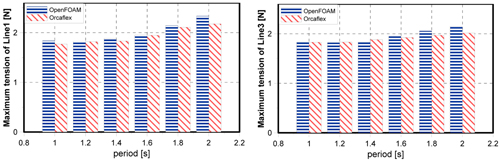
14ļŖö Ļ│äļźśņäĀņØś ņןļĀźņŚÉ ļīĆĒĢ┤ ĒÅēĻĘĀĻ░ÆĻ│╝ ņĄ£ļīĆĻ░ÆņØä ļéśĒāĆļé┤ņŚłļŗż. ņןļĀźņØś ĒÅēĻĘĀĻ░ÆņØĆ ļæÉ ļ░®ļ▓Ģ Ļ░äņŚÉ Ēü░ ņ░©ņØ┤ļź╝ ļ│┤ņØ┤ņ¦Ć ņĢŖņĢśņ£╝ļéś ņןļĀźņØś ņĄ£ļīĆĻ░ÆņØĆ ĒŖ╣ņĀĢ ĒīīņŻ╝ĻĖ░ņŚÉņä£ ņĢĮĻ░äņØś ņ░©ņØ┤ļź╝ ļ│┤ņØ┤Ļ│Ā ņ׳ļŖöļŹ░, ņØ┤ļŖö Ļ░£ļ░£ļÉ£ Ļ│äļźśņŗ£ņŖżĒģ£ņÜ® ļ¬©ļōłņØ┤ ĒśäņłśņäĀļ░®ņĀĢņŗØņØä ņé¼ņÜ®ĒĢ©ņ£╝ļĪ£ņŹ© ĒÅēļ®┤ļé┤ņØś ņÜ┤ļÅÖļ¦ī Ēæ£ĒśäņØ┤ Ļ░ĆļŖźĒĢśĻ│Ā, ļÅÖņŚŁĒĢÖņĀüņØĖ Ļ│äļźśņäĀņØś Ļ▒░ļÅÖņØä Ēæ£ĒśäĒĢśļŖöļŹ░ ĒĢ£Ļ│äĻ░Ć ņ׳ņ¢┤ņä£ ņāØĻĖ░ļŖö Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż. ņØ┤ļŖö ņČöĒøä ļ¬©ĒśĢņŗżĒŚśņØä ĒåĄĒĢ┤ ņČöĻ░ĆņĀüņØĖ ļ╣äĻĄÉļź╝ ņłśĒ¢ēĒĢśĻ▒░ļéś, ņŚ░ņä▒ļ¬©ļōłņØś ĒśäņłśņäĀļ░®ņĀĢņŗØņØä ņ¦æņżæņ¦łļ¤ēļ▓Ģņ£╝ļĪ£ Ļ░£ļ¤ēĒĢśļŖö ļ░®ļ▓ĢņØä ĒåĄĒĢ┤ Ļ▓Ćņ”ØņØ┤ ņØ┤ļŻ©ņ¢┤ņ¦ł ņśłņĀĢņØ┤ļŗż.
Fig.┬Ā13
Mean tension at fairlead
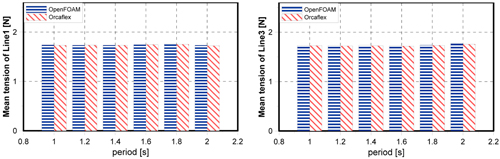
Fig.┬Ā14
Maximum tension at fairlead
5. Ļ▓░ ļĪĀ
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņśżĒöłņåīņŖż CFD ĒöäļĪ£ĻĘĖļשņØĖ OpenFOAMļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ļČĆņ£Āņ▓┤ņÖĆ Ļ│äļźś ņŗ£ņŖżĒģ£Ļ░äņØś ņ¢æļ░®Ē¢ź ņŚ░ņä▒ ļ¬©ļōłņØä Ļ░£ļ░£ĒĢśĻ│Ā ņØ┤ļź╝ ņāüņÜ®ĒöäļĪ£ĻĘĖļשņØś ņłśņ╣śĒĢ┤ņäØĻ▓░Ļ│╝ņÖĆ ļ╣äĻĄÉĒĢśņŚ¼ Ļ▓Ćņ”ØĒĢśņśĆļŗż. ņĀĢņĀüĒÅēĒśĢ ņāüĒā£ņŚÉņä£ Ļ│äļźśņäĀņØś ĒśĢņāü ļ░Å ņ┤łĻĖ░ņןļĀźņØä ļ╣äĻĄÉĒ¢łņ£╝ļ®░, ņäĀņłśĒīī ņĪ░Ļ▒┤ņØś ĻĘ£ņ╣ÖĒīī ņĪ░Ļ▒┤ņŚÉņä£ ļČĆņ£Āņ▓┤ņØś Ļ▒░ļÅÖ ļ░Å ĒÄśņ¢┤ļ”¼ļō£ ņ¦ĆņĀÉņØś ņןļĀźņØä ņŻ╝Ēīīņłś ņśüņŚŁņŚÉņä£ņØś ņŖżĒÄÖĒŖĖļ¤╝ ļ░Å ņŗ£Ļ░äņśüņŚŁņŚÉņä£ņØś ņĄ£ļīĆĻ░ÆĻ│╝ ĒÅēĻĘĀĻ░ÆņØä ĒåĄĒĢ┤ ņĀĢļ¤ēņĀüņ£╝ļĪ£ ĒÅēĻ░ĆĒĢśņśĆļŗż. ļ│Ė ņŚ░ĻĄ¼ļĪ£ļČĆĒä░ ļŗżņØīĻ│╝ Ļ░ÖņØĆ Ļ▓░ļĪĀņØä ņ¢╗ņØä ņłś ņ׳ļŗż.
(1) Ļ░£ļ░£ļÉ£ OpenFOAM ņĮöļō£ņØś Heave, Pitch ņÜ┤ļÅÖņØĆ ņāüņÜ®ĒöäļĪ£ĻĘĖļשņØĖ OrcaflexĻ░äņŚÉ ņĀĢļ¤ēņĀüņ£╝ļĪ£ ņל ņØ╝ņ╣śĒĢśļŖö Ļ▓āņØä ĒÖĢņØĖĒĢśņśĆļŗż.
(2) Ļ░£ļ░£ļÉ£ OpenFOAM ņĮöļō£ņØś Surge ņÜ┤ļÅÖ ļ░Å Ļ│äļźśņäĀņØś ņןļĀźņØĆ ņāüņÜ®ĒöäļĪ£ĻĘĖļשņØĖ OrcaflexņÖĆ ņĀĢļ¤ēņĀüņ£╝ļĪ£ ĒŚłņÜ® ļ▓öņ£ä ļé┤ņØś ņ░©ņØ┤ļź╝ ļ│┤ņØ┤ļ®░ Ļ░ÖņØĆ Ļ▓ĮĒ¢źņØä ļ│┤ņ×äņØä ĒÖĢņØĖĒĢśņśĆļŗż.
(3) ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö ņĀÉņä▒ĒÜ©Ļ│╝ļź╝ Ļ│ĀļĀżĒĢśļŖö CFDļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ļČĆņ£Āņ▓┤ņÖĆ Ļ│äļźś ņŗ£ņŖżĒģ£Ļ░äņØś ņŚ░ņä▒ ņÜ┤ļÅÖņØä ĻĄ¼ĒśäĒĢśņśĆļŗż. ņČöĒøä ļ¬©ĒśĢņŗżĒŚś ļśÉļŖö ņŚ░ņä▒ļ¬©ļōłņØś Ļ░£ņäĀņØä ĒåĄĒĢ┤ ņČöĻ░ĆņĀüņØĖ ļ╣äĻĄÉ ļ░Å Ļ▓Ćņ”ØņØ┤ ĒĢäņÜöĒĢśļ®░, ļŹö ļéśņĢäĻ░Ć ņØ┤ļź╝ ļ░öĒāĢņ£╝ļĪ£ ĻĘ╣ĒĢ£ ĒÖśĻ▓Į ņĪ░Ļ▒┤Ļ│╝ Ļ│äļźśņäĀņØś ļÅÖņĀü ĒÜ©Ļ│╝ļź╝ Ļ│ĀļĀżĒĢ£ ņŚ░ĻĄ¼Ļ░Ć ņÜöĻĄ¼ļÉ£ļŗż.
NOTES
It is noted that this paper is revised edition based on proceedings of KAOST 2017 in Busan.
Ļ░Éņé¼ņØś ĻĖĆ
ļ│Ė ņŚ░ĻĄ¼ļŖö ņé░ņŚģĒåĄņé░ņ×ÉņøÉļČĆ ņé░ņŚģĻĖ░ņłĀĒśüņŗĀņé¼ņŚģ (Ļ│╝ņĀ£ļ▓łĒśĖ: 10063405) ŌĆ£ņ£äņ╣śņ£Āņ¦ĆņÖĆ Ļ│äļźś ņŗ£ņŖżĒģ£ņØä ņĀüņÜ®ĒĢśņŚ¼ ARC7 ņĪ░Ļ▒┤ņŚÉņä£ ņŚ░ņżæņÜ┤ņÜ®ņØ┤ Ļ░ĆļŖźĒĢ£ ļČüĻĘ╣ĒĢ┤ ĻĖ░ļ░ś ļČĆņ£ĀņŗØ ĒĢ┤ņ¢æĻĄ¼ņĪ░ļ¼╝ ĒśĢņāü Ļ░£ļ░£ŌĆØĻ│╝ņĀ£ņØś ņ¦ĆņøÉņ£╝ļĪ£ ņłśĒ¢ēļÉśņŚłņØīņØä ļ░ØĒ×Öļŗłļŗż.
References
Davidson, J., Ringwood, J. V.. (Mathematical Modelling of Mooring Systems for Wave Energy Converters-A Review, Energies, 2017). 10(5):666 10.3390/en10050666.

DNVGL Position Mooring DNV GL AS, 2015). DNVGL-OS-E301.
Hong, S.Y., Lee, P.M., Kim, Y.C., Hong, D.C.. (An Experimental Analysis on the Motion Response of a Moored Semi-Submersible Platform in Regular Waves, Journal of Ocean Engineering and Technology, 1988). 2(1):59-70.
Ok, H. T., Lee, S. J., Choi, J. H.. (Numerical simulation of motion of single and side-by-side vessels in regular waves using OpenFOAM, Ships and Offshore Structures, 2017). 12(6):793-803 10.1080/17445302.2016.1265697.

Sirnivas, S., Yu, Y. H., Hall, M., Bosma, B.. (Coupled mooring analyses for the wec-sim wave energy converter design tool ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering American Society of Mechanical Engineers; 2016). V006T09A023.
Wu, G., Kim, J. W., Jang, H., Baquet, A.. (CFD-Based Numerical Wave Basin for Global Performance Analysis OMAE2016 2016.
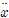 ņÖĆ
ņÖĆ 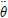 ļŖö ļČĆņ£Āņ▓┤ņØś ļ│æņ¦ä, ĒÜīņĀä ļ░®Ē¢źņØś Ļ░ĆņåŹļÅä ņä▒ļČä ļ│ĆĒÖöļ¤ēņØä ļéśĒāĆļéĖļŗż. xCG , ╬ĖCGļŖö Ļ░üĻ░ü ļČĆņ£Āņ▓┤ņØś ļ│æņ¦ä ņÜ┤ļÅÖĻ│╝ ĒÜīņĀäņÜ┤ļÅÖ ļ│Ćņ£äļź╝ ļéśĒāĆļé┤ļ®░ FCG ņÖĆ MCGļŖö Ļ░üĻ░ü ļČĆņ£Āņ▓┤ņØś ļ¼┤Ļ▓ī ņżæņŗ¼ņŚÉ ņ×æņÜ®ĒĢśļŖö ļ│æņ¦ä ņÜ┤ļÅÖĻ│╝ ĒÜīņĀäņÜ┤ļÅÖņØś ĒלĻ│╝ ļ¬©ļ®śĒŖĖļź╝ ļéśĒāĆļéĖļŗż. ņŚ¼ĻĖ░ņä£ FCGņÖĆ MCGļŖö ņŗØ (8), (9)ņÖĆ Ļ░ÖņØ┤ ņäĖ Ļ░£ņØś ņä▒ļČäņ£╝ļĪ£ ļéśļłī ņłś ņ׳ļŗż.
ļŖö ļČĆņ£Āņ▓┤ņØś ļ│æņ¦ä, ĒÜīņĀä ļ░®Ē¢źņØś Ļ░ĆņåŹļÅä ņä▒ļČä ļ│ĆĒÖöļ¤ēņØä ļéśĒāĆļéĖļŗż. xCG , ╬ĖCGļŖö Ļ░üĻ░ü ļČĆņ£Āņ▓┤ņØś ļ│æņ¦ä ņÜ┤ļÅÖĻ│╝ ĒÜīņĀäņÜ┤ļÅÖ ļ│Ćņ£äļź╝ ļéśĒāĆļé┤ļ®░ FCG ņÖĆ MCGļŖö Ļ░üĻ░ü ļČĆņ£Āņ▓┤ņØś ļ¼┤Ļ▓ī ņżæņŗ¼ņŚÉ ņ×æņÜ®ĒĢśļŖö ļ│æņ¦ä ņÜ┤ļÅÖĻ│╝ ĒÜīņĀäņÜ┤ļÅÖņØś ĒלĻ│╝ ļ¬©ļ®śĒŖĖļź╝ ļéśĒāĆļéĖļŗż. ņŚ¼ĻĖ░ņä£ FCGņÖĆ MCGļŖö ņŗØ (8), (9)ņÖĆ Ļ░ÖņØ┤ ņäĖ Ļ░£ņØś ņä▒ļČäņ£╝ļĪ£ ļéśļłī ņłś ņ׳ļŗż. ņØ┤ļŗż.
ņØ┤ļŗż.