|
 |
- Search
| J. Ocean Eng. Technol. > Volume 33(6); 2019 > Article |
|
Abstract
The ice keel gouge and seabed interaction is one of the major considerations in the design of an Arctic pipeline system. Ice keel and seabed interaction engineering models based on experimental data, which give an explicit equation for estimating the ice gouging depth, have been suggested. The suggested equations usually overestimate the ice keel gouging depth. In addition, various types of numerical analyses have been carried out to verify the suggested engineering model equations in comparison to the experimental data. However, most of numerical analysis results were also overestimated compared with the laboratory experimental data. In this study, a numerical analysis considering the contact condition and geostatic stress was carried out to predict the ice keel gouging depth and compared with the previous studies. Considering the previously mentioned conditions, more accurate results were produced compared with the laboratory experiment results and the error rate was reduced compared to previous numerical analysis studies.
일반적인 해저 파이프라인과는 달리 극지 파이프라인을 안전하게 운용하기 위해 특별하게 고려되어야할 문제는 수심이 얕은 빙해역에서 흔히 발생하는 빙쇄굴(Ice gouge) 현상이다.
빙쇄굴(Ice gouge)현상은 외해에서 해류(Current)와 바람(Wind)에 의해 초기 속도를 갖는 거대한 Ice keel(경사 빙)이 얕은 수심으로 이동하면서 해저면을 긁는 북극해의 해안가에서 볼 수 있는 가장 두드러진 특징 중 하나이다. 이러한 빙쇄굴 현상은 해저에 매설된 파이프라인이나 케이블에 직접적인 손상을 일으키거나, 해저지반으로 전달되는 빙하중으로부터 토질의 간접적인 변형에 의해서도 파괴가 발생하게 된다(Woodworth-Lynas et al., 1996).
빙쇄굴 발생 시 얼음은 외해에서 갖는 초기 운동에너지가 토질의 저항 에너지와 평형을 이룰때까지 해저면을 긁게 되는데 쇄굴거리는 최대 수 km에 달하고 쇄굴깊이가 수 m에 달하는 것으로 관측되고 있다(Truskov and Surkov., 1991). 따라서 극지해양 파이프라인은 빙쇄굴에 노출되지 않을 정도로 깊게 매설해야 한다. 하지만 매설깊이의 증가는 비용 증가의 문제를 초래하기 때문에 빙쇄굴에 의한 해저면 쇄굴깊이의 정확한 산정이 요구된다. 이러한 빙쇄굴 메커니즘에 대한 연구는 다양한 형태로 이루어져왔고, 일반적으로 실내실험이나 관측자료를 기본으로 하여 이론식의 제시 및 수치해석적 방법으로 비교하여 결과를 확인하려는 방법이 시도되어 왔다.
먼저 최근의 빙쇄굴 모델과 관련된 국내 연구로 Choi and Lee (2002)는 기존의 빙쇄굴 모델 해석결과를 비교하여 기존 모델의 적용한계를 분석하고, 수면하부에 경사각(Keel angle)을 갖는 새로운 모델을 제시하여, 비교적 간단한 실험과 비교하는 연구를 수행하였다. 또한 국외 연구로는 원심모형실험을 실시하고 이에 따른 빙쇄굴 깊이를 예측하는 PRISE(Pressure ridge ice scour experiment)모델 식들을 개발하여 제안하였으며(Woodworth-Lynas et al., 1996), 이를 기초로 하여 최근 Sand로 조성된 지반에서의 영향을 비교하는 실내모형실험 연구(Arnau and Ivanović, 2019)를 비롯하여 다양한 형태의 FEM(Finite element method)을 이용한 비교 및 검증 연구가 수행되어지고 있다. 빙쇄굴과 같은 대변형 해석은 기존의 FEM해석으로는 한계가 있으며, Lagrangian과 Eulerian을 결합한 새로운 FEM의 해석기법이 적용되어왔고 그 예로 Arbitrary Lagrangian-Eulerian(ALE)을 이용한 비교연구(Konuk et al., 2005) 및 Coupled Eulerian-Lagrangian (CEL)기법을 이용한 비교연구(Abdalla et al., 2009)가 각각 수행되어 보고되고 있으며, ALE 및 CEL기법의 수치해석적 빙쇄굴 연구에 대한 상세한 비교 분석 또한 수행되고 있다(Babaei and Sudom., 2014).
DNV(Det Norske veritas)는 2010년에 종료된 Ice pipe joint industry project(JIP)에서 Ice-soil-pipeline의 상호작용의 수치 해석적 모델링 및 분석에 대한 지침을 개발하였고, 이를 바탕으로 CEL기법을 이용한 Ice-soil-pipeline 상호작용에 대한 연구를 수행하였다(Banneyake et al., 2011). 하지만 현재까지의 수치해석으로는 복잡한 형상을 가진 실제얼음 형상과 다양한 빙쇄굴 환경변수를 모두 고려하지 못하는 실정이다.
따라서 본 연구에서는 현재까지 발표된 여러 빙쇄굴 연구 중 원심모형실험 및 PRISE모델 식, 그리고 이를 수치해석적으로 비교한 연구를 함께 분석 하여 빙쇄굴 메커니즘에 대한 이해를 도모하고, 이를 바탕으로 기존의 연구에서 반영되지 않았던 해저지반의 Geostatic stress 및 해저지반 상호작용 즉 Ice keel과 해저지반의 마찰에 대한 영향을 고려한 새로운 해석을 실시하여, 본 해석 기법의 정확성에 대해 검증하고자 한다.
기존의 빙쇄굴 연구는 원심모형실험에 의한 PRISE모델 식을 바탕으로 FEM을 이용한 다양한 비교 연구가 수행되어 왔으며, 본 연구에서 비교 분석 하고자 하는 PRISE모델 식은 u(0, 0, 0)으로 표현되며 이는 수평방향의 빙쇄굴에 의한 변위를 나타내고, 식 (1)과 같다(Woodworth-Lynas et al., 1996).
여기서, z는 쇄굴 아래 깊이, B는 쇄굴 폭, D는 쇄굴 깊이이며, 해당 논문의 해석은 RRISE모델 05-D1, 06-D1 case에 해당한다.
원심모형실험 및 PRISE모델 식 (1)과 비교를 위한 FEM해석은 ALE 해석기법을 이용한 수치해석이 먼저 수행되었으며(Konuk et al., 2005), 이를 바탕으로 최근에는 CEL해석 기법을 적용하여 빙쇄굴 수치해석을 보다 현실적으로 모사할 수 있도록 발전해왔다(Abdalla et al., 2009). 이러한 수치해석을 이용한 비교 연구는 PRISE모델 식과 비교되고 나아가 매설된 파이프라인을 고려하여 빙쇄굴에 의한 파이프라인의 변형을 분석하는 수준으로 발전해왔다(Banneyake et al., 2011). Fig. 1은 기존의 연구들이 고려한 빙쇄굴 메커니즘을 보여주고 있다. 기존의 연구들은 Fig. 1에서와 같이 일정한 Attack angle(α)이 적용된 형상의 Ice keel이 해저지반 상부에서의 깊이 DOG(Depth of gouge)에서 일정한 속도로 출발하여 멈추거나 수직 방향의 운동은 없이 단지 지정된 속도로 계속 끌려나가는 형태의 연구를 수행하였다. 이를 토대로 빙쇄굴 해석의 초기 정보인 DOG 및 Ice keel의 속도(Attack velocity) 및 각도(Attack angle) 등 다양한 해석조건을 적용하여, Ice keel 하부에서부터 해저지반의 깊이에 따라 끌리는 수평방향의 변위를 추적하여 각각 비교 하였다.
그러나 원심모형실험과 비교된 기존의 수치해석(ALE, CEL기법)은 얼음과 토질사이의 마찰에 의한 영향은 고려하지 않고 시뮬레이션 하였으며, 이는 빙쇄굴에 의한 정면과 측면부에 쇄굴되며 쌓이는 토질저항력을 고려하지 않은 결과이다. 이처럼 기존의 수치해석 연구는 다양한 빙쇄굴 환경변수를 모두 고려하지 않고, 빙쇄굴 현상에서 영향이 다소 큰 환경변수만 고려한 단순화된 수치해석 결과임을 알 수 있다.
본 연구의 목적은 기존의 수치해석을 이용한 연구들에서 고려하지 않은 흙의 마찰에 의한 영향을 고려하여 보다 정확한 Ice keel에 의한 해저지반의 빙쇄굴 해석을 실시하는 것으로, 이를 위해 기존의 연구와 본 연구에 반영될 해석 모델간의 적합성 검증을 Geostatic stress 조건을 추가 적용하여 아래와 같이 실시하였다. 기존의 수치해석에 적용된 CEL기법은 격자 왜곡 및 Contact문제를 해결하는데 장점이 있어 FEM을 이용한 토목 및 기초공학 분야의 수치해석에 다양하게 활용되어지고 있다. 본 연구에서도 FEM을 이용한 기존의 빙쇄굴 수치해석 연구들과 같이 범용유한요소해석 프로그램인 Abdalla(2009)의 연구를 바탕으로 경계조건 및 해석 설정을 구현 하였다.
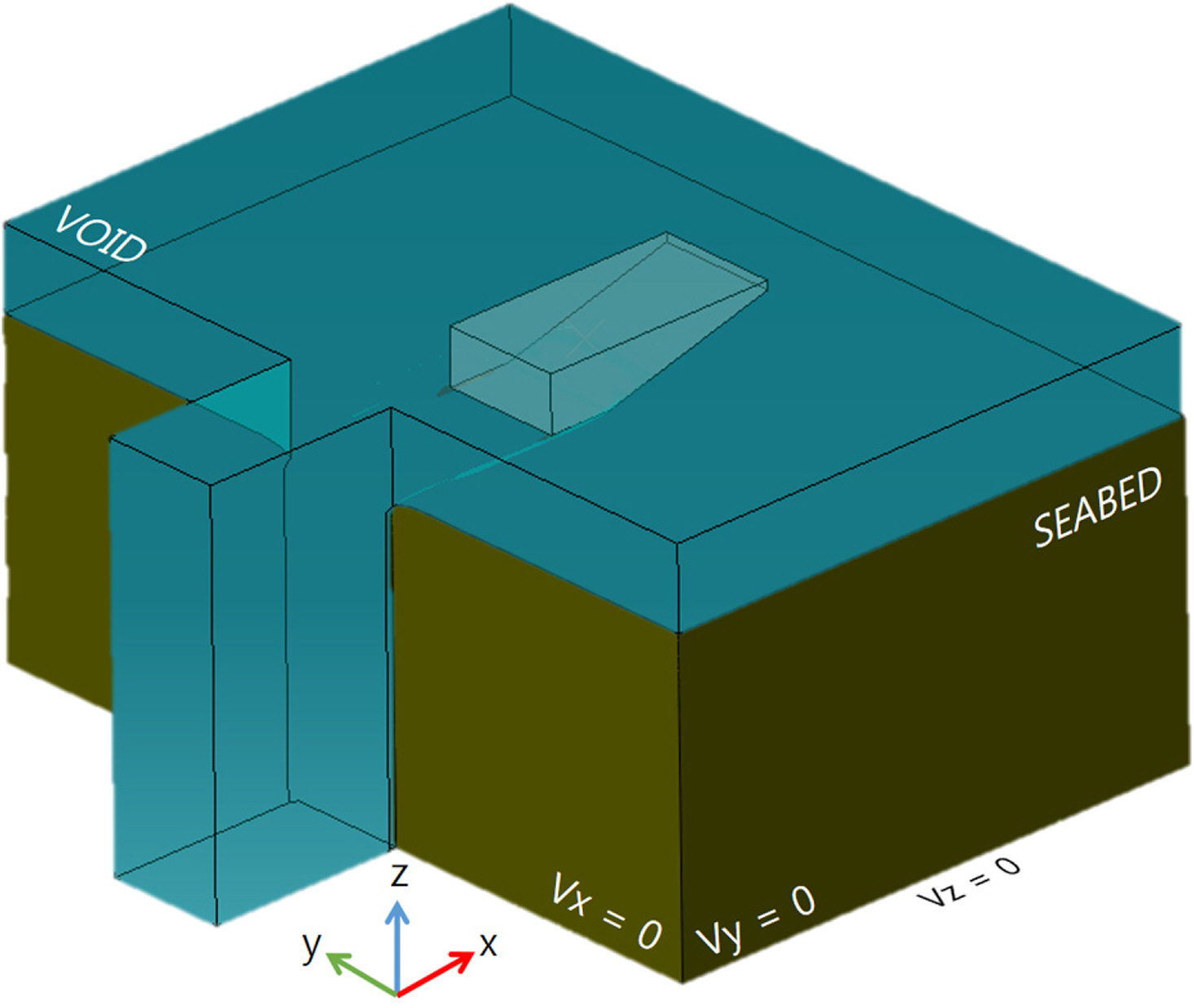
해석 모델링은 Fig. 2와 같이 Eulerian 도메인 내부에 Lagrangian 부분을 포함하여 모델링 한 후, 초기 위치에 Volume fraction tool을 이용하여, VOID라고 명시되어있는 부분을 제외한 나머지를 Eulerian 격자(Mesh)로 생성 하였다. 이와같이 생성된 Eulerian mesh의 위치에 해저지반에 해당하는 물성치를 부여해줌으로써 해저지반을 조성 하였다. 또한 Ice keel의 경우 Eulerian 도메인 내부에 위치하지만 Eulerian 격자로 생성하지 않고 Lagrangian 모델로 형성 후 강체(Rigid body)로 가정하여 모델링 하였다.
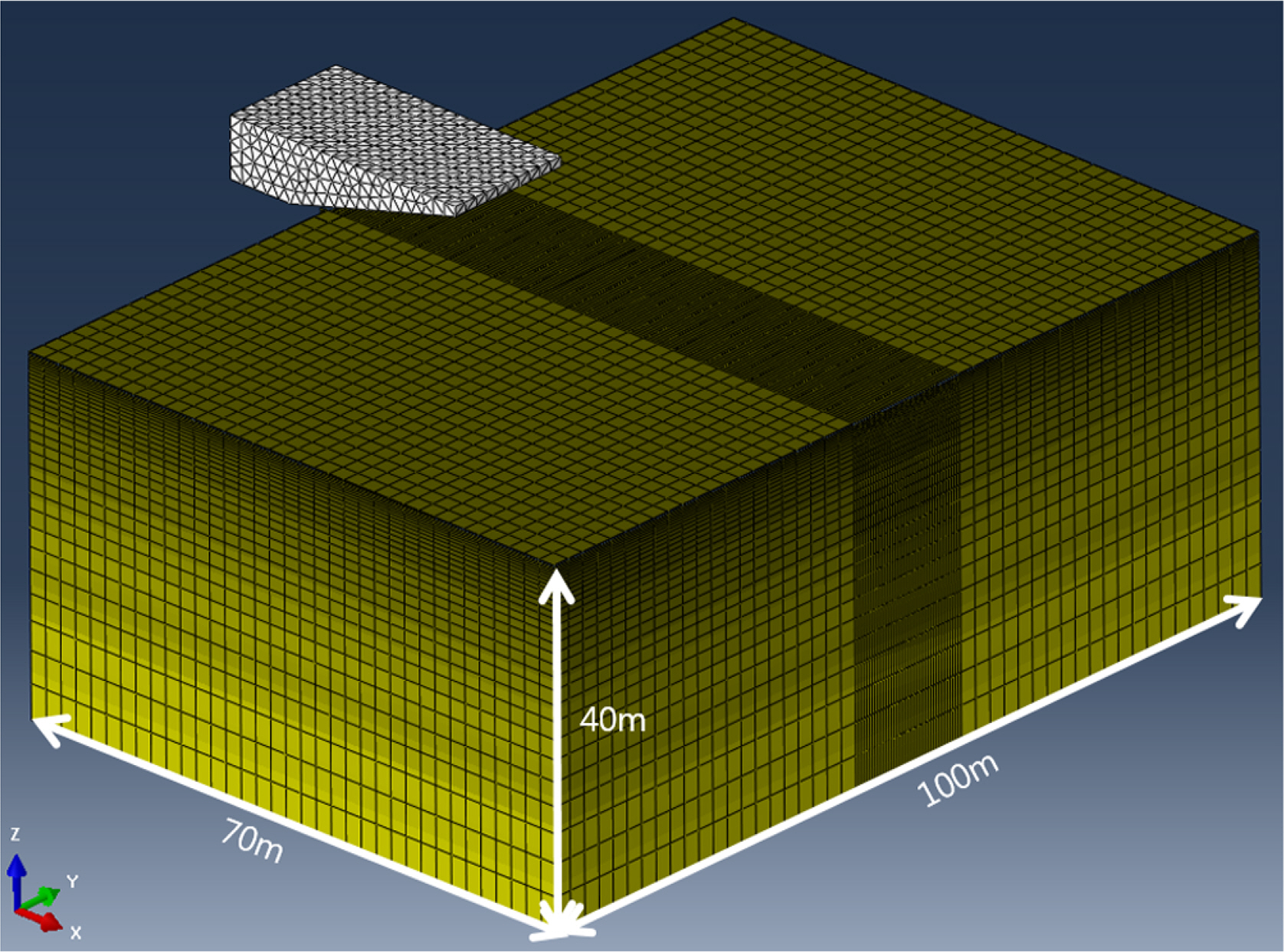
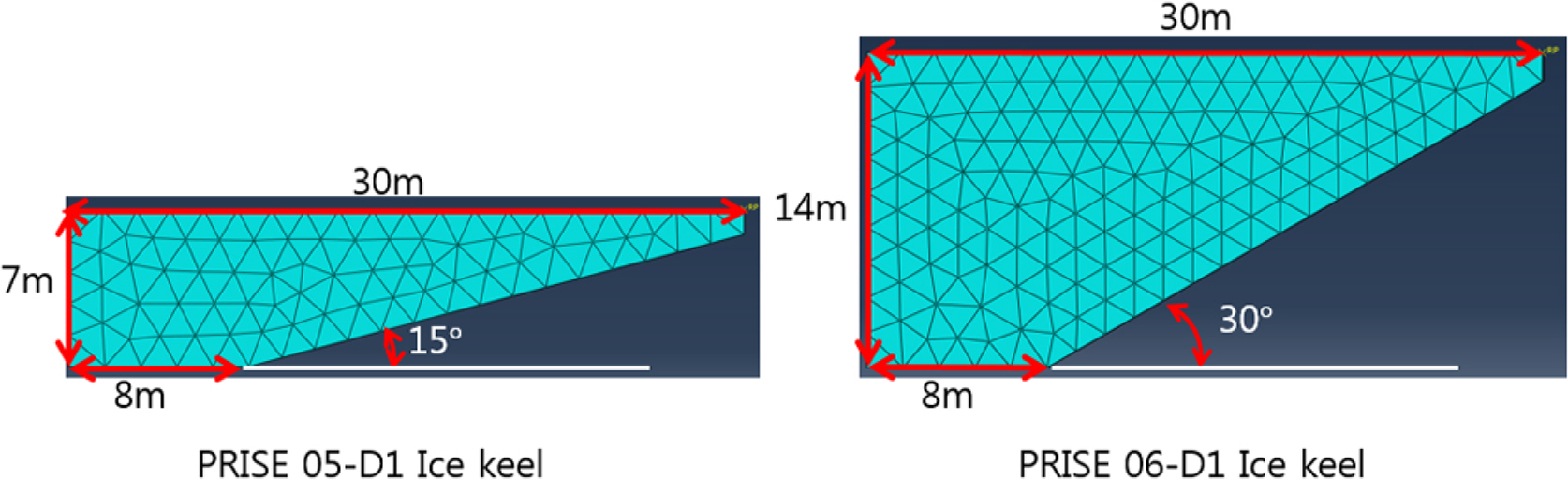
경계조건(Boundary condition)은 해저지반 각 면의 수직방향 변위를 고정해주는 조건을 부여하였고, Ice keel 또한 기존 연구들과 동일한 조건으로 수평방향 즉 축을 제외한 모든 변위를 구속하는 조건을 부여하였다. ‘VOID’부분을 제외한 전체 해석모델링을 Fig. 3에 나타내었다. 기존의 연구들과 비교를 위해 원심모형실험 Case들 중 DOG 1m, Keel width 15m, Attack angle 15°, 30°인 2가지 조건(PRISE 05-D1, 06-D1 case)을 선정하였다(Woodworth-Lynas et al., 1996). 설정된 두가지 Case는 Table 1에 나타내었고, 기존의 연구와 동일하게 Ice keel의 형상을 설정하였으며 각 Case에 따른 Ice keel의 형상 및 치수를 Fig. 4에 나타내었다.
또한 기존의 수치해석 연구는 해저지반에 부여되는 물성치(Material property)를 von-Mises 항복조건을 적용한 점토(Clay)로 조성하였으나, 본 연구에서는 보다 토질의 거동 모사를 잘 구현하기 위해 점토로 조성되는 해저지반 토질의 점착력 및 마찰각을 고려하는 Mohr-Coulomb 항복조건을 적용하였다. 적용되는 해저지반의 물성치는 원심모형실험(Woodworth-Lynas et al., 1996)에서 적용된 지반물성을 반영하였고, 이를 Table 2에 나타내었다.
기존 연구와 비교를 위해 빙쇄굴에 의해 발생되는 해저지반 깊이에 따른 변위 추정은 고정된 Eulerian domain 내부에 Ice keel이 지나가는 위치에 해당하는 해저지반 노드번호(Node number)를 각각 지정하여 추출하였다. 이는 ABAQUS의 Tracer particle 기능을 이용하였으며, PRISE 05-D1 Case에 Tracer particle이 적용된 형상을 Fig. 5에 나타내었다.
해석의 순서는 초기 Eulerian domain 내부에 해저지반을 생성하여 물성치를 부여하고 각각의 면에 경계조건을 기존 수치해석과 동일하게 설정하였다. 그러나 기존의 연구는 해저지반을 단일지반(One layer soil)으로 가정하여 자중(Gravity)만을 적용하였으나, 본 연구에서는 Geostatic stress 조건을 추가 적용하였다. 여기서 Geostatic stress 조건이란 기존에 부여된 지반 물성치와 수면 아래 해저지반의 In-situ 조건을 반영하기 위해 해저지반 깊이별 응력을 적용함으로써(ABAQUS, 2018), Natural field condition과 보다 유사하게 조성할 수 있는 기법으로, 이는 마지막 해석 Step까지 적용하였다. 이와같은 Geostatic stress는 ABAQUS에서 흙의 전응력(Total stress)으로 적용되며 식 (2)와 같다.
여기서, σv는 전응력이며, σ'v는 유효응력(Effective stress)이고, u는 간극수압(Pore pressure), γsat는 흙의 포화단위중량(Saturated unit weight of soil), z는 깊이이다. 또한 해저지반의 보다 효과적인 모델링을 위해 포화도(Saturation)와 간극비(Void ratio)를 설정하여 부여하였고, 기존의 연구와 동일하게 Ice keel이 일정한 속도(0.1m/s)로 x축 방향(수평방향)으로만 움직이도록 속도를 적용하였다.
본 연구는 기존 연구(원심모형실험, PRISE모델 식, 수치해석)의 Case와 동일한 해석조건을 부여하였고, 기존의 수치해석 연구에서 고려하지 않은 해저지반을 보다 현실적 모델링하기 위한 Mohr-Coulomb 항복조건 및 Geostatic stress를 추가 적용하였다. 본 해석의 결과는 Ice keel의 하단 부를 기준으로 해저지반의 깊이 별 수평방향 변위를 산정하여 PRISE모델 식 및 원심모형실험 결과(Woodworth-Lynas et al., 1996), 그리고 Abdalla의 수치해석적 연구결과와 각각 비교하였다.
Abdalla의 연구는 해저지반 변위를 측정하는 거리 즉, Ice keel이 해저지반에 쇄굴이 시작되는 출발점(Starting point)에서부터(Fig. 4 참조) 정확히 몇 m의 거리에서 Ice keel 아래 해저지반 변위(Horizontal subgouge displacement)가 측정되었는지 정확한 거리가 명시되어 있지 않다. 그러나 PRISE 05-D1 case의 해석결과에 의하면 Ice keel의 출발점으로부터 거리에 따라 빙쇄굴에 의한 Ice keel 하부 해저지반 변위는 점차 증가하는 것으로 나타났다. 따라서 출발점으로부터 해저지반 변위가 관측되는 거리는 기존 연구들과 비교 시 매우 중요한 요소이다. 따라서 본 연구에서는 Woodworth-Lynas et al.(1996)의 원심 모형실험에서 해저지반 변위가 측정되는 지점인 전체 해저지반으로 조성된 가운데 지점을 기준으로 약 10m거리에서 Ice keel을 DOG 1m로 설정 후 출발함을 감안하여, 본 연구의 비교 및 분석되는 모든 결과는 출발점으로부터 10m 거리의 해저지반 변위로 선정하였다.
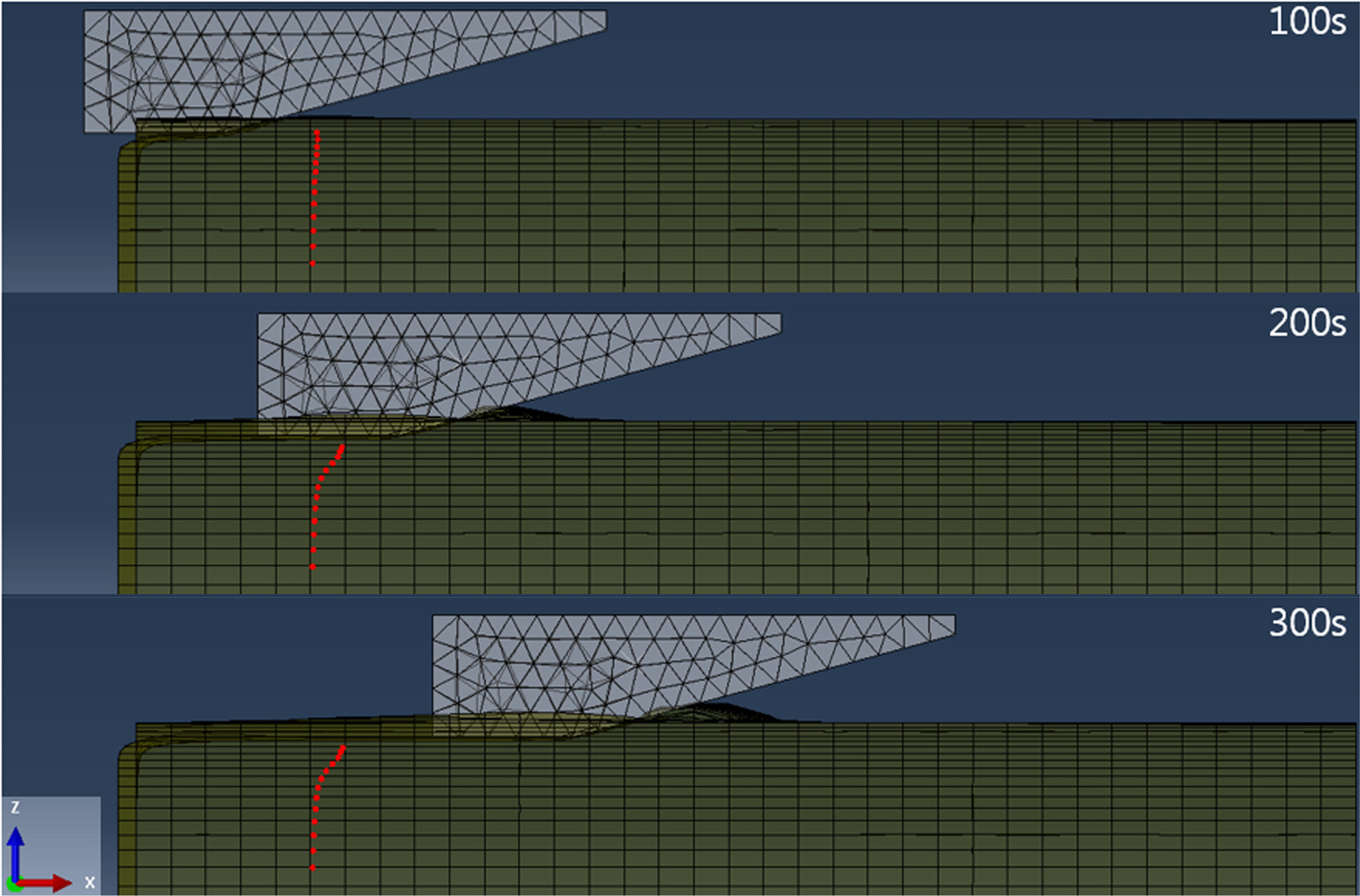
출발점으로부터 거리 10m에서의 생성된 Tracer particle의 변위가 발생하는 100s, 200s, 300s에서의 PRISE 05-D1의 Case 형상을 Fig. 6에 나타내었다. Ice keel의 속도가 0.1m/s로 설정됨에 따라 시간이 100s가 지난 후에도 이동거리가 작게 나타나므로 해석시간을 350s로 설정하여 Ice keel의 이동거리를 늘려 지정된 Tracer particle의 변위가 일정해지도록, 즉 더 이상의 변위가 발생하지 않도록 충분한 해석시간을 주어 해저지반의 변위 결과를 관측하였다.
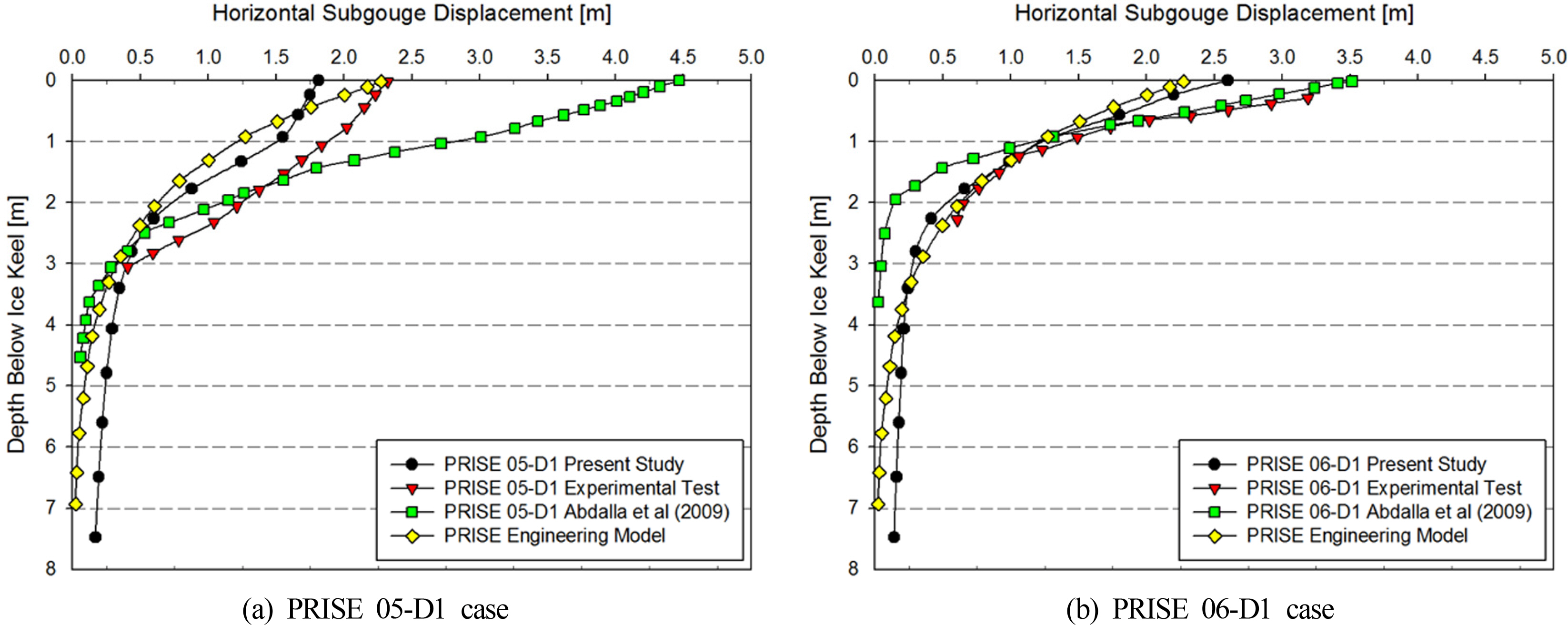
이와 같이 지정된 Tracer particle을 추적함으로써 Ice keel 아래 해저지반 변위를 측정하였으며, 기존 연구의 원심모형실험, PRISE모델 식 및 수치해석과의 비교 결과를 Fig. 7에 나타내었다. Fig. 7에서 PRISE모델 식 결과인 05-D1(Fig. 7(a)), 06-D1(Fig. 7(b))는 동일한 결과이며, 이는 Attack angle이 고려되지 않았기 때문이다. Fig. 8은 원심모형실험을 기준으로 하여, 본 연구 결과(Non-contact case)와 PRISE모델 식 그리고 기존의 수치해석결과를 각각 Ice keel 아래 0m 지점과 최대오차율이 발생하는 지점 그리고 1m 단위로 오차율을 측정한 평균 오차율을 비교하여 4절의 Table 4-5의 Present study의 Non-contact case로 정리하여 나타내었다.
결과를 보면 PRISE 05-D1 case에서 원심모형실험과 본 연구 비교 시 Ice keel 아래 2m지점에서 약 21%로 최대 오차율(Maximum error rate)이 발생하였고, 기존의 수치해석 연구와 PRISE 모델 식의 최대 오차율은 각각 38%, 29%로 본 연구의 오차율 보다 크게 나타났다. 또한 원심모형실험과 본 연구의 평균 오차율(Average error rate)은 15%로 나타났고, 기존의 수치해석 연구와 PRISE모델 식은 각각 32%, 18%의 오차율로 본 연구의 해석 결과보다 더 큰 오차가 발생되는 것으로 나타났다. 하지만 Ice keel 아래 0m지점에서의 오차율은 PRISE모델 식이 원심모형실험 결과와 가장 일치하는 결과를 보였다.
PRISE 06-D1 case 결과의 경우 원심모형실험과 본 연구 비교 시 Ice keel 아래 0.5m지점에서 25%로 최대 오차율이 발생하였고, 기존의 수치해석 연구와 PRISE 모델 식의 최대 오차율은 각각 약 22%, 24%로 본 연구의 오차율과 거의 비슷하게 나타났다. 그러나 원심모형실험과 본 연구의 평균 오차율은 14%로 나타났고, 기존의 수치해석 연구와 PRISE모델 식은 각각 16%, 15%의 오차율로 본 연구의 해석 결과보다 더 큰 오차가 발생되는 것으로 나타났다. 하지만 PRISE 06-D1(Fig. 7(b))의 경우 원심모형실험에서 Ice keel 아래 0m 지점의 결과가 제시되지 않고 0.38m의 결과만을 제시하고 있으므로 본 연구도 최상단 위치인 0.38m 결과를 산출하여 비교 하였다. 그 결과 본 연구의 오차율은 22%이며 기존의 수치해석 연구는 6.1%로 원심모형실험 결과와 가장 일치하였다.
이러한 오차 발생원인은 기존의 수치해석 연구는 본 연구와 동일한 CEL기법을 사용하였으나, 해저지반의 내부 응력 즉 Geostatic stress를 고려하지 않은 차이점으로 판단된다.
Ice keel이 해저지반을 긁으며 지나가는 빙쇄굴 현상에서 쇄굴이 진행되면서 Ice keel의 측면 및 하단부에서 발생되는 토질저항력과 전면에 쌓이는 토질이 크게 증가하기 때문에 해저지반과 얼음과의 마찰의 고려는 해석에 있어서 중요한 변수이다. 앞 절의 본 연구결과가 기존의 수치해석에 비해 원심모형실험 결과와 비교 시 대체적으로 더 근접한 결과를 도출했음에도 여전히 원심모형실험과의 다소 큰 오차율은 존재하였다. 이는 기존의 수치해석적 연구가 해저지반과 Ice keel의 상호작용을 제대로 구현해내지 못했음을 유추할 수 있다. 따라서 Ice keel과 해저지반의 상호작용을 보다 정확하게 구현해내기 위해서 마찰에 의한 영향이 고려되어야 한다.
이와 같이 Ice keel과 해저지반의 마찰에 의한 영향을 고려한 빙쇄굴 수치해석을 위해 먼저 모델링 및 경계조건은 앞선 3절에서 실시된 해석 조건과 동일하게 설정하였다. 또한 기존 연구에서 반영되지 않은 해저지반의 마찰에 의한 영향을 고려하기 위해 Abaqus/Explicit의 Contact조건을 적용하였다. 여기서 해석에 적용되는 Contact 조건의 대표적인 Shear friction 모델 중 가장 널리 사용되는 Coulomb friction 모델을 적용하였다(ABAQUS, 2018).
이와 같은 Coulomb friction 모델은 본 해석에 사용된 상용 유한요소 해석 프로그램인 ABAQUS에서 Equivalent frictional stress(τeq)와 Critical stress(τcrit)로 정의되며 이는 식 (4)-(5)와 같다(ABAQUS, 2018).
여기서, τ1, τ2는 접촉면에서의 전단응력(Shear stresses)이고, μ는 마찰계수이며, p는 접촉압력(Contact pressure)이다. 이러한 Contact 조건은 ABAQUS에서 Penalty constraint을 시행하는 ‘hard’ contact 조건에서 규정되고, 접촉 후 분리가 허용된 Penalty algorithm을 사용하여 Ice keel과 해저지반 사이의 마찰을 설정하여 적용하였다.
또한 Ice keel과 지반의 마찰계수는 실험에 의해 산정된 기존의 연구(Barker and Timco, 2003)를 바탕으로 설정하였다(Table 3). 하지만 해당연구 결과는 Sand(사질토)에서 측정된 결과로 본 연구에서는 Clay로 지반을 조성한 점을 감안하여, Sand보다는 마찰에 의한 영향이 적을 것으로 판단된다. 통상적으로 Steel과 Sand의 마찰계수를 0.3, Steel과 Clay의 마찰계수를 0.2가 제안되어(Grigoriev and Meilikhov, 1997; NAVFAC, 1982) 적용되고 있다. 또한 해당연구(Anne and Garry, 2003)에서 염빙(Saline ice)의 마찰계수를 0.03으로 제안한바, 본 연구에서는 Ice keel과 해저지반의 마찰계수를 언급된 연구들을 참고하여 0.05로 설정하였다.
본 절의 연구결과는 기존의 수치해석 연구에서 고려되지 않았던, 해저지반을 단일지반이 아닌 해저지반 내 Geostatic stress를 적용할 뿐 아니라 Ice keel과 해저지반의 마찰이 고려된 조건으로 설정하여 원심모형실험 결과와 오차율을 줄이고, 수치해석의 정확성을 높이기 위함에 목적이 있다.
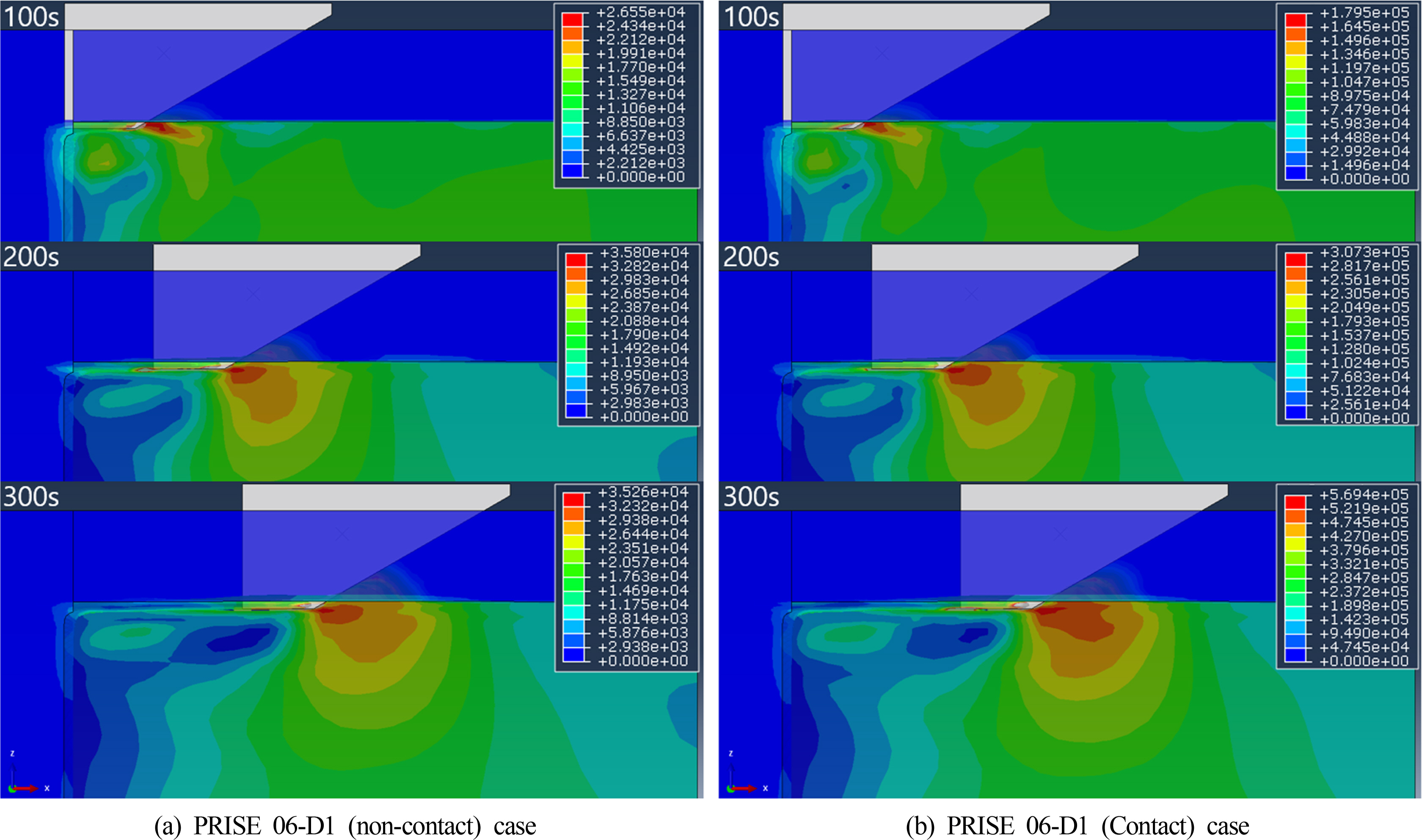
먼저 Fig. 8는 마찰에 의한 영향이 고려되지 않은(Fig. 8(a)) 3절의 결과와 마찰에 의한 영향을 고려한(Fig. 8(b)) 해저지반의 von-Mises 응력 차이를 PRISE 06-D1 case로 보여주고 있다. 결과를 보면 기존에 안정화 되어있던 지반이 Ice keel과 부딪혀 쇄굴되는 형상을 확인 할 수 있다. Ice keel 전면에 쌓이는 토질의 양은 쇄굴거리가 증가함에 따라 더 커지며 전면에 쌓이는 토질이 증가될수록 해저지반 아래에서 발생되는 응력 또한 서서히 증가되었다. 여기서 Contact조건 즉 마찰이 고려된 Fig. 8(b)에서 더 큰 응력이 발생되는 것을 알 수 있다. 실제로 마찰을 고려하지 않은 결과인 Fig. 8(a)와 약 10배 정도의 응력차이를 보였다.
Fig. 9는 마찰에 의한 영향을 고려한 Ice keel 아래 해저지반 변위를 기존 연구들과 비교한 결과를 보여준다. 결과를 보면 기존의 마찰을 고려하지 않은 결과보다 원심모형실험 결과와 잘 일치하는 것을 알 수 있다. 또한 기존 연구들과 본 연구에서 실시된 해석결과를 각각 원심모형실험 결과를 기준한 오차율로 정리하여 Table 4-5의 Present study의 Contact case로 나타내었다.
결과를 보면 RRISE 05-D1 case에서 원심모형실험과 본 연구 비교 시 Ice keel 아래 2.5m지점에서 4.6%로 최대 오차율이 발생하였고, Ice keel 아래 0m지점에서는 오차율은 0.82%, 전체 결과의 평균 오차율은 2.7%로 원심모형실험 결과와 매우 근접한 결과를 보였다.
또한 PRISE 06-D1 case의 경우 원심모형실험과 본 연구 결과 비교 시 Ice keel 아래 0.38m에서 5.1%로 최대 오차율이 발생되었고, 전체 결과의 평균 오차율은 3.9%로 나타났다.
정리된 결과에서 기존의 수치해석 연구, PRISE모델 식, 그리고 마찰을 고려하지 않은 3절(Non-contact)의 결과 보다, 본 4절에서 실시된 해저지반 Geostatic stress 및 마찰에 의한 영향을 고려한 수치해석이 Ice keel과 해저지반의 상호작용을 보다 현실적이고 원심모형실험 결과와 보다 더 근접한 결과를 도출해 내는 것을 확인하였다.
본 연구는 기존의 빙쇄굴 연구들 가운데 원심모형실험, PRISE모델 식, 수치해석 연구에 대한 비교 연구로 첫째로, 기존의 수치해석에 적용되지 않았던 해저지반 내 Geostatic stress적용하여 이전 연구들과 비교하였다. 둘째로, Ice keel과 해저지지반의 마찰을 고려한 새로운 수치해석을 실시하여 이전 연구들과의 오차율을 분석하였으며, 결과는 다음과 같이 요약할 수 있다.
(1) 기존의 빙쇄굴 연구들 중 원심모형실험에 근거한 PRISE모델 식(Woodworth-Lynas et al., 1996)중 05-D1, 06-D1의 2가지 case를 선정하였다. 또한 이를 수치 해석적으로 접근한 연구(Abdalla et al., 2009)의 가능성에 대해 알아보았다.
(2) 기존의 수치해석 연구를 바탕으로 CEL 기법을 적용한 유한요소모델링을 실시하여 원심모형실험 환경과 동일한 환경을 모사하였으며, 단일지반으로 고려된 기존의 수치해석 연구와 달리 Geostatic stress를 고려한 해석을 실시하여 비교하였다. 그 결과 원심모형실험 결과와 비교 시 기존의 수치해석 연구보다 오차율은 줄었으나, 여전히 다소 큰 오차율이 발생되는 것을 알 수 있었다.
(3) 이러한 오차율을 줄이고, Ice keel과 해저지반의 상호작용을 보다 더 실제 현상에 근접하게 적용하기 위해 Ice keel과 해저지반의 마찰의 영향을 추가하여 새로운 수치해석을 실시하였다. 그 결과 마찰에 의한 영향을 고려하지 않은 연구보다 원심모형실험 결과와 더 잘 일치하였으며, 오차율도 현저히 감소하는 결과를 보였다.
추후 Ice keel의 수직방향 운동과 흙의 저항에 의한 빙속 감속등을 고려한 빙쇄굴 수치해석을 실시하여 해저지반 변위를 분석하고, 이를 바탕으로 극지 파이프라인의 안전한 매설심도에 관한 연구를 진행해 나갈 예정이다.
후기
본 연구는 2019년 산업통상자원부 지원 산업핵심기술과제 ‘ARC7 극지환경용 해양플랜트 내빙구조 설계기술 개발(10063417)’ 과제와 2019년 한국해양대학교 부산 산학융합지구조성사업단산학협력 R&D(N0001629)과제의 지원으로 수행된 결과임.
Fig. 9
Comparison of horizontal subgouge deformations with previous studies considering contact condition

Table 1
Gouge event of PRISE model test
| Test NO. | Soil state | Gouge event | Attack angle | Depth of gouge | Keel width |
|---|---|---|---|---|---|
| PRISE 05 | Clay | D-1 | 15° | 1m | 15m |
| PRISE 06 | Clay | D-1 | 30° | 1m | 15m |
Table 2
Material properties of clay
| γsat [kg/m3] | Friction angle Φ [°] | Cohesion c [kPa] | |
|---|---|---|---|
| Soft clay | 1611 | 0.01 | 12 |
Table 3
Friction coefficients from laboratory studies
| Sand [Bulldozing] | Sand [Transition] | Sand [Sliding] | Saline ice | |
|---|---|---|---|---|
| Ice velocity [0.1 m/s] | 0.40 | 0.32 | 0.23 | 0.03 |
Table 4
Comparison of error rate with experimental result (PRISE 05-D1)
| Present study | PRISE engineering model | Analysis by Abdalla et al.(2009) | ||
|---|---|---|---|---|
| Non-contact | Contact | |||
| 0 m error rate | 19 % | 0.82 % | 0.78 % | 38 % |
| Position of Maximum error rate | 21 % | 4.6 % | 29 % | 38 % |
| Average error rate | 15 % | 2.7 % | 18 % | 32 % |
Table 5
Comparison of error rate with experimental result (PRISE 06-D1)
| Present study | PRISE engineering model | Analysis by Abdalla et al.(2009) | ||
|---|---|---|---|---|
| Non-contact | Contact | |||
| 0 m error rate | 22 % | 5.1 % | 24 % | 6.1 % |
| Position of maximum error rate | 25 % | 5.1 % | 24 % | 22 % |
| Average error rate | 14 % | 3.9 % | 15 % | 16 % |
References
ABAQUS. (2018). ABAQUS User’s Manual. ABAQUS 2018, Rhode Island. Dssault Systems.
Abdalla, B., Pike, K., Eltaher, A., Jukes, P., & Duron, B. (2009). Development and Validation of a Coupled Eulerian Lagrangian Finite Element Ice Scour Model. Proceedings of the ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering. Volume 5: Polar and Arctic Sciences and Technology; CFD and VIV. The American Society of Mechanical Engineers (ASME): Honolulu USA, OMAE. p 2009-79553 p 87-95. https://doi.org/10.1115/OMAE2009-79553


Barker, A., & Timco, G. (2003). The Friction Coefficient of a Large Ice Block on a Sand/Gravel Beach. In 12th Workshop on the Hydraulics of Ice Cover Rivers, CGU HS Comm. on River Ice Processes and the Environment: Edmonton Alberta Canada.
Babaei, MH., & Sudom, D. (2014). Ice-Seabed Gouging Database: Review & Analysis of Available Numerical Models. Proceedings of Offshore Technology Conference (OTC) Houston TX: OTC-24603-MS. https://doi.org/10.4043/24603-MS

Banneyake, R., Hossain, K., Eltaher, A., Nguyen, T., & Jukes, P. (2011). Ice-Soil-Pipeline Interactions Using Coupled Eulerian-Lagrangian (CEL) Ice Gouge Simulations – Extracts from Ice Pipe JIP. Proceedings of Offshore Technology Conference (OTC) Houston TX: OTC-22047-MS. https://doi.org/10.4043/22047-MS

Choi, KS., & Lee, JH. (2002). A Comparative Study of Ice Scour-Seabed Interaction Models. Journal of Ocean Engineering and Technology, 16(1), 27-35.
Grigoriev, IS., & Meilikhov, EZ. (1997). Handbook of Physical Quantities. CRC Press.
Konuk, I., Yu, S., & Garcia, R. (2005). An ALE FEM Model of Ice Scour. Proceedings of the 11th Inertnational Conference of the International Association of Computer Models and Advance in Geomechnaics Turin Italy.
NAVFAC. (1982). Foundations and Earth Structures, Department of the Navy, Naval Facilities Engineering Command, Washington D.C. USA.
Arnau, S., & Ivanović, A. (2019). Rate Effects During Ice Scour in Sand. Cold Regions Science and Technology, 158, 182-194. https://doi.org/10.1016/j.coldregions.2018.08.019

Truskov, PA., & Surkov, GA. (1991). Scour Depth Distribution on the Northern Sakhalin Offshor. Proceedings of the 1st International Socirty of Offshore and Polar Engineers Conference Edinburgh UK: ISOPE-I-91128.
Woodworth-Lynas, C., Nixon, D., Phillips, R., & Palmer, A. (1996). Subgouge Deformations and the Security of Arctic Marine Pipeline. Proceedings of Offshore Technology Conference (OTC) Houston TX: OTC-8222-MS. https://doi.org/10.4043/8222-MS

- TOOLS
-
METRICS

-
- 6 Crossref
- Scopus
- 4,069 View
- 75 Download
- Related articles in JOET
-
A Comparative Study of Ice Scour-Seabed Interaction Models2002 February;16(1)
Experimental Study on Wedge Slamming Considering Fluid-Structure Interaction2017 ;31(1)