터렛 계류된 FPSO의 운동응답 및 계류선 손상 시 거동 특성에 대한 실험적 연구
Experimental Study of Effect of Mooring Line Failure on Behavior of Turret-moored FPSO Ship
Article information
Abstract
FPSO model tests of mooring line failure were carried out in the ocean basin at KRISO. The characteristics of the motions and mooring lines were investigated. The FPSO ship was moored using an internal turret and catenary mooring. The test model was 1/60 scale. The mooring lines were designed to satisfy the characteristics of the original mooring lines using the truncation method. The experiments were conducted under various environments: a safe wave, current and wind condition; single broken mooring line condition; and transient mode condition. The moment of the break was determined based on experimental test results. The results showed that the FPSO behavior and mooring line tensions were acceptable under the failure condition.
1. 서 론
FPSO(Floating production storage and off-loading)를 설계하기 위해서는 FPSO의 운동과 계류시스템 성능 해석이 필수적이다. 북해에 투입되는 FPSO의 경우, 북해의 환경 특성에 의해 주 터렛 계류시스템이 사용된다. 터렛시스템은 터렛을 중심으로 FPSO의 회전을 허용하여 해상 환경의 방향이 바뀌어도 FPSO의 작업성과 안정성을 높여준다(Cho et al., 2013). 터렛에는 다수의 계류선이 연결되어있는데, FPSO의 과도한 운동과 반복적인 하중에 의해 계류선의 손상이 발생할 수 있다. 최근 산업계에 따르면 최근 14년 동안 43건 이상의 계류선 손상이 발생되었고, 해양구조물 중 FPSO에서 가장 많은 계류선 손상이 나타난 것을 확인할 수 있다(Majhi and Granherne, 2013). 계류선이 손상되면 과도적인 운동이 발생하고(Han et al., 2011), 수평면 운동에 큰 영향을 미치며 다른 운동에는 상대적으로 작은 영향을 미친다(Kim et al., 2014).
계류선이 손상된 후 부유체는 새로운 평형점을 찾아간다(Kurian et al., 2012). 본 논문에서는 계류선 손상 모형실험을 수행하여 계류선 손상시 FPSO의 운동성능과 계류 특성을 실험적으로 평가하였다.
2. 모형실험
2.1 FPSO & Mooring Line Configuration
모형실험은 KRISO 해양공학수조에서 수행되었다. 모형의 축척비는 1/60으로 해양공학 수조의 파랑생성범위와 수조의 크기를 고려하여 결정하였다. 모형실험에 사용한 구조물은 수심 400m에 설치되는 100만 배럴급 FPSO이다. FPSO 모형에는 부가물로 빌지킬이 있다. 터렛은 A.P로부터 선수방향으로 200.6m(LPP기준 75%되는 지점)에 위치한다. Fig. 1과 Table 1에 제작된 FPSO 모형과 주요제원에 대하여 나타내었다. FPSO의 계류시스템은 내부 터렛과 현수선으로 구성되었다. 본 모형실험에서는 터렛은 Weathervane 특성만을 고려하여 회전하는 터렛 실린더와 케이스만을 제작하였다. 제작된 터렛 모형을 Fig. 2에 나타내었다.
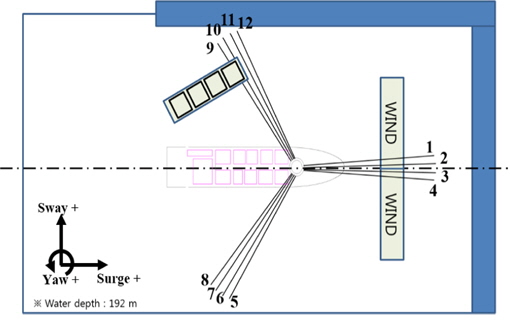
현수선 계류시스템은 체인-와이어-체인 형태의 복합 계류선으로 구성되어있으며 계류선의 제원을 Table 2에 나타내었다. 계류선은 12개의 계류선이 선수, 선미 좌현, 선미 우현으로 향하는 3개의 그룹, 각각의 그룹이 120deg 간격으로 배치되었으며 한 그룹은 4개의 계류선으로 이루어져있다. 해양공학수조의 조파기, 바람발생장치 등을 고려한 모형실험 배치를 Fig. 3에 나타내었다.
2.2 절단계류기법
FPSO가 설치될 해역의 수심은 400m이다. 해양공학수조의 수심은 3.2m로 모형축척비 60인 경우 해양공학수조의 수심은 192m가 되어 원 수심과 약 2배 정도 차이가 난다. 모형실험은 상사법칙에 준하여 실시되는데 이러한 경우 수심에 대한 상사를 만족시킬 수 없어 원래의 계류시스템을 사용할 수 없으므로, 원 수심에서의 운동과 수심의 차이가 나는 공학수조에서 FPSO가 동일한 운동을 하도록 하는 절단계류시스템을 사용해야한다. FPSO의 운동을 동일하게 하기위해서는 절단계류시스템이 원계류시스템의 정적 그리고 동적 특성을 그대로 유지해야한다. 절단계류시스템은 기본적으로 다음의 조건을 고려하여 만들 수 있다.
□ Compatibility for Static Load
- Restoring Characteristics
- Submerged Weight of Mooring Line
- Axial Stiffness of Mooring Line
□ Compatibility for Dynamics Load
- Mass and Diameter of Mooring Line
절단과정의 첫 단계는 절단계수(γ)를 찾는 것이다. 절단계수는 원수심과 절단된 수심의 비이다(Cho et al.,2014). 절단계수를 계류선의 길이, 무게, 축강성에 적용하여 절단 계류선의 물성치와 제원을 구한다. 최종적으로 찾은 계류선 모형은 Fig. 4와 같이 체인-스프링-체인-스프링 조합이다. 체인과 스프링의 길이, 무게, 강성은 Table 3과 같다.
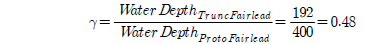
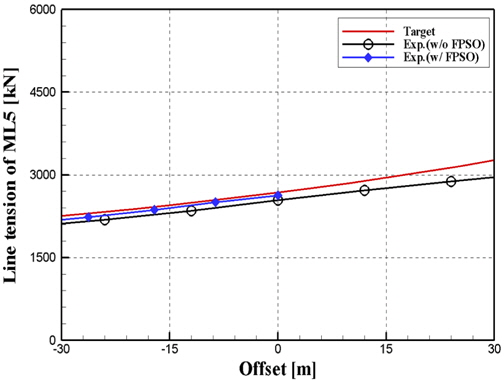
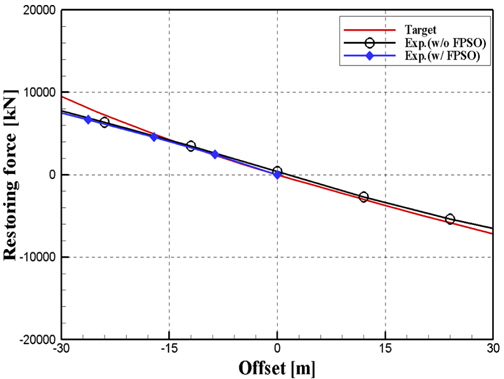
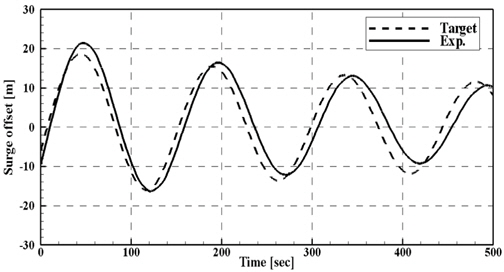
설계된 절단계류시스템의 특성을 파악하기 위하여 1 Line static test를 수행하고 해양공학수조에서 전체 절단계류시스템의 Static pull-out test를 수행하였다. 원수심 상태에서 수치해석 결과의 Offset의 변화가 30m정도인 것을 감안하여 복원력 곡선 특성을 맞추었다. 주어진 Offset에 따라 Fairlead point에서의 장력변화를 표기한 1 Line static test의 결과를 Fig. 5에 나타내었으며, 전체 계류시스템의 복원력 곡선(Restoring force curve)을 Fig. 6에 나타내었다. 계류선의 Fairlead point 부분에 작용하는 Pre-tension은 약 2,400kN이다. 각각의 계류선의 장력 변화는 정성적, 정량적으로 잘 일치하는 것을 확인 할 수 있다. 하지만 복원력 곡선의 경우 절단계수(γ)가 작으면 기하학적 상사에 의해 만족해지는 Offset 변화에 따른 Fairlead의 상대각도가 실제와 다른 상황이 발생한다. 이러한 영향으로 장력 곡선에 비해 복원력 곡선이 Offset의 크기가 커질수록 원 수심의 복원력 차이가 발생하는 것을 확인할 수 있다. 계류시스템의 정적인 상사를 조정한 후 자유감쇠 실험을 수행하였다. 전후동요 방향의 자유감쇠 실험 시계열 데이터를 Fig. 7에 나타내었다. 설계사에서 제공 가진다. 원 수심의 전후동요 고유주기는 145.33sec이며, 절단계류시스템을 적용하여 얻은 고유주기는 148.72sec로 약 2%에 오차를 자유감쇠실험의 결과로 동적인 상사 역시 정성적으로 잘 일치함을 확인할 수 있다.
2.3 손상계류시스템
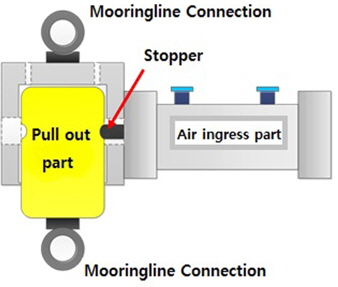
일반적인 계류선 손상은 부유체의 운동이 과도할 때 발생할 가능성이 높다. 계류선 손상 모형실험에서 정확한 운동특성과 계류성능을 평가하기 위해서는 계류선이 손상되는 시점에서 환경하중을 제외한 외력이 없는 상태에서 모형실험이 수행되야한다. 본 모형실험에서는 이러한 점을 고려하여 공기압 트리거(Trigger)를 이용한 장치를 고안하여 모형실험을 수행하였다. Fig. 8에는 공기압 트리거 장치의 계략도를, Fig. 9에는 공기압 트리거 장치의 실제 설치 모습을 나타내었다. 트리거 장치의 중량은 공기 중 23g으로, 수중에서 절단계류시스템의 계류선과 동일한 중량을 가질 수 있도록 15g의 중성부력을 적용하였다. 손상계류 장치 설치 후 Static pull out 실험을 수행하여 복원력 곡선에 변화가 없음을 확인하였다.
손상계류장치는 환경외력에 대한 응답이 가장 큰 1번 계류선에 설치하였다. 또한 계류선이 손상되지 않았을 경우 불규칙파 및 복합환경 조건 실험을 통하여, 전후동요와 계류선의 장력이 최대가 되는 지점을 계측하여 계류선 손상 시점을 정하였다. 계류선의 손상은 대부분 Fairlead 위치 및 커넥터(Connector)에서 발생한다(Morandini and Legerstee, 2009). 모형실험에서 계류선 손상위치는 Fairlead 위치에서 9m 떨어진 지점으로 Fairlead에 최대한 근접한 위치에 손상계류 장치를 설치하였다.
2.4 환경조건
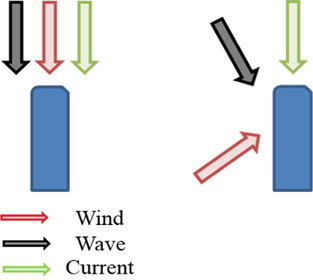
모형시험에 사용된 환경 조건은 불규칙파 조건과 파도, 바람, 조류가 함께 있는 복합환경 조건으로 구성하였다. 복합환경은 환경외력의 방향이 각기 다른 방향(파도 : 210deg, 바람 : 300deg, 조류 : 180deg)에서 입사되는 Non-collinear 조건과 환경외력의 방향이 180deg로 동일한 Collinear 조건으로 구성하였다. 환경외력의 입사방향을 Fig. 10, 환경조건을 Table 4에 나타내었다.
불규칙파는 JONSWAP 스펙트럼(γ=3.3)을 사용하였다. 불규칙파는 실선 기준 3시간 10분으로 생성하였으며 파도의 발달을 고려하여 파도 생성 후 실선 기준 10분 후 데이터 계측을 수행하였다. 모형시험은 모든 계류선이 온전한 Intact조건, 하나의 계류선을 손상시킨 상태의 1 Line broken 조건 그리고 최대 밀림 발생지점에서 계류선을 손상시킨 Transient 조건으로 구성하였다.
3. 모형실험 결과
3.1 Results of intact test
FPSO의 거동 및 계류선 장력 변화를 평가하기 위해 복합환경 실험을 수행하였다. 선수동요에 대한 통계해석 결과와 각각의 계류선 장력의 평균 값을 Collinear 조건과 Non-collinear 조건으로 비교하여 Fig. 11, 12에 나타내었다. 터렛의 특징 중 하나는 주된 환경외력 방향으로 선수각이 회전(Weathervane)하는 것이다.
Weathervane 특성을 파악하기 위한 실험적, 수치적 연구가 이루어지고 있다. 장주기 표류력과 조류(Current)에서 발생할 수 있는 Weathervane 안정성에 대한 연구가 수행되었으며(Bernitsas and Papoulias, 1986) 파주기에 따라 발생하는 과대 선수동요를 부유체에 작용하는 표류력과 모멘트의 평형으로 설명하였다(Liu et al., 1999). 터렛의 위치 변화에 따른 규칙파에서 FPSO 거동 특성을 실험을 통해 고찰하였으며(Kannah and Natarajan, 2006), 터렛 위치와 파도 주기에 따른 과대 선수동요에 대한 수치해석을 수행하여 과대 선수동요 발생 주기를 확인하였다(Yadav et al., 2007).
Collinear 조건 실험 결과 평균 선수동요 값은 15.45deg이며 평균 전후동요(Surge) 값은 - 17.12m이다. 환경외력의 방향이 선수방향으로 동일하기 때문에 선수그룹인 계류선 1~4번의 평균 장력이 다른 선미 좌, 우 그룹의 평균 값보다 큰 것을 확인할 수 있다. Non-collinear 조건 실험 결과 환경외력이 각기 다른 방향에서 입사되기 때문에 평균 선수동요 값이 68.37deg로 증가하는 것을 확인할 수 있다. 평균장력의 경우 조류와 바람의 입사각에 의한 영향으로 Collinear 조건과는 다르게 9~12번 계류선의 평균 장력이 선수그룹에 위치한 1~4번 계류선의 평균 장력 값보다 증가했음을 확인할 수 있다. Non-collinear 조건에서 평균 선수동요 값이 68.37deg로 나타난 것은 바람(입사각 300deg, 풍속 44.39m/s)의 일정한 하중의 영향이 큰 것으로 판단된다. Collinear 조건에서 계류선에 작용하는 최대 장력은 5,198kN이며 Non-collinear 조건에서의 최대장력은 4,868kN으로 안전율(Safety factor, Intact=1.67)을 고려할 시 8,680kN으로 최대 항복응력인 12,496kN 보다 작은 것을 확인할 수 있다.
모형시험 결과를 살펴보면 Collinear 조건에서 선수동요가 zero mean을 가지지 않는 것을 확인할 수 있다. 이는 Wind의 Projection area의 좌우 대칭이 성립하지 않는 구조에 의한 영향과 상대적으로 짧은 터렛 위치로 인한 모멘트 팔의 길이의 감소로 기인한 선수동요 안정성의 감소로 나타나는 현상임을 나타낸다.
3.2 Results of 1 line broken test
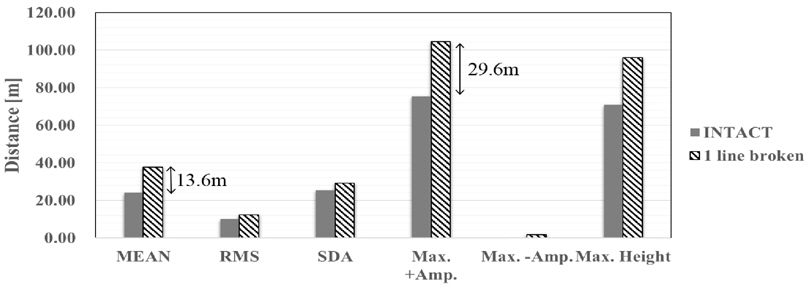
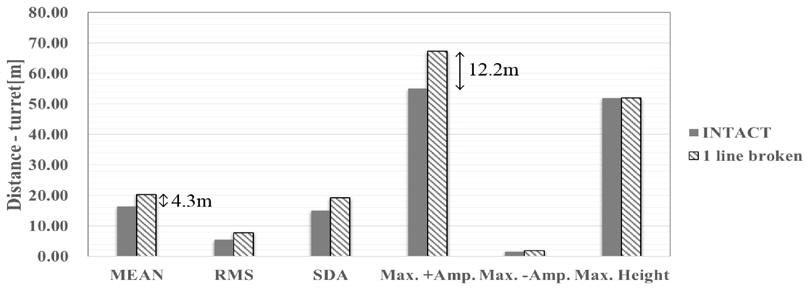
계류선 손상 후 계류시스템의 거동특성을 정량적으로 분석하기 위하여 Intact 조건과 1 Line broken 조건에서 복합환경 모형실험을 수행하였다. 손상계류선은 수치해석 및 Intact 조건의 모형실험 결과에서 가장 큰 장력변화를 보인 1번 계류선으로 정하였다. 정량적인 분석을 위하여 Fig. 13~14에 전후동요와 좌우동요의 응답을 이용하여 터렛의 이동거리를 계산하여 비교하였다. 계류선이 손상되었을 때 Collinear조건의 경우 평균 밀림이 13.6m, 최대 밀림이 29.6m 증가하는 것을 확인할 수 있다. Non-collinear 조건의 경우에는 평균 밀림이 4.3m, 최대 밀림이 12.2m로 collinear 조건보다 작은 변화를 가져오는 것을 확인할 수 있다. 이는 환경외력이 Non-collinear 조건에서는 분산되어 입사되는 영향으로 보인다.
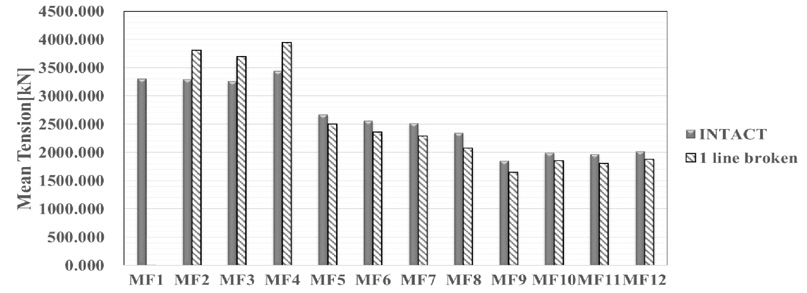
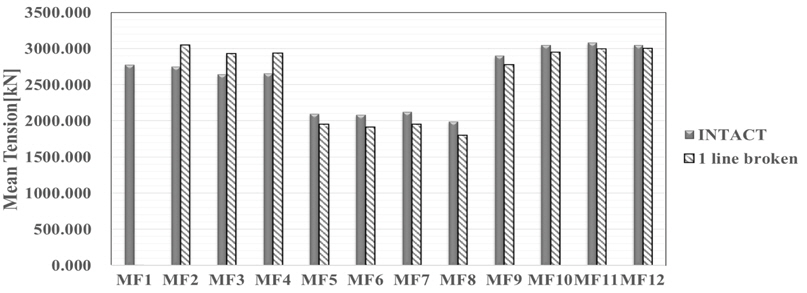
Intact 조건과 1 Line broken 조건에서 평균 장력을 Fig. 15~16에 나타내었다. 앞선 밀림의 결과와 마찬가지로 Collinear 조건의 변화가 Non-collinear 조건의 변화보다 큰 것을 확인할 수 있다. Collinear의 경우 선수방향 계류선 평균 장력이 500kN 정도 증가함을 확인할 수 있으며 Non-collinear 조건의 경우 300kN 정도의 증가함을 확인 할 수 있다. 1 Line broken 조건에서 계류선에 작용하는 최대장력은 6,667kN(Collinear), 5,205kN(Non-collinear)로 Collinear 조건의 경우 약 1500kN, Non-collinear 조건의 경우 약 300kN의 증가를 보인다. 계류선이 손상된 상태에서 파주파수 성분에 의한 FPSO의 거동과 저주파수 운동의 변화를 비교해보기 위하여 모형실험의 시계열을 FFT분석하였다. Bandpass filter를 사용하여 파주파수 성분(0.03~2hz)만을 비교하여 Table 5에 나타내었고, 저주파수 영역(0~0.03hz)만을 비교하여 Table 6에 나타내었다. 파주파수 성분만을 고려한 해석 결과 Collinear 조건에서는 Intact과, 1 Line broken의 평균 전후동요 밀림은 약 7% 정도의 차이를 보이며, 저주파수 성분만을 고려하였을 때는 약 44%의 차이를 보인다. 이는 계류선의 손상이 저주파수 운동에 영향을 주는 것으로 판단된다.
3.3 Transient test result
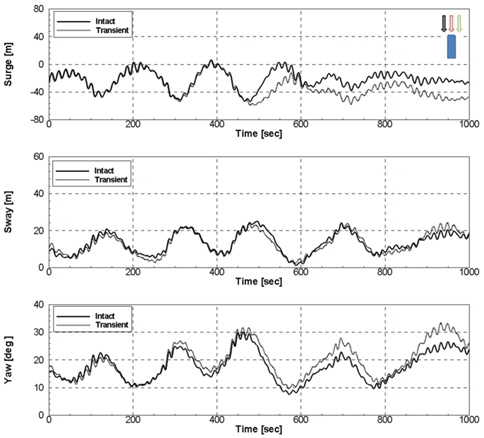
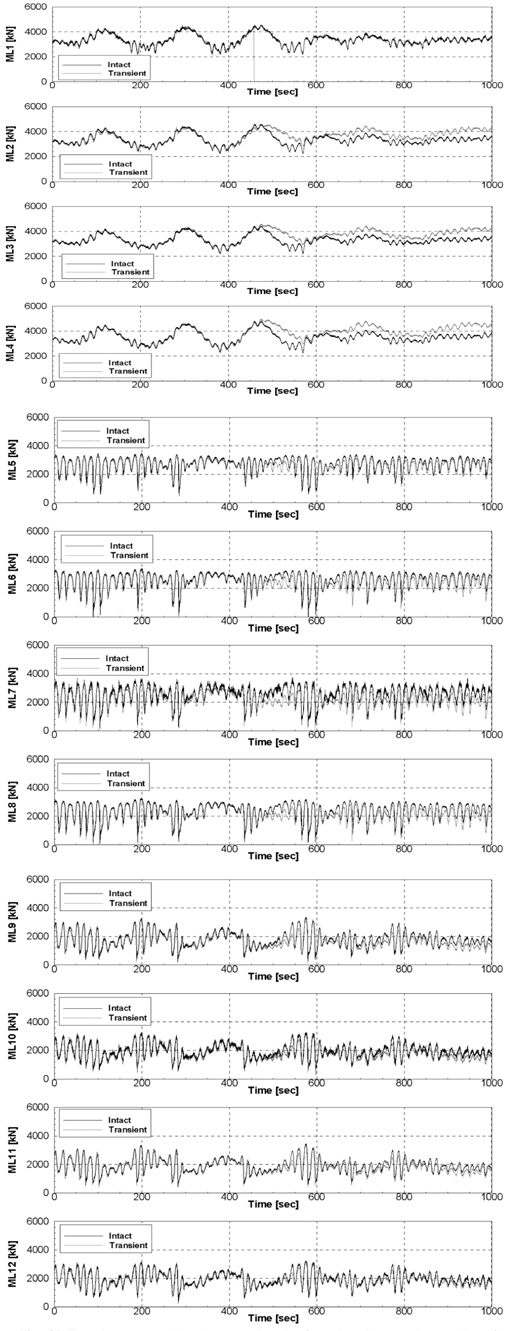
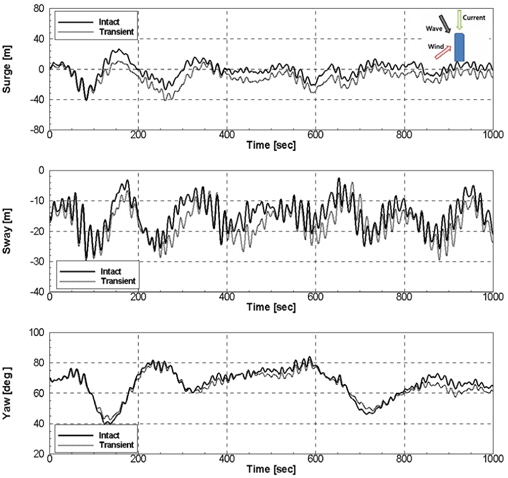
환경응답 중 계류선 손상 시 운동응답 및 거동 특성을 살펴 보기위해 Transient 조건의 모형실험을 수행하였다. 비 손상 계류된 FPSO의 모형실험(Intact)을 통하여 FPSO의 전후동요가 가장 큰 시점을 계측하고, 손상계류장치를 사용하여 동일한 시점에서 계류선을 절단하였다. 계류선 손상 시점을 Fig. 17에 나타내었다. 일반적으로 불규칙파는 실선 기준 3시간을 생성하여 모형실험을 수행한다. 하지만 계류선이 손상되는 시점과 과도한 운동응답이 나타나는 시점은 순간적이므로 전체 시계열을 나타내지 않고 계류선이 손상되는 시점을 확대하여 표시하였다(Fig. 18~21). Fig. 18과 19에 Collinear 조건에서 Transient 조건과 Intact 조건의 시계열 비교 그래프를 나타내었다. Collinear 조건에서 Transient 실험 결과 계류선 손상 후 선미 쪽으로의 밀림과 선수 쪽 계류선의 장력 증가를 관찰할 수 있다. 하지만 다른 두 그룹의 계류선 장력변화는 적은 것으로 보인다. Fig. 20와 21에 Non-collinear 조건에서 Transient 조건과 Intact 조건의 시계열 비교 그래프를 나타내었다. Non-collinear 조건에서 Transient 실험 결과 Collinear 조건 보다 작은 밀림과 장력 변화를 관찰할 수 있다. 이는 앞서 말한 이유와 같이 환경외력의 입사각이 서로 다르기 때문으로 볼 수 있다.
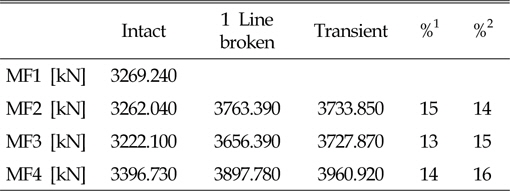
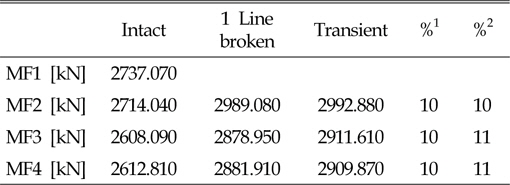
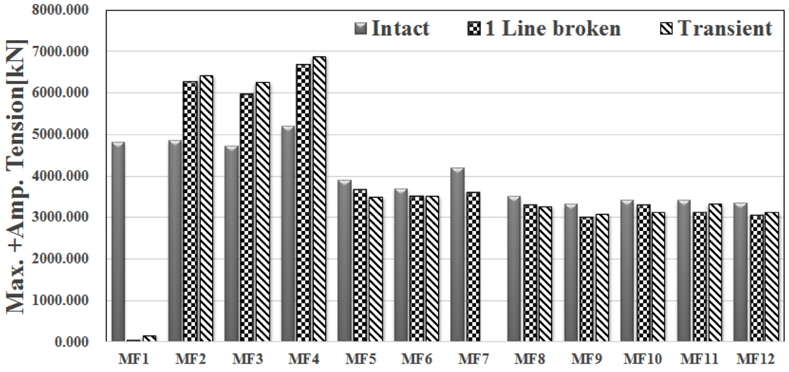
Intact, 1 Line broken, Transient 조건에서 평균장력의 변화를 Table 7과 8에 나타내었다. Collinear 조건의 경우 3가지 조건의 것을 확인할 수 있다. 이는 환경외력의 입사각들이 같은 경우 장력변화는 15% 정도, Non-collinear 조건의 경우 10% 정도인 계류선 손상 시 큰 계류선장력 변화를 야기할 수 있다. 계류선 손상 시 장력 변화가 큰 Collinear 조건에서 Intact, 1 Line broken 그리고 Transient 상태에 계류선에 작용하는 최대장력을 Fig. 22에 나타내었다. 계류선에 작용하는 최대 장력은 6,870kN 으로 손상상태의 안전율(Safety factor, damaged=1.25)을 고려할 때 작용하는 장력은 8,587kN으로 계류선의 MBL인 12,496kN 이하로 안전함을 알 수 있다.
4. 결 론
본 논문에서는 터렛 계류된 100만 배럴급 FPSO의 운동 및 계류선 손상 모형실험을 수행하였다.
(1) 절단계류기법을 사용하여 등가의 계류시스템을 설계하고, 트리거 장치를 사용한 계류선 손상을 모형실험적인 방법으로 접근하였다.
(2) 복합환경에서 모형실험을 수행하여 FPSO의 운동 및 계류시스템 특성과 손상 계류시 거동 및 계류시스템의 특성을 계측하였다.
(3) 계류선 손상 시 수평면 운동의 변화와 선수방향 계류선의 장력변화를 확인하였다.
(4) 환경외력에 의한 FPSO의 동적 거동 중 계류선을 손상실험을 수행하여 순간적으로 과도한 운동응답이 발생하는 것을 확인할 수 있었다.
추가적인 연구로 거동 중인 FPSO의 계류선 손상 시점을 달리하여 거동특성을 파악하고 수치해석과의 검증과정이 필요며 피로해석을 통한 계류수명 평가역시 수행되어야 할 것으로 판단된다.
Notes
It is noted that this paper is revised edition based on proceedings of KAOST 2014 in Jeju.
Acknowledgements
본 연구는 산업통상자원부의 산업융합원천기술개발사업 “설계 유의파고 15m 해역의 Oil & Gas 생산을 위한 100만 배럴급 FPSO용 Turret system 설계 기술 개발(3차년도)”과 해양수산부의 해양장비개발 및 인프라구축사업 “심해공학수조 운용을 위한 연구인프라 구축 및 심해플랜트 Pre-FEED 원천핵심기술개발”의 결과 중 일부임을 밝힌다.
References
Bernitsas, M.M., Papoulias, F.A., 1986. Stability of Single Point Mooring Systems. Applied Ocean Research, 8(1), 49-58.
Bernitsas M.M., Papoulias F.A.. Stability of Single Point Mooring Systems. Applied Ocean Research 1986;8(1):49–58. 10.1016/S0141-1187(86)80031-1.Cho, S.K., Sung, H.G., Hong S.Y., Kim Y.H., Choi, H.S., 2013. Study of the Stability of Turret moored Floating Body. Proceedings of International Ship Stability Workshop, Brest, ISSW, 892-898.
Cho S.K., Sung H.G., Hong S.Y., Kim Y.H., Choi H.S.. Study of the Stability of Turret moored Floating Body In : Proceedings of International Ship Stability Workshop. ISSW; Brest: 2013. p. 892–898.Cho, S.K., Hong, J.P., Sung, H.G., Kim, Y.H., Kim, B.W., Kim, D.W., Seo, J.H., 2014. Model Test of Turret Moored FPSO: Truncation of Mooring. Proceeding of KAOSTS, Busan KOREA, 1978-1981.
Cho S.K., Hong J.P., Sung H.G., Kim Y.H., Kim B.W., Kim D.W., Seo J.H.. Model Test of Turret Moored FPSO: Truncation of Mooring In : Proceeding of KAOSTS. Busan KOREA: 2014. p. 1978–1981.Han, J.S., Son, Y.J., Rho, J.B., Choi, H.S., 2011. The Transient Behavior of Mooring Systems in Line-Broken Condition. Proceedings of International Offshore and Polar Engineering Conference.
Han J.S., Son Y.J., Rho J.B., Choi H.S.. The Transient Behavior of Mooring Systems in Line-Broken Condition In : Proceedings of International Offshore and Polar Engineering Conference; 2011.annah, T.R., Natarajan, R., 2006. Effect of Turret Location on the Dynamic Behaviour of an Internal Turret Moored FPSO System. Journal of Naval Architecture and Marine Engineering, 3, 23-37.
Kannah T.R., Natarajan R.. Effect of Turret Location on the Dynamic Behaviour of an Internal Turret Moored FPSO System. Journal of Naval Architecture and Marine Engineering 2006;3:23–37.Kim, B.W., Sung, H.G., Hong, S.A., Hong, S.W., 2014. Dynamic Coupled Analysis of FSRU with Broken Mooring Line. Proceedings of International Offshore and Polar Engineering Conference.
Kim B.W., Sung H.G., Hong S.A., Hong S.W.. Dynamic Coupled Analysis of FSRU with Broken Mooring Line In : Proceedings of International Offshore and Polar Engineering Conference; 2014.Kurian, V.J., Yassir, M.A., Harahap, I.S.H., 2012. Dynamic Response of Semisubmersibles with Damaged Mooring Lines. Proceedings of International Offshore and Polar Engineering Conference.
Kurian V.J., Yassir M.A., Harahap I.S.H.. Dynamic Response of Semisubmersibles with Damaged Mooring Lines In : Proceedings of International Offshore and Polar Engineering Conference; 2012.Liu, F., Brown, D.T., Fang, J., 1999. Yawing of Turret-Moored Monohull Vessels in Response to Regular Waves. Journal of Ship Research, 43(3), 135-142.
Liu F., Brown D.T., Fang J.. Yawing of Turret-Moored Monohull Vessels in Response to Regular Waves. Journal of Ship Research 1999;43(3):135–142.Majhi, S., Granherne, R.D., 2013. Application of Lessons Learned From Field Experience to Design, Installation and Maintenance of FPS Moorings - Proceeding of Offshore Technology Conference, Texas, USA, OTC 24181
. Majhi S., Granherne R.D.. Application of Lessons Learned From Field Experience to Design, Installation and Maintenance of FPS Moorings - In : Proceeding of Offshore Technology Conference. Texas, USA; 2013. OTC 24181.Morandini, C., Legerstee, F., 2009. Consistent Integrity of Mooring System, Proceedings of International Offshore and Polar Engineering Conference.
Morandini C., Legerstee F.. Consistent Integrity of Mooring System In : Proceedings of International Offshore and Polar Engineering Conference; 2009.Yadav, A., Varghese, S., Thiagarajan, K.P., 2007. Parametric study of yaw instability of a weathervaning platform. 16th Australasian Fluid Mechanics Conference, 2007, 1012-1015.
Yadav A., Varghese S., Thiagarajan K.P.. Parametric study of yaw instability of a weathervaning platform In : 16th Australasian Fluid Mechanics Conference; 2007. 2007p. 1012–1015.