실시간 적응 A* 알고리즘과 기하학 프로그래밍을 이용한 선박 최적항로의 2단계 생성기법 연구
Two-Phase Approach to Optimal Weather Routing Using Real-Time Adaptive A* Algorithm and Geometric Programming
Article information
Abstract
This paper proposes a new approach for solving the weather routing problem by dividing it into two phases with the goal of fuel saving. The problem is to decide two optimal variables: the heading angle and speed of the ship under several constraints. In the first phase, the optimal route is obtained using the Real-Time Adaptive A* algorithm with a fixed ship speed. In other words, only the heading angle is decided. The second phase is the speed scheduling phase. In this phase, the original problem, which is a nonlinear optimization problem, is converted into a geometric programming problem. By solving this geometric programming problem, which is a convex optimization problem, we can obtain an optimal speed scheduling solution very efficiently. A simple case of numerical simulation is conducted in order to validate the proposed method, and the results show that the proposed method can save fuel compared to a constant engine output voyage and constant speed voyage.
1. 서 론
최근 환경에 대한 문제와 선박의 연료비 문제로 선박의 온실가스 배출 및 연료비 절감을 위한 연구가 활발이 이루어 지고있다. 이를 위하여 선박의 정해진 설계 속도의 60% 정도의 속도로 저속운항을 하거나 선체에 부가물을 붙여 저항을 감소시키는 등의 노력들이 이루어지고 있다(He-ping, 2007). 최적항로 계획은 이러한 연료 소비량 감소 및 온실가스 배출 감소를 위한 노력의 하나로 주어진 해상환경에서 최소의 연료로 목적지까지 도달하기 위한 경로 생성에 관한 연구이다. 이와 관련하여 알고리즘 방법론에 관한 연구로는 3차원 동적 프로그래밍을 이용하여 선박의 속도와 경로를 변경 시켜가며 경로를 도출 한 연구와(Shao et al., 2012), 수정된 등시선법을 이용하여 기존의 그리드 기반의 경로 탐색에서 벗어난 방법(Rho, 2013) 등이 있다. 하지만 주어진 환경에서 전역 최적화의 보장이 없으며, 등시선법을 통한 알고리즘에 의한 완전성이 보장되지 않았으므로 생성된 결과에서 최적화의 정도가 낮을 수 있다는 단점이 있다. 최적항로 도출 문제의 특징으로 언급 되는 해상 환경 변화의 문제를 해결하기 위하여 Hinnethal and Clauss (2010)은 앙상블 일기 예보를 도입하여 환경 변화에 강건한 최적항로를 도출하였다. 하지만 이 앙상블 일기예보는 상당히 비싼 정보이며, 방대한 데이터베이스를 바탕으로 한 계산이 이루어져야 하므로 항로 도출에 계산 시간이 많이 걸린다는 단점이 있다. 그러므로 환경 변화를 반영하는 동시에 연료 소모량 측면에서 최적화된 항로를 도출하기 위해서는 해상 환경 예보가 바뀌는 시간 단위에 따라 적절한 시간 내에 계산이 가능한 방법이 필요하다. 본 논문에서는 효율적인 계산 시간과 높은 정도의 경로 최적화를 위하여 항로 도출에 실시간 적응 A* 알고리즘과 기하학적 프로그래밍을 바탕으로 최적항로 도출 방안을 제시하고자 한다. 선박의 경우 연산시간의 여유가 큰 편이나, 수백 척의 선박을 운영하는 대형 해운사의 경우 각각의 선박이 기상상태를 전송 받고 최적경로를 생성하는 것 보다는 중앙관제센터에서 업데이트 된 기상상태를 바탕으로 수십척 이상의 운항중인 선박의 최적경로를 생성하고 각 선박에게 전송하는 통합 운영방식이 최적경로 시스템 및 기상상태 서비스의 개수를 최소화시킬수 있다는 점에서 경제적인데, 이런 경우 계산시간의 중요성이 증가하고 본 논문에서 제시한 기법으로 최적경로 생성에 소요되는 계산시간을 감소시킬 수 있다.
본 논문은 다음의 순서로 구성되어 있다. 우선 최적항로의 문제의 특성을 이야기 하고 다음 장에서는 해상 환경에 의한 선박 속력 저하를 고려하기 위한 계산 방법과 항해에서 반드시 고려되어야 하는 안전성의 반영 방안을 제시한다. 네 번째 장에서는 항로 도출을 위해 적용된 실시간 적응 A* 알고리즘에 대한 간단한 설명과 기본적인 이해를 위해 A* 알고리즘에 대한 설명을 덧붙인다. 그리고 제 5장에서는 이렇게 도출된 항로에서 최적의 선박 운항 전략을 제시하기 위한 방법인 기하학적 프로그래밍에 대한 설명과 이를 어떻게 최적항로 문제에 적용시킬 것인가에 대한 논의를 한다. 다음 장에서는 간단한 수치 시뮬레이션을 통한 이 방법의 효용성을 검증하고 마지막 장에서는 본 논문의 결론과 요약을 제시하고자 한다.
2. 문제의 정의
최적항로 문제에서는 해상환경이 시시각각 다양하게 변화하며 기상 정보를 제공하는 기관에서 주어지는 정보가 한정적이기 때문에 완벽한 최적화를 이룰 수 있는 항로를 도출 하는 것이 어렵다. 그러므로 해상 환경이 업데이트 되는 각 시간 간격마다 새롭게 최적항로를 도출하는 것이 요구된다. 또한 각 시간 간격 마다 최적항로를 만들어내야 하기 때문에 이를 위한 적절한 알고리즘의 적용이 요구된다. 이 때 주어지는 최적화 문제는 각 시간 간격 별 선박의 방향각과 속도 두 변수를 결정하는 것이고, 문제의 식은 다음과 같이 정의 될 수 있다.
여기서 Vi−1,i값은 i−1번째 스텝의 위치에서 i번째 스텝까지의 속력, g (Vi−1,i)는 단위 거리당 연료 소모 값을 뜻하며 선박의 시운전 데이터를 통해 얻을 수 있다. 일반적으로 이 값은 속력에 대한 이차함수 형태로 표현이 가능하다. gad (Vi−1,i, βi−1,i) 값은 속도 Vi−1,i를 유지하기 위한 해상환경에서의 연료 보상 량을 뜻한다. 첫 번째 제약 조건은 총 항해 시간이 정해진 시간 T내에 항구에 도착해야 함을 의미하며, 두 번째 제약 조건은 선박의 운항 속도 영역과 세 번째 조건은 선박의 방향각의 제약 조건을 나타낸다. 이 문제를 해결하기 위한 기본적인 아이디어는 다음 Fig. 1로 설명할 수 있다. 매 여섯 시간 마다 업데이트 되는 일기 예보를 바탕으로 Phase 1에서 선박 속도를 고정하고 Real Time A* 알고리즘을 이용하여 최적항로를 생성하고 Phase 2에서는 Phase 1을 통해 생성된 최적항로에서 기하학 프로그래밍을 이용하여 최적 운항 속도를 계획한다.
Flow Chart of Proposed Idea
3. 최적 항로 생성을 위한 고려 사항
본 논문에서는 최적 항로 생성을 위한 고려 사항으로 해상환경에 의한 선속의 변화량과 선박의 항해중 안전성을 고려하였다. 이들 두 요소는 최적항로 생성을 위한 가장 중요한 요소로써 선속의 변화는 Phase 1과 2에서 안전성은 Phase 2에서 반영된다.
3.1 해상 환경에 의한 선속의 변화
선박이 실제 운항에서 파와 바람을 만나게 되면 선박 속력의 변화가 일어난다. 이 선박의 속력 저하를 정확히 계산하기 위해서는 선박의 부가저항을 계산하여 반영하여야 하지만 이는 푸는 과정에서 시간이 오래 걸리며 방법이 지나치게 복잡하므로 선박의 최적 항로 생성 도출에 과도한 시간이 소요될 수 있다. 그러므로 본 논문에서는 Beaufort number (BN)을 기반으로 한 선박속력 저하식을 이용하도록 한다.(Townsin and Kwon, 1993)이 약산식은 다음과 같이 주어진다.
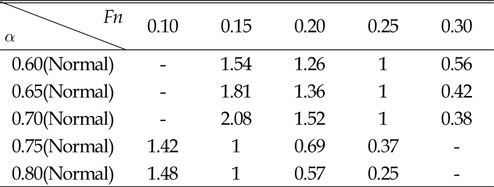
여기서, BN은 Beaufort number, ▽은 선박의 배수량, α는 선속과 선박의 방형계수에 따른 수정 계수, μ는 파와 바람이 들어오는 방향에 따라 달라지게 되는 상수를 뜻한다. △V와 V는 선박의 속력 손실량과 선박의 정수중의 속력을 각각 뜻한다. 위의 식에서 나오는 상수 α와 μ는 다음 표 1과 2와 같다.
α Value
μ Value
3.2 선박의 항해 중 안전성의 반영
본 논문에서 선박의 항해 중 안전성의 반영은 IMO(International Maritime Organization)에서 제시된 항해 안전성에 대한 가이드라인(IMO, 2007)에 따르도록 한다. 여기서 정의되는 각도 β는 선박과 파가 만나게 되는 상대적인 각도로 0도일 때를 Head sea 그리고 180도 일 때를 Following sea로 정의한다.
IMO 가이드라인에서 피해야 하는 상황은 크게 Surf-riding and broaching-to와 과도 횡동요(Parametric-rolling)으로 나뉠 수 있다. 우선 Surf-riding and broaching-to는 파가 뒤에서 오게 될 때 선박의 후미부를 쳐 순간적으로 조종성을 잃게 되어 과도한 Yawing 현상이 발생되고 이때 측면에서 치는 파에 의해 선박의 횡동요가 크게 야기될 수 있는 현상을 말한다. 이 현상은 일반적으로 다음 두 조건이 만족할 때 일어나게 된다.
또 하나의 피해야 하는 현상은 과도횡동요이다. 이는 선박의 고유 주기와 파와 선박의 조우주기가 비슷하게 되어 선박의 과도한 횡동요를 발생시켜 선박의 전복을 야기할 수 있는 현상이다. IMO 가이드라인에 따르면 이 현상은 다음 둘 중의 하나를 만족하게 될 때 일어날 수 있다.
여기서 TR는 선박의 고유 주기이며 TE값은 파와 선박의 조우 주기로 다음과 같이 나타낼 수 있다.
여기서 TW는 파의 주기이며 V선박의 속력으로 노트단위이다. 이 두 가지의 현상 중 하나라도 일어날 가능성이 있으면 Phase 1 에서 그 노드에 값을 무한대로 부여하여 위험가능성이 있는 지역을 피해갈 수 있게 하였다.
4. Phase 1 : 최적 항로 생성
첫 번째 단계에서는 연료 소모량을 기준으로 한 선박의 최적 항로가 주어진다. 이 단계에서는 선박의 속력을 고정시킨 후 선박의 각 구간별 방향각을 결정하게 된다. 해상환경이 일반적으로 그리드 셀의 형태로 주어지게 되므로, 그리드 셀 기반의 길 찾기 방법을 사용하는 것이 타당할 수 있다고 할 수 있다. 본 논문에서 사용한 길찾기 알고리즘은 기존의 A* 알고리즘을 변형하여 계산속도에서 향상을 가져올 수 있는 Real-Time Adaptive A* (RTAA*) 알고리즘을 사용하였다. 이 알고리즘의 기본적인 형태는 A* 알고리즘과 같지만, 휴리스틱 값을 업데이트 하는 부분에서 다르다고 할 수 있다. A* 알고리즘과 RTAA* 알고리즘의 기본적인 구조는 다음과 같다.
4.1 A* 알고리즘
A* 알고리즘(Russell et al., 1995)은 전역 최적화 그리드 셀구조의 맵에 전역 최적화 알고리즘인 다익스트라 알고리즘에 휴리스틱 값을 더하여 속도를 높인 알고리즘으로 이 휴리스틱 값이 Admissible하면 길 찾기의 결과는 다익스트라 알고리즘을 통해 구해진 경로와 같다. 여기서 Admissible하다는 것은 휴리스틱 값이 실제 소요될 값 보다 크게 추정되지 않은 것을 뜻한다. A* 알고리즘의 구조는 두 개의 구조로 이루어져 있다. 앞으로 탐색되어야 할 노드들중 우선순위 노드들이 저장되는 Open Set 그리고 이미 탐색된 노드들로 구성되어 있는 Closed Set로 구성되어 있다. 이때 탐색되어야 할 노드들의 우선순위는 평가 함수(Evaluation function)계산을 통해 그 값이 작은 노드들부터 이루어 진다. 이 평가 함수는 휴리스틱 값과 코스트 값의 합으로 이루어진다. 코스트 값은 현재 위치에서 다음 위치까지 갈때의 정확한 소요 값을 뜻하며, 휴리스틱 값은 다음 노드에서 최종 목적지 까지 갈 때의 추정되는 소요 값을 나타낸다. 다음은 A* 알고리즘을 통해 경로를 생성할 때의 과정을 나타낸다.
Step1. 주어진 그리드 셀 시스템에서 시작점과 도착점을 설정
Step2. Closed set을 공집합으로 설정, Open set에 시작점을 삽입하고 노드에 할당된 값을 0으로 설정, 시작점을 제외한 모든 노드에 대한 값을 무한대로 설정
Step3. Open set에서 가장 작은 값을 가지는 노드에서 노드 연결 관계를 이용하여 평가 함수를 계산
Step4. Step3에서 사용된 노드를 Closed set에 삽입, 새롭게 계산된 노드를 Open set에 삽입
Step5. if) Open set에 삽입된 노드가 최종 목적지면 알고리즘을 종료, otherwise) Step3와 Step4를 반복
Step6. 최종목적지부터 Backstepping하여 최적의 경로 생성
4.2 Real-Time Adaptive A* 알고리즘
Real-Time Adaptive A*(RTAA*) (Koenig and Likhachev, 2006) 알고리즘은 기본적으로 A* 알고리즘의 구조와 같으나 환경이 바뀌었을 경우 휴리스틱 값의 업데이트 과정에서 좀 더 양질의 휴리스틱 값을 제공하여 검색 속도를 높일 수 있다는 장점이 있다. RTAA*에서 휴리스틱 값을 주는 방법의 아이디어는 최초에 경로 탐색을 할 때 나오게 되는 경로 값을 다음 경로 찾기를 할 때 사용한다는 것이다. 이 때 사용되는 휴리스틱 값이 Admissible하다는 것을 다음 식으로 보일 수 있다.
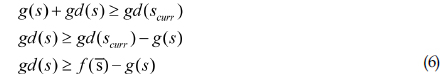
여기서 s는 최초 길찾기를 할 때 탐색이 되었던 노드를 의미하며, g(s)는 현재 위치한 노드 scurr에서 노드 s까지 갈 때의 소모값, 그리고 gd(s)는 노드 s에서 최종 목적지 까지 갈 때의 소모값을 뜻하며, gd(scurr)은 현재 위치한 노드에서 최종 목적지 까지 갈 때의 소모값을 뜻한다. 이 값들은 처음 길 찾기를 할 때 이미 계산 된 값이므로 A* 알고리즘의 Closed set에 저장되어 쉽게 계산이 가능하다. 최초 길 찾기가 끝난 상태일 때, 현재 위치에서 최종 목적지 까지 가는 거리는 자연스럽게 탐색된 노드 s를 거쳐 도착하는 거리의 값보다 작거나 같게 된다. 이는, 다음 탐색될 노드 s에서 좀 더 정확한 정보의 휴리스틱 값을 주는 것과 같고, 실제 소요값보다 적게 되어 Admissible 하다는 것을 뜻한다. 즉, RTAA*에서는 이 휴리스틱 값을 앞선 단계에서 계산된 값을 이용하여, 휴리스틱 값을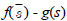 
으로 하여 노드 탐색의 속도를 높여줄 수 있다. RTAA*를 이용하여 최적 경로 생성 과정은 다음과 같다.
Step1. A* 알고리즘의 Step1-4를 수행
Step2. Closed set에 저장된 노드들을 대상으로 휴리스틱 값을
로 업데이트Step3. Step2의 휴리스틱 값을 바탕으로 A* 알고리즘을 수행
Step4. Step2와 3을 반복, 현재 노드가 최종목적지이면 중단
4.3 최적항로 문제에 적용
최적항로 문제에 RTAA* 알고리즘을 적용하기 위해서 본 논문에서는 선박의 속력을 고정시키고 방향각을 정하여 최적항로를 생성하였다. 이때 사용된 평가함수는 다음과 같이 쓰여질 수 있다.
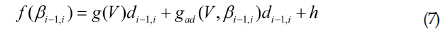
여기서 g(V)는 선박이 속도 V로 정수중에서 운항하게 될 경우 소요되는 단위거리당 연료 소모량을 뜻하며, di−1,i는 i−1번째 스텝에서 i번째 스텝의 노드로 가게 될 때의 거리를 뜻한다. 정수 중 운항 중일 경우 이 함수는 선박의 방향각에 영향을 받지 않게 되고 오로지 선박의 속력의 이차함수 형태로 표현될 수 있다. gad (V, β i−1,i) 값은 선박이 속도 V로 어떤 특정한 해상환경에서 운항하게 될 때 속도 V를 유지하기 위한 단위거리당 추가 연료 소모량을 뜻한다. 평가함수 식 우변의 첫 두항 g(V) di−1,i + gad (V, β i−1,i) di−1,i의 값은 현재 위치에서 다음 위치까지 갈 때의 정확한 연료 소모량을 뜻하므로, 코스트 값의 역할을 한다. 마지막 항인 h값은 휴리스틱 값으로, 최초 A* 알고리즘을 통해 항로를 생성할 때 BN = 2일 때의 값을 적용하여 다음 위치에서 최종 목적지까지의 연료 소모값을 추정하였다. 이 값은 시행착오에 의해 얻어진 값으로, 다익스트라 알고리즘과 비교하여 같은 경로가 나오게 될 때의 값을 이용한 것이다. 해상환경이 바뀌게 되고 선박의 위치가 업데이트 되면, 이 휴리스틱 값은 RTAA*에서 기술되는 휴리스틱 값으로 업데이트가 된다. 이 값은 앞선 단계에서 A* 알고리즘을 통해 계산되어 Closed set에 저장된 값을 이용하여, h = Ji, final − g(V)di−1,i으로 업데이트 한다. 여기서 Ji, final값은 i번째 스텝의 선박의 위치에서 최종 위치까지 이전 단계 A* 알고리즘에서 계산된 총 연료값을 의미한다.
5. Phase 2 : 속도 계획 단계
속도 계획은 Phase 1에서 도출 된 최적 경로를 바탕으로 이루어진다. 이 단계에서는 속도를 계획 하므로, 선박의 방향각이 아닌 선박의 속력이라는 변수를 결정하는 단계이다. 이때 주어지는 최적화 문제의 식은 다음과 같이 주어질 수 있다.
여기서 g(V, i−1,i)는 정수중에서 선박이 속력 V, i−1,i를 유지할 때 소요되는 단위 거리당 연료 소모량이며, △V, i−1,i는 해상 환경에 의해 줄어드는 선박의 속력 손실량을 뜻한다. 여기서 주어지는 연료 소모량 함수는 앞서 언급했듯이 일반적으로 속도에 대한 이차함수의 형태를 가지게 된다. 또한, 이 문제에서 첫 번째 제약 조건은 변수가 분모에 들어가 있는 형태이므로 이 최적화 문제는 비선형 최적화 문제의 형태를 가지고 있다. 이러한 문제를 직접적으로 접근 하는 것은 상당히 시간이 많이 소요될 수 있으며, 도출된 해가 지역 최적화에 빠질 염려가 있으므로 적절한 방법을 통한 문제의 해결이 요구된다. 본 논문에서는 기하학적 프로그래밍(Geometric programming)을 이용하여 이 속도 계획 문제를 해결하였다.
5.1 기하학적 프로그래밍(Geometric programming)
기하학적 프로그래밍은 비선형 문제들을 로그 변수로 치환시켜 로그 컨벡스(log-convex) 문제로 변환 시켜 푸는 방법이다. 이때, 나오는 로그 컨벡스 문제의 해는 전역 최적해를 보장할 수 있다.(Boyd et.al, 2007) 일반적으로 주어지게 되는 기하학적 프로그래밍의 문제 형태는 다음과 같다.
여기서, 목적함수의 형태는 Posynomial 그리고 부등호 제약 조건의 형태는 Posynomial 마지막으로 등호 제약조건의 형태는 Monomial의 형태를 가진다. Posynomial의 형태는 
의 형태를 가지는 식으로 여기서 계수 aj는 양수이며, 변수 xk 또한 양수 그리고 지수항 bk는 모든 실수가 가능하다. Monomial은 이 Posinomial에서 항이 하나일 때를 뜻한다. 이때 변수에 로그를 취하게 되면 이 최적화 문제는 로그 컨벡스의 형태가 되므로, 우리는 이 최적화 문제를 효율적으로 풀 수 있으며, 이 때 나오게 되는 해는 전역 최적화를 보장할 수 있다.
5.2 속도 계획에 적용
앞서 언급된 것처럼 g(Vi−1,i)는 일반적으로 속력에 대한 이차함수로 표현이 가능하고, 선박의 운항 영역에서는 단순 증가 상태를 보인다. 또한, 해상환경에 의한 선속 저하량 약산식에 따르면, 선속 저하량은 ΔV = Vαμ{(0.7BN + BN6.5) / 2.7▽2/3} /100로 표현이 가능하고, 이미 결정된 항로 위에서 이 값은 선박의 속력에 대한 함수로 표현이 된다. 그러므로, 이 최적화 문제는 다음과 같이 쓰여질 수 있다.
여기서 λi는 1 + αiμi{(0.7BNi + BNi6.5) / 2.7▽2/3} /100이며, λ'i는 λi와 1 / di-1,i의 곱이다. 하지만 위의 최적화 문제에서 바로 기하학적 프로그래밍의 적용은 불가능 하다. 왜냐하면 일반적으로 목적함수의 일차항 C2의 값은 음수 값을 가지는데, 이는 기하학적 프로그래밍의 적용 조건인 목적함수의 형태 Posynomial이 아니기 때문이다. 그러므로 목적함수의 형태를 적절히 변경 시켜야 한다.
● 명제: 어떤 함수가 컨벡스 형태를 가지면, 그 함수는 Posynomial로 근사가 가능하다(Boyd et.al, 2007).
위의 명제에 따라 우리는 목적함수를 Posynomial 형태로 근사를 시켜 기하학적 프로그래밍에 적용이 가능하다.
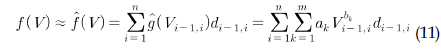
그러므로 이제 변경된 최적화 문제의 형태는 다음과 같이 표현이 가능하다.
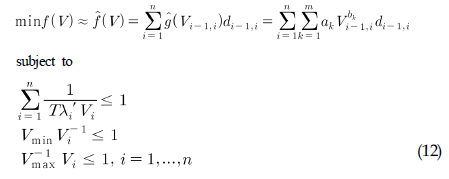
본 논문에서는 CVX TOOL을 이용하여 매트랩(MATLAB)에서 문제를 해결하였다.
6. 시뮬레이션 및 분석
제안된 최적항로 도출법의 실효성을 검증하기 위하여 간단한 시뮬레이션이 수행되었다. 본 논문에서 수행된 시뮬레이션은 동경에서 샌프란시스코까지 가는 8000TEU 급의 컨테이너선을 대상으로 수행 되었으며, 해상환경에 의한 선속의 저하, 그리고 선박의 항해중 안전성 반영을 위하여 ECMWF에서 제공되는 기상 정보 중 유의파고, 파 주기, 파향, 풍속을 획득하였으며, 시뮬레이션을 수행하는 대상 날짜는 2013년 12월 1일부터 8일까지의 총 8일간의 항해를 기준으로 하였다. 일기 정보의 해상도는 위도 경도를 기준으로 하여 1.5도의 그리드 셀을 기준으로 주어지며 정보는 여섯시간 간격으로 업데이트 된다. 대상 선박의 주요 치수를 선박의 길이를 기준으로 하여 무차원화한 값은 다음과 같다.
Nondimensionalized Principal Dimension of Subject Ship
Phase 1에서 수행되는 최적 경로 생성을 위한 그리드는 경도기준 1.5도, 위도기준 0.3도로 하여 선박의 방향각을 좀 더 다양하게 줄 수 있도록 하였다. 이때, 하나의 노드에서 뻗어 나갈 수 있는 노드 연결 가지 수는 아홉개로 설정 하였다. 또한 속도 계획의 유효성을 보기 위하여 엔진 출력을 고정한 항해 시나리오 그리고 선박의 속력을 고정한 시나리오와 연료 소모량 측면에서 비교를 수행하였다. 또한 본 논문에서 시뮬레이션을 위해 사용한 컴퓨터는 i7- 1.7GHz 쿼드 코어 컴퓨터 이며, Matlab을 이용하여 구현하였다. 이를 바탕으로 수행한 시뮬레이션 결과는 다음과 같다.
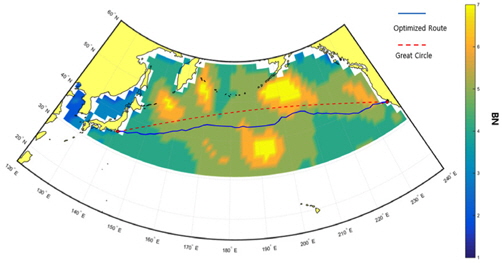
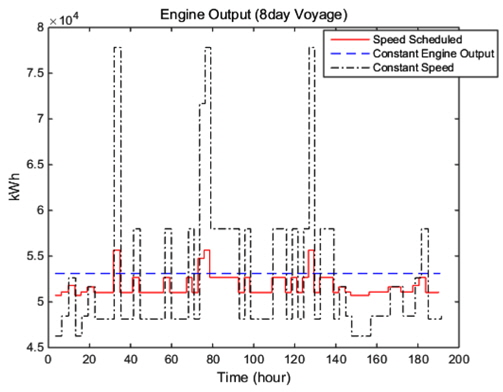
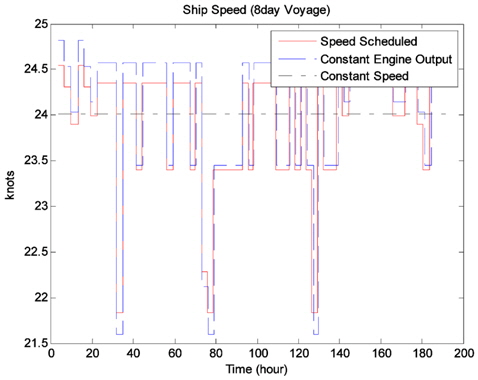
Fig. 2-5은 두 단계의 최적화를 통해 생성된 최적 항로와 이를 운항할 때 각 시간별 선박의 운항 속력 그리고 엔진 출력 또한 같은 시각 대권 항로에서의 속력 감소량을 비교한 것이다. 또한 Table 4는 RTAA* 알고리즘을 통해 형성된 경로에 대한 노드 탐색 수와 기존의 A* 알고리즘을 통한 경로생성에서 노드 탐색 수 그리고 다익스트라 알고리즘을 통할 때 노트 탐색 수를 최초 탐색과 출항 후 여섯시간 후를 비교한 것이다. Table 4에서 제시된 결과를 통해 RTAA* 알고리즘을 통해 최초 경로 생성 이후 두 번째 경로 생성에서 노드 확장 수가 기존의 A* 알고리즘에 비해 줄어들게 되므로 해상 환경이 바뀌었을 때 경로 재생성에서 계산시간을 단축할 수 있음을 알 수 있다. Fig. 5에서 보여주고 있는 대권항로와 최적 항로에서의 해상환경에 의한 속력 감소를 비교하면, RTAA* 알고리즘을 통해 형성된 최적항로의 속력 감소는 전체적으로 대권항로에서의 속력 감소량보다 작음을 알 수 있다. 이를 통해 RTAA* 알고리즘이 최적 경로 생성에 적절한 알고리즘임을 알 수 있다. 또한, Phase 2 에서 속도 최적화를 수행할 때 최초 탐색된 경로에서 소요되는 계산 시간은 동일하게 24.09초였다. 이는 Phase 2에서 크게 차이가 나지 않는 계산 시간을 Phase1에서 사용되는 알고리즘 변경을 통해 계산시간의 효율성을 높일 수 있다는 것을 의미한다. Fig. 3-4에서 항해 후 약 30 시간이후와 80시간 이후에 선박의 속력 저하가 크게 일어남을 알 수 있다. 이것은 Fig. 5에 나오는 속력 감소량과 비교해 보면 당시 해상 환경이 좋지 않았음을 알 수 있다. Fig. 5 의 엔진 출력 결과를 보면, 속도 계획을 통해 도출된 엔진 출력은 속도를 고정한 항해 시나리오의 패턴과 유사함을 알 수 있다. 비슷하게 Fig. 4의 선박의 속도는 엔진 출력을 고정한 항해 시나리오의 패턴과 유사함을 알 수 있다. 이를 통해 선박의 속도 계획 최적화는 각 시각별 속도와 엔진 출력이라는 두 가지 변수에 대해 자유도를 가지게 되고 이에 대한 최적화를 이루어냈다고 판단할 수 있다.
Optimized Route Vs. Great Circle
Time History of Speed Reduction (reference speed : 24knots)
Comparison on Number of Node Expansion & Searching Time
Engine Output
Ship Speed during the Voyage
Phase1에서 수행되는 계산 시간을 비교해 보면 기존 A* 알고리즘에 비해 RTAA* 알고리즘은 노드 확장 수가 두 번째 단계에서 12.7% 감소하는 것을 보이지만 실제 계산 시간은 15.3% 감소하는 것을 알 수 있다. 이는 길찾기 알고리즘의 특성상 데이터의 더미(Stack)가 쌓이게 되면서 일어나는 현상으로, 경로점을 많이 설정하여 최적항로 생성을 할 경우 RTAA* 알고리즘을 통해 계산시간에서 더 좋은 효율을 얻을 수 있을 것으로 기대된다. Table 5에서 알 수 있듯이 경로 최적화를 한 경우(Phase 1)와 대권항로에서 속도를 고정한 항해를 비교하면 항해 거리에서는 최적항로가 287km 더 길었지만 4.6%의 연료 소모 감소를 보였으며 총 운항시간에서도 5.2 시간의 단축을 보였고, 최적화 된 경로에서 속도 최적화를 한 항해의 경우(Phase 2) 대권항로에 비해 8.4%의 연료 소모값 감소를 보였다. 이를 통해 Phase 1에서의 경로 최적화가 적절히 이루어짐을 알 수 있으며 또한 Phase2를 통해 또 한번의 항해 전략의 최적화를 이루어냈다고 판단 할 수 있다.
Comparison on Fuel Consumption
7. 결 론
본 논문에서는 선박의 최적항로 문제를 두 단계로 나누어 해결하는 방법을 제시하였다. 첫번째 단계 Phase 1에서는 선박의 속도를 고정한 후 RTAA* 알고리즘을 통해 경로를 최적화 하였다. RTAA* 알고리즘에서 주어지는 좀 더 좋은 정보의 휴리스틱 값을 통해 길 찾기에서 노드 확장 횟수를 줄여 최적 항로 생성에서 계산 시간을 단축할수 있음을 보였다. Phase 2에서는 비선형 최적화 문제를 기하학적 프로그램으로 변환하여 구간별 속도를 최적화 하였다. 두 번째 단계에서 기하학적 프로그래밍으로 변환을 할 경우 이 최적화 문제는 컨벡스 형태를 지니게 되므로 문제를 효율적으로 해결할 수 있으며 이때 나오는 최적화 해는 전역 최적해를 보장할 수 있다는 장점이 있다. 마지막으로 연료 소모값에서 최적화 된 경로에서 속도 계획은 대권항로에서의 항해와 비교하여 8.4%의 연료 감소 효과를 보일 수 있었다. 본 논문에서 제시된 방법을 통해 최적항로 문제에서 도움을 줄 수 있는 길을 제시할 수 있을 것이다.
Acknowledgements
본 연구는 서울대학교 LRFC에서 지원되는 연구비에 의하여 수행되었음.
References
Boyd, S., Kim, S.J., Vandenberghe, L., Hassibi, A., 2007. A tutorial on geometric programming. Optimization Engineering, 8(1):67–127.
Boyd S., Kim S.J., Vandenberghe L., Hassibi A.. A tutorial on geometric programming. Optimization Engineering 2007;8(1):67–127. 10.1007/s11081-007-9001-7.He-ping, H., 2007. The Development Trend of Green Ship Building Technology. Guangdong Shipbuilding, 3, 002.
He-ping H.. The Development Trend of Green Ship Building Technology. Guangdong Shipbuilding 2007;3:002.Hinnenthal, J., Clauss, G., 2010. Robust Pareto-optimum Routing of Ships utilising Deterministic and Ensemble Weather Forecasts. Ships and Offshore Structure, 5(2), 105–114.
Hinnenthal J., Clauss G.. Robust Pareto-optimum Routing of Ships utilising Deterministic and Ensemble Weather Forecasts. Ships and Offshore Structure 2010;5(2):105–114. 10.1080/17445300903210988.International Maritime Organization (IMO), 2007. Revised Guidance to the Master for Avoiding Dangerous Situations in Adverse Weather and Sea Conditions (MSC/Circ. 1228). International Maritime Organization, London.
Revised Guidance to the Master for Avoiding Dangerous Situations in Adverse Weather and Sea Conditions (MSC/Circ. 1228) International Maritime Organization. London: 2007.Koenig, S., Likhachev, M., 2006. Real-time Adaptive A*. Proceedings of the Fifth International Joint Conference on Autonomous Agents and Multiagent Systems, New York USA, 281-288.
Koenig S., Likhachev M.. Real-time Adaptive A* In : Proceedings of the Fifth International Joint Conference on Autonomous Agents and Multiagent Systems. New York USA; 2006. p. 281–288.Roh, M.I., 2013. Determination of an Economical Shipping Route Considering the Effects of Sea State for Lower Fuel Consumption. International Journal of Naval Architecture and Ocean Engineering, 5(2), 246–262.
Roh M.I.. Determination of an Economical Shipping Route Considering the Effects of Sea State for Lower Fuel Consumption. International Journal of Naval Architecture and Ocean Engineering 2013;5(2):246–262. 10.3744/JNAOE.2013.5.2.246.Russell, S.J., Norvig, P., Canny, J.F., Malik, J.M., Edwards, D.D., 1995. Artificial Intelligence: a Modern Approach (Vol. 2). Prentice Hall, Englewood Cliffs.
Russell S.J., Norvig P., Canny J.F., Malik J.M., Edwards D.D.. Artificial Intelligence: a Modern Approach Prentice Hall. Englewood Cliffs: 1995.Shao, W., Zhou, P., Thong, S.K., 2012. Development of a Novel Forward Dynamic Programming Method for Weather Routing. Journal of Marine Science and Technology, 17(2), 239–251.
Shao W., Zhou P., Thong S.K.. Development of a Novel Forward Dynamic Programming Method for Weather Routing. Journal of Marine Science and Technology 2012;17(2):239–251. 10.1007/s00773-011-0152-z.Townsin, R.L., Kwon, Y.J., 1993. Estimating the Influence of Weather on Ship Performance. Royal Institute of Naval Architecture Trans 134(B), 191–210.
Townsin R.L., Kwon Y.J.. Estimating the Influence of Weather on Ship Performance. Royal Institute of Naval Architecture Trans 1993;134(B):191–210.