대칭 및 비대칭 2차원 쐐기의 입수 충격에 관한 실험적 연구
Experimental Study of Water Impact Loads on Symmetric and Asymmetric Wedges
Article information
Trans Abstract
In the present study, the water impact loads on two-dimensional symmetric and asymmetric wedges were mainly studied. The impact pressure and force were measured during a vertical drop of the symmetric and asymmetric wedges. The measured pressure was compared with analytic solutions. The measured force at a local area of the wedge was compared with the integrated pressures and analytic solutions. Some findings on symmetric and asymmetrical wedge drops are presented, and the reliability of the force sensor used for the measurement of the local impact force is discussed.
1. 서 론
해양구조물 및 선박은 슬래밍(Slamming)에 의하여 좌굴 등의 직접 손상을 받을 수 있으며 충격의 진동으로 인한 피로손상을 받을 수 있다. 따라서 해양구조물 및 선박에 대한 슬래밍 하중은 설계 과정에서 필수적으로 고려되어야 하는 요소이다. 입수 충격 문제는 Von Karman(1929)과 Wagner(1932)에 의해 시작되었고 이후로 수많은 연구 결과들이 발표되었다. 기존의 연구들에서는 여러 선저구배각(Dead-rise angle)을 갖는 2차원 쐐기의 충격 하중이 주로 연구되어 왔다. 쐐기 모형은 형상이 간단하면서도 입수 충격이 발생하는 우주 캡슐, 수상 비행기의 착륙장치나 선박 등의 하부 형상과 비슷하였기 때문에 주로 연구되어 왔다. 2차원 쐐기의 수직낙하와 관련하여 포텐셜 유동에 기반한 다양한 해석해들이 발표되었다(Dobrovol’skaya, 1969; Zhao and Faltinsen, 1993; Zhao et al., 1997; Mei et al., 1999). 이러한 해석해들은 주로 물체의 낙하속도가 입수시에도 일정하다는 가정을 통하여 도출되었다. 해석적 연구 이외에도 포텐셜 유동에 근거한 수치해석 결과들이 발표되었으며, 최근에는 전산유체역학(Computational fluid dynamics)에 기반한 해석 결과들이 발표되고 있다. 실험에 기반한 연구에서는 충격 압력이나 입수에 의한 자유표면의 변화 양상이 주로 연구되었다(Zhao et al., 1997; Yettou et al., 2006; Tveitnes et al., 2008). 최근에는 3차원 원뿔 형상이나 반구 형상에 대한 낙하 실험이 수행되었다(Peseux et al., 2005; Alaoui et al., 2012). 비대칭형 쐐기의 입수 충격과 관련한 연구는 대칭형 쐐기에 관한 연구보다 많지 않다. Judge et al.(2004)은 비대칭형 쐐기가 낙하하는 경우의 유동 박리에 대한 실험 결과를 보여주었다. Semenov and Iafrati (2006)는 입수 속도가 일정하다는 가정하에 비대칭형 쐐기의 입수 충격과 관련한 해석해를 발표하였고 Xu et al.(2008)은 수치적인 결과를 Semenov and Iafrati(2006)의 결과와 비교하였다.
기존의 연구들에서는 입수시에 발생하는 충격압력, 자유표면의 변화 그리고 물체에 작용하는 전체 하중이 주로 연구되었다. 그러나 실제 슬래밍과 관련하여 구조적인 관점에서는 충격압력의 최대 크기보다 국부적으로 분포된 충격힘의 양상과 크기가 중요하다. 하지만 기존의 여러 실험적 연구들에서 국부적인 충격힘을 정확하게 계측하기 위한 연구가 수행된 바가 거의 없으며, 계측된 결과를 해석해나 수치해석 결과와 비교한 결과도 거의 없다. 이에 따라 본 연구에서는 충격압력이 아닌 국부적인 충격힘을 계측하기 위한 실험적 연구를 수행하였다. 이를 위하여 임의의 선저구배각을 갖는 2차원 쐐기 모형을 선정하고 여러 압력계와 힘센서를 배치한 뒤 낙하시에 발생하는 충격압력과 국부적인 충격힘을 계측하였다. 이로부터 계측된 충격압력을 해석해들과 비교하여 실험 결과의 타당성을 검토하고, 계측된 충격힘을 적분된 압력의 결과들과 비교하여 충격힘의 특성을 고찰였다. 그리고 본 연구에서 제시된 충격힘의 계측 방법에 대한 적절성을 논의하였다.
국부적인 충격힘의 계측 이외에도 앞서 언급한 바와같이 비대칭형 쐐기의 낙하시에 발생하는 충격압력이나 하중을 계측한 실험 결과도 많지 않다. 이에 따라서 본 연구에서는 2차원 쐐기에 대하여 여러 기울임각을 적용하여 비대칭형 쐐기의 수직 낙하 실험을 수행하여 그 결과를 고찰하고 비대칭형 쐐기의 낙하 특성에 대하여 고찰하였다.
2. 실험 준비
2.1 실험 모형 및 하중계측 장치
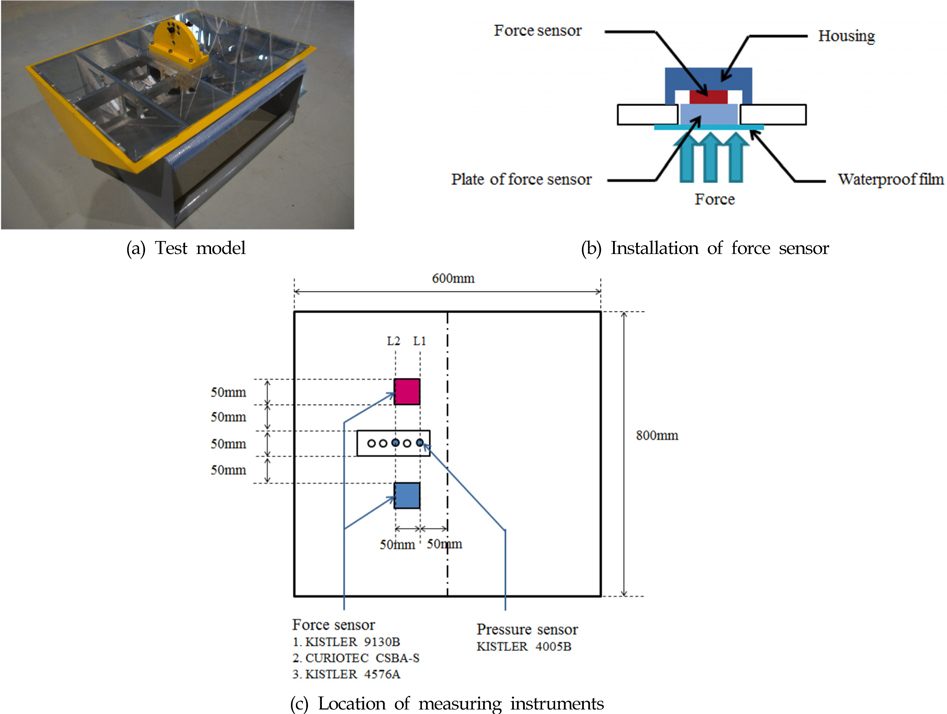
본 실험에서는 선저구배각이 30degree인 2차원 쐐기 모형이 적용되었다. Fig. 1(c)에서 보는 바와 같이 쐐기 모형의 폭(B)과 길이(L)는 각각 600mm, 800mm이다. 쐐기 모형은 충격에 의한 진동을 최소화하기 위하여 16mm 두께의 알루미늄으로 제작하였고 내부에 틀을 제작하였다. 공기 중에서 쐐기 모형에 임의의 충격을 주었을 때 신호를 계측하였고 입수시 계측되는 충격하중의 크기에 비하여 상당히 작은 수준임을 확인하였다. Fig. 1(c)와 같이 두 개의 압력센서를 쐐기 모형의 경사면에 배치하였고 동일한 선상에 서로 다른 세 개의 힘센서를 배치하였다. 힘센서는 Fig. 1(b)에서 보는 바와 같이 두께가 10mm인 덮개 (Housing)에 부착되어 있고 힘센서판(Plate of force sensor)을 통해서 하중을 전달받도록 설치하였다. 힘센서판과 쐐기 모형 사이에는 0.5mm 정도의 유격이 있으며 입수시 유체가 입수될 수 있으므로 방수 필름을 부착하였다. 낙하 실험시 방수 필름을 제거한 경우와 제거하지 않은 경우의 충격힘을 계측하였을 하중의 크기에 큰 차이가 없음을 확인하였다.
Test model and arrangement of measuring instruments
입수 충격힘의 계측과 관련하여 어떠한 힘센서가 적합한지 알려진 바가 없다. 정확한 충격하중의 계측을 위하여 힘센서는 빠른 응답성을 갖으면서도 소음(Noise) 수준이 낮아야 한다. 또한 모형에 부착할 수 있는 크기여야 하며 동일한 충격 하중에 대해 일정한 반복성을 나타내야 한다. 이러한 요소들을 고려하여 두 가지 스트레인게이지 형식(Strain-gauge type)의 센서들과 한 가지 압전형태(Piezoelectric type)의 센서를 적용하였다. 스트레인게이지 형식의 힘센서는 충격하중처럼 빠른 응답을 계측하는 데 많이 적용되지는 않지만, 여러 조선해양공학실험에서 정적 및 동적 하중을 계측하기 위하여 적용되었다. 본 연구의 목적은 힘을 계측하는 것이므로 상대적으로 동적 응답성이 좋은 두 가지 사양의 스트레인게이지 센서를 적용하였다. 압전형태의 센서들은 하중의 크기가 바로 전하량의 차이로 나타나므로 스트레인게이지 형식의 센서들에 비하여 좀더 빠른 응답 특성을 갖는 것으로 알려져 있다. 따라서 적용 가능한 하나의 압전센서를 적용하였다. 센서들의 특성을 Table 1에 나타내었다. 하중을 계측하는 힘센서판의 크기는 가로와 세로를 각각 50mm의 크기로 적용하였다. 본 연구에서 충격압력과 충격힘은 각각 20kHz 및 2kHz로 계측하였다. 본 논문은 특정 센서의 장단점을 보이기 위함이 아니므로 실험 중 계측된 결과는 ‘Force sensor A, B, C’로 나타내었다.
Main features of force and pressure sensors
2.2 낙하실험 장비
낙하속도와 선저구배각은 충격하중의 크기에 영향을 미치는 가장 중요한 요소들이다. 실험에서 낙하속도는 정확하게 계측되어야 하며 선저구배각은 낙하시 충격이 발생하여도 일정하게 유지되는 것이 중요하다. 또한 본 실험은 2차원 실험이므로 입수시에 3차원 유동의 효과가 최소화 되어야 하며 입수 충격에 의한 모형과 계측장비들의 진동도 억제되어야 한다. 추가적으로 비대칭형 쐐기의 낙하실험에서 발생하는 비대칭의 하중에도 쐐기가 회전하지 않도록 하여야 한다. 이러한 요소들을 고려하여 Fig. 2에 나타난 바와 같이 낙하실험 장치를 고안 및 제작하였다.
Drop test facility
우선 3차원 유동에 의한 효과를 최소화 하기 위하여 물막이판(Water blocking panel)을 설치하였다. 쐐기 모형은 물탱크의 벽과 물막이판 사이로 낙하하게 되며 이때 쐐기 모형 앞뒤로 물탱크의 벽과 물막이판 사이에 존재하는 간격은 5mm 이하이다. 수직 낙하속도는 가속도계에서 계측된 가속도를 적분하여 도출하거나, 고속영상촬영 장비에서 촬영된 영상의 변위를 분석하여 도출한다. 가속도는 2kHz로 계측하였고 고속영상촬영은 초당 5000프레임으로 촬영하였다. 쐐기 모형은 공압트리거 장치에 고정되어 있다가 순간적으로 낙하하며 수직으로 설치된 선형운동가이드(Linear motion guide)를 따라 낙하하게 된다. 기존의 실험들에서는 종종 다른 고정장치 없이 자유낙하가 수행되었으나, 이러한 경우 3차원 유동에 의한 영향을 배제하기 어려웠다. 본 실험에서는 3차원 유동을 억제하기 위하여 물막이판과 물탱크 벽을 쐐기 모형에 5mm 이내로 배치하였으나, 이러한 경우 입수시 모형과 충돌 위험이 있었다. 따라서 이를 방지하기 위하여 선형운동가이드를 설치하였다. 선형운동가이드의 적용은 비대칭형 모형의 자유 낙하시 발생할 수 있는 회전을 억제하는데도 효과적이다. 다수의 낙하를 통하여 본 연구에서 고안한 낙하실험 장치가 2차원 모형 낙하실험에 적합함을 확인하였고 비대칭형 모형의 수직낙하에도 모형의 회전을 효과적으로 억제함을 확인하였다.
본 연구에서 낙하 높이는 0.5m로 적용하였다. 낙하높이는 자유표면에서 쐐기 꼭지점까지의 거리를 의미한다. 비대칭형 쐐기의 낙하 실험에는 10, -10, 20 및 -20degree의 기울임각(Tilting angle)을 주었다. 자유표면과 계측센서가 부착된 쐐기의 경사면이 이루는 각도는 선저구배각에서 기울임각을 뺀 각도이며 양의 기울임각일 때 계측센서와 자유표면의 각도가 음의 기울임 각일때보다 더 작아서 큰 충격하중을 받는다.
3. 해석해
대칭형 2차원 쐐기의 낙하와 관련한 다양한 해석해들이 발표되었다. Fig. 3(a)에 나타낸 바와 같이 대표적으로 Dobrovol’skaya (1969)의 상사해(Similarity solution)가 있으며 Zhao et al.(1997)과 Mei et al.(1999)도 Wagner 방법에 기반한 해석해를 발표하였다. 이들의 해석해는 근본적으로 낙하속도가 일정하다는 가정에서 도출되었다. 본 실험에서 계측한 낙하속도를 Fig. 6에 나타내었다. 쐐기의 꼭지점이 물에 닿는 순간(t=0.0sec)부터 모든 센서들이 입수되는 순간(t=0.011sec)까지 속도변화를 보면 일정한 속도는 아니지만 그 변화량이 크지 않다고 가정할 수 있다. 이를 바탕으로 해석해와 실험의 계측결과를 비교해 볼 수 있다. Fig. 3의 해석해에 식 (1)과 같이 실험에서 계측된 매 순간의 낙하속도 (V(t))를 고려하여 Fig. 4(a)와 같은 압력(P)의 시간 이력을 나타낼수 있다.
Anaytic solutions of symmetric and asymmetric wedges
Comparison of drop velocity evaluated from the vertical acceleration and displacement (dead-rise angle = 30deg., drop height = 0.5m, tilting angle = 0deg.)
Analytic solutions of impact pressure and force evaluated by the measured velocity (dead-rise angle = 30deg., drop height = 0.5m, tilting angle = 0deg.)
P는 물의 밀도, Cp는 압력계수이다. 낙하실험에서 계측한 압력을 매 순간의 낙하속도로 무차원화하는 식 (1)은 Zhao et al.(1997)에 나타나 있으며 Yettou et al.(2006)은 자유 낙하시 계측된 충격압의 최대 크기를 식 (1)로 나타내었을 때 Mei et al.(1999)의 해석해와 잘 일치한다는 결과를 보여주었다. Fig. 4(a)와 같이 충격힘이 계측되는 면적에 대하여 분포하는 충격압력을 알 수 있고, 매시간마다 이를 적분하면 Fig. 4(b)와 같이 충격힘의 시간 이력을 구할 수 있다. 자유낙하하는 물체의 대하여 다음 식에서 보는 것과 같이 부가질량(ma)의 시간변화량 외에도 가속도(dV / dt)에 비례하는 부가질량의 항이 충격하중으로 작용한다(Fairlie-Clarke and Tveitnes, 2008).
식 (2)의 두번째 항은 물체의 낙하속도가 변화하는 경우에 고려되어야 하는 항으로 실제의 입수 문제에서 고려되어야 하는 성분이다. 일반적으로 이 성분은 충격 압력의 최대 크기에는 큰영향을 주지 않는 것으로 알려져 있으나 충격힘을 추산할 때 고려되는 성분이다. Fig. 4(b)에 나타난 충격힘은 식 (2)의 두번째 항이 고려되지 않은 항이다. 쐐기의 부가질량은 해석적으로 쉽게 구할 수 있고 계측된 가속도를 곱하면 식 (2)의 두번째 항을 계산할 수 있다. 그러나 본 연구에서 비교하고자 하는 충격힘은 쐐기에 국부적으로 작용하는 하중이며 쐐기의 국부적인 부가질량을 유도하기가 쉽지 않다. 따라서 이를 정확하게 비교하기는 쉽지 않다.
서론에 언급한 바와 같이 비대칭형 쐐기의 낙하에 대한 실험적, 해석적 연구는 많지 않다. 최근에 들어서야 Semenov and Iafrati(2006)가 Fig. 3(b)과 같이 비대칭형 쐐기의 수직 낙하에 대한 해석해를 제안하였다. 이들의 결과도 쐐기가 일정한 속도로 낙하한다는 가정하에 유도되었다. Semenov and Iafrati (2006)의 결과도 대칭형 쐐기의 해석해와 같은 과정을 거쳐 시간 이력으로 도출되었고 계측된 실험결과와의 비교에 사용되었다.
4. 모형시험 결과 및 해석
4.1 낙하 속도
Fig. 5에 기울임각이 0degree인 쐐기가 0.5m에서 낙하하는 모습을 나타내었다. 쐐기가 물에 입수하는 순간부터 모든 센서들이 입수하게 되는 시간은 0.011sec이다. 쐐기의 삼각면 꼭지점 부근에 붙어있는 표식의 위치를 분석하여 쐐기가 낙하하는 변위를 구할 수 있으며 이를 미분하여 낙하속도를 구할 수 있다.
Snapshot of water-entry of wedge from the initial entry (dead-rise angle = 30deg., drop height = 0.5m, tilting angle = 0deg.)
Fig. 6에 계측된 가속도를 적분하여 구한 낙하속도와 고속촬영영상의 변위로부터 구한 낙하속도를 비교하여 나타내었다. 낙하높이가 0.5m인 경우에 쐐기가 입수를 시작할 때의 이상적인 낙하속도는 3.13m/s이며 본 실험에서 계측된 낙하속도는 입 수 초기에 3m/s보다 좀더 큰 속도를 보여준다. 계측된 결과가 좀더 작은 것은 선형운동가이드에서 발생하는 마찰이 가장 큰 이유라고 볼 수 있으나 3% 정도의 속도 감소는 무시할만한 수준이라고 보여진다. 입수 후 낙하속도는 바로 감소되지 않고 일정시간 증가하게 되는데 이는 이 시간동안 쐐기의 무게가 충격력과 부력과 같은 상방향 힘의 합보다 크기 때문이다. 낙하속도의 감속은 상방향 힘이 무게보다 커지는 t=0.01sec 부근에서부터 시작한다. 10회 이상의 낙하 시험에서 계측된 낙하속도가 동일한 반복성을 보여주었다. 고속촬영영상으로부터 구한 낙하속도는 큰 진동이 나타나는데 이는 쐐기가 입수되면서 발생한 유동이 변위 계측을 위해 부착한 표식을 지나면서 발생한 영상분석 상의 소음이다. 또한 작은 진동은 변위를 작은 시간간격으로 미분하면서 발생한 소음이다.
4.2 계측된 압력과 해석해의 비교
대칭형 쐐기에 대한 낙하 실험에서 계측된 압력의 시간 이력을 Fig. 7에 나타내었고 이를 해석해에서 유도된 결과와 비교하였다. Fig. 8에서는 충격압력의 최대크기만을 비교하였다. L1에서 계측된 압력의 최대 크기는 해석해의 결과와 유사한 크기를 보여주는데 비하여 L2에서 계측된 압력은 해석해의 결과보다 다소 작게 나타난다. 또한 L1 및 L2에서 공통적으로 계측된 압력과 해석해에 있어서 최대 압력 이후에 나타나는 압력의 크기에 차이가 있다. Zhao et al.(1997)도 쐐기의 입수가 진행될수록 수치해석 결과와 실험 결과에 차이가 발생함을 보여주었고 3차원 효과의 발생이 이러한 차이를 크게 할 수 있다고 언급하였다. 본 실험에서는 이러한 차이의 가장 큰 이유가 해석해에서 가정하는 일정한 낙하속도 때문이라고 보여진다. 해석해는 가속도가 없다는 가정으로 유도되지만 실제 실험에서는 입수중에 가속도가 지속적으로 변화하며 입수가 진행될수록 가속도와 부가질량에 비례하는 항이 커질 수 있기 때문이다.
Measured pressure at L1 and L2 (dead-rise angle = 30deg., drop height = 0.5m, tilting angle = 0deg.)
Comparison of peak pressure (dead-rise angle = 30deg., drop height = 0.5m, tilting angle = 0deg.)
압력이 발생하는 시간부터 최대 압력이 발생하는 시간까지를 상승 시간(Rise time)으로 정의할 수 있으며 이는 충격압력의 최대 크기와 함께 충격압력의 특징을 나타내는 요소이다. 실험에서 계측된 충격압력의 상승시간은 Dobrobol’skaya(1969)의 상사해가 다른 해석해들보다 가장 근사한 경향을 보여주었다.
4.3 계측된 힘과 압력 적분값의 비교
충격힘은 계측된 압력이나 해석해의 압력을 적분하여 구할 수 있다. Fig. 9에 힘센서로 계측된 충격힘의 시간이력과 적분된 압력 결과들을 비교하여 나타내었다. 실제의 충격 압력은 L1에서 L2의 위치로 가면서 최대 크기나 형상이 변화한다. 본 연구에서는 L1에서 계측한 충격압력의 형상이 있을 때 이러한 충격압력의 형상이 L2까지 진행된다고 가정하고 이를 적분하여 국부적으로 작용하는 충격힘의 시간이력을 계산하였다. 또한 이와 마찬가지로 L2에서 계측한 충격압력의 형상이 L1에서부터 L2까지 진행된다고 가정하고 이를 적분하여 충격힘의 시간이력을 계산하였다. 따라서 실제로 작용한 충격힘은 L1의 압력으로 부터 적분된 힘이나 L2의 압력으로부터 적분된 힘과 근사한 경향을 보여야 한다. Fig. 9에는 세가지의 다른 힘센서 중에서 계측된 하나의 신호를 비교하여 나타내었으며 적분된 압력과 꽤 유사한 경향을 보여주는 것을 알 수 있다.
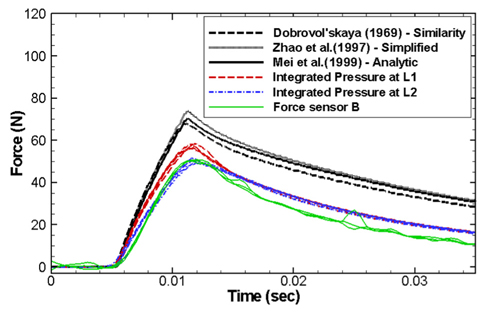
Comparison of measured force and analytical solution (dead-rise angle = 30deg., drop height = 0.5m, tilting angle = 0deg.)
Fig. 7(a)에서 보는 바와 같이 L1에서 계측된 압력의 최대 크기는 해석해의 결과와 거의 유사하지만 최대 충격압 이후의 압력 크기에 차이가 있었다. Fig. 7(a)와 (b)에서 L1과 L2에서 계측된 충격압력을 비교해보면 압력의 최대 크기 차이가 있으나 이후의 압력 크기는 비슷해보인다. Fig. 9에서 이들을 적분한 결과를 비교해보면 해석해는 L1 및 L2에서 적분된 압력과 차이가 크며 L1와 L2에서 적분된 압력의 차이는 상대적으로 작아보인다. 이로부터 최대 충격압의 크기보다 최대 충격압 이후에 나타나는 압력의 크기가 충격힘의 도출에 더욱 중요한 영향을 주는 것을 알 수 있다. 결론적으로 구조적인 강도평가 관점에서 충격하중을 고려하는 경우에 충격 압력의 최대 크기보다 충격 압력의 전반적인 크기와 지속시간을 정확히 고려하는 것이 중요하다고 할 수 있다. 해석해와 계측된 압력에서 최대 충격압 이후에 나타나는 압력의 차이는 앞서 언급한 바와 같이 가속도와 관련한 항이 주요한 원인으로 작용하였을 수 있으며 정확한 비교를 위해서는 이를 반영하는 것이 필요하나 하중을 계측하는 영역에만 국부적으로 작용하는 부가질량의 산정이 어려워 본 연구에서는 이를 나타내지 않았다.
Fig. 10에 각기 다른 세개의 힘센서에서 계측된 최대 충격힘의 크기를 나타내었다. 세개의 센서가 계측된 압력을 적분한 결과에 근사한 최대 충격힘을 보여주며 Force sensor C가 가장 유사한 경향을 보여주고 있다. 해석해로부터 계산한 결과는 계측된 힘이나 적분된 압력보다 큰 경향을 보여주고 있으나 그 차이가 크지 않아서 실용적인 관점에서 적용이 가능한 것으로 보여진다.
Comparison of peak force (dead-rise angle = 30deg., drop height = 0.5m, tilting angle = 0deg.)
4.4 비대칭 쐐기에 대한 실험 결과
비대칭 쐐기에 대한 연구 결과는 많지 않다. 대칭형 쐐기 낙하에서는 쐐기의 좌우로 유동이 대칭적으로 발생한다고 가정하여 해석을 수행할 수 있으나, 비대칭 쐐기의 경우에는 쐐기의 좌우로 발생하는 유동의 형태가 다르며 엄밀하게 좌우에 발생하는 유동간의 상호 영향을 실제와 유사하게 가정하기가 쉽지않다. 실험에 있어서도 자유낙하의 경우에는 입수시 발생하는 비대칭 충격하중 때문에 일정한 선저구배각을 유지하는 것이 어렵다. 본 장에서는 비대칭 쐐기를 낙하하며 계측한 충격압력과 충격힘의 결과를 나타내고 이를 해석해와 비교 및 고찰하였다.
다양한 기울임각의 낙하시 계측된 낙하속도를 Fig. 11에 나타내었다. 이때 쐐기는 0.5m에서 낙하되었으며 입수하는 순간부터의 속도를 나타내었다. 기울임각이 10degree 또는 -10degree에서 유사한 경향이 나타나고 20degree 또는 -20degree에서 유사한 경향이 나타나고 있어 좌우의 기울임 각도와 관계없이 동일한 낙하가 수행된 것을 알 수 있다. 기울임각이 더 큰 경우에 입수 후반의 낙하속도가 빨리 감소하는데 이는 자유표면과 쐐기가 이루는 각도가 더 작아서 충격하중이 더욱 크게 발생하기 때문이다.
Enlarged time histories of drop velocity with various tinting angles (dead-rise angle = 30deg., drop height = 0.5m)
기울임각이 10degree와 20degree인 경우의 낙하 모습을 Fig. 12와 13에 나타내었다. 20degree인 경우에 더 짧은 시간동안 쐐기의 많은 부분이 입수하는 것을 알 수 있다. 이는 기울임각이 클수록 더욱 짧은 시간에 계측센서들이 입수하게 되는 것을 의미하며 입수된 부분의 부가질량 변화량이 커지므로 충격하중도 더 커지게 되는 것을 의미한다.
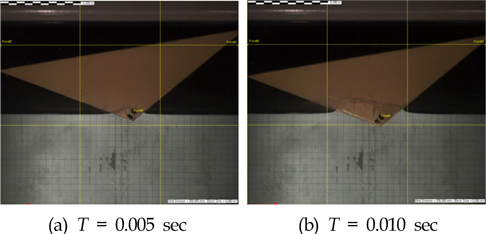
Snapshot of water-entry of wedge from the initial contact (dead-rise angle = 30deg., drop height = 0.5m, tilting angle = 10deg.)
Snapshot of water-entry of wedge from the initial entry (dead-rise angle = 30deg., drop height = 0.5m, tilting angle = 20deg.)
낙하시 계측된 압력을 Fig. 14에 나타내었다. 여기서 Semenov and Iafrati(2006)의 결과는 매 순간의 계측된 낙하속도가 아닌 일정한 낙하속도 3.08m/s를 적용하여 유도하였다. 결과를 보면 계측된 결과와 해석해에 있어서 최대 크기에 차이가 있음을 알수 있고 이러한 차이는 L2에서 더욱 크게 나타나고 있다. 또한 기울임각이 양인 경우에 L1에서 계측된 압력과 해석해는 거의 유사한 시간에 충격압이 발생하였으나 L2에서는 계측된 압력과 해석해 사이에 시간지연이 있는 것을 알 수 있다.
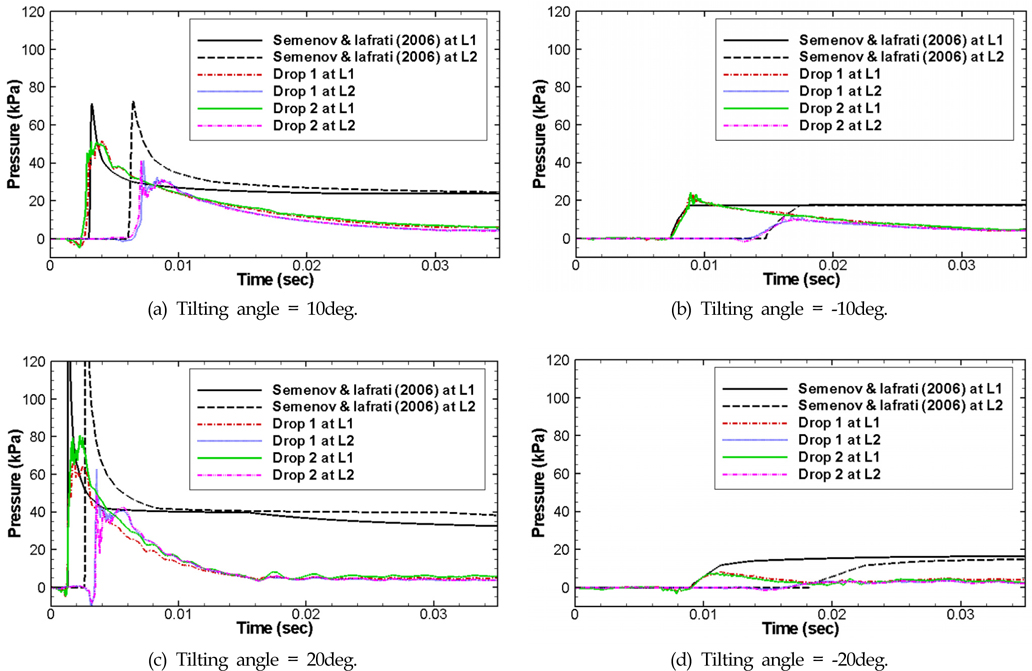
Time histories of pressure with various tilting angles (dead-rise angle = 30deg., drop height = 0.5m)
적분된 압력과 계측한 힘을 Fig. 15에 비교하여 나타내었다. L1와 L2에서 계측된 압력을 바탕으로 적분한 힘은 대칭형 쐐기에서 나타났던 차이보다 더욱 크게 나타났다. 이는 대칭형 쐐기의 실험에서보다 L1에서 L2 지점으로 옮겨가면서 압력이 더욱 급격히 변화하는 것을 의미한다. 힘센서로 계측한 힘은 두 지점에서 계측한 압력들을 적분한 힘의 평균과 유사한 경향을 보여 주어 계측된 힘과 압력의 관계는 타당한 것으로 보여진다. 해석해의 결과는 압력의 결과와 마찬가지로 계측된 결과보다 큰 경향을 보여주며 대칭형 쐐기의 낙하에서보다 그 차이가 큰 것처럼 보인다. 비대칭형 쐐기에서는 낙하속도가 더욱 급격히 변화하기 때문에 대칭형 쐐기의 경우보다 가속도에 의한 영향이 크게 나타날 수 있다. 또한 해석해에서 유도된 결과가 대칭형 쐐기의 경우보다 실제의 유동 효과를 가정하는 데 차이가 발생하였을 수도 있다. 따라서 비대칭형 쐐기의 낙하와 관련하여 좀더 현실적인 해석해가 연구되거나 전산유체역학 등에 기반한 수치적인 해석 결과가 제시될 필요가 있다.
Time histories of force with various tilting angles (dead-rise angle = 30deg., drop height = 0.5m)
5. 결 론
본 논문에서는 2차원 대칭형 및 비대칭형 쐐기에 대한 낙하실험을 수행하였다. 쐐기의 경사면에 압력센서와 힘센서를 분포하여 충격압력과 국부적인 충격힘을 계측하였다. 계측된 압력과 해석해를 비교하였고 적분된 계측된 힘과 적분된 압력 및 해석해를 비교하였다. 대칭형 쐐기와 비대칭형 쐐기의 낙하실험 결과로부터 다음의 결론을 얻을 수 있다.
(1) 최대 충격압의 크기보다 최대 충격압 이후에 나타나는 압력의 크기가 충격힘의 도출에 더욱 중요한 영향을 주는 것을 낙하실험을 통하여 검증하였다. 결론적으로 구조 강도평가시 충격힘을 추산하는 경우에 충격 압력의 최대 크기보다 충격 압력의 전반적인 크기와 지속시간을 정확히 반영하는 것이 중요하다.
(2) 대칭형 쐐기의 낙하와 관련하여 낙하속도가 일정하다는 가정에서 유도된 해석해들은 자유낙하하는 경우의 실험 결과보다 큰 결과를 주었다. 자유낙하의 경우에는 선저구배각이 작아질수록 충격량이 커지며 입수시에 입수속도가 크게 작아질 수있으나 위의 해석해의 경우에는 이러한 영향이 고려되지 않았다. 따라서 낙하속도가 일정하다는 가정에 기반한 해석해는 선저구배각이 작아질수록 자유낙하에 의한 실험결과보다 더욱 큰 결과를 줄 수 있다.
(3) 비대칭형 쐐기 낙하의 경우에 쐐기 경사면의 높이에 따른 충격압력의 크기와 형상은 대칭형 쐐기 낙하의 경우보다 더욱 많이 변화하였고 이는 해석해와 비교하여 큰 차이를 보여주었다. 따라서 비대칭형 쐐기와 관련하여 속도변화가 고려된 더욱 현실적인 결과들이 제시될 필요가 있다.
(4) 낙하실험시에 선형운동가이드의 적용은 가이드에서 발생하는 마찰로 인하여 고정장치 없는 자유낙하에 비하여 낙하속도가 좀더 작을 수 있다. 그러나 선형운동가이드는 비대칭형 물체의 입수시에 발생할 수 있는 회전을 억제할 수 있고, 물체낙하의 수직성을 보장하여 3차원 유동 효과를 억제하는 격벽을 설치하는데도 유리하다.
Acknowledgements
본 연구는 Wave Induced Loads on Ships Joint Industry Project III(PIS7230)에서 수행된 연구결과 중 일부임을 밝히며 American Bureau of Shipping, Bureau Veritas, Germanischer Lloyd, Korean Register of Shipping, Lloyd’s Register, Class NK, 서울대학교와 삼성중공업의 연구비 지원에 감사드립니다. 또한 실험장비 및 모형 설치와 관련하여 도움을 주신 최성권 선임기술원(선박해양플랜트연구소 근무)께 감사드립니다.
References
Alaoui, A.E.M., Nême, A., Tassin, A., Jacques, N., 2012. Experimental Study of Coefficients during Vertical Water Entry of Axisymmetric Rigid Shapes at Constant Speeds. Applied Ocean Research, 37, 183-197.
Alaoui A.E.M, Nême A, Tassin A, Jacques N. Experimental Study of Coefficients during Vertical Water Entry of Axisymmetric Rigid Shapes at Constant Speeds. Applied Ocean Research 372012;:183–197. 10.1016/j.apor.2012.05.007.Dobrovol’skaya, Z.N., 1969. On Some Problems of Similarity Flow of Fluid with a Free Surface. Journal of Fluid Mechanics, 36, 805-829.
Dobrovol’skaya Z.N. On Some Problems of Similarity Flow of Fluid with a Free Surface. Journal of Fluid Mechanics 361969;:805–829. 10.1017/S0022112069001996.Fairlie-Clarke, A.C., Tveitnes, T., 20008. Momentum and Gravity Effects during the Constant Velocity Water Entry of Wedge-Shaped Sections. Ocean Engineering, 35, 706-716.
Fairlie-Clarke A.C, Tveitnes T. Momentum and Gravity Effects during the Constant Velocity Water Entry of Wedge-Shaped Sections. Ocean Engineering 352008;:706–716. 10.1016/j.oceaneng.2006.11.011.Judge, C., Troesch, A., Perlin, M., 2004. Initial Water Impact of a Wedge at Vertical and Oblique Angles. Journal of Engineering Mathematics, 48, 279-303.
Judge C, Troesch A, Perlin M. Initial Water Impact of a Wedge at Vertical and Oblique Angles. Journal of Engineering Mathematics 482004;:279–303. 10.1023/B:engi.0000018187.33001.e1.Mei, X., Liu, Y., Yue, D.K.P., 1999. On the Water Impact of General Two-dimensional Sections. Applied Ocean Research, 21, 1-15.
Mei X, Liu Y, Yue D.K.P. On the Water Impact of General Two-dimensional Sections. Applied Ocean Research 211999;:1–15. 10.1016/S0141-1187(98)00034-0.Peseux, B., Gornet, L., Donguy, B., 2005. Hydrodynamic Impact: Numerical and Experimental Investigations. Journal of Fluid and Structures, 21, 277-303.
Peseux B, Gornet L, Donguy B. Hydrodynamic Impact: Numerical and Experimental Investigations. Journal of Fluid and Structures 212005;:277–303. 10.1016/j.jfluidstructs.2005.04.011.Semenov, Y.A., Iafrati, A., 2006. On the Nonlinear Water Entry Problem of Asymmetric Wedges. Journal of Fluid Mechanics, 547, 231-256.
Semenov Y.A, Iafrati A. On the Nonlinear Water Entry Problem of Asymmetric Wedges. Journal of Fluid Mechanics 5472006;:231–256. 10.1017/S0022112005007329.Tveitnes, T., Fairlie-Clarke, A.C., Varyani, K., 2008. An Experimental Investigation into the Constant Velocity Water Entry of Wedge-shaped Sections. Ocean Engineering, 35, 1463-1478.
Tveitnes T, Fairlie-Clarke A.C, Varyani K. An Experimental Investigation into the Constant Velocity Water Entry of Wedge-shaped Sections. Ocean Engineering 352008;:1463–1478. 10.1016/j.oceaneng.2008.06.012.Von Karman, T., 1929. The Impact on Seaplance during Landing. NACA Technical Note No. 321.
Von Karman T. The Impact on Seaplance during Landing. 1929.Wagner, H., 1932. Über Stoss und Gleitvorgänge an der Oberfläche von Flüssigkeiten. Zeitschrift fur Angewandte Mathematik und Mechanik, 12(4), 193-235.
Wagner H. Über Stoss und Gleitvorgänge an der Oberfläche von Flüssigkeiten. Zeitschrift fur Angewandte Mathematik und Mechanik 12(4)1932;:193–235. 10.1002/zamm.19320120402.Yettou, E.M., Desrochers, A., Champoux, Y., 2006. Experimental Study on the Water Impact of a Symmetrical Wedge. Fluid Dynamic Research, 38, 47-66.
Yettou E.M, Desrochers A, Champoux Y. Experimental Study on the Water Impact of a Symmetrical Wedge. Fluid Dynamic Research 382006;:47–66. 10.1016/j.fluiddyn.2005.09.003.Xu, G.D., Duan, W.Y., Wu, G.X., 2008. Numerical Simulation of Oblique Water Entry of an Asymmetrical Wedge. Ocean Engineering, 35, 1597-1603.
Xu G.D, Duan W.Y, Wu G.X. Numerical Simulation of Oblique Water Entry of an Asymmetrical Wedge. Ocean Engineering 352008;:1597–1603. 10.1016/j.oceaneng.2008.08.002.Zhao, R., Faltinsen, O.M., 1993. Water Entry of Twodimensional Bodies. Journal of Fluid Mechanics, 246, 593-612.
Zhao R, Faltinsen O.M. Water Entry of Twodimensional Bodies. Journal of Fluid Mechanics 2461993;:593–612. 10.1017/S002211209300028X.Zhao, R., Faltinsen, O.M., Aarsnes, J., 1997. Water Entry of Arbitrary Two-Dimensional Sections with and Without Flow Separation. 21st Symposium on Naval Hydrodynamics, Washington DC, USA.
Zhao R, Faltinsen O.M, Aarsnes J. Water Entry of Arbitrary Two-Dimensional Sections with and Without Flow Separation In : 21st Symposium on Naval Hydrodynamics; 1997.