직렬 배치된 두 부유체에 작용하는 조류력 및 풍력 특성에 관한 수치해석 연구
Numerical Study of Current and Wind Forces Acting on Two Floating Bodies in Tandem Configuration
Article information
Trans Abstract
In this study, the characteristics of the current and wind forces acting on two floating bodies were numerically investigated using a commercial CFD software, STAR-CCM+. In the numerical analyses, LNGC was located right behind FSRU under uniform current or wind conditions. Steady calculations were carried out using a Reynolds averaged Navier-Stokes (RANS) solver and the realized k-epsilon model. First, the current coefficients of FSRU based only the CFD were compared with the model test data. Through this comparison, the present numerical models and mesh systems were indirectly verified. Next, computations for FSRU and LNGC in a uniform current were performed using different relative positions. It was found that the current coefficients were great affected by the longitudinal positions. Finally, the wind forces acting on FSRU and LNGC in tandem configurations were studied. The focus was on the shielding effects due to the aerodynamic interactions between FSRU and LNGC.
1. 서 론
부유식 해양구조물은 단일 부유체로 해상 작업을 수행하기도 하지만 석유 또는 천연가스를 운반하는 셔틀탱커나 LNGC(Liquefied natural gas carrier)와 함께 해상 작업을 수행한다. 이러한 구조물의 작업성 확보를 위해서는 설치해역의 환경외력에 대한 거동 특성을 파악하는 것이 중요하며, 이를 위해서는 환경외력(바람, 조류, 파도)을 고려한 해석이 필수적으로 수행되어야 한다. 환경외력의 정확한 계산은 선박이나 부유식 해양구조물의 위치유지 및 안정성 확보 문제에서 필수적인 요소이다. 직렬 또는 병렬 계류된 두 부유체는 서로간의 유체력 간섭 효과가 발생한다. 직렬 또는 병렬 배치된 부유체 각각에 작용하는 환경 외력은 유체력 간섭에 의해 단일 부유체에 작용하는 환경외력과 차이가 발생하는데 이러한 변화가 생기는 현상을 그림자효과(Shielding effect)라한다. 환경외력을 평가하는 방법으로는 경험식을 이용한 추정, 모형시험 및 CFD(Computational fluid dynamics) 수치해석 등이 있다. 최근 전산기기 및 수치시뮬레이션 기법의 발달로 CFD 계산은 계산 시간 및 정도가 향상되어 왔으며, 산업계 및 학계에서 CFD를 이용한 관련연구도 활발히 진행되고 있다.
대표적인 선행연구로 Koo et al.(2004)은 선박의 횡 방향 이격거리에 따른 Wind shielding effect를 검토하여 쉴딩계수(Shielding factor)를 산정하였고, Yuck et al.(2007)은 병렬 계류된 두 선박의 조류력 특성을 실험하였다.
Koop et al.(2010)은 CFD 계산과 풍동실험을 비교하여 직렬 배치된 두 부유체에 작용하는 풍하중을 분석하였으며, Tannuri et al.(2010)은 DP(Dynamic positioning) 시스템이 적용된 셔틀탱커에 작용하는 Wind shielding effect를 CFD를 이용하여 계산하였다. Souza and Ragazzo.(2006)은 직렬배치시 유체력 간섭에 대해 연구하였다. Yuck et al.(2006)는 부유체에 작용하는 조류력을 상용코드인 Fluent를 사용하여 계산하였으며 모형실험, OCIMF(Oil companies international marine forum) 자료와 비교 분석하였다. Tabaczek et al.(2007)은 선수형상에 따른 바지선의 저항특성을 Fluent를 사용하여 비교하였다. Jun et al.(2012)은 상용코드인 STAR-CCM+를 사용하여 KCS(KRISO container ship)선형에 대한 선체주위의 유동해석을 비정렬격자를 이용하여 수행하였다. Park et al.(2012)은 다관절 해저로봇에 작용하는 조류하중 산정 및 유동해석을 수행하였다.
본 연구에서는 부유식 해양구조물인 FSRU(Floating storage and regasification unit)와 LNGC가 직렬배치 되었을 때 조류력 및 풍력 특성을 CFD를 이용하여 수치적으로 살펴보고자 하였다. 먼저 FSRU단독에 대한 조류력 계산을 해양공학수조 모형시험 결과와 비교하여, 수치모델 및 격자계에 대한 검증을 수행하였다. 이 후 직렬배치 된 FSRU와 LNGC에 대해서 일정한 조류 및 바람 조건하에서 유동장 및 항력계수 계산을 수행하였다. 직렬배치 된 두 부유체의 이격거리를 변화시켜 가면서 조류력 및 풍력 특성 변화를 살펴보았으며, FSRU에 의한 그림자 효과의 영향으로 LNGC의 항력 특성이 어떻게 변화하는 지를 살펴보고자하였다.
2. 계산조건 및 문제의 정의
본 연구에서는 상용프로그램인 STAR-CCM+를 사용하여 수치해석을 수행하였다. 형상주위의 유동해석을 위해 난류 유동의 지배방정식인 연속방정식과 운동량 방정식을 포함한 Reynolds-averaged navier-stokes(RANS) 방정식을 사용하고, 난류모델은 K-Epsilon을 사용하였으며, y+에 따라 Wall function을 변화시켜 적용하는 Two-layer all y+ wall treatment 법을 사용하였다. 수치격자는 Trimmer 격자를 사용하여 생성하였다.
수치해석의 진행과정을 간략히 살펴보면 다음과 같다.
(1) 수치계산의 검증을 위하여 모형시험과 동일한 조건으로 계산을 하여 비교 검증을 수행한다.
(2) 단독 부유체의 수치계산을 실선크기로 수행하고 비교 검토한다.
(3) 조류가 있는 환경조건에서 두 부유체를 직렬배치(Tandem)하여 수치계산하고 유동특성을 파악한다.
(4) 바람이 있는 환경조건에서 두 부유체를 직렬배치(Tandem)하여 수치계산하고 유동특성을 파악한다.
직렬배치(Tandem)된 모형의 격자구성을 Fig.2에 각각의 모형에 대한 제원을 Table.1에 나타내었다.
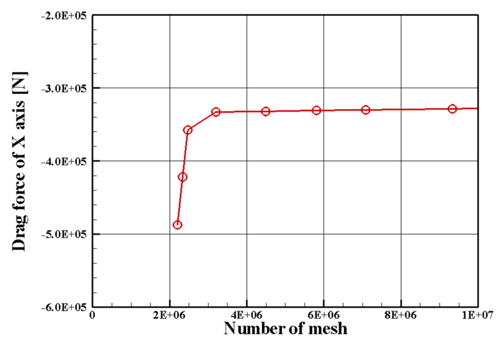
수치계산을 수행하는데 소요되는 시간을 최적화 하고, 격자계의 효율성을 높이고자 격자 의존성(Grid Dependency)에 대해 수치계산 하였다. Fig. 3에서와 같이 기본 격자의 숫자를 200만개부터 1000만개까지 분포하여 테스트해본결과 FSRU 및 LNGC 단독성능 계산의 경우 300만개에서 계산결과가 수렴됨을 확인할 수 있었다.
3. 수치해석 결과
3.1 단독선체
모형시험은 FSRU에 대한 1:60의 축척모형을 이용하여 한국해양과학기술원 선박해양플랜트연구소 해양공학수조에서 수행되었다. 조류 속도는 1.029m/s(2knots)를 고려하였으며, 입사각은 0°~180°까지 15° 간격으로 계측하였다. 수치계산은 모형시험 조건으로 수행하였으며, FSRU의 수선면 아래 부분에 대해서 격자를 생성하여 Steady 계산을 수행하였다. 수치계산에 사용된 격자 수는 약 300만개이며, 유체장의 크기는 입사각 0° 일 때 길이 33m, 폭 10m, 깊이 7.2m이며, 입사각에 따라서 유체장의 길이 및 폭의 변화를 주었다.
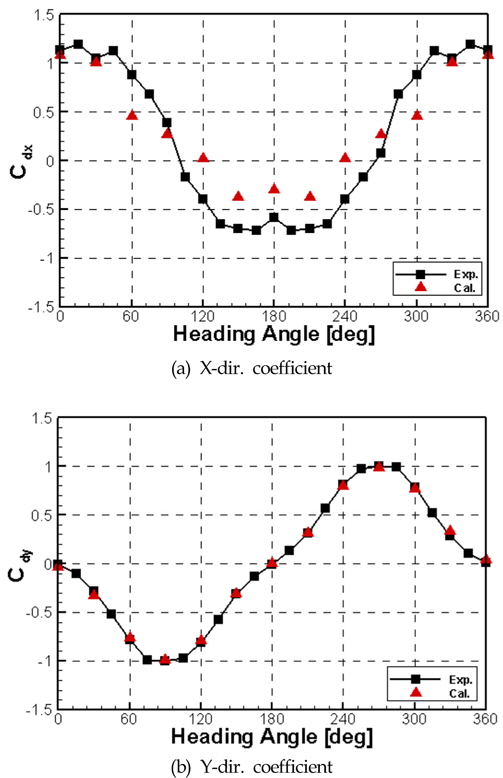
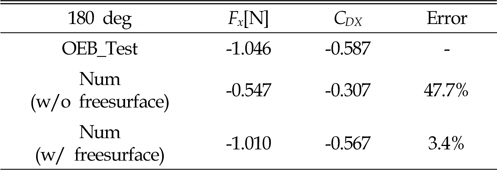
모형시험과 수치계산으로부터 얻어진 조류력 계수를 Fig. 4에 비교하여 도시하고 있다. 현 수치계산에 의한 조류력 계수는 X방향과 Y방향 모두 모형시험 결과와 유사한 경향을 보여주고 있으며, 특히 Y방향 조류력 계수는 모형시험 결과와 매우 잘 일치함을 알 수 있다. 다만, X방향의 조류력 계수 중 선수쪽으로 입사하는 경우에 현 수치계산이 모형시험 보다 더 작은 값을 보여주고 있다. 이러한 오차는 선수부의 자유수면 상승에 의한 항력 증가가 모형시험의 X방향 조류력 계수를 상대적으로 크게 증가시켰기 때문으로 판단되며 입사각이 0deg의 경우에는 FSRU 선미부의 각진 영향으로 자유수면 상승으로 인한 조류력 증가가 상대적으로 작은 것으로 판단된다. 또한 선미부의 각진형상으로 형상 좌우 끝부분의 와류현상으로인한 압력감소가 자유수면효과를 작게 가져오는 효과를 나타내는 것으로 판단된다. Table 2는 입사각 180도 일 때의 자유수면 유무에 따른 조류력 계수를 비교하여 보여주고 있다. 자유수면을 고려함에 따른 조류력 계수는 45%가량 증가하였으며, 모형시험 시 계측된 결과와의 오차가 5%이하로 줄어듦을 확인할 수 있다.
축척비 효과를 배제하고 실제 FSRU와 LNGC에 작용하는 조류력 특성을 살펴보기 위해 실선 크기로 수치계산을 수행하였다. 이 때 조류 속도는 1.029m/s(2knots)를 고려하였으며, 입사각은 0° ~ 180°까지 30° 간격으로 수치계산 하였다. 유체장의 크기는 축척모형 수치계산과 동일한 비율로 설정하였으며, 수치계산에 사용된 격자수는 250~500만개이다. 수치계산으로 얻어진 실선 크기의 FSRU 조류력 계수와 모형 크기의 조류력 계수를 Fig. 5에 도시하여 축척비에 의한 효과가 미미함을 확인하였다. 실선 크기의 수치계산을 수행하여 LNGC의 조류력 계수를 Fig. 6에 도시하였다. LNGC의 경우 수면하부는 유선형 형상을 가지고 있기 때문에, FSRU에 비해 상대적으로 작은 조류력 이 작용함을 알 수 있다.
3.2 직렬배치(1): 조류력
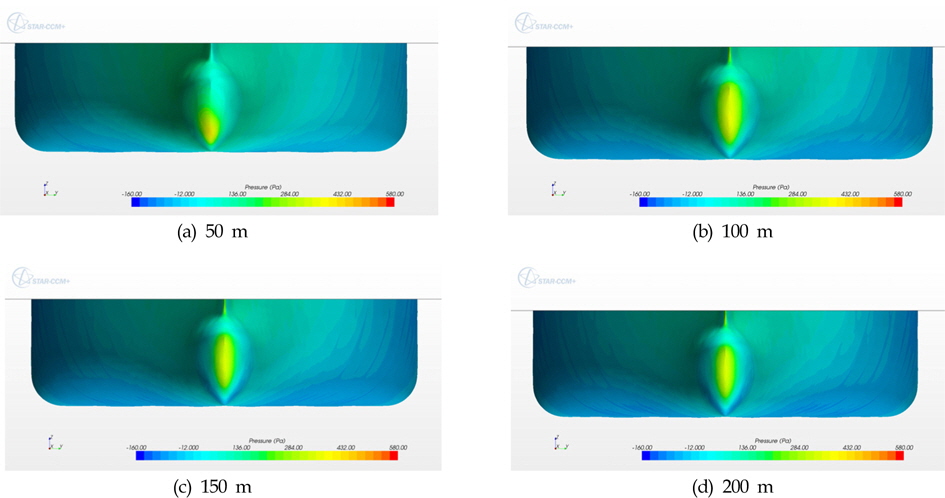
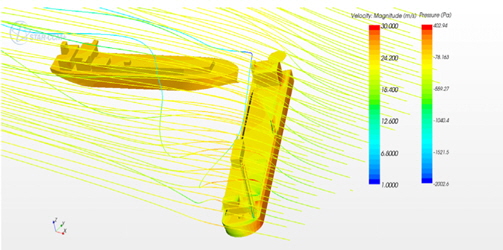
FSRU와 LNGC가 직렬배치 된 상황에서의 조류력 특성을 수치계산을 통해 살펴보았다. 해상 운용시 FSRU는 터렛 계류된 상황으로 선수각은 조류의 방향에 지배적으로 결정이 되므로 입사각은 180°로 고정하였으며, FSRU와 LNGC의 X방향 이격 거리를 50m, 100m, 150m, 200m, 250m로 변화하며 수치계산을 수행하였다. Fig. 7은 선수각 180°, X방향 거리 50m 조건에서, 두 부유체에 작용하는 등압곡선과 유선을 나타낸다. Fig. 8은 X방향의 거리에 따른 조류력 변화를 도시하였다. 두 부유체 사이의 이격 거리가 증가 할수록 LNGC에 작용하는 조류력은 작아지는 반면, FSRU에 작용하는 조류력은 커지는 경향을 보여준다. 특히 두 부유체 사이의 거리가 50m일 때 LNGC에 작용하는 조류력은 간섭 효과에 의해 60% 정도 증가하였다. 이격 거리가 약 150m이상이 되면 두 부유체의 간섭효과는 거의 사라지고, 각각의 조류력 계수는 단독 선체의 값으로 점차 수렴해감을 알 수 있다. Fig. 9은 이격거리에 따라 LNGC에 작용하는 등압곡선을 보여주고 있다. 이격 거리가 멀어질수록 LNGC 전면에서 받는 압력의 크기가 커짐을 확인할 수 있으며, 이는 FSRU 선미 쪽에서 발생하는 후류장에 의해 LNGC 전면의 압력 증가가 발생했음을 알 수 있다.
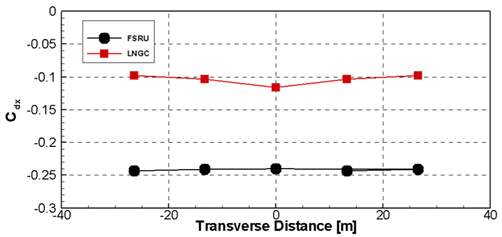
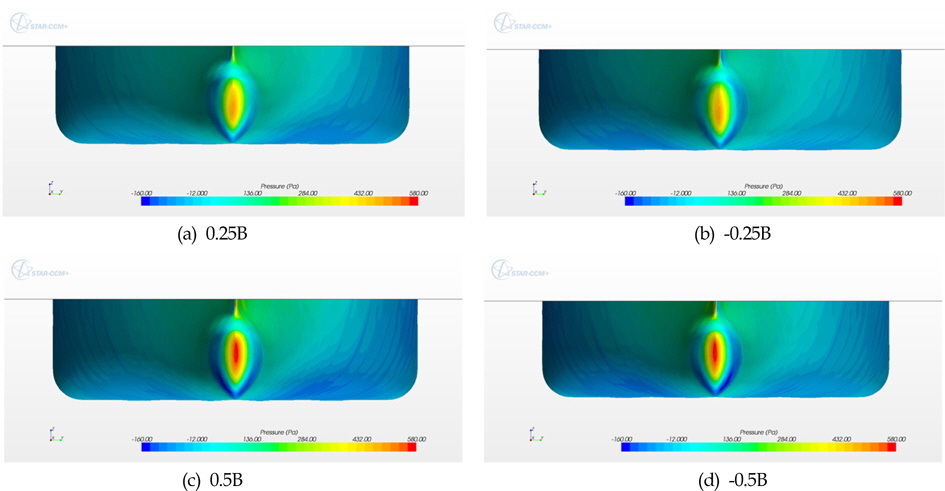
다음으로 두 부유체의 X방향 떨어진 거리는 100m로 유지하며, LNGC를 Y방향으로 FSRU 폭의 0.25B, 0.5B를 이동하여 수치계산 하였다. 이 때 이격거리는 직렬배치 시 통상적인 hawser에 의한 적하역거리를 고려하여 선정하였다. Fig. 10은 LNGC가 0.5B에 위치하였을 때 선체에 작용하는 등압곡선과 유선을 나타내며, Fig. 11,12은 Y방향 이격거리에 따른 조류력 변화 특성을 보여주고 있다. X방향 조류력의 경우는 LNGC가 FSRU 바로 뒤에 위치한 경우에만 약 10%정도의 조류력 변화가 발생하였으며, 측면으로 떨어져서 위치한 경우에는 FSRU의 후류에 의한 영향이 미미하였다. 또한, Y방향 조류력의 경우에는 폭방향 위치의 변화에 따라 작은 변화이지만 조류력 특성의 변화가 있는 것을 확인 할 수 있다. Fig. 13은 측면이동에 따른 LNGC 전면의 등압선도를 보여준다. 선수 정중앙부분의 압력을 제외하고는 전반적으로 유사한 압력분포를 보임을 확인할 수 있다.
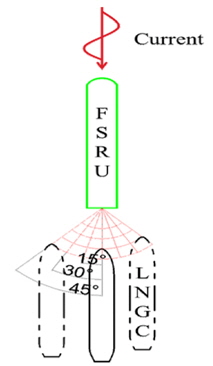
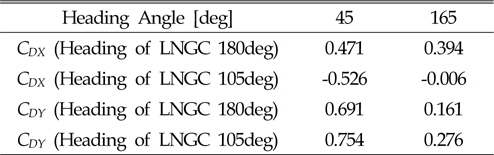
직렬배치 상황에서의 보다 정확한 조류력 변화특성을 살펴보기 위하여, Fig. 14에서처럼 FSRU의 선수각을 180deg로 고정하고, Hawser의 거리를 50m, 75m, 100m, 125m로 변화시켜가면서, LNGC의 각도는 45deg ~ -45deg 각도 범위에 위치한 LNG를 고려하여 수치계산을 수행 하였다. 이 때의 각도와 거리는 LNGC의 DP 시뮬레이션 상의 Watch circle을 고려하여 선정하였다. Fig. 15은 계산 조건 별 조류력 계수의 값을 Contour plot으로 나타내었다. LNGC와 FSRU의 거리가 가까워질수록 FSRU 후류에 영향으로 인하여 LNGC의 조류력 계수가 다소 증가함을 확인할 수 있다. 반면 FSRU는 LNG가 후면에 가까이 다가왔을 때 X-방향 조류력이 다소 감소하는 경향을 보여주었다. 현재 고려한 계산 조건내에서는 Tandem 작업조건시 FSRU는 최대 30%의 조류력 감소가 발생하였으며, LNGC는 최대 45%가량 조류력이 증가하였다.
3.3 직렬배치(2): 풍력
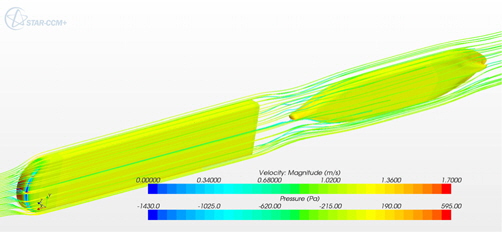
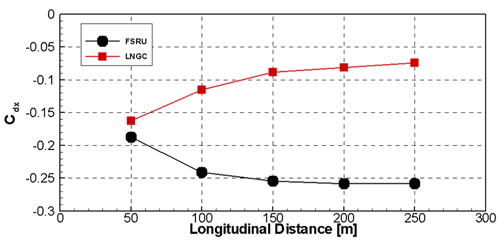
이격거리 100m의 직렬배치 상황에서 20m/s의 풍속장 속의 FSRU와 LNGC의 상부구조물 주위의 유동장을 수치해석하고, 풍력특성을 살펴보았다. 이 때 Reynolds number는 FSRU 4.03 × 108, LNGC 3.41 × 108이며, 바람의 입사각은 180°이다. Table. 3에는 단독 선체에 작용하는 풍하중과 직렬배치 상황에서 FSRU와 LNGC에 작용하는 풍하중을 비교하여 보여주고 있다. 직렬배치일 때 FSRU에 작용하는 풍하중은 큰 변화가 없으나, LNGC에 작용하는 X방향의 풍하중은 단독 선체일 때 보다 약 35%정도 감소한 것을 볼 수 있다. 이는 FSRU의 후류영역에 LNGC가 놓이면서 소위 그림자 효과에 의해 상대적으로 풍압을 적게 받았기 때문이다.
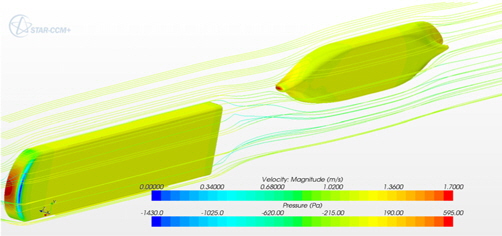
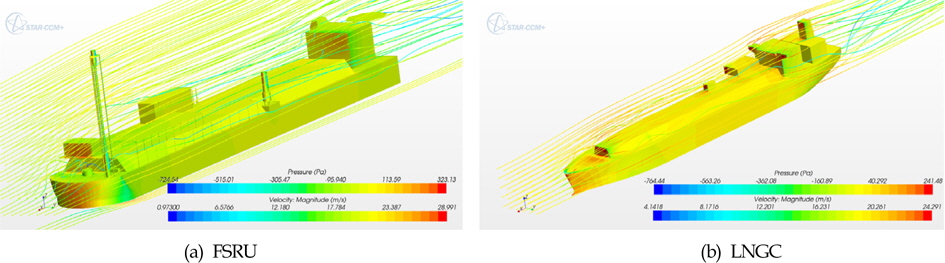
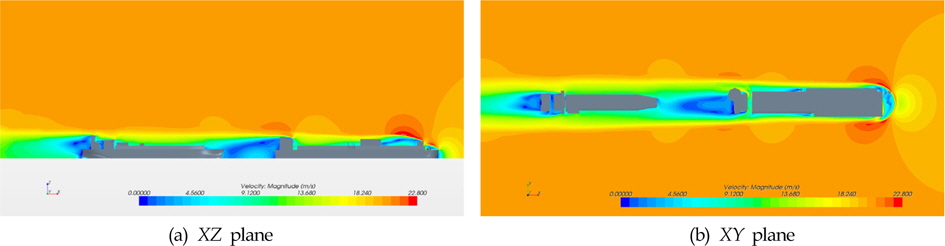
Fig.16에서는 단독 선체의 FSRU와 LNGC에 작용하는 등압곡선과 유선을 보여주고 있다. Fig.17은 직렬배치일 때 두 부유체에 작용하는 등압곡선과 유선을 도시하였으며, Fig.18은 YZ평면과 XY평면에서의 속도 분포를 보여준다. FSRU의 후류장에 LNGC가 위치함에 따라 유동장 및 압력 특성이 단독일 때와는 달라짐을 확인할 수 있다. Fig. 19는 단독 선체와 직렬배치 일때 LNGC에 작용하는 등압곡선을 나타내고 있다. 그림을 살펴보면 LNGC에 작용하는 풍압은 단독조건일 때 보다 직렬배치조건에서 현저히 감소하는 것을 알 수 있다.
다음으로 Hawser의 길이를 100m로 정하고 직렬배치된 상황에서의 FSRU와 LNGC 각각의 풍하중계수를 수치계산하고 LNGC가 FSRU의 후류장에 가장 큰 영향을 받는 각도를 결정하여 두 부유체에 작용하는 풍하중계수를 수치계산하였다. Fig. 20에서는 그림으로 수치계산에 사용된 직렬배치 구성을 나타내었다. 직렬배치로 고려된 두가지 상황에서 FSRU와 LNGC 두 부유체에 작용하는 풍하중 계수를 Table 4에 비교하였다. LNGC가 FSRU 후미에 직선상으로 위치하여 있을 때는 LNGC의 X방향 풍하중은 단독 선체일 때의 결과보다 40%정도가 감소되었으며, Y방향의 풍하중은 변화가 많지 않음을 확인할 수 있다. FSRU와 LNGC의 선수각을 변화시켜 FSRU의 후류장에 LNGC가 위치해있을 때 X방향의 풍하중은 최대 80% 감소하는 것을 확인할 수 있으며, Y방향의 풍하중은 증가하는 것을 확인할 수있다.
4. 결 론
본 논문에서는 직렬배치 상황에서 FSRU과 LNGC에 작용하는 조류력 및 풍력 특성을 CFD를 이용한 수치계산을 통하여 고찰하였다. 먼저 FSRU단독 조건의 조류력에 대해 모형시험 결과와 비교함으로 수치 모델 및 격자에 대한 검증을 수행하였다. 동 수치기법을 활용하여 FSRU와 LNGC의 직렬 배치 조건에서 조류력 및 풍력 특성에 대한 수치 계산을 수행하였다. 이 때 조류력의 경우 FSRU와 LNGC의 이격거리를 달리하며 그 영향을 검토하였다. 조류력의 경우 FSRU의 후류장에 의해 LNGC의 조류력이 최대 45%가량 증가하였으며, 반면 FSRU는 LNG가 후면에 가까이 위치했을 때 30% 가량의 조류력 감소가 발생하였다. 이러한 간섭 효과는 전후 방향 이격거리에 따라 크게 변화할수 있음을 CFD 계산을 통해 제시 하였다. 풍하중의 경우 FSRU의 후류영역에 LNGC가 위치함에 따라 그림자 효과로 인하여 35% ~ 80%가량 항력이 감소할 수 있음을 수치계산으로부터 확인할 수 있었다. 또한 FSRU의 입사되는 유동의 방향에 따라 후미의 후류장의 크기가 바뀌고, 두 부유체의 상대적인 위치가 후류에 의한 유체력 간섭 효과가 크게 바뀜을 확인 할 수 있었다. 추후 모형 시험과의 비교를 통해 검증작업을 진행할 필요성이 있으며, FSRU와 LNGC의 다양한 위치관계를 고려하여 그림자 효과에 대한 정량적 특성을 체계적으로 제시할 필요성이 있다.
Notes
It is noted that this paper is revised edition based on proceedings of KAOST 2013 in Jeju.
Acknowledgements
본 연구는 해양수산부(한국해양과학기술진흥원)의 지원으로 수행한 "심해공학수조 운용을 위한 연구 인프라 구축 및 심해플랜트 Pre-Feed 원천 핵심기술 개발" 과제와 지식경제부(산업기술평가관리원)의 지원으로 수행한 "LNG FSRU 구조물-계류 시스템 설계핵심 기술 개발" 과제의 지원으로 수행된 연구결과 중 일부임을 밝히며, 연구비 지원에 감사드립니다.
References
Koop, A., Klaij, C., Vaz, G., 2010. Predicting Wind Loads for FPSO Tandem Offloading Using CFD. Proceeding of ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers, OMAE2010-20284, 533-546.
Koop A., Klaij C., Vaz G.. Predicting Wind Loads for FPSO Tandem Offloading Using CFD, OMAE2010-20284 In : Proceeding of ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers; 2010. p. 533–546.Jun, J.H., Lee, S.E., Kwon, J.W., Son, J.W., 2012. Analysis of Flow around Ship Using Unstructured Grid. 2012 Korean Society for Computational Fluids Engineering, Annual Conference, 187-193.
Jun J.H., Lee S.E., Kwon J.W., Son J.W.. Analysis of Flow around Ship Using Unstructured Grid In : 2012 Korean Society for Computational Fluids Engineering, Annual Conference; 2012. p. 187–193.Koo, M.J., Ha, M.K., Choi, J.W., Bae, J.H., 2004. The Study on Wind Shielding Effects According to Distance between Two Ships. 2004 Mechanical Science and Technology, Annual Conference, 1413-1417.
Koo M.J., Ha M.K., Choi J.W., Bae J.H.. The Study on Wind Shielding Effects According to Distance Between Two Ships In : 2004 Mechanical Science and Technology, Annual Conference; 2004. p. 1413–1417.Park, Y.S., Kim, W.J., Jun, B.H., 2012. Flow Analysis around Multi-Legged Underwater Robot "Crabster" to Evaluate Current Loads. Journal of Ocean Engineering and Technology, 26(5), 47-55.
Park Y.S., Kim W.J., Jun B.H.. Flow Analysis around Multi-Legged Underwater Robot "Crabster" to Evaluate Current Loads. Journal of Ocean Engineering and Technology 2012;26(5):47–54. 10.5574/KSOE.2012.26.5.047.Souzam J.R., Ragazzo, C.G., 2006. Hydrodynamic Interaction of Two Ships in Tandem under Current. Proceedings of the Sixteenth (2006) International Offshore and Polar Engineering Conference, 150-157.
Souzam J.R., Ragazzo C.G.. Hydrodynamic Interaction of Two Ships in Tandem under Current In : Proceedings of the Sixteenth (2006) International Offshore and Polar Engineering Conference; 2006. p. 150–157.Tabaczek, T., Kulczyk, J., Zawislak, M, 2007. Analysis of Hull Resistance of Pushed Barges in Shallow Water. Pocish Maritime Research 1(51), 14, 10-15.
Tabaczek T., Kulczyk J., Zawislak M. Analysis of Hull Resistance of Pushed Barges in Shallow Water. Pocish Maritime Research 2007;14:10–15.Tannuri, E.A, Fucatu, C.H, Rossin, B.D, Motagnini, R.C., Ferrira, M.D., 2010. Wind Shielding Effects on DP System of a Shuttle Tanker. Proceeding of ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering, American Society of Mechanical Engineers, OMAE2010-20148, 143-149..
Tannuri E.A, Fucatu C.H, Rossin B.D, Motagnini R.C., Ferrira M.D.. Wind Shielding Effects on DP System of a Shuttle Tanker, OMAE2010-20148 In : Proceeding of ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers; 2010. p. 143–149.Yuck, R.H., Choi, H,S., Hong, S.Y., 2006. Estimation of Current Loads on Offshore Using CFD. Journal of Ship & Ocean Technology, 10(1), 27-37.
Yuck R.H., Choi, H S., Hong S.Y.. Estimation of Current Loads on Offshore Vessels Using CFD. Journal of Ship & Ocean Technology 2006;10(1):27–37.Yuck, R.H., Park, M.K., Choi, H.S., 2007. Estimation of Current Loads on Side-by-Side Moored Two Vessels. Proceeding of the Seventeenth (2007) International Offshore and Polar Engineering Conference, 338-342.
Yuck R.H., Park M.K., Choi H.S.. Estimation of Current Loads on Side-by-Side Moored Two Vessels In : Proceeding of the Seventeenth (2007) International Offshore and Polar Engineering Conference; 2007. p. 338–342.