1. ÏÑú ΰÝ
ÏßÄÏÜçÏÝÅÏù∏ Í≥ÝÏúÝÍ∞Ä ÌòÑÏÉÅÍ≥º ÏÑ∏Í≥ÑÏÝÅÏúºÎ°ú Í∏âÍ≤©ÌïòÍ≤å ϶ùÍ∞ÄÌïòÎäî ÏóêÎÑàÏßÄ ÏàòÏöîΰú Ïù∏Ìï¥ Ïú°ÏÉÅÏóêÏÑú Í∞úÎ∞ú Í∞ÄÎä•Ìïú ÏúÝÏÝÑÏúºÎ°úÎäî Ïù¥Î•º Ï∂©Ï°±ÏãúÌǧÏßÄ Î™ªÌïòÎØÄΰú Ìï¥ÏñëÏúÝÏÝÑÏùò ÏùòÏ°¥ÎèÑÍ∞Ä Í∞àÏàòΰù ÎÜíÏïÑÏßÄÍ≥Ý ÏûàÎ㧠(SERI, 2012). ÏÑùÏúÝΕº ÏÉùÏÇ∞ÌïòÎäî Ìï¥ÏñëÌîåÎûúÌä∏ ϧë FPSO(Floating, production, storage and offloading)Îäî ÏÑÝÏ≤¥Î∂ÄÎ∂ÑÏùÑ ÏõêÏúÝÏÝÄÏû• ÌɱÌŨΰú ÏǨÏö©ÌïòÍ≥Ý Í∞ëÌåêÏóê ÏõêÏúÝ ÏÝïÏÝú ÏãúÏä§ÌÖúÏùÑ ÌÉëÏû¨ÌïòÏó¨ ÏÉùÏÇ∞ÏѧÎπÑΰú ÏǨÏö©ÌïúÎã§. Ïù¥Îäî Í∏∞Ï°¥Ïùò Í≥ÝÏÝïÌòï Ìï¥ÏñëÌîåÎûúÌä∏Ïóê ÎπÑÌï¥ Ïã¨Ìï¥ ÏúÝÏÝÑÏùÑ Í∞úÎ∞úÌïòÎäîÎç∞ ÏúÝζ¨ÌïòΩ∞, Ìïú ÏúÝÏÝÑÏóêÏÑú ÏÉùÏÇ∞ÏùÑ ÎÅùÎÇ∏ ÌõÑ Îã§Î•∏ ÏúÝÏÝÑÏúºÎ°ú Ïù¥ÎèôÌïÝ Ïàò ÏûàÎã§Îäî Ïù¥ÏÝêÏù¥ ÏûàÎã§. FPSOÏùò ͵¨Ï°∞Îäî ÌŨÍ≤å Ïã¨Ìï¥ÏÝÄÏãúÏä§ÌÖú(Subsea system), ÏÑÝÏ≤¥(Hull), ÌÑ∞ÎÝõ(Turret), ÏÉÅÎ∂Ä͵¨Ï°∞Ψº(Topside)ΰú ÎÇòÎàÑÏñ¥Ïßà Ïàò ÏûàÏúºÎ©∞, ÏÉÅÎ∂Ä͵¨Ï°∞ΨºÏùÄ ÏúÝÌã∏ζ¨Ìã∞ ÏãúÏä§ÌÖú(Utility system)Í≥º Í≥µÏÝï ÏãúÏä§ÌÖú(Processing system)ÏúºÎ°ú ÎÇòÎàÑÏñ¥ÏßÑÎã§. ÏÉÅÎ∂Ä͵¨Ï°∞ΨºÏùÄ ÏÝúÌïúÎêú Ω¥ÏÝÅÏóê ÎßéÏùÄ ÏàòÏùò Ïû•ÎπÑÍ∞Ä Î∞∞ÏπòÎêòÏñ¥Ïïº ÌïòÎØÄΰú, Í≥µÍ∞ÑÏùÑ Ìö®Ïú®ÏÝÅÏúºÎ°ú ÌôúÏö©ÌïòÍ∏∞ ÏúÑÌïòÏó¨ Ïú°ÏÉÅÌîåÎûúÌä∏ÏôÄÎäî Îã¨Î¶¨ 3Ï∞®ÏõêÏÝÅÏù∏ Îã§Ï∏µ Í∞ëÌåê(Multi-deck)ÏóêÏÑúÏùò Ïû•ÎπÑÎ∞∞ÏπòÍ∞Ä Ïù¥Î£®Ïñ¥ÏßÑÎã§. ÌäπÌûà, ÏÉÅÎ∂Ä͵¨Ï°∞Ψº ϧëÏóêÏÑú Í≥µÏÝï ÏãúÏä§ÌÖúÏùÄ ÌôîÏû¨ÏôÄ Ìè≠Î∞úÏùò ÏúÑÌóòÏѱÏù¥ ÌÅ∞ Í≥µÏÝï Ïû•ÎπÑÎì§Ïù¥ Î∞ÄÏßëÎêòÏñ¥ ÏûàÍ∏∞ ÎïåΨ∏Ïóê Í≥µÍ∞ÑÏÝÅÏù∏ ÏÝúÏïΩÏ°∞ͱ¥ ÎÇ¥ÏóêÏÑú Í≤ΩÏÝúÏѱÍ≥º ÏúÑÌóòÎèÑ Îì±Ïùò Î≥µÌï©ÏÝÅÏù∏ ÏöîÏÜåÎì§Ïù¥ Í≥ÝÎݧÎêòÏñ¥Ïïº ÌïúÎã§.
Í¥ÄÎÝ® Ïó∞͵¨ ÌòÑÌô©ÏúºÎ°ú Patsiatzis and Papageorgiou(2002)Îäî Ïó¨Îü¨ Ï¢ÖΕòÏùò Ïú°ÏÉÅ ÌôîÌïô Í≥µÏÝï ÌîåÎûúÌä∏Ïóê ÎåÄÌïòÏó¨ Îã§Ï∏µ ϵúÏÝÅÎ∞∞ÏπòΕº ÏàòÌñâÌïòÏòÄÎã§. Ïó∞Í≤∞ÎêòÎäî Ïû•ÎπÑÏǨÏù¥Ïùò ÌååÏù¥ÌîÑ, ÌéåÌîÑÏùò ÏѧÏπòÎπÑÏö©Í≥º Ï∏µÏùò Í∞úÏàò, Ω¥ÏÝÅÏóê Îî∞Ε∏ ͱ¥ÏѧÎπÑÏö©Ïùò Ìï©ÏùÑ Î™©ÏÝÅÌï®Ïàòΰú ÏÝïÏùòÌïòÏòÄÍ≥Ý, Í∞ëÌåê ÌŨÍ∏∞Ïóê Îî∞Ε∏ ÏÝúÌïúÏ°∞ͱ¥Í≥º Ι©ÏÝÅÌï®ÏàòΕº ÌòºÌï©ÏÝïÏàòÏÑÝÌòïÍ≥ÑÌöçÎ≤ï(Mixed integer linear programming)Ïùò ÌòïÌÉúΰú ÌíÄÏù¥ÌïòÏó¨ ϵúÏÝÅÏùò Î∞∞ÏπòΕº Í≤∞ÏÝïÌïòÏòÄÎã§.
Park et al.(2011)ÏùÄ ÏïàÏÝÑÏѱÏùÑ Í≥ÝÎݧÌïú Îã§Ï∏µ ÌôîÌïôÍ≥µÏÝïÌîåÎûúÌä∏Ïùò Ïû•ÎπÑ ÏµúÏÝÅÎ∞∞ÏπòΕº ÏàòÌñâÌïòÏòÄÎã§. ÏѧÍ≥ÑÎ≥ÄÏàò Î∞è ÏÝúÌïúÏ°∞ͱ¥Í≥º Ïù¥Îì§Ïùò ÏàòÌïôÏÝŠΙ®Îç∏ÎßÅÏùÄ Patsiatzis and Papageorgiou(2002)ÏôÄ Í∞ôÏù¥ ÏÝÅÏö©ÌïòÏòÄÍ≥Ý, TNT Îì±Í∞ÄÎ∞©Î≤ï(Trinitrotoluene equivalency method)ÏúºÎ°ú ÏòàÏ∏°Ìïú Ïû•ÎπÑ ÏÜêÏÉÅÏóê Í¥ÄÎÝ®Îêú ÎπÑÏö©(Penteado and Ciric, 1996)ÏùÑ Î™©ÏÝÅÌï®ÏàòÏóê Ï∂îÍ∞ÄÌïòÏòÄÎã§.
Yu(2010)Îäî Ìï¥ÏñëÌîåÎûúÌä∏ ÌôîÏû¨ Î∞è Í∞ÄÏä§ ÌôïÏÇ∞ Í∑∏ζ¨Í≥Ý Ìè≠Î∞úÌòÑÏÉÅÏóê Í¥ÄÎÝ®ÎêòÎäî Î≥ÄÏàòÎì§ÏùÑ ÏÝïÏùòÌïòÍ≥Ý, Í∑∏ Î≥ÄÏàòÏóê ÎåÄÌïú Ïù¥ÏÝÑ ÏǨÍ≥Ý Îç∞Ïù¥ÌÑ∞Εº ÌôïΕÝÏÝÅÏúºÎ°ú ÏÝëÍ∑ºÌïòÏó¨ ÏãÝ΢∞ÌïÝ Ïàò ÏûàÎäî ÏǨÍ≥Ý ÏãúÎÇòζ¨Ïò§Î•º ÏÑÝÏÝïÌïòÎäî ÏÝàÏ∞®Î•º ÏÝúÏãúÌïòÏòÄÎã§.
Kim(2013)ÏùÄ FPSOÏùò Î∂Ñζ¨ Ι®Îìà(Separation module) ÎÇ¥Î∂ÄÏùò Ïû•ÎπÑΕº ÎåÄÏÉÅÏúºÎ°ú ÌïòÏó¨, ÌååÏù¥ÌîÑ ÏѧÏπòÎπÑÏö©Í≥º ÌôîÏû¨ Î∞è Ìè≠Î∞ú ÌîºÌï¥ÎπÑÏö©ÏùÑ ÎçîÌïú Í∞íÏùÑ ÏµúÏÜåÌôî ÏãúÌǧÎäî Îã§Ï∏µ ϵúÏÝÅÎ∞∞ÏπòΕº ÏãúÎèÑÌïòÏòÄÎã§. ÎòêÌïú ÏõêÌܵÌòï(Cylindrical) FPSOΕº ÎåÄÏÉÅÏúºÎ°ú Í≥µÏÝï Ι®ÎìàÏùò ÌèâΩ¥ ϵúÏÝÅÎ∞∞ÏπòΕº ÏàòÌñâÌïòÏòÄÏúºÎ©∞, Ι©ÏÝÅÌï®ÏàòΰúÎäî ÌååÏù¥ÌîÑ ÏѧÏπò, ÌôîÏû¨ Î∞è Ìè≠Î∞ú ÌîºÌï¥, Í¥Äζ¨ÎèÑΕº ÎπÑÏö©ÏúºÎ°ú ÌܵÌï©ÌïòÏó¨ ÏѧÏÝïÌïòÏòÄÎã§. ϵúÏ¢ÖÏÝÅÏúºÎ°ú, ÏÝúÌïúÏ°∞ͱ¥Í≥º Ι©ÏÝÅÌï®ÏàòΕº ÌòºÌï©ÏÝïÏàòÏÑÝÌòïÍ≥ÑÌöçÎ≤ï ÌòïÌÉúÏùò ÏàòÌïôÏÝŠΙ®Îç∏ÎßÅÏùÑ ÌܵÌï¥ ÌíÄÏù¥ÌïòÏó¨ ϵúÏÝÅÏùò Î∞∞ÏπòΕº Í≤∞ÏÝïÌïòÏòÄÎã§.
Î≥∏ Ïó∞͵¨ÏóêÏÑúÎäî Î∂ÅÌï¥ÏßÄÏó≠Ïùò ÎÖ∏Ε¥Ïõ®Ïù¥ Jordb√¶r FieldÏóêÏÑú ÌïòΣ®Ïóê 63,000BPD ÏÝïÎèÑÏùò ÏÑùÏúÝΕº ÏÉùÏÇ∞ÌïÝ Ïàò ÏûàÎäî FPSOÏóê ÎåÄÌïòÏó¨ Í∑∏ ÏÉÅÎ∂Ä͵¨Ï°∞Ψº ϧë Í∞ÄÏû• ÎßéÏùÄ Í≥µÏÝï Ïû•ÎπÑΕº Í∞ÄÏßÄÎäî Í≥ÝÏïïÍ∞ÄÏä§ ÏïïÏ∂ïΙ®Îìà(HP gas compression module) ÎÇ¥Î∂ÄÏùò Ïû•ÎπÑÎì§ÏùÑ ÎåÄÏÉÅÏúºÎ°ú ÌïòÏó¨, Í≥µÍ∞ÑÏÝÅÏù∏ ÏÝúÏïΩÏ°∞ͱ¥Í≥º Í≤ΩÏÝúÏѱ Î∞è ÏúÑÌóòÎèÑΕº Í≥ÝÎݧÌïú Îã§Ï∏µ ϵúÏÝÅÎ∞∞ÏπòΕº ÏàòÌñâÌïòÏòÄÎã§. Ïû•ÎπÑÍ∞ÑÏùò ϵúÏÜåͱ∞ζ¨Î•º Í∑úÏÝïÌïòÏó¨ ÏúÝÏßÄÎ≥¥Ïàò Ï∏°Î©¥ÏùÑ Í≥ÝÎݧÌïòÏòÄÍ≥Ý, Ψ¥Í≤å ÏïàÏÝïÏѱÏùÑ ÏúÑÌï¥ Î™®Îìà ÎÇ¥Î∂ÄÏùò ÏÝÑÏ≤¥Ïû•ÎπÑÏóê ÎåÄÌïú Ψ¥Í≤åϧëÏã¨Ïù¥ Í∞ëÌåê ϧëÏïô ÎÇ¥Î∂ÄÏóê ÏúÑÏπòÌïòÎèÑΰù ÏÝúÌïúÏ°∞ͱ¥ÏùÑ ÏѧÏÝïÌïòÏòÄÎã§. Ι©ÏÝÅÌï®ÏàòΰúÎäî Patsiazis and Papageorgiou(2002)Ïùò ÌååÏù¥ÌîÑ, ÌéåÌîÑ ÏѧÏπòÎπÑÏö©ÏóêÏÑú ÏúÝÎèô Î∞©Ìñ•Ïóê Îî∞Ε∏ Ï∞®Ïù¥Î•º Ï∂îÍ∞ÄÌïòÏó¨ Í≤ΩÏÝúÏѱÏùÑ ÌèâÍ∞ÄÌïòÏòÄÎã§. ÎòêÌïú, Ïù¥ÏÝÑ ÏǨÍ≥Ý Îç∞Ïù¥ÌÑ∞Εº Î∞îÌÉïÏúºÎ°ú Í∞ÄÎä•Ìïú ÌôîÏû¨ÏǨÍ≥ÝÏùò ÏãúÎÇòζ¨Ïò§Î•º ÏÑÝÏÝïÌïú Îí§ ÌôîÏû¨Í∞Ä Î∞õÎäî Î∞îÎûåÏùò ÏòÅÌñ•ÏùÑ ÌçºÏßÄ ÏßëÌï©ÏúºÎ°ú ÏѧÏÝïÌïòÏòÄÎã§. ÌôîÏû¨ÎÇò Ìè≠Î∞úÏùÑ Ïó¨Îü¨ Í∞ÄÏßÄ Í≤ΩÌóòÏãùÏúºÎ°ú Í≥ÑÏÇ∞ÌïòÏó¨ ÏúÑÌóòÎèÑΕº ÏÝïÎüâÌôîÌïòÎäîÎç∞ ÏǨÏö©ÎêòÎäî S/WÏù∏ Phast7.0 (DNV GL, 2014)ÏùÑ ÏǨÏö©ÌïòÏó¨, ÌôîÏû¨ Î∞úÏÉù Ïãú Ïù∏ÏÝëÏû•ÎπÑÍ∞Ä Î∞õÎäî Î≥µÏǨÏó¥ÎüâÏùÑ Î∞îÌÉïÏúºÎ°ú ÏúÑÌóòÎèÑΕº ÌèâÍ∞ÄÌïòÏòÄÎã§. Ïù¥Îü¨Ìïú Îëê Í∞ÄÏßÄ Î™©ÏÝÅÌï®ÏàòÏóê ÎåÄÌï¥, ÏúÝÏÝÑÏûê ÏïåÍ≥Ýζ¨Ï¶òÏùÑ Ïù¥Ïö©ÌïòÏó¨ ÌååÎÝàÌÜÝ ÏµúÏÝÅ (Pareto optimality)ÏùÑ ÌÉêÏÉâÌï®ÏúºÎ°úÏç® Îã§Î™©ÏÝŠϵúÏÝÅÌôîÏóêÏÑú Ι©ÏÝÅÌï®ÏàòÏùò ϧëÏöîÎèÑÏóê Îî∞Îùº ÏѧÍ≥ÑÏûêÍ∞Ä ÏúµÌܵÏѱ ÏûàÍ≤å ϵúÏÝÅÌï¥Î•º ÏÑÝÌÉùÌïÝ Ïàò ÏûàÎèÑΰù ÌïòÏòÄÎã§.
2. FPSO ÏÉÅÎ∂Ä͵¨Ï°∞ΨºÏùò Í≥µÏÝï ÌùêζÑÍ≥º Í≥µÏÝï Ïû•ÎπÑ
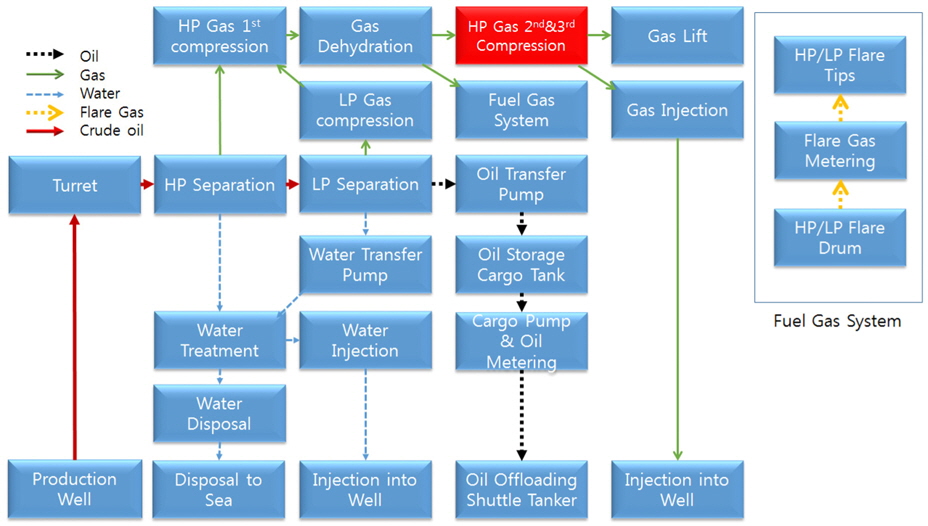
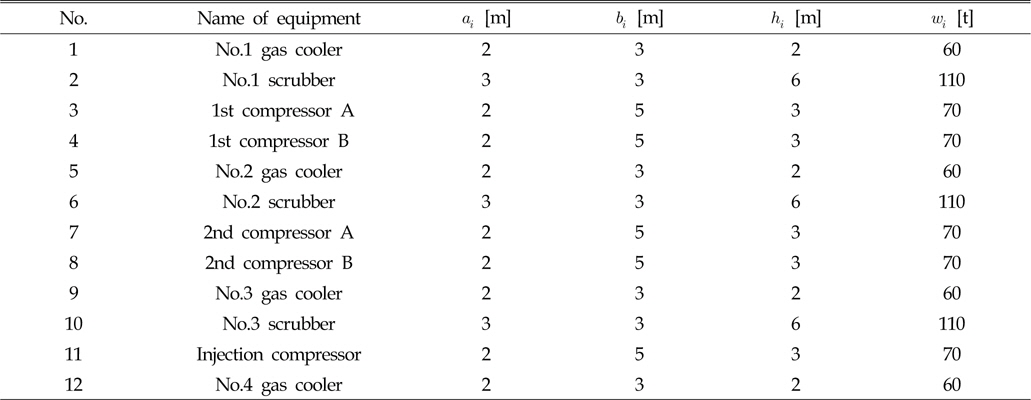
FPSOÏùò ÏõêÏúÝ ÏÝïÏÝú Í≥ºÏÝïÏùÄ Fig. 1Ïùò Í≥µÏÝï ÌùêζÑÎèÑÏôÄ Í∞ôÏù¥ ÏúÝÏÝïÏóêÏÑú Ïò¨ÎùºÏò® ÏõêÏúÝÍ∞Ä ÌÑ∞ÎÝõÏùÑ Í±∞Ï≥ê Í≥ÝÏïï/ÏÝÄÏïï Î∂Ñζ¨(HP/LP separation)ÏûëÏóÖÏùÑ ÌܵÌï¥ Î¨º, Í∏∞ζÑ, Í∞ÄÏä§Î°ú Î∂Ñζ¨ÎêòÏñ¥ Í∞ÅÍ∞ÅÏùÑ Ï≤òζ¨ÌïòÎäî ÏãúÏä§ÌÖúÏúºÎ°ú Î≥¥ÎÇ¥ÏßÑÎã§. Ïù¥ÏôÄ Í∞ôÏùÄ ÏûëÏóÖÏùÄ ÎßéÏùÄ ÏàòÏùò Í≥µÏÝï Ïû•ÎπÑΕº ÌïÑÏöîΰú ÌïòΩ∞, Í∞ôÏùÄ Í∏∞Îä•ÏùÑ ÌïòÎäî Ïû•ÎπÑÎì§Îźζ¨ Ι®ÏïÑÏÑú Ι®ÎìàÏùò Îã®ÏúÑΰú Î∞∞ÏπòÌïòÎäî Í≤ÉÏù¥ Ìö®Ïú®ÏÝÅÏù¥Îã§. ÏùºÎ∞òÏÝÅÏúºÎ°ú Í≥µÏÝï ÏãúÏä§ÌÖúÏùÑ Íµ¨ÏѱÌïòÎäî ÌïòÏúÑ ÏãúÏä§ÌÖúÏùÄ Î∂Ñζ¨ ÏãúÏä§ÌÖú(Separation system), Ïò§ÏùºÏ≤òζ¨ ÏãúÏä§ÌÖú(Oil processing system), Í∞ÄÏä§Ï≤òζ¨ ÏãúÏä§ÌÖú(Gas processing system), ÏàòÏ≤òζ¨ ÏãúÏä§ÌÖú(Water processing system), ÌîåÎûòÏñ¥ ÏãúÏä§ÌÖú(Flare system)Ïù¥ ÏûàÏúºÎ©∞, Í∞ÄÏä§Ï≤òζ¨ ÏãúÏä§ÌÖúÏùÄ Íµ¨Ï≤¥ÏÝÅÏù∏ Í∏∞Îä•Ïóê Îî∞Îùº ÌÉàÏàò Ι®Îìà(Dehydration module), Í≥ÝÏïïÍ∞ÄÏä§ ÏïïÏ∂ïΙ®Îìà, ÏÝÄÏïïÍ∞ÄÏä§ ÏïïÏ∂ïΙ®Îìà(LP gas compression module)ΰú ͵¨ÏѱÎêúÎã§. Î≥∏ Ïó∞͵¨Ïùò ÎåÄÏÉÅÏù∏ Í≥ÝÏïïÍ∞ÄÏä§ ÏïïÏ∂ïΙ®ÎìàÏùÄ ÏùºÎ∞òÏÝÅÏúºÎ°ú Í∞ÄÏû• ÎßéÏùÄ ÏàòÏùò ÎÇ¥Î∂Ä Ïû•ÎπÑΕº Í∞ÄÏßÄΩ∞, ÌÉàÏàòÍ≥ºÏÝïÏùÑ Í±∞Ïπú Í∞ÄÏä§Í∞Ä ÏúÝÏûÖÎêòΩ¥ Fig. 2Ïùò Í≥µÏÝï ÌùêζÑÎèÑÏôÄ Í∞ôÏùÄ ÏïïÏ∂ïÍ≥ºÏÝïÏùÑ Í±∞Ï≥ê ÏúÝÏÝïÏúºÎ°ú Ï£ºÏûÖÎêÝ Í∞ÄÏä§Î•º ÎßåÎìúÎäî Ïó≠ÌïÝÏùÑ ÌïúÎã§. Ι®Îìà ÎÇ¥Î∂ÄÏùò ͵¨Ï≤¥ÏÝÅÏù∏ Ïû•ÎπÑ Í∞úÏàòÎÇò Ïö©ÎüâÏùÄ FPSOÏôÄ Í∞úÎ∞ú ÏúÝÏÝÑÏùò ÌŨÍ∏∞Ïóê Îî∞Îùº Îã§Î•¥ÎÇò, Î≥∏ Ïó∞͵¨ÏóêÏÑúÎäî Fig. 2ÏôÄ Í∞ôÏù¥ Í≥ÝÏïïÍ∞ÄÏä§ ÏïïÏ∂ïΙ®ÎìàÏù¥ 3Î≤àÏùò ÏïïÏ∂ïÍ≥ºÏÝïÏùÑ ÏàòÌñâÌïòΩ∞, Í∞ÄÏä§ ÎÉâÍ∞ÅÍ∏∞(Gas cooler) 4ÎåÄ, Ïä§ÌŨÎü¨Î≤Ñ(Scrubber) 3ÎåÄ, Í∞ÄÏä§ÏïïÏ∂ïÍ∏∞(Gas compressor) 5ÎåÄΰú ͵¨ÏѱÎêòÏñ¥ Ï¥ù 12Í∞úÏùò Ïû•ÎπÑΕº Í∞ÄÏßÄÎäî Í≤ÉÏúºÎ°ú Í∞ÄÏÝïÌïòÍ≥Ý, Ïù¥Îì§ Ïû•ÎπÑΕº 2Ï∏µ ͵¨Ï°∞Ïùò Í∞ëÌåêÏóê Î∞∞ÏπòÌïòÏòÄÎã§. Ïû•ÎπÑÎì§Ïùò ÌŨÍ∏∞ÏôÄ Î¨¥Í≤åÎäî Table 1Í≥º Í∞ôÏù¥ Í∞ÄÏÝïÌïòÏòÄÎã§.
3. Í≥ÝÏïïÍ∞ÄÏä§ ÏïïÏ∂ïΙ®Îìà Ïû•ÎπÑÏùò Îã§Ï∏µ ϵúÏÝÅÎ∞∞Ïπò Î∞è Î∂ÑÏÑù
3.1 설계 변수
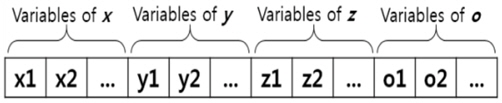
ÏѧÍ≥Ñ Î≥ÄÏàòΰúÎäî Í∞Å Ïû•ÎπÑ Ï§ëÏã¨Ïùò 3Ï∞®ÏõêÏÝÅ ÏúÑÏπòÏ¢åÌëúÏôÄ Ïû•ÎπÑÏùò Î∞∞Ïπò Î∞©Ìñ•ÏúºÎ°ú Î≥ÄÏàòΕº ÏѧÏÝïÌïòÏòÄÏúºÎ©∞ Ïó∞ÏÜçÎ≥ÄÏàò(Continuous variables)Ïù∏ xi,yi (Ïû•ÎπÑ i ϧëÏã¨Ïùò x, yÏ¢åÌëú)ÏôÄ Ïù¥ÏÇ∞Î≥ÄÏàò (Discrete variables)Ïù∏ zi (Ïû•ÎπÑ i ϧëÏã¨Ïùò zÏ¢åÌëú)ΰú ÏѧÏÝïÌïòÏòÄÏúºÎ©∞, Ïû•ÎπÑÎäî Í∞ëÌåêÏúÑÏóê Ï°¥Ïû¨Ìï¥Ïïº ÌïòÎØÄΰú, 'Ïû•ÎπÑ iÏùò Î∞îÎã•ÏóêÏÑú ϧëÏã¨ÍπåÏßÄ ÎÜíÏù¥ + Í∞ëÌåêÎÜíÏù¥ √ó Í∞ëÌåê Ï∏µ(n)'Ïùò Í∞íÎßå Í∞ÄÏßà Ïàò ÏûàÎã§(Ïù¥Ï∏µ Í∞ëÌåêÏù¥ÎØÄΰú n= 0, 1). Îòê ÌïòÎÇòÏùò Ïù¥ÏÇ∞Î≥ÄÏàòÏù∏ oi (Ïû•ÎπÑ iÏùò ÌŨÍ∏∞ ai ÏôÄ bi ϧëai Í∞Ä xÏ∂ïÍ≥º ÌèâÌñâÌïÝ Í≤ΩÏö∞ 1, bi Í∞Ä xÏ∂ïÍ≥º ÌèâÌñâÌïÝ Í≤ΩÏö∞ 0)Îäî ÌèâΩ¥ ÏÉÅ ÏßÅÏǨÍ∞ÅÌòïÏúºÎ°ú Ι®Îç∏ÎßÅÎêòÎäî Ïû•ÎπÑÍ∞Ä Í∞ëÌåê ÏúÑÏóê ÎÜìÏù¥Îäî Î∞©Ìñ•ÏùÑ 2Í∞ÄÏßÄΰú ͵¨Î∂ÑÌïòÎäî Î≥ÄÏàòΰúÏç® Ïû•ÎπÑÏùò Î∞∞Ïπò Î∞©Ìñ•Ïóê Îî∞Îùº ÌååÏù¥ÌîÑÏùò ÏÉùÏÇ∞ÏѱÏóê ÏòÅÌñ•ÏùÑ ÎØ∏ÏπúÎã§. ÏúÝÏÝÑÏûê ÏïåÍ≥Ýζ¨Ï¶òÏùÑ Ïù¥Ïö©Ìïú ϵúÏÝÅÌôîΕº ÏàòÌñâÌïòÍ∏∞ ÏúÑÌï¥ÏÑú ÏúÑÏùò Îѧ Í∞ÄÏßÄ ÏѧÍ≥Ñ Î≥ÄÏàòÎì§ÏùÑ Fig. 3Í≥º Í∞ôÏù¥ ÏúÝÏÝÑÏûê ÌòïÌÉúΰú Ï∞®Î°ÄÎåÄΰú 48Í∞ú(Ïû•ÎπÑ Í∞úÏàò 12Í∞ú √ó Î≥ÄÏàò Í∞úÏàò 4Í∞ú)ΰú Î∞∞Ïó¥ÌïòÏòÄÏúºÎ©∞, Ïù¥ÏßÑÌëúÌòÑÏùÑ Í∏∞Î≥∏ Î∞îÌÉïÏúºÎ°ú ÌïòÎäî ÏúÝÏÝÑÏûêÏïåÍ≥Ýζ¨Ï¶ò(Moon, 2003)Ïóê ÏÝÅÌï©ÌïòÎèÑΰù Ïó∞ÏÜçÎ≥ÄÏàòΕº Ïù¥ÏßÑÌôî ÌïòÏòÄÎã§.
3.2 ÏÝúÏïΩ Ï°∞ͱ¥
Ï∏µ ͵¨Ï°∞Ïùò Í∞ëÌåêÏóê 12Í∞úÏùò Ïû•ÎπÑÎì§ÏùÑ Î∞∞ÏπòÌïòΩ∞, Í∞ëÌåêÏùò ÌŨÍ∏∞Îäî Í∞Äΰú ÏÑ∏ΰú 20mΰú Í∞ôÏùÄ ÏÝïÏǨÍ∞ÅÌòï Ι®ÏñëÏù¥Îã§. Ïù¥Îü¨Ìïú Í∞ëÌåê ÏúÑÏóê Ïû•ÎπÑΕº Î∞∞ÏπòÌïÝ ÎïåÏùò Í∞ÄÏÝï ÏǨÌï≠ÏùÄ Îã§ÏùåÍ≥º Í∞ôÎã§. (1) Ïû•ÎπÑÏùò Î≥¥Ïàò Î∞è Í¥Äζ¨Î•º ÏúÑÌïòÏó¨ ÏÑúΰú 1.9m Ïù¥ÏÉÅ Îñ®Ïñ¥ÏÝ∏ÏÑú Í¥Äζ¨ÏûêÍ∞Ä ÏßÄÎÇòÎã§Îãê Ïàò ÏûàÏñ¥Ïïº ÌïòΩ∞, (2) Í∞ëÌåêÏùò Í∞ÄÏû•Ïûêζ¨Î°úÎ∂ÄÌÑ∞ 2m Ïù¥ÏÉÅ Îñ®Ïñ¥ÏÝ∏ ÏûàÏñ¥Ïïº ÌïúÎã§. ÎòêÌïú, Ι®Îìà ÏÝÑÏ≤¥ÏôÄ Î∞∞Ïùò Ψ¥Í≤å ÏïàÏÝïÏѱÏùÑ ÏúÑÌï¥ (3) Ïû•ÎπÑ ÏÝÑÏ≤¥Ïóê ÎåÄÌïú Ψ¥Í≤åϧëÏã¨ÏùÄ Í∞ëÌåê ÏúÑ x, yÌèâΩ¥Ïùò ϧëÏã¨ÏÝêÏóêÏÑú 1m2Ïù¥ÎÇ¥Ïóê ÏúÑÏπòÌï¥Ïïº ÌïúÎã§. ÏúÝÏÝÑÏûê ÏïåÍ≥Ýζ¨Ï¶òÏùÑ ÌܵÌï¥ ÏµúÏÝÅÌôîΕº ÏßÑÌñâÌïÝ Îïå, ÏúÑÏùò ÏÑ∏ Í∞ÄÏßÄ Ï°∞ͱ¥ÏùÑ ÎßåÏ°±ÌïòÏßÄ ÏïäÎäî Í∞úÏ≤¥Îäî Ι©ÏÝÅÌï®ÏàòÏùò Í∞íÏù¥ 1010ÏúºÎ°ú ÌŨÍ≤å ÎêòÍ≤å ÌïòÏó¨ ÌååÎÝàÌÜÝ ÏµúÏÝÅÌï¥ÏóêÏÑú ÎèÑÌÉúÎêòÎèÑΰù ÌïòÏòÄÎã§.
3.3 ÌååÏù¥ÌîÑ ÏÉùÏÇ∞Ïѱ Ι©ÏÝÅÌï®Ïàò
ÌååÏù¥ÌîÑÎäî Fig. 2Ïùò Ïû•ÎπÑ Í∞Ñ Í≥µÏÝï ÌùêζÑÏóê Îî∞Îùº Ïó∞Í≤∞ÎêòΩ∞, Í∞Å Ïû•ÎπÑÏùò ϧëÏ㨠Í∞Ñ ÏµúÎã®Í±∞ζ¨Î°ú Ïó∞Í≤∞ÎêòÎäî Í≤ÉÏù¥ ÏïÑÎãå x, y, z Îß®Ìï¥Ìäº Í±∞ζ¨ ÌòïÌÉúΰú ÏÑ∏ Î∞©Ìñ•ÏúºÎ°ú Í∫æÏó¨ Ïó∞Í≤∞ÎêúÎã§. Í≥µÏÝï Ïû•ÎπÑÏùò Ïö¥ÏÝÑÏ°∞ͱ¥ÏùÄ Table 2ÏôÄ Í∞ôÏúºÎ©∞, FPSO ÌîÑΰúÏÝùÌä∏Ïùò ÌäπÏѱ ÏÉÅ ÏúÝÏÝïÌôòÍ≤Ω, ÏÑÝÏ£ºÏùò ÏÑÝÌò∏ÎèÑÏóê Îî∞Îùº Ïó¨Îü¨ Í∞ÄÏßÄ Ï¢ÖΕòÏùò ÌååÏù¥ÌîÑÍ∞Ä ÏѧÏπòÎêòÎäî Í≤ÉÏùÑ Í≥ÝÎݧÌïòÏó¨, ÏѧÏπòÎêÝ ÌååÏù¥ÌîÑÏóê ÎåÄÌïú ÎπÑÏö©ÏùÑ Îã®ÏúÑÍ∏∏Ïù¥ Îãπ ÏÉÅÎåÄÎπÑÏö©ÏúºÎ°ú Í∞ÄÏÝïÌï®ÏúºÎ°úÏç® ÏÉÅÎåÄÏÝÅÏù∏ ÎπÑ͵êΕº Í∞ÄÎä•ÌïòÍ≤å ÌïòÏòÄÎã§. CcÎäî Îã®ÏúÑ Í∏∏Ïù¥ Îãπ ÌååÏù¥ÌîÑÏùò ÏѧÏπòÎπÑÏö©, ChÎäî ÏàòÌèâ ÌååÏù¥ÌîÑÏóêÏÑúÏùò Îã®ÏúÑ Í∏∏Ïù¥ Îãπ ÌéåÌîÑÎπÑÏö©, CdÎäî ÏàòÏßÅ ÌååÏù¥ÌîÑÏóêÏÑú ÎÇ¥Î∂ÄÏúÝÎèôÏù¥ ÌïòÍ∞ïÌïòÎäî Í≤ΩÏö∞Ïóê Îã®ÏúÑ Í∏∏Ïù¥ Îãπ ÌéåÌîÑÎπÑÏö©, CuÎäî ÏàòÏßÅ ÌååÏù¥ÌîÑÏóêÏÑú ÎÇ¥Î∂ÄÏúÝÎèôÏù¥ ÏÉÅÏäπÌïòÎäî Í≤ΩÏö∞Ïóê Îã®ÏúÑ Í∏∏Ïù¥ Îãπ ÌéåÌîÑÎπÑÏö©ÏùÑ ÎÇòÌÉÄÎǥΩ∞ Ï≤®Ïûê i, jÎäî Ïû•ÎπÑ i, jÍ∞ÑÏùò Ïó∞Í≤∞ÏùÑ ÎÇòÌÉÄÎÇ∏Îã§. Ïó∞Í≤∞Îêú ÌååÏù¥ÌîÑÏùò Í∏∏Ïù¥Îäî Ïãù (1)Í≥º Í∞ôÏù¥ Ïó∞Í≤∞Îêú Ïû•ÎπÑÎì§Ïùò ϧëÏ㨠ϢåÌëú x, y, zÏùò Ï∞®Ïù¥ Í∞íÍ≥º Í∞ôÎã§. Ïãù (2)Îäî ÌååÏù¥ÌîÑ ÏѧÏπò Ι©ÏÝÅÌï®ÏàòÏù∏ FcΕº ÎÇòÌÉÄÎǥΩ∞ CvÎäî ÎÇ¥Î∂ÄÏúÝÎèôÏù¥ ÏÉÅÏäπÏù¥Î©¥ Cu, ÌïòÍ∞ïÏù¥Î©¥ CdÏùò Í∞íÏùÑ Í∞ÄÏßÑÎã§.

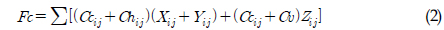
3.4 ÌôîÏû¨ ÏúÑÌóòÎèÑ Î™©ÏÝÅÌï®Ïàò
ÏùºÎ∞òÏÝÅÏúºÎ°ú ÏúÑÌóòÎèÑΕº Í≥ÝÎݧÌïú ÏѧÍ≥ÑÏóêÎäî ϵúÏïÖÏùò ÏÉÅÌô©ÏùÑ Í∞ÄÏÝïÌïòÏó¨ Ïù¥Î•º Í≤¨ÎîîÎäî ÏѧÍ≥ÑΕº ÌïòÏßÄÎßå, Ìï¥ÏñëÌîåÎûúÌä∏ÏóêÏÑú ÏùºÏñ¥ÎÇòÎäî ÏǨÍ≥ÝÎäî ϵúÏïÖÏùò Í≤ΩÏö∞ ÌîåÎûúÌä∏ ÏÝÑÏ≤¥Í∞Ä ÏÝÑÏÜåÌïòÎäî ÌÅ∞ ÏǨÍ≥Ýΰú Ïù¥Ïñ¥ÏßÄÍ∏∞ ÎïåΨ∏Ïóê ÌïòÎÇòÏùò Ι®Îìà ÎÇ¥Î∂ÄÏóê ÎåÄÌï¥ÏÑú ÏúÑÌóòÎèÑΕº ÎÖºÌïòÍ∏∞Í∞Ä Ïñ¥ÎݵÎã§. Îî∞ÎùºÏÑú Ïù¥Î≤à Ïó∞͵¨ÏóêÏÑúÎäî 100Î≤àÏùò ÏǨÍ≥ÝÍ∞Ä ÏùºÏñ¥ÎǨÎã§Í≥Ý Í∞ÄÏÝïÌïòÏó¨, Í∑∏ϧë Í∞ÄÏû• ÏúÑÌóòÌïú ÏÉÅÌô©Ïóê ÎåÄÌïòÏó¨ ÏúÑÌóòÎèÑΕº ÌèâÍ∞ÄÌïòÏòÄÎã§.
3.4.1 ÏãúÎÇòζ¨Ïò§ ÏÑÝÏÝï
Í≥µÏÝï Ïû•ÎπÑÏùò ÌôîÏû¨, Ìè≠Î∞úÌï¥ÏÑùÏùÑ ÌïÝ Îïå Ìï¥ÏÑùÍ≤∞Í≥ºÏóê Ï£ºÏöîÌïòÍ≤å ÏûëÏö©ÌïòÎäî ÏöîÏù∏Îì§ÏùÄ ÏǨÍ≥ÝÍ∞Ä ÏùºÏñ¥ÎÇú ÏïïÎÝ• Ïö©Í∏∞ ÎÇ¥Î∂ÄÏùò ΨºÏßà ͵¨ÏѱÍ≥º Ïö¥ÏÝÑ Ï°∞ͱ¥, ÌååÍ≥µÌŨÍ∏∞, ÎàÑÏ∂úÏù¥ ÏßÄÏÜçÎêú ÏãúÍ∞Ñ, Î∞îÎûåÏùò ÏÑ∏Í∏∞Í∞Ä ÏûàÎã§. Í≥µÏÝï Ïû•ÎπÑ ÎÇ¥Î∂ÄÏùò Í≥µÏÝï ΨºÏßàÏùÄ Í∞ÄÏä§ ÎÉâÍ∞ÅÍ∏∞Ïùò Í≤ΩÏö∞ ΩîÌÉÑÏù¥ 0.6, ÏóêÌÉÑ, ÌîÑΰúÌåê, Î∂ÄÌÉÑÏù¥ Í∞ÅÍ∞Å 0.1Ïù∏ ÎπÑÏú®Î°ú 2,000kgÏù¥Î©∞, Ïä§ÌŨÎü¨Î≤ÑÏôÄ Í∞ÄÏä§ÏïïÏ∂ïÍ∏∞Îäî ΩîÌÉÑÏù¥ 0.8, ÏóêÌÉÑÏù¥ 0.2Ïùò ÎπÑÏú®Î°ú Í∞ÅÍ∞Å 2,000kgÍ≥º 1,000kgÏù¥ Îì§Ïñ¥ÏûàÎã§Í≥Ý Í∞ÄÏÝïÌïòÏòÄÎã§.
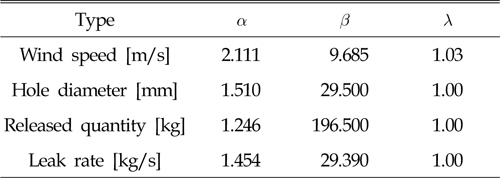
Î≥∏ Ïó∞͵¨ÏóêÏÑúÎäî ÌíçÏÜç, ÌååÍ≥µÌŨÍ∏∞, ÎàÑÏ∂ú ÏãúÍ∞ÑÏùò ÏÑ∏ Í∞ÄÏßÄ ÏöîÏù∏Ïóê ÎåÄÌï¥ ÏǨÍ≥Ý ÏãúÎÇòζ¨Ïò§Î•º ÏÑÝÏÝïÌïòÏòÄÎã§. ÎàÑÏ∂ú ÏãúÍ∞ÑÏùÑ Íµ¨ÌïòÍ∏∞ ÏúÑÌïòÏó¨ Yu(2010)Ïùò ÏÉòÌîå ÏûêΣåΕº ÌÜÝÎåÄΰú Ïó∞ΣåÏùò ÎàÑÏ∂ú ÏÜçÎèÑÏôÄ ÎàÑÏ∂ú ÏñëÏùò ÌôïΕÝÏÝÅ ÌäπÏѱÏùÑ ÏÝïÏùòÌïòÏòÄÎã§. ÌíçÏÜçÏùÄ Î∂ÅÌï¥ÏßÄÏó≠Ïùò ÌíçÏÜç Îç∞Ïù¥ÌÑ∞Εº ÌÜÝÎåÄΰú ÌôïΕÝÎ∂ÑÌè¨Ìï®ÏàòΕº ÏÝïÏùòÌïòÏòÄÍ≥Ý(HSE, 2001), ÌååÍ≥µÌŨÍ∏∞Ïóê ÎåÄÌïú ÌôïΕÝÎ∂ÑÌè¨Ìï®ÏàòÎäî FPSOÏùò ÏǨÍ≥Ý Îç∞Ïù¥ÌÑ∞(DNV, 2009)Εº ÌÜÝÎåÄΰú ÏûëÏѱÎêòÏóàÎã§. Ι®ÎìÝ ÌôïΕÝÎ∂ÑÌè¨Ìï®ÏàòÎäî ÏãÝ΢∞ÏѱÍ≥µÌïô, ÏÇ∞ÏóÖ/ÏÝúÏ°∞Í≥µÌïô, Í∏∞ÏÉÅÏòàÎ≥¥ Îì± Î∂ÑÏïºÏóêÏÑú ÏǨͱ¥Î∞úÏÉù ÌôïÎ•Ý Îì±ÏùÑ Ïûò ÌëúÌòÑÌï¥Ï£ºÎäî ÏôÄÏù¥Î∏î Î∂ÑÌè¨(Weibull distribution)ÌòïÌÉúΰú Í∑ºÏǨÌïòÏòÄÏúºÎ©∞, Ïãù (3)ÏùÄ ÏôÄÏù¥Î∏î Î∂ÑÌè¨Î•º ÎÇòÌÉÄÎÇ∏Îã§. Table 4Îäî ÌíçÏÜç, ÌååÍ≥µÌŨÍ∏∞, ÎàÑÏ∂ú Ïñë, ÎàÑÏ∂úÏÜçÎèÑÏóê ÎåÄÌïú ÏôÄÏù¥Î∏î Î∂ÑÌè¨Ïùò Í≥ÑÏàòÏù¥Î©∞ Í∞ÄΰúÏ∂ï(xÏ∂ï)Ïùò Îã®ÏúÑÎäî Ï∞®Î°Äΰú m/s, mm, kg, kg/sÏù¥Îã§.
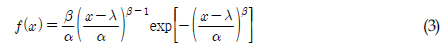
Ïù¥ÏôÄ Í∞ôÏù¥ ÏñªÏùÄ 4Í∞ÄÏßÄ ÌôïΕÝÎ∂ÑÌè¨Ìï®ÏàòÏóê ÎåÄÌï¥ Î™¨ÌÖåÏπ¥Î•ºÎ°ú ÏãúÎƨÎÝàÏù¥ÏÖòÏùÑ ÏàòÌñâÌïòÏó¨ 100Í∞ÄÏßÄ ÌëúÎ≥∏ÏùÑ Ï∂îÏ∂úÌïòÏòÄÍ≥Ý, Í∑∏ ϧë ÎàÑÏ∂ú ÏñëÏóê ÎàÑÏ∂ú ÏÜçÎèÑΕº ÎÇòÎàÑÏñ¥ÏÑú ÎàÑÏ∂ú ÏãúÍ∞ÑÏùò ÌëúÎ≥∏ÏùÑ Íµ¨ÌïòÏòÄÎã§. Î∞îÎûåÏùòÏÑ∏Í∏∞, ÌååÍ≥µÌŨÍ∏∞, Ïó∞ΣåÏùò ÎàÑÏ∂ú ÏãúÍ∞ÑÏùò ÏÑ∏ Í∞ÄÏßÄ ÏöîÏÜåΰú Ïù¥Î£®Ïñ¥ÏßÑ 100Í∞ÄÏßÄÏùò Í∞ÄÎä•Ïѱ ÎÜíÏùÄ ÏǨÍ≥Ý ÏãúÎÇòζ¨Ïò§Î•º ÏÑÝÏÝïÌïú ÌõÑ, Ïù¥Î•º DNV-Phast 7.0ÏúºÎ°ú Ìï¥ÏÑùÌïòÏó¨ Ìï¥ÏñëÌîåÎûúÌä∏ ÌôîÏû¨ÏǨÍ≥ÝÏóêÏÑú ÌùîÌïòÍ≤å ÏùºÏñ¥ÎÇòÎäî Jet fireΕº Í∏∞ϧÄÏúºÎ°ú Í∞ÄÏû• ÌîºÌï¥Í∞Ä Ïã¨Ìïú ÏãúÎÇòζ¨Ïò§ ÌïòÎÇòΕº Í≤∞ÏÝïÌïòÏòÄÎã§. Jet fireÎäî Ïö©Í∏∞Ïùò ÌååÏÜêÏßÄÏÝêÏóêÏÑú Í∞ÄÏó∞Ïѱ ΨºÏßàÏù¥ Í≥ÝÏÜçÏúºÎ°ú Î∂ÑÏ∂úÎêòΩ¥ÏÑú, ÏÝêÌôîÏõêÍ≥º ÎãøÏïÑ Í∞ÄÏó∞Ïѱ ΨºÏßàÏùò Î∂ÑÏ∂úÏù¥ ΩàÏ∂îÏßÄ ÏïäÎäî Ìïú, ÌôîÏû¨Í∞Ä ÏßÄÏÜçÏÝÅÏúºÎ°ú ÏúÝÏßÄÎêòÎäî ÌäπÏßïÏùÑ Í∞ÄÏßÄÎäî ÌôîÏû¨Ïù¥Îã§. Î≥∏ Ïó∞͵¨ÏóêÏÑú Í≤∞ÏÝïÌïú Í∞ÄÏû• Ïã¨Í∞ÅÌïú ÏãúÎÇòζ¨Ïò§Ïùò Jet fireÎäî ÌíçÏÜç 7.97m/s, ÌååÍ≥µÌŨÍ∏∞ 91.50mm, ÎàÑÏ∂ú ÏãúÍ∞Ñ 24.29sÏù∏ Í≤ΩÏö∞ΰú ÎÇòÌÉÄÎǨÎã§.
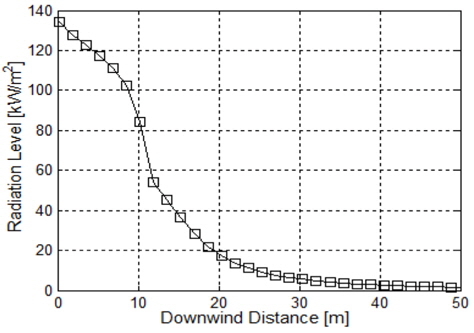
ÏÑÝÏÝïÎêú ÏãúÎÇòζ¨Ïò§ÏóêÏÑú Í∞Å Ïû•ÎπÑÏóê ÌôîÏû¨ Î∞úÏÉù Ïãú ͱ∞ζ¨Ïóê Îî∞Ε∏ Î≥µÏǨÏó¥ÏùÑ Ïû•ÎπÑÎ≥Ñΰú Í≥ÑÏÇ∞ÌïòÏòÄÎã§. Fig. 4Îäî ÌôîÏû¨ ÏòÅÌñ•Ïù¥ Í∞ÄÏû• Ïã¨Ìïú ÏãúÎÇòζ¨Ïò§ÏóêÏÑú Í∞ÄÏä§ÎÉâÍ∞ÅÍ∏∞Ïùò ÌôîÏû¨ Î∞úÏÉù Ïãú ͱ∞ζ¨Ïóê Îî∞Ε∏ Î≥µÏǨÏó¥ÎüâÏù¥Îã§.
3.4.2 화재 위험도 계산
ÌôîÏû¨ Î∞úÏÉù Ïãú Ïù∏ÏÝëÏû•ÎπÑÍ∞Ä Î∞õÎäî ÏòÅÌñ•ÏùÄ ÌôîÏû¨ ÎãπÏãú ÌíçÌñ•Ïóê ÏùòÌï¥ Í∞ÄÏû• ÌŨÍ≤å Ï¢åÏö∞ÎêúÎã§. Îî∞ÎùºÏÑú Í∞ÄÏû• Ïã¨Ìïú ÌîºÌï¥Î•º Í≥ÝÎݧÌïòÍ∏∞ ÏúÑÌïòÏó¨ ÏïûÏÑú ͱ∞ζ¨Ïóê Îî∞Ε∏ Î≥µÏǨÏó¥ÎüâÏùÑ Î∞îÎûåÏù¥ Î∂àÏñ¥Í∞ÄÎäî Î∞©Ìñ•ÏúºÎ°ú Í≥ÑÏÇ∞ÌïòÏòÄÍ≥Ý, Î∞îÎûåÏù¥ Î∂àÏñ¥Ïò§Îäî Î∞©Ìñ•Ïóê Îî∞Îùº Í∑∏ ÏòÅÌñ•Ïù¥ Ï£ºÎ≥ÄÏû•ÎπÑÏóê ÎØ∏ÏπúÎã§Í≥Ý Í∞ÄÏÝïÌïòÏòÄÎã§. Î∞îÎûåÏù¥ ÌäπÏÝï Î∞©Ìñ•Ïóê Îî∞Îùº Î∂àÏñ¥Ïò¨ ÌôïΕÝÏùÄ Î∂ÅÌï¥ÏßÄÏó≠Ïùò Îç∞Ïù¥ÌÑ∞Εº ÏǨÏö©ÌïòÏòÄÎã§.
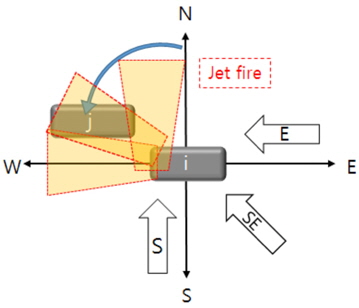
ÎòêÌïú ÌôîÏû¨Í∞Ä Fig. 5ÏôÄ Í∞ôÏù¥ Î∞úÏÉùÌïú Ïû•ÎπÑ iΕº ϧëÏã¨ÏúºÎ°ú Ïù∏ÏÝëÏû•ÎπÑ jÍ∞Ä Î∂ÅÏÑúÏ™ΩÏóê ÏûàÏùÑ Í≤ΩÏö∞, Ïù∏ÏÝëÏû•ÎπÑÍ∞Ä ÏòÅÌñ•ÏùÑ Î∞õÎäî Î∞îÎûåÏùÄ ÎÇ®ÎèôÌíçÎßåÏù¥ ÏïÑÎãàÎùº ÎÇ®ÌíçÍ≥º ÎèôÌíçÏùò ÏòÅÌñ•ÏùÑ ÎèôÏãúÏóê Î∞õÏúºÎ©∞, Ïù¥Ïóê ÏùòÌïú ÏòÅÌñ•ÎèÑΕº Ι®Îëê Í≥ÝÎݧÌïòÏòÄÎã§.
Ïù¥Î•º ÏàòÏπòÏÝÅÏúºÎ°ú ÌëúÌòÑÌïòÍ∏∞ ÏúÑÌï¥ ÌôîÏû¨ Î∞úÏÉùÏû•ÎπÑΕº ÏõêÏÝêÏúºÎ°ú Ïù∏ÏÝëÏû•ÎπÑÍ∞Ä ÏúÑÏπòÌïú Î∞©Ìñ•Ïóê Îî∞Îùº Î∞îÎûåÏùò ÏòÅÌñ•Ïóê ÎåÄÌïú ÌçºÏßÄÏÜåÏÜçÎèÑ Ìï®ÏàòΕº Fig. 6Í≥º Í∞ôÏù¥ ÎèÑÏ∂úÌïòÏòÄÏúºÎ©∞, Ìï¥Îãπ Í∑∏ÎûòÌîÑ ÏôºÏ™ΩÏóêÏÑúÎ∂ÄÌÑ∞ ÎÇ®Ìíç, ÎÇ®ÎèôÌíç, ÎèôÌíç, Î∂ÅÎèôÌíçÏùò ÏàúÏÑúΰú ÏѧÏÝïÌïòÏó¨ ÌíçÌñ•Ïóê Îî∞Îùº Ïû•ÎπÑÍ∞Ä Î∞õÎäî ÌôîÏû¨Ïùò ÏòÅÌñ•ÏùÑ ÏÝïÎèÑ ÎÜíÍ≤å Í≥ÝÎݧÌïÝ Ïàò ÏûàÎèÑΰù ÌïòÏòÄÎã§. ÌçºÏßÄ ÏÜåÏÜçÎèÑÌï®ÏàòÎäî ÏùºÎ∞òÌôîÎêú Ï¢Ö Î™®ÏñëÏúºÎ°ú ÏѧÏÝïÌïòÏó¨ Ìè≠ ÎÑìÏùÄ ÌëúÌòÑÏùÑ Í∞ÄÎä•ÌïòÍ≤å ÌïòÏòÄÏúºÎ©∞, Ι®ÎìÝ ÏÝêÏóêÏÑú 0Ïù∏ Î∂ÄÎ∂ÑÏùÑ ÏóÜÍ≤å ÌïòÏó¨ ÏÜåÏÜçÎèÑ ÎòêÌïú ÏÝÅÏÝàÌïòÍ≤å ÎÇòÌÉÄÎǺ Ïàò ÏûàÍ≤å ÌïòÏòÄÎã§. ÏùºÎ∞òÌôîÎêú Ï¢Ö Î™®ÏñëÏùÄ ÌååÎùºÎØ∏ÌÑ∞ a, b, cΕº Î∞îÌÉïÏúºÎ°ú Ïãù (4)ΰú ÌëúÌòÑÎêúÎã§.

ÌôîÏû¨ ÏúÑÌóòÎèÑÏùò Ι©ÏÝÅÌï®Ïàò FrÏùÄ ÌôîÏû¨Í∞Ä Î∞úÏÉùÌïú Ïû•ÎπÑ iÍ∞Ä Ïù∏ÏÝëÏû•ÎπÑ jÏóêÍ≤å ÎØ∏ÏπòÎäî Î≥µÏǨÏó¥ÎüâÏùò Ï¥ùÌï©Ïù¥Î©∞, Îëê Ïû•ÎπÑÍ∞Ä Í∞ôÏùÄ Ï∏µÏóê ÏûàÏùÑ Í≤ΩÏö∞Îäî Ïãù (4)ÏôÄ Í∞ôÎã§. Îëê Ïû•ÎπÑÍ∞Ä Îã§Î•∏ Ï∏µÏóê ÏûàÏùÑ Í≤ΩÏö∞ÏóêÎäî Í∑∏ ÏòÅÌñ•Ïù¥ 1/2ΰú ϧÑÏñ¥ÎìÝÎã§Í≥Ý Í∞ÄÏÝïÌïòÏòÄÏúºÎ©∞ Ïù¥ÎïåÎäî Ïãù (5)Εº Îî∞Ε∏Îã§. MÏùÄ Ïû•ÎπÑ jÏùò ÌäπÏÝï ÌíçÌñ•Ïóê ÎåÄÌïú ÏÜåÏÜçÎèÑÏù¥Î©∞ PW Îäî Î∞©Ìñ•Ïóê Îî∞Îùº Î∞îÎûåÏù¥ Î∂àÏñ¥Ïò¨ ÌôïΕÝ, RÏùÄ ÏïûÏÑú Î∞îÎûåÏù¥ Î∂àÏñ¥Í∞ÄÎäî Î∞©Ìñ•ÏúºÎ°ú Í≥ÑÏÇ∞Îêú ÌôîÏû¨Ïû•ÎπÑ iÏôÄ Ïù∏ÏÝëÏû•ÎπÑ jÏǨÏù¥Ïùò ͱ∞ζ¨Ïóê Îî∞Ε∏ Î≥µÏǨ Ïó¥ÎüâÏù¥Îã§.


3.5 배치 결과
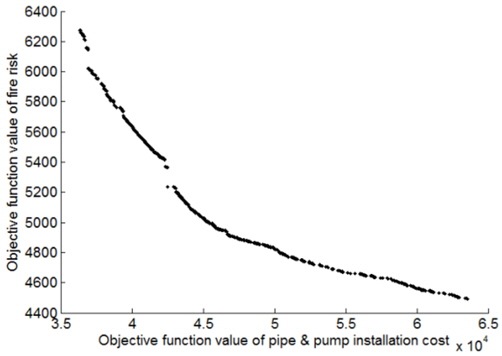
MatlabÏóê ÎÇ¥Ïû•ÎêòÏñ¥ ÏûàÎäî Îã§Î™©ÏÝÅ ÏúÝÏÝÑÏûê ÏïåÍ≥Ýζ¨Ï¶ò(The Math Works, 2010)ÏùÑ Ïù¥Ïö©ÌïòÏó¨ ÌååÏù¥ÌîÑ ÏѧÏπòÏôÄ ÌôîÏû¨ ÏúÑÌóòÎèÑÏóê Í¥ÄÎÝ®Ìïú Îëê Í∞ÄÏßÄ Î™©ÏÝÅÌï®ÏàòÏóê ÎåÄÌïú ÌååÎÝàÌÜÝ ÏµúÏÝÅÏùÑ ÌÉêÏÉâÌïòÏòÄÎã§. ϵúÏÝÅÎ∞∞Ïπò Ψ∏ÏÝúÎäî Ï¢ÅÏùÄ Í≥µÍ∞ÑÏóê ÎßéÏùÄ ÏàòÏùò Ïû•ÎπÑÍ∞Ä Îì§Ïñ¥Í∞ÄÎØÄΰú ÏÝúÌïúÏ°∞ͱ¥ÏùÑ ÎßåÏ°±ÌïòÎäî Î∞∞ÏπòÏóêÏÑú Ï°∞Í∏àÎßå Ïû•ÎπÑÏùò ÏúÑÏπòÍ∞Ä Î∞îÎÄåÏñ¥ÎèÑ ÏÝúÌïúÏ°∞ͱ¥ÏùÑ ÎßåÏ°±ÌïòÏßÄ Î™ªÌïòÍ≤å ÎêòÎäî Í≤ΩÏö∞Í∞Ä ÎßéÎã§. Í∑∏Îü¨ÎØÄΰú ÏÝúÌïúÎêú Í≥µÍ∞ÑÏóêÏÑú Ïû•ÎπÑÏùò ϵúÏÝÅÎ∞∞ÏπòΕº Ï∞æÎäî Ψ∏ÏÝúÏóê ÏúÝÏÝÑÏûê ÏïåÍ≥Ýζ¨Ï¶òÏùÑ Ïù¥Ïö©ÌïòÎäî Í≤ΩÏö∞ ͵≠ÏÜå ϵúÏÝÅÌï¥(Local minimum)Ïóê ÎπÝÏßÄÍ∏∞ ÏâΩÍ≥Ý, ϵúÏÝÅÌï¥Í∞Ä ÏúÝÏÝÑÏûêÏùò Ï¥àÍ∏∞ Í∞íÏóê Îî∞Îùº ÌŨÍ≤å Ï¢åÏö∞ÎêòÎäî Ψ∏ÏÝúÍ∞Ä ÏûàÎã§. Îî∞ÎùºÏÑú ÏùºÎ∞òÏÝÅÏúºÎ°ú ÎèåÏó∞Î≥ÄÏù¥(Mutation)Ïùò Î∞úÏÉù ÌôïΕÝÏùÑ 0.02ÏÝïÎèÑΰú ÏѧÏÝïÌïòÎäîÎç∞ ÎπÑÌïòÏó¨ Î≥∏ Ïó∞͵¨ÏóêÏÑúÎäî 0.1ΰú ÌŨÍ≤å ÎäòÎݧÏÑú ϵúÏÝÅ Ìï¥Î•º ÌÉêÏÉâÌïòÏòÄÏúºÎ©∞, Î∞∞Ïπò ÌòïÌÉúΕº Îã§ÏñëÌïòÍ≤å ÏÉùÏѱÌïòÍ∏∞ ÏúÑÌï¥ Ï¥àÍ∏∞ ÏßëÎã®Ïùò Ïû•ÎπÑ ÏúÑÏπòÏóê ÎåÄÌïú ÏѧÍ≥ÑÎ≥ÄÏàòÎäî ÏûÑÏùòÏùò Í∞íÏúºÎ°ú ÏѧÏÝïÌïòÏòÄÎã§. Fig. 7ÏùÄ 3,000Í∞úÏùò Ι®ÏßëÎã® ÏúÝÏÝÑÏûêΕº 1,000ÏÑ∏ÎåÄÏóê ͱ∏Ï≥ê ÏßÑÌôîÏãúÌǧΩ¥ÏÑú Ï∞æÏùÄ ÌååÎÝàÌÜÝ ÏµúÏÝÅÌï¥Î•º ÌååÏù¥ÌîÑ, ÌéåÌîÑ ÏѧÏπòÎπÑÏö©Í≥º ÏúÑÌóòÎèÑΕº Ï∂ïÏúºÎ°ú ÌïòÏó¨ ÎÇòÌÉÄÎÇ¥ÏóàÎã§.
ÌååÏù¥ÌîÑ ÏÉùÏÇ∞ÏѱÍ≥º ÌôîÏû¨ ÏúÑÌóòÎèÑÏùò ϧëÏöîÎèÑÏóê Îî∞Îùº Í∞ÄϧëÏπòΕº ÏѧÏÝïÌï®ÏúºÎ°úÏç® ÏÑÝÏÝïÎêú ÌååÎÝàÌÜÝ ÏµúÏÝÅÌï¥ Ï§ëÏóêÏÑú ÏѧÍ≥ÑÏûêÍ∞Ä Ìï¥Îãπ ÌîÑΰúÏÝùÌä∏Ïóê ÏÝÅÌï©Ìïú Î∞∞ÏπòΕº ÏÑÝÌÉùÌïòÎäî Í≤ÉÏù¥ Í∞ÄÎä•ÌÜÝΰù Ìï¥Ï§ÄÎã§. ÏòàΕº Îì§Ïñ¥ ÌååÏù¥ÌîÑ ÏÉùÏÇ∞ÏѱÍ≥º ÌôîÏû¨ ÏúÑÌóòÎèÑΕº 8:2Ïùò ÎπÑϧëÏúºÎ°ú ÏѧÏÝïÌïòÏó¨ ÌååÏù¥ÌîÑ ÏÉùÏÇ∞ÏѱÏùÑ Ï§ëÏöîÌïú ÏöîÏÜåΰú Í≥ÝÎݧÌï¥Ïïº ÌïòÎäî Í≤ΩÏö∞, ÌååÎÝàÌÜÝ ÏµúÏÝÅÏÝêÏù¥ 100Í∞ú ÏûàÏùÑ Îïå ÌååÏù¥ÌîÑ ÏÉùÏÇ∞ÏѱÏù¥ 20Î≤àÏß∏ΰú ÏûëÏùÄ ÏÝêÏùÑ ÏÑÝÌÉù ÌïÝ Ïàò ÏûàÎã§. ÏùºÎ∞òÏÝÅÏúºÎ°ú ÏÉÅÏ∂©ÌïòÎäî Îëê Ι©ÏÝÅÌï®ÏàòÏóê ÎåÄÌïú ÌååÎÝàÌÜÝ ÏµúÏÝÅÌï¥Îì§ÏùÄ Îã®Ï°∞Í∞êÏÜåÏùò ÌòïÌÉúΕº Î≥¥Ïù¥ÎØÄΰú Ïù¥Îäî ÌôîÏû¨ ÏúÑÌóòÎèÑÍ∞Ä 80Î≤àÏß∏ΰú ÏûëÏùÄ ÏÝêÍ≥º Í∞ôÎã§. Fig. 8ÏùÄ ÌååÏù¥ÌîÑ ÏÉùÏÇ∞ÏѱÍ≥º ÌôîÏû¨ÏúÑÌóòÎèÑΕº 8:2ΰú Í≥ÝÎݧÌïú Î∞∞ÏπòÏù¥Î©∞ Ι©ÏÝÅÌï®ÏàòÏùò Í∞íÏùÄ Í∞ÅÍ∞Å 39,274ÏôÄ 5,751ΰú ÌååÏù¥ÌîÑ ÏÉùÏÇ∞ÏѱÏùÑ Ï§ëÏöîÌïòÍ≤å Í≥ÝÎݧÌï®ÏúºÎ°úÏç® 1Ï∏µÍ≥º 2Ï∏µÏùò Ïû•ÎπÑÎì§ Î™®Îëê ÎπÑ͵êÏÝŠϧëÏã¨Ïóê Ι®Ïó¨ Î∞∞ÏπòÎêòÏñ¥ ÏÑúΰú Í∞ÑÏùò ͱ∞ζ¨Î•º ϧÑÏù¥Í∏∞ ÏúÑÌïú Î∞∞ÏπòÍ∞Ä Îêú Í≤ÉÏúºÎ°ú ÌåêÎã® ÌïÝ Ïàò ÏûàÎã§. ÏѧÍ≥ÑÏûêÎäî Ïù¥Îü¨Ìïú Î∞©Î≤ïÏúºÎ°ú Ïó¨Îü¨ Î∞∞Ïπò ÏïàÏùÑ Í≤ÄÌÜÝÌïòÏó¨ ÏãúÏä§ÌÖúÏùò ÌäπÏѱÏóê ÎßûÎäî ϵúÏ¢Ö Î∞∞ÏπòΕº Í≤∞ÏÝïÌïÝ Ïàò ÏûàÍ≤å ÎêúÎã§.
4. Í≤∞ ΰÝ
Î≥∏ Ïó∞͵¨ÏóêÏÑúÎäî ÌôîÏû¨ ÏúÑÌóòÎèÑΕº Í≥ÝÎݧÌïòÏó¨ Îã§Ï§ë Í∞ëÌåêÏù∏ FPSOÏùò Í≥ÝÏïïÍ∞ÄÏä§ ÏïïÏ∂ïΙ®ÎìàÏùÑ ÏúÑÌïú Ïû•ÎπÑÏùò ϵúÏÝÅÎ∞∞ÏπòΕº ÏàòÌñâÌïòÏòÄÎã§. Ïù¥Î•º ÏúÑÌï¥, ÏѧÍ≥Ñ Î≥ÄÏàòΰúÏÑú Ïû•ÎπÑÏùò ÏúÑÏπòÏôÄ Î∞∞Ïπò Î∞©Ìñ•Ïóê Í¥ÄÌïú Î≥ÄÏàòΕº ÏúÝÏÝÑÏûêÏùò ÌòïÌÉúΰú ÏÝïÏùòÌïòÏòÄÍ≥Ý, Ïû•ÎπÑÏùò ÏúÝÏßÄ Î∞è Î≥¥ÏàòÏôÄ Ïû•ÎπÑÏùò Î∞∞Ïπò ÌõÑ ÏÝÑÏ≤¥ Ι®ÎìàÏùò Ψ¥Í≤å ϧëÏ㨠ÏïàÏÝïÏѱÏùÑ Í≥ÝÎݧÌïòÏó¨ ÏÝúÌïúÏ°∞ͱ¥ÏùÑ ÏѧÏÝïÌïòÏòÄÎã§. Ïù¥Îü¨Ìïú ÏÝúÌïú Ï°∞ͱ¥ ÌïòÏóêÏÑú ÌôîÏû¨ ÏúÑÌóòÎèÑÏôÄ ÌååÏù¥ÌîÑ, ÌéåÌîÑÏùò ÏѧÏπòÎπÑÏö©ÏùÑ Îëê Í∞ÄÏßÄ Î™©ÏÝÅÌï®Ïàòΰú ÏÝïÏùòÌïòÏòÄÏúºÎ©∞, ÎçîÏö± Ïã§ÏÝúÏÝÅÏù∏ ÌôîÏû¨Ïùò ÏòÅÌñ•ÏùÑ Í∏∞ÏàÝÌïòÍ∏∞ ÏúÑÌï¥ ÌçºÏßÄ Í∞úÎÖêÏùÑ ÎèÑÏûÖÌïòÏòÄÎã§. ϵúÏ¢ÖÏÝÅÏúºÎ°úÎäî Îëê Ι©ÏÝÅÌï®ÏàòÏóê ÎåÄÌï¥ ÏúÝÏÝÑÏûê ÏïåÍ≥Ýζ¨Ï¶òÏùÑ Ïù¥Ïö©Ìïú ÌååÎÝàÌÜÝ ÏµúÏÝÅÏùÑ MATLABÏúºÎ°ú ÏàòÌñâÌïòÏòÄÍ≥Ý, Ïù¥Î•º ÌܵÌï¥ ÏѧÍ≥ÑÏûêÏùò ÏùòÎèÑΕº Î∞òÏòÅ ÌïÝ Ïàò ÏûàÎäî ϵúÏÝÅÎ∞∞Ïπò Î∞©Î≤ïÏùÑ ÏÝúÏãúÌïòÏòÄÎã§.
Ìñ•ÌõÑ, Í≥µÏÝï Ïû•ÎπÑ ÏÑ∏Î∂ÄÏÝÅÏù∏ ÌäπÏѱÏùò ÌååÏïÖ, ÌôîÏû¨ Î∞úÏÉù Ïãú Ï£ºÎ≥Ä Ïû•ÎπÑÎì§Ïóê ÏùòÌï¥ Î≥ÄÌôîÌïòÎäî ÌôîÏû¨Ïùò ÏòÅÌñ•, ÌååÏù¥ÌîÑ Ïó∞Í≤∞ Ïãú ͵¥Í≥°Î∂ÄÏôÄ ÏѧÏπò Í≤ΩΰúÏóê Îî∞Ε∏ Ïã§ÏßàÏÝÅÏù∏ ÎπÑÏö© ÏÇ∞ÏÝï, Ι®Îìà ÏÝÑÏ≤¥Ïùò Ψ¥Í≤å ÏïàÏÝïÏѱÏóê ÎåÄÌïú ÌèâÍ∞Ä ÏßÄÌëú Îì±ÏùÑ Ï∂îÍ∞ÄÌïúÎã§Î©¥ ÎçîÏö± Ïã§ÏÝúÏÝÅÏù∏ Î∞∞ÏπòϵúÏÝÅÌôîΕº ÏàòÌñâ ÌïÝ Ïàò ÏûàÏùÑ Í≤ÉÏù¥Îã§.