샘플링 기법을 통한 계류 시스템 설계 변수 최적화 방안에 관한 연구
Study on Optimization of Design Parameters for Offshore Mooring System using Sampling Method
Article information
Trans Abstract
In this study, the optimal design of a mooring system was carried out. Unlike almost all design methods, which are based on the deterministic method, this study focused on the probabilistic method. The probabilistic method, especially the design of experiment (DOE), could be a good way to cover some of the drawbacks of the deterministic approach. There various parameters for a mooring system, as widely known, including the weight, length, and stiffness of line. Scenarios for the mooring system parameters were produced using the Latin Hypercube Sampling method of the probabilistic approach. Next, a vessel-mooring system coupled analysis was performed in Orcaflex. A total of 50 scenarios were used in this study to optimize the initial design by means of a genetic algorithm. Finally, after determining the optimal process, a reliability analysis was performed to understand the system validity.
1. 서 론
계류시스템은 구조물의 설계수명 동안 환경 외력 하에서 안전하게 운영될 수 있도록 설계되어야 한다(Wang et al, 2013). 이러한 계류시스템의 안전성을 판단하는 데에는 여러 가지 상황에 따른 기준이 있으며, 계류시스템의 최적설계 및 안전성에 대한 많은 연구가 진행된 바 있다(Stendal et al., 2015; Jones and Nelson, 1982; Huang, 2000). 일반적인 계류설계 방법에서는 결정론적 방법에 의거하여 설계가 이루어져 과도한 설계가 이루어질 수 있는데, 본 연구에서 사용된 확률론적 접근 방법은 발생 가능한 경우의 수를 최대한 많이 고려하기 때문에 시스템의 높은 보수성을 보완해줄 수 있다는 장점이 있다(Sule, 2011; McTigue and Harte, 2011; Cheng and Bussel, 2001). 계류선 설계에 필요한 주요 설계 변수로는 계류선의 무게, 직경, 길이, 강성 등이 있으며, 각각의 설계 변수들은 계류 형태에 따라 계류시스템에 미치는 영향이 서로 상이할 수 있다. 목적함수를 계류선의 장력 및 부유체의 수평 이동 변위인 옵셋(Offset)이라고 했을 때, 인장강식(Taut) 계류의 경우 계류선의 무게보다 계류선의 강성이 미치는 영향이 더 커짐을 대표적으로 들 수 있다. 이처럼 계류 시스템의 구성요소들이 계류 시스템에 서로 다르게 미치는 영향을 판단하기 위해 실험계획법(DOE, Design of experiments)을 도입한 연구가 진행된 바 있으며(Ferreira et al, 2017) 이를 본 연구에 적용하였다.
2. 대상부유체 및 계류시스템
2.1 유체동역학 계수 도출
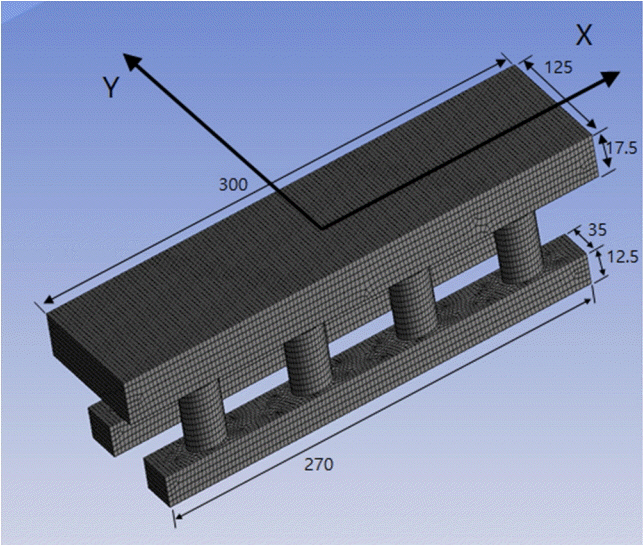
표본추출 및 최적화 해석에 앞서 대상선형의 주파수영역 운동해석을 수행하였다. 대상선형은 Fig. 1과 같은 반잠수식 구조물 형태이며, 상용프로그램인 ANSYS AQWA를 사용하여 주파수 영역에서의 거동특성을 계산하였다. ANSYS AQWA는 경계요소법(BEM, Boundary element method)을 기반으로 하여 수면 아래 선형의 표면에 배치된 각 패널에서 단위진폭을 가진 입사파에 대한 주파수별 부유체의 거동특성을 계산한다(ANSYS, 2013). 구조물의 상세 제원은 Table 1에 명시하였다.
ANSYS AQWA를 통해 계산된 유체동역학 계수는 Fig. 2와 같으며, 계산된 결과는 부유체-계류 연성해석을 위해 Orcaflex의 입력값으로 사용된다.
2.2 계류 시스템 레이아웃
본 연구에서 사용된 계류시스템은 체인-와이어-체인 형태의 현수선(Catenary) 계류시스템이다. Fig. 3과 같이 방사형 구조로 모델링 하였으며 계류시스템의 상세 제원은 Table 2에 명시하였다. 부유체-계류 연성해석은 상용프로그램인 Orcaflex로 수행하였으며, 이에 필요한 부유체의 유체 동역학적 특성들은 ANSYS AQWA를 이용하여 계산된 값을 사용하였다.

Mooring system layout (Pan et al, 2016)
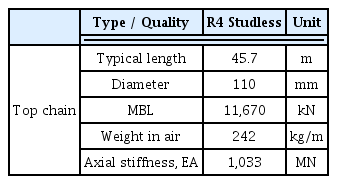
Mooring line properties (Pan et al, 2016)
해저 지형은 계류시스템 설계의 간략화 및 대칭성을 위해 편평한 바닥으로 가정하였고, 대상선형이 설치 된 지역은 남중국해 연안으로 해석에 적용된 환경조건은 Table 3과 같다. 환경하중의 방향은 180도 방향으로 동일하게 적용하였다.
3. 계류선 최적화
3.1 표본 추출
표본 추출 방법은 크게 확률론적 방법과 비 확률론적 방법으로 나눌 수 있다(Lee, 2015). 확률론적 표본 추출 방법은 대상변수의 발생확률을 확률분포함수의 형태로 가정하여 표본을 추출하는 방법으로 확률분포로 가정된 변수의 무작위 표본 추출이 가능하며 그에 따른 오차와 민감도 측정이 가능하다. 또한, 설계 변수를 확률분포로 가정하여 발생 가능한 모든 경우를 고려하기 때문에 표본추출을 통한 연구결과에 대한 신뢰도를 확보할 수 있다. 반면 비확률적 표본 추출 방법은 변수를 확률분포로 가정하지 않은 채 표본을 추출하는 방법으로 추출에 필요한 시간적인 측면에서 장점이 있다. 본 연구에서는 몇 가지의 층화추출 방법 중 몬테-카를로 샘플링(MCS, Monte carlo sampling)방법의 단점을 보완한 라틴 하이퍼큐브 샘플링(LHS, Latin hypercube sampling)방법을 사용하여 설계 변수를 추출하고(Novak et al, 2014), 설계 변수들의 조합을 통해 시나리오를 작성하였다. 완성된 시나리오 및 해석 결과를 사용하여 실험계획법을 적용하였고 최적화 해석을 수행하였다.
3.1.1 라틴 하이퍼큐브 샘플링
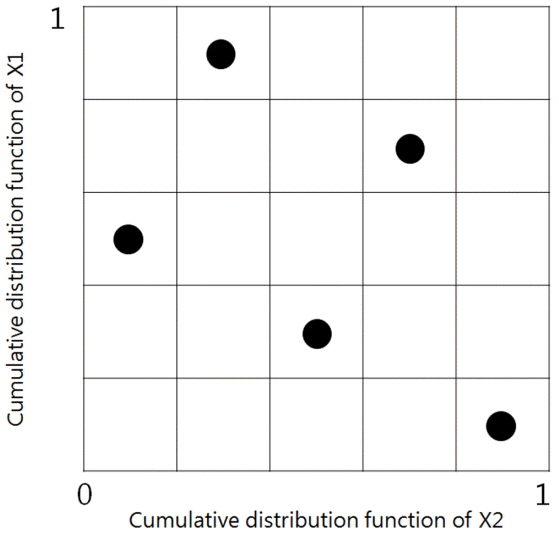
라틴 하이퍼큐브 샘플링 방법은 표본 수 및 시뮬레이션 횟수를 줄임과 동시에 정도를 높일 수 있는 방법으로 몬테-카를로 샘플링 방법의 단점을 보완한 층화추출법 중 많이 사용되는 방법이다. 라틴 하이퍼큐브 샘플링 방법은 입력변수가 적을수록 모집단의 특성을 잘 나타내주는 장점으로 표본추출방법에서 널리 이용되고 있다(Svobaba and Hilar, 2012). 예를 들어, Fig. 4와 같이 변수가 2개인 경우 각 표본 구간이 중복되지 않도록 표본을 추출할 수 있다. 각 변수는 Fig. 5와 같이 발생 확률이 같은 N개의 구간으로 구분되며 입력 변수들은 확률 분포 함수에 대해 균등하게 구간을 할당하여 동일한 1/N 발생 확률을 가지기 때문에 발생 가능한 모든 변수를 균등한 확률로 추출할 수 있다는 장점이 있다.
3.2 변수 분포
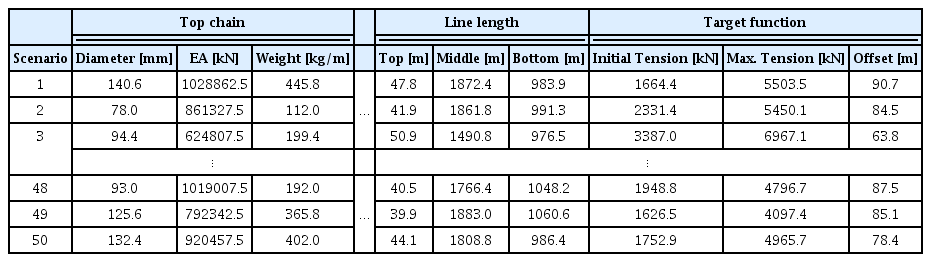
시나리오 추출을 위해 사용된 변수는 계류선의 직경, 무게, 강성, 그리고 길이이다. 체인-와이어-체인 혼합 계류시스템의 구성요소별 4가지 변수를 토대로 12변수 표본을 추출하여 50개의 시나리오를 작성하였다. 시나리오 추출을 위해 각 변수의 발생확률을 변동계수(Coefficient of variation, 표준편차/평균) 0.1을 갖는 정규분포(Normal distribution)로 가정하였으며(Bruen et al, 1991) 초기 설계안에 사용된 변수값을 정규분포의 중간값(Nominal value)으로 규정하였다. 라틴 하이퍼큐브 샘플링 방법에 의해 도출한 50개의 시나리오는 Table 4에 명시하였으며, 선정된 50개의 시나리오를 토대로 Orcaflex를 사용하여 구조물-계류시스템의 연성해석을 수행하였으며, 계류시스템의 장력과 구조물의 옵셋 등 시간 영역 해석결과를 도출하였다.
3.3 유전 알고리즘 기반 최적화
본 연구에서는 계류시스템의 높은 보수성을 보완하기 위해 최적화 해석을 수행하였으며, 최적화 과정은 유전 알고리즘에 기반을 둔다. Fig. 6에 나타낸 것과 같이 먼저 초기 설계안 표본을 바탕으로 설계 변수들의 초기 모집단을 생성한다. 이후 초기 모집단으로부터 파생된 새로운 설계변수 조합을 통해 해석 결과의 최적화 기준 수렴 여부를 판별하여 목적함수에 대한 최적 설계안을 도출하도록 표본추출 및 해석을 반복 수행하였다.
초기 모집단 생성 이후 초기 모집단의 평균, 표준편차, 최대값 및 최소값 조합을 통해 다음 모집단을 생성하며, 목적 함수에 대한 수렴도 S(모집단의 평균, 표준편차 관계를 통해 계산되는 목표수치)를 만족할 경우 즉, 식 (2)가 수렴하게 되면 Cross-over에 기반한 유전 알고리즘을 통해 2진법 체인룰(Binary chain rule)에 따라 다음 모집단을 생성한다. 본 연구에서는 모집단의 통계적 특성으로 계산된 식 (2)의 S 값이 0.02 이하가 될 때까지 반복 수행하였다.
여기서, 식 (2)에서 Mean, Max, Min, StdDev는 각각 i번째 모집단의 평균, 최대값, 최소값과 표준편차를 의미한다.
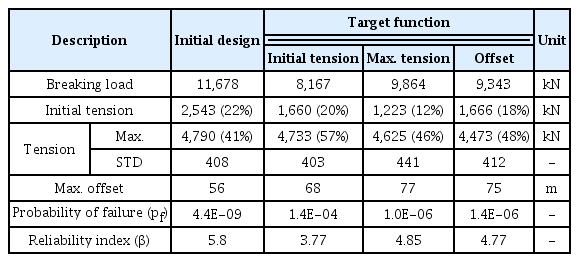
최적화는 3가지 목적함수 초기장력과 최대장력, 옵셋에 대해 수행하였으며 그 결과를 Table 5에 나타내었다. Ramnäs 및 Bridon 등 몇몇 제조사에서는 계류시스템에 사용되는 재료들의 물성치를 제공하고 있다(Brindon, 2017; Ramnäs, 2017). 최적화 결과는 위 제조사에서 제공하는 체인, 와이어의 직경, 강성 등 상세 제원을 토대로 도출되며 3가지 목적함수 공통으로 시스템의 무게감소와 성능유지를 목표로 하였다. 최적화 과정에서 시스템의 증량을 방지하기 위해 초기 설계안 대비 직경이 증가하지 않도록 하였으며, 초기장력에 대한 최적화는 50개의 시나리오 해석 결과를 바탕으로 초기장력이 파단강도의 15%를 목표로 하였으며, 최대장력에 대한 최적화는 최대 장력이 파단강도의 60%를 초과하지 않도록(API, 2005), 옵셋은 수심의 10%를 초과하지 않도록 제한조건을 선정하였다.
계류시스템 최적화 과정에서 공통으로 적용한 조건은 하단부 체인 길이 최소화이다. 최소화 범위는 초기 설계안의 해석 결과로부터 도출하였으며, 비교적 피로 강도가 약한 와이어가 해저면에 닿지 않도록 설정하였다. 초기장력을 목적함수로 하였을 때, 상단부와 하단부 체인의 직경이 각각 90mm, 87mm로 감소하였다. 최대장력을 목적함수로 한 경우 상단부, 하단부체인과 와이어의 직경은 각각 10mm, 19mm, 20mm 만큼 감소하였다. 목적함수가 옵셋일 경우 상단부 체인의 직경은 13mm, 와이어 7mm, 하단부 체인 13mm와 그에 따른 무게, 강성 등이 감소하였다. 특히, 시스템 물성치의 감소는 전반적인 시스템의 무게 감소와 직결되며 그 변화량은 Table 5에 나타난 바와 같다.
3.4. 신뢰성 평가
계류시스템 신뢰성 평가를 위해서는 먼저 계류시스템의 한계상태(Limit state)에 대한 정의가 선행되어야 한다. 한계상태란 계류시스템의 파단 상태를 견딜 수 있는 능력을 확보할 수 있는 상태 즉, 1개 이상의 계류선 파단이 일어난 상태로 정의한다(DNV, 2010). 본 연구에서 정의한 한계 상태는 계류시스템이 설계 기준, 목표 성능을 낼 수 없는 상태로 정의하여 계류선의 장력이 파단 강도를 초과한 상태로 정의하였다. 계류선의 장력이 파단강도를 초과할 확률은 식 (3)과 같다.
여기서, T는 계류선의 장력, R은 파단강도, pf 는 T가 R을 초과할 확률을 뜻한다.
통상적으로 신뢰성 평가에서는 비선형적이고 복잡한 현상을 간략화하기 위해 시스템 확률분포 및 한계상태를 독립적이고 일반화된 분포로 가정한다(Jung, 2012). 마찬가지로 본 연구에 사용된 파단강도는 변동계수 0.1을 갖는 정규분포로 가정하였고, 장력분포는 최대장력이 작용하는 계류선 장력 시계열 결과로부터 평균값과 표준편차를 계산하여 적용하였다. 계류선의 한계상태, 즉 계류선 장력이 파단강도를 초과한 상태의 분포 f(X)는 식 (3)에 따라 식 (4)과 같이 표현할 수 있으며, 정규분포를 갖는 한계상태의 확률분포 f(X)는 식 (5)과 같이 나타낼 수 있다. 또한, 식 (3)과 (5)에 따라 계류시스템의 파단확률, 즉 한계상태 분포가 0보다 낮을 확률은 식 (6)과 같다.
여기서 μX 와 σX는 각각 한계상태 분포의 평균과 표준편차, μR 과 μT 는 파단강도 및 장력 분포의 평균, σR 과 σT는 파단강도 및 장력 분포의 표준편차를 나타낸다.
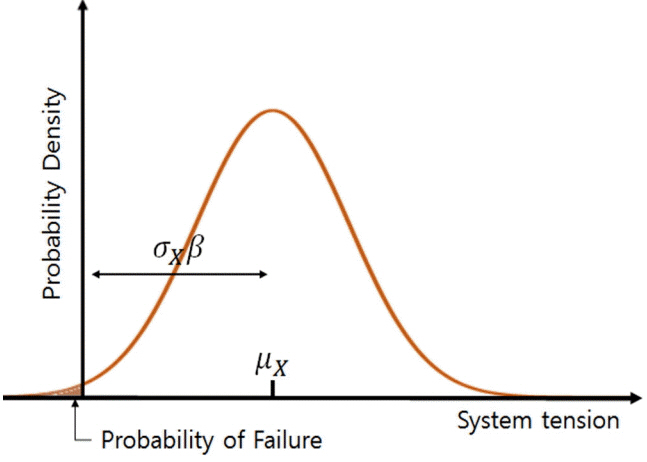
식 (6)에서 나타나는 바와 같이 신뢰성 지표 β는 발생 확률과 반비례 관계에 있다. Fig. 7에 나타난 바와 같이 한계상태의 확률밀도함수 분포에서 신뢰성 지표 및 표준편차, 평균으로부터 시스템의 파단확률을 계산할 수 있으며, 한계상태의 누적분포함수 Φ가 연속 분포일 때, 한계상태 분포가 0보다 낮을 확률은 신뢰성 지표의 함수로 표현할 수 있는데 역함수 관계에 따라 1-pf의 초과확률을 갖는 식 (7)과 같이 나타낼 수 있다.
초기 설계안에서 계산된 최대장력은 파단강도의 약 41%이며 초기장력은 약 22%이다. 수심 1,000m에서 최대 옵셋은 약 6%이며 시계열 해석 결과 도출된 신뢰성 지표값은 5.8이다. 목적함수 초기장력과 최대장력에 대한 시스템의 초기장력 변화량은 22%에서 각각 20%, 12%로 감소하였으며, 최대장력 변화량은 각각 57%, 46%로 증가하였다. 옵셋에 대한 최적화의 경우 초기장력은 18%로 4% 감소하였고, 최대장력은 48%, 최대 옵셋은 75m로 나타났다. 목적함수에 따른 시스템의 변화는 Table 6에 상세하게 나타내었다.
일반적으로 시스템 구조 안전성 측면에서 목표로 하는 신뢰성 지표는 3.0 수준이며(Joung et al., 2016), 파단확률은 약 10E-05정도이다(Ding et al., 2005). 신뢰성 지표가 높을 경우 시스템의 보수성이 높다고 볼 수 있으며, 신뢰성 지표가 낮을 경우 시스템의 안전성이 낮다고 판단할 수 있다. 본 연구에 사용된 초기 설계안의 신뢰성 지표 값은 5.8인데 반해, 목적함수가 초기장력과 최대장력, 옵셋에서는 각각 3.77과 4.85, 4.77로 감소하였다. 신뢰성 지표를 설계기준으로 삼았을 경우 초기장력을 목적함수로 하였을 때 가장 이상적인 결과를 도출하였다고 볼 수 있다. Table 4에서 초기장력과 최대장력의 %는 파단강도에 대한 초기장력비와 최대장력비를 나타내며 파단강도의 60% 즉, 안전계수 1.67을 파단으로 규정하였을 때(API, 2005) 약 57%로 가장 근접하였으며, 수심 1,000m에서 최대 옵셋은 약 7%로 수렴한다. 반면 목적함수를 최대장력, 옵셋으로 하였을 경우 시스템의 최대장력은 각각 파단강도의 약 46%, 48%이며, 최대 옵셋은 약 8%이다.
4. 결 론
본 연구에서는 초기 설계안을 바탕으로 50개의 시나리오를 작성하여 대상 해역의 환경조건에 적합한 최적화 해석을 수행하였다. 대상선형은 반잠수식 구조물이며 해당 구조물에 적용된 계류시스템을 사용하였고 남중국해 극한조건에서의 위치유지 성능을 평가하였다. 최적화의 목적함수는 초기장력과 최대장력이며, 50개의 시나리오 해석 결과를 사용하여 유전 알고리즘을 적용하였다.
초기장력을 목적함수로 하였을 경우 상단부, 하단부 체인의 직경과 무게 및 강성이 감소하였으며 그에 따른 전반적인 시스템의 무게도 감소하였다. 반면 최대장력을 목적함수로 하였을 경우 상단부 체인과 와이어 및 하단부 체인의 물성치 모두 감소하였다. 계류시스템의 무게 감소에 수반하는 초기장력의 감소는 대상선형의 운동성능 및 계류시스템 특성의 변화를 초래하기 때문에 변화량에 따른 검토가 필요하며, 파단강도와 안전계수, 대상선형의 옵셋과 신뢰성 지표를 통해 그 적정성을 평가하였다. 최적화 결과 시스템의 무게와 그에 따른 초기장력은 감소하였으며, 옵셋은 다소 증가하였다. 두 가지 목적함수에 대한 결과 모두 파단강도 및 옵셋 관점에서 설계 기준에 부합하며 안전계수와 신뢰성 지표 관점에서 보수성이 완화되었다고 판단된다.
Acknowledgements
본 연구는 산업통상자원부 산업핵심기술개발사업(과제번호 : 10063405, 과제명 : 위치유지와 계류 시스템을 적용하여 ARC7 조건에서 연중운용이 가능한 북극해 기반 부유식 해양구조물 형상 개발)의 지원을 받아 수행되었습니다.