Benjamin, TB. (1968). Gravity Currents and Related Phenomena.
Journal of Fluid Mechanics,
31(2), 209-248.

Blumberg, AF. (1977). Numerical Model of Estuarine Circulation.
Journal of Hydraulics Division,
103, 295-310.

Cantero, M., Balachandar, S., García, M., & Ferry, J. (2006). Direct Numerical Simulations of Planar and Cylindrical Density Currents.
Journal of Applied Mechanics,
73(6), 923-930.

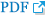
De Cesare, D., Boillat, J-L., & Schleiss, AJ. (2006). Circulation in Stratified Lakes due to Flood-Induced Turbidity Currents.
Journal of Environmental Engineering,
132(11), 1508-1517.

Farhanieh, B., Firoozabadi, B., & Rad, M. (2001). The Propagation of Turbulent Density Currents on Sloping Beds. Scientia Iranica, 8(2), 130-137.
Firoozabadi, B., Afshin, H., & Aram, E. (2009). Three-Dimensional Modeling of Density Current in a Straight Channel.
Journal of Hydraulic Engineering,
135(5), 393-402.

Georgoulas, AN., Angelidis, PB., Panagiotidis, TG., & Kotsovinos, NE. (2010). 3D Numerical Modelling of Turbidity Currents.
Environmental Fluid Mechanics,
10(6), 603-635.

Gill, AE. (1982). Atmosphere-Ocean Dynamics. New York. Academic Press.
Gray, TE., Alexander, J., & Leeder, MR. (2006). Longitudinal Flow Evolution and Turbulence Structure of Dynamically Similar, Sustained, Saline Density and Turbidity Currents..
Journal of Geophysical Research: Oceans Banner, 111.

Hormozi, S., Firoozabadi, B., & Ghasvari, H. (2008). Characteristic Variables and Entrainment in 3-D Density Currents. Scientia Iranica, 15(5), 575-583.
Huppert, HE., & Simpson, JE. (1980). The Slumping of Gravity Currents.
Journal of Fluid Mechanics,
99(4), 785-799.

Lal, PBB., & Rajaratham, N. (1977). Experimental Study of Bluff Buoyant Turbulent Surface Jets.
Journal of Hydraulic Research,
15(3), 261-275.

Lesser, GR., Roelvink, JA., van Kester, JATM., & Stelling, GS. (2004). Development and Validation of a Three-Dimensional Morphological Model.
Coastal Engineering,
51(8–9), 883-915.

Marmoush, YR., Smith, AA., & Hamblin, PF. (1984). Pilot Experiments on Thermal Bar in Lock Exchange Flow.
Journal of Energy Engineering,
110(3), 215-227.

Mueller, C., & Carbone, R. (1987). Dynamics of a Thunderstorm Outflow.
Journal of the Atmospheric sciences,
44(15), 1879-1898.

Natale, MD., & Vicinanza, D. (2001). An Experimental Study of Heated Surface Jet in a Wave Environment. The International Society of Offshore Polar Engineers, 11, 396-403.
Pacanowski, RC., & Philander, SGH. (1981). Parameterization of Vertical Mixing in Numerical Models of Tropical Oceans.
Journal of Physical Oceanography,
11, 1443-1451.

Paik, J., Eghbalzadeh, A., & Sotiropoulos, F. (2009). Three-Dimensional Unsteady RANS Modeling of Discontinuous Gravity Currents in Rectangular Domains.
Journal of Hydraulic Engineering,
135(6), 505-521.

Patterson, MD., Simpson, JE., Dalziel, SB., & Nikiforakis, N. (2005). Numerical Modelling of Two-Dimensional and Axisymmetric Gravity Currents.
International Journal for Numerical Methods in Fluids,
47, 1221-1227.

Raffel, M., Willert, CE., & Kompenhans, J. (1998). Particle Image Velocimetry: a Practical Guide. Springer Verlag: Berlin. p 253.
Raffel, M., Willert, CE., Wereley, ST., & Kompenhans, J. (2007). Particle Image Velocimetry. Springer Verlag: Berlin. p 448.
Sato, T., Tonoki, K., Yoshikawa, T., & Tsuchiya, Y. (2006). Numerical and Hydraulic Simulations of the Effect of Density Current Generator in a Semi-Enclosed Tidal Bay.
Coastal Engineering,
53(1), 49-64.

Shanack, S. (1960). A Theoretical Current Density Ansatz for the Quiet Day Solar Semi-Diurnal Tidal Mode of Oscillation of the Ionosphere.
Journal of Atmospheric and Terrestrial Physics,
17(4), 337-343.

Simpson, JE. (1969). A Comparison between Laboratory and Atmospheric Density Currents.
Quarterly Journal of The Royal Meteorological Society,
95(406), 758-765.

Thomas, LP., Marino, BM., & Linden, PF. (1998). Gravity Currents over Porous Substrates.
Journal of Fluid Mechanics,
366, 239-258.

Thomas, LP., Marino, MB., & Linden, PF. (2004). Lock-Release Inertial Gravity Currents over a Thick Porous Layer.
Journal of Fluid Mechanics,
503, 299-319.

Wakimoto, RM. (1982). The Life Cycle of Thunderstorm Gust Fronts as Viewed with Doppler Radar and Rawinsonde Data.
Monthly Weather Review,
110, 1060-1082.

White, BL., & Helfrich, KR. (2008). Gravity Currents and Internal Waves in a Stratified Fluid.
Journal of Fluid Mechanics,
616, 327-356.

 ) are results for the initial salinity of 20 psu (CASE2); and the red diamonds (
) are results for the initial salinity of 20 psu (CASE2); and the red diamonds ( ) are results for the initial salinity of 30 psu (CASE3).
) are results for the initial salinity of 30 psu (CASE3).