|
 |
- Search
| J. Ocean Eng. Technol. > Volume 32(5); 2018 > Article |
|
Abstract
The construction of large scale harbor structures at Maengbang beach, which is located on the eastern coast of Korea, is of great concern because it may cause disastrous beach erosion in the vicinity. Therefore, a hydraulic model experiment was conducted to examine the morphological changes after such construction. The water depth was scaled using the method of Van Rijn (2010), which is a well-known scale law, but the results appeared to be overestimated. The present study developed a new scale law that applies an equilibrium beach profile formula to scale the model evolution to the prototype scale. When compared with survey data observed at Maengbang beach, the proposed method showed better agreement than the method of Van Rijn (2010).
최근 항만 외곽방파제의 확장 및 신설 등 해안구조물이 지속적으로 건설됨에 따라 인근 해안 환경의 변화가 초래되고 이로 인하여 사질 해변에서는 해안 침식이 심각하게 발생하고 있다. 공사 전 이러한 육역 개발로 인한 환경영향평가가 해안 침식 측면에서도 검토가 철저히 이루어져야 하지만 현재 그렇지 못한 실정이다. 항만 시설이 축조된 후 해안침식 피해가 해안침식 피해가 심각하게 발생한 후 이를 저감하기 위한 목적으로 다양한 해안 구조물이 추가로 건설되고 있다. 그러나, 이 또한 항만시설과는 다르게 마땅한 설계 기준이 없는 관계로 시행착오에 의존하는 무분별한 설계가 이루어지고 있는 실정이다. 이렇게 건설된 해안구조물은 파랑장 및 바람장 등의 해역환경변화를 또다시 유발시킴으로써, 해안구조물로 인한 2차 침식 피해가 발생하는 지역이 지속적으로 증가하는 추세이다. 이러한 기술적 한계에서 새로운 항만 및 해안구조물의 축조로 인한 해안 환경의 변화를 면밀히 파악하고 침식 피해를 줄이기 위하여 기술적 방법을 찾는데 있어 수리실험의 수행은 절실하다. 그러나 국내 수리실험 연구로는 구조물 안정성 검토에 대한 실험 목적이 대부분인 수리모형실험이 수행되었고(Lee and Yoon., 2006; Lee et al., 2008; Oh et al., 2011; Cho et al., 2002; Kwak et, al., 2003), 3차원적인 수리모형실험(Hur, 2004; Lee et al., 2009)이 이루어졌다. 그러나 해안구조물 주변의 3차원적인 흐름 특성을 파악하기에는 아직 미진한 실정이며 지형 변화를 파악하기에도 부족한 시간과 모래 투입량으로 이동상 수리실험이라고 간주하기에 부족한 실험이 많았다. 이와 같이 국내 수리모형실험은 대부분 구조물 안정성에 대한 검토를 중심으로 연구가 수행되었고 이동상 수리모형실험을 통한 연구는 아직 국내 여건상 선진국에 비하여 턱없이 부족한 실정이다.
국외에서는 파랑장이 지배하는 해안에서의 모래 이동을 연구하기 위하여 오래전부터 다양한 축척 연구가 이루어졌으며 Table 1은 그 동안 해빈단면 실험을 목적으로 제시된 국외의 다양한 이동상 수리모형실험의 축척율 중 대표적인 것을 보여주고 있다.
본 연구에서는 이러한 다양한 축척법의 유도과정과 쇄파대에서의 해저면 변화에 대한 수리실험에의 적용성을 검토하였고 축척된 수리모형에서의 실험 결과가 아직 현장 지형을 잘 재현하지 못하고 있다고 판단하였다. 따라서 범용적으로 쓰이는 평형해빈단면 경험식을 이용하여 새로운 축척법을 고안하였고 맹방해변에 대한 이동상 3차원 수리모형실험 관측 결과에 적용하여 제안된 축척법이 상당히 만족할 만한 결과를 제공하고 있다고 판단하였다.
맹방해변의 해빈단면 조사자료를 분석한 결과 해변 내 평균 경사는 약 1:30~1:40 사이의 경사를 나타내고 있으며, 해변 내 17개의 기준점에서 해저질 입경을 분석한 결과 해저질의 중앙입경 D50은 0.697mm로 분석되었다. 해빈 축척 계수(Profile scale factor) A는 맹방해변 관측 자료의 평균 해빈 경사가 1:30~1:40 정도로서 해빈 축척 계수 A는 Table 2에 제시된 바와 같이 A=0.185m1/3으로 추정된다. 해빈 단면 축척계수를 이용한 평형해빈단면식(Equilibrium beach profile equation), h=Ay2/3과 현지의 해빈 단면자료를 비교하여 파랑의 변형이 이루어지는 천이영역으로부터 천해까지의 수심에서 유사한 해빈 경사를 보여주고 있다. 맹방 해변의 해안선은 Fig. 4에서 도시된 바와 같이 반경 46.1km의 원주상에 38N°의 주파향으로 설정하였다. 이러한 실지형의 해안선 곡률 조건을 직선 형태 조파계로 이동상 실험을 진행하는 경우 이로 인한 곡률로 중앙으로의 연안표사가 발생할 수 있으므로 조파기와 마찬가지로 해안선 및 지형을 직선적 좌표계로 환원하여 수리실험을 수행하였다.
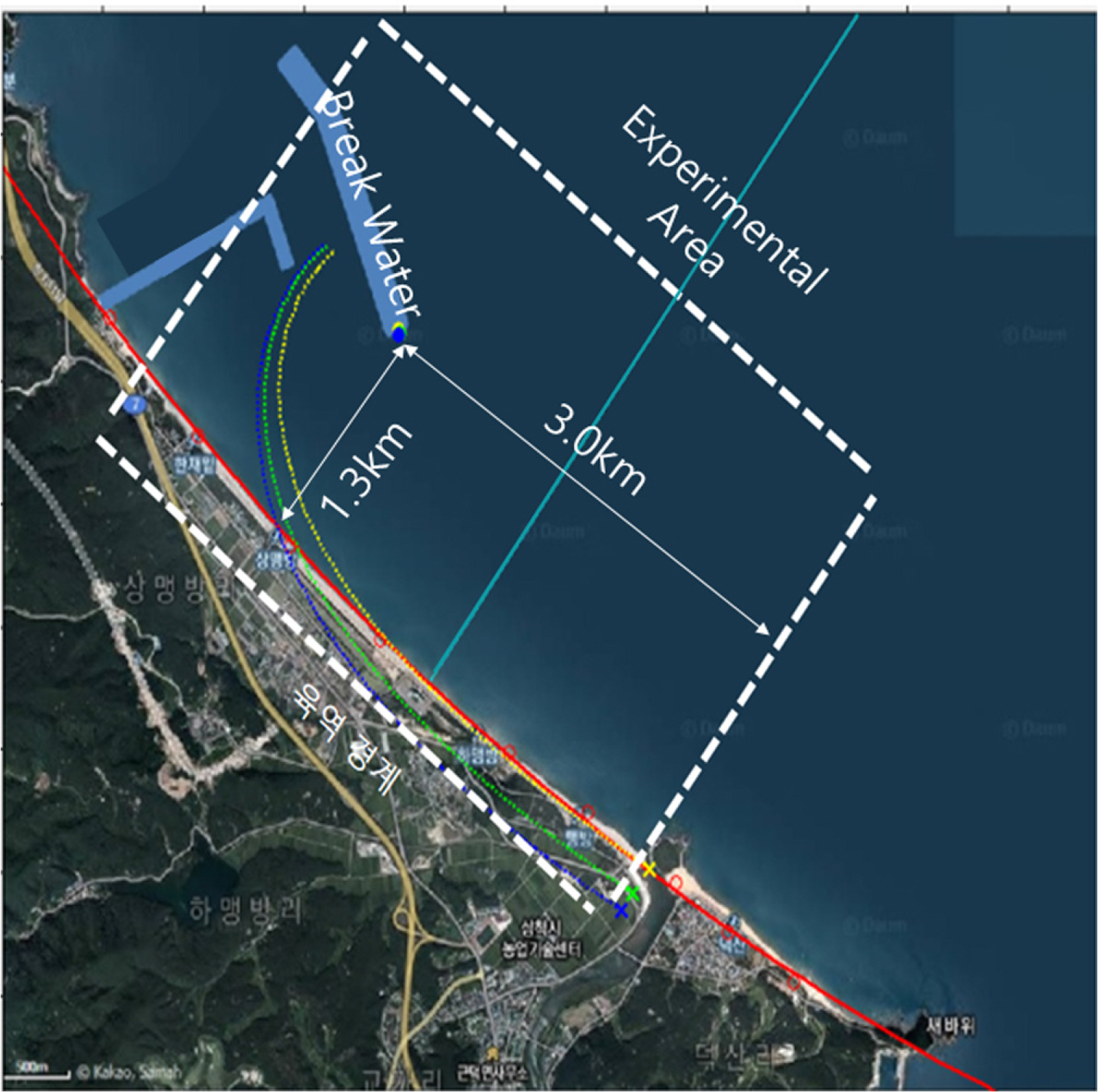
중국 천진에 위치한 Tianjin Research Institute for Water Transport Engineering(TIWTE) 3차원 수조 실험실에서 4km 길이의 맹방 해변을 수평 축척 1:90으로 수리모형실험을 진행하였다. 수조의 양쪽 측면구간은 파랑의 회절이나 소산을 최소화 할 수 있는 여분의 공간을 확보하여 실험을 진행하였다. 아래 제시한 Fig. 5는 맹방해변 위성사진에 평면수리모형실험 영역을 표기하여 도시하였다. 해안선과 평행한 방향으로 50m의 조파기 길이를 확보하였고, 육상으로부터 35m의 외해 이격 공간을 확보하여 수리실험을 진행하였다. Fig. 5의 노란 파선은 상류 해안의 해안선이 유지되기 위하여 필요한 평형해안선으로 노란 파선을 따라 매립과 병행한 인공 해빈을 조성하지 않으면 상당한 모래가 회절파 유역으로 유입하게 된다. 따라서 상류 해안이 침식되었다고 가정하여 얻은 또 다른 평형해안선인 파란 파선처럼 상류 해안의 대규모 침식이 우려되는 상황이 초래될 수 있음을 보여준다.
이동상 실험에서 연안표사 오류를 최소화하기 위하여 맹방해안선이 반경 46.1km의 원주상에 38N°의 주파향으로 설정하여 놓인 점을 감안하여 Fig. 6과 같이 극좌표를 펼친 직교좌표에서 평면수리모형실험이 수행되도록 하였다. 이는 원래의 해안 지형을 반영하여 오목한 원주 상의 해안선을 형성하게 되면 이동상 실험에서 조파기와 직선으로 놓이는 수리실험 조건상 중앙으로 연안표사가 발생하여 중앙에서 퇴적 현상이 발생하고 경계 양측에서 침식되는 표사이동 실험상 오류를 최소화하였다.
평면수리모형실험의 북측 경계는 이안제 형태의 외곽방파제이지만 이안제 배후에서 파향이 교차하고 배후에 제작장이 놓인 위치에서 흐름이 없는 것으로 간주하였다. 남측 경계는 덕봉산 바로 북측에 위치한 마읍천 하구로 설정하였다.
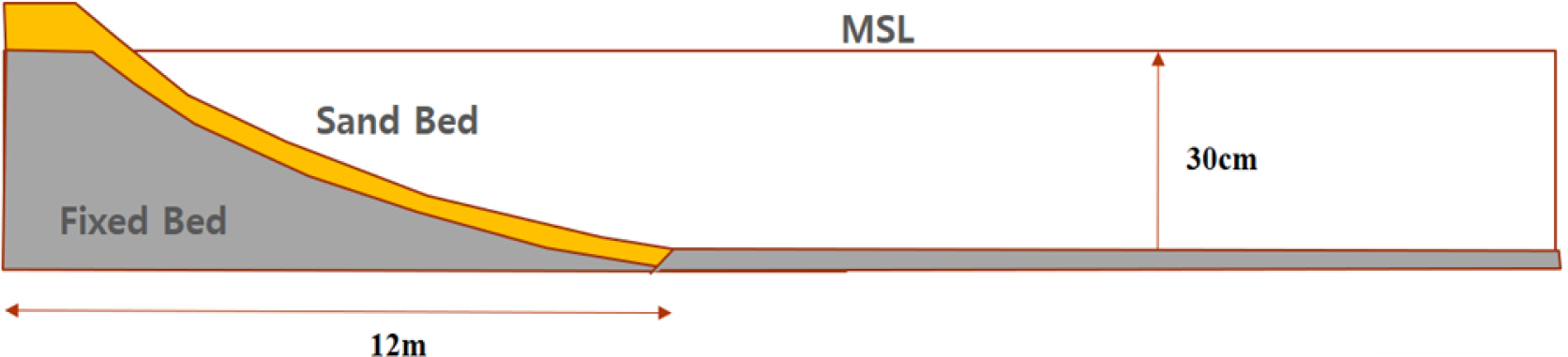
본 연구에서는 평균수면의 높이는 30cm로 유지하였다. 실험사는 Fig. 7과 같이 모르타르 고정상 베드를 조성하고 10cm의 모래를 수심 30cm이하, 해빈단면 12m 구간에 고정상 베드에 균일하게 포설 하였다. 따라서 전체 모래로 이루어지는 이동상 실험의 체적은 50m×12m×0.1m = 60m3에 달하였으며, 30cm를 넘는 구간은 동일 수심으로 고정상 베드를 조성하였다. 실험사를 균일하게 포설하였으나 모래로 이루어진 저면이 거의 직선적인 해안선과 등수심선이 형성될 수 있도록 모래의 공극율을 맞추고 조파기의 균일성을 확인하는 과정을 수행하였다(Fig. 8).
사용되는 이동상 모래의 비중은 2.6이며 현재 가장 최소한으로 만들 수 있는 입경은 0.1mm(축척 계수: 0.063m1/3에 해당)로서 이 모래를 사용하되 평균 입경이 0.125mm를 넘지 않도록 하였다. 이동상 실험은 사용하는 모래 입경에 따라 현지 지형에 맞는 해빈 경사를 초기에 조성하지 않으면 파도의 작용 하에서 입경에 따라 형성되는 평형해빈단면(Equilibrium beach profile)이 달라지기 때문에 횡단표사 조건 충족을 위한 평형해빈단면식의 검토를 수행하였으며, 평형해빈단면 조건 불충족 시 평형해빈 단면을 충족하기 위한 수리모형실험이 추가로 수행되어야 함으로써 실험사에 대한 평형해빈단면이 초기 이동상 해저면 조건으로 조성되었다.
이동상 수리모형실험에서 수평과 수직 축척율은 Van Rijin(2009) 연구 결과를 기초로 하여 분석하였다. 수평 축척과 수직 축척의 관계와 해안선 또는 해저 지형의 변화시간의 축척은 식 (1)과 식 (2)에 제시하였다.
여기서 nl은 수평방향 축척율이며 nh는 수직 방향 축척율, nTm은 Morphology 변화 시간 축척, nd50는 중앙입경의 비율 ns-1은 상대비중 s-1의 비율이다.
대상 해안인 맹방 해변의 모래입경은 17개 기준점에서 관측한 평균 입경은 0.697mm이다. 따라서 이동상 실험에서 사용하는 모래의 입경이 0.1mm이므로 nd50=6.7이 된다. 따라서 모래의 비중이 같은 경우에 수평과 수직 축척의 왜곡이 없는 nl/nh=1인 경우는 식 (1)부터 다음 결과를 도출하였다.
따라서 수직은 물론 수평도 약 1:30의 축척을 주어야 하지만 4km가 넘는 해안을 수평 축척으로 달성하기는 어려우므로 수평과 수직의 왜곡을 허용하여 수리모형실험을 수행하였다. 수평을 1:90으로 계획하는 경우 식 (1)을 다시 적용하면 수직 축척은 1:70.7이 된다. 그러나 편의상 수평 축척을 1:70으로 수행하였다.
식 (2)를 이용하여 해안선 변화 축척율을 구하면 아래와 같다.
따라서 지형의 수평 및 수직 축척이 이루어지고 대상 해역의 평균 파고의 10배 큰 이상 파고를 적용하였을 때, 연안 표사량은 약 100배 증가 효과를 발휘한다고 가정하고, nTm=10.80과 30시간을 곱하면 약 3.4년 후의 해안선 변화 효과를 얻을 수 있다. 파랑 주기 축척과 관련된 시간 축척율 nT를 구하는 방법은 여러 가지 방법이 가능하나 모래의 이동이 우월한 천해 수심에서 위상 속도를 유지 시켜 굴절과 회절, 천수 효과가 유지되도록 식 (6)과 같이 유도하였다.
해안선 및 등수심선 등의 평형을 확인하기 위한 실험은 지속시간이 길어 그 변형 과정은 평상파에 의하여 지배적으로 진행되기 때문에 평상파 조건에서 수행하는 것이 바람직하다. 그러나 일반적으로 해안선 및 등수심선 등의 평형 유지를 위하여 5년, 10년 및 50년 이상의 시간이 필요할 수 있다. 이를 수리실험으로 재현하려면 파랑 조건의 평형만을 충족시키면 되는 항만 수리실험과는 다르게 원칙적으로 수직 축척에 0.56승을 취한 것만큼의 이동상 실험이 필요하다. 따라서 수평 축척 1:200의 축척에서 표사 이동이 평형에 도달하는 데 필요한 시간이 10년이라고 가정하면 0.1mm의 실험사에 대하여 7~8개월이 넘게 조파기를 작동시켜야 한다는 계산 결과가 나온다. 그러나 이러한 실험은 거의 불가능한 상황이므로 연안표사 이동환경을 촉진시키기 위한 방법을 수용할 수밖에 없는 것이 평형해안선을 조사하는 이동상 실험의 근본적 한계이다. 해안선 변화에 적용되는 연안표사량 산정식은 Energy flux의 함수로 제시되며 근사적 계산법으로 파고의 제곱에 비례하는 것으로 보고 있다. 따라서 파고를 10배 증가시키면 100배의 연안표사 가속 효과가 발생할 수 있다고 판단되며 7~8개월가량 걸리는 이동상 실험이 48~72시간 수행하면 가능할 수도 있다는 계산이 나온다. 그러나 평상파 조건과 비교하여 이상파 조건에서의 쇄파대가 크게 확대된다는 점을 염두에 두고 무리한 지속시간 축척이 이루어지지 않게 실험을 계획할 필요가 있다.
본 실험의 경우 해당 지역의 연평균 파고인 0.5m에 비해 7.25배 큰 3.63m, 즉, 1:70의 수직 축척에서의 조파 조건으로는 5.18cm가 적용되고 있다. 그리고 명확한 학술적 분석을 위하여 규칙파 실험이 계획되었다.
이동상 수리모형 실험의 축척율은 일반적으로 실지형(Prototype)과 수리모형(Laboratory)의 계수 비율로서 n=pp/pm으로 표현되며 여기서 pp는 실 지형 자연계수이고 pm은 수리모형 실험계수이다. 대부분 수리모형의 계수가 실 지형의 계수보다 훨씬 작게 설계되므로 n>1의 값을 갖는다. Table 3에는 실험의 목적에 따라 선택되는 대표적인 축척법이 제시되었다. 3가지 고정상 수공학적인 축척법과 2가지의 이동상의 지형학적인 축척법이 제시되었다.
최근 Van Rijin(2010)의 이동상 실험에서의 수평 및 수직 축척율에 대한 식을 제안하였다. 수평 축척과 수직 축척의 관계와 해저 지형의 변화시간에 대한 축척은 아래 식에 제시하였다.
여기서 nl은 수평방향 축척율이며 nh는 수직 방향 축척율, nTm은 지형 변동 시간 축척, nd50는 중앙입경의 비율 ns-1은 상대비중인 s-1의 비율이다.
해안축척모형의 경우, 가장 널리 받아들여지는 요구 사항은 실 지형과 수리모형의 해빈단면 특히, 쇄파대에서의 평형해빈 단면 간의 유사성을 취득하는 것이다(Hughes and Fowler, 1990). 따라서 수리모형실험과 실 지형 조건의 평형해빈단면이 지배하는 해빈 특성을 동일하게 맞추어야 한다. 본 논문에서는 이러한 해빈 특성을 가장 잘 대변하는 축척율 산정관계식을 평형해빈 단면 공식으로부터 직접 유도하였다.
해빈단면은 복잡한 현상에 의하여 형성되어 단순한 함수로 표현되는데 한계가 있지만 평형을 이루는 해빈단면은 외해로 나갈수록 수심이 깊어지는 곡선식으로 표현되어왔다. 즉, 그 곡선식은 주로 관측치와 비교하여 하나 또는 두 개 정도의 변수를 설정하는 식으로 제시된다. 대표적인 평형해빈단면 곡선식은 평형에 도달하였을 때 적용되는 식이지만 목표단면(Target profile)이라는 수단으로서 식 (9)과 같이 축척 계수(Scale factor)라는 하나의 계수로 표현되는 식이 널리 쓰인다. 이 식은 경험식으로 간주 될 수 있지만 쇄파대 내에서 일정 Volumetric wave dissipation이라는 가정하에서 Dean(1977)에 의하여 유도되었으며, Wang and Kraus(2005)에 의해 규칙파는 물론 불규칙파에도 성립한다는 것을 대형수조(Supertank) 수리모형 실험을 통해 입증하였다.
여기서 축척 계수 A는 모래 입자의 특성, 입사파의 특성에 따라 달라질 수 있으나 일반적으로 침강 속도 또는 입경에 대한 정보로 구성되었다고 간주한다. 평형해빈단면은 횡단표사로 인한 해빈단면 변화를 예측하는 공학적 수단인 Sbeach 모형에서와 같이 목표해빈단면으로 채택되는 등 많은 부분에서 널리 이용되고 있다(Dean, 1991; Miller and Dean, 2004). 그리고 최근 Kim and Lee, (2018)은 평형해빈단면식을 이용하여 파랑에너지의 유입에 따라 해안선이 어떻게 반응하는지 예측하는 수단으로 사용하였다.
본 연구에서는 이러한 해빈 단면 특성을 이용하여 이동상 표사 이동이 가장 활발한 영역에서 해빈단면 형상의 축척이 제대로 반영되도록 새로운 방법을 제시하였다. 식 (9)에 축척을 적용하면, 여기서 nA는 축척계수의 비율이다.
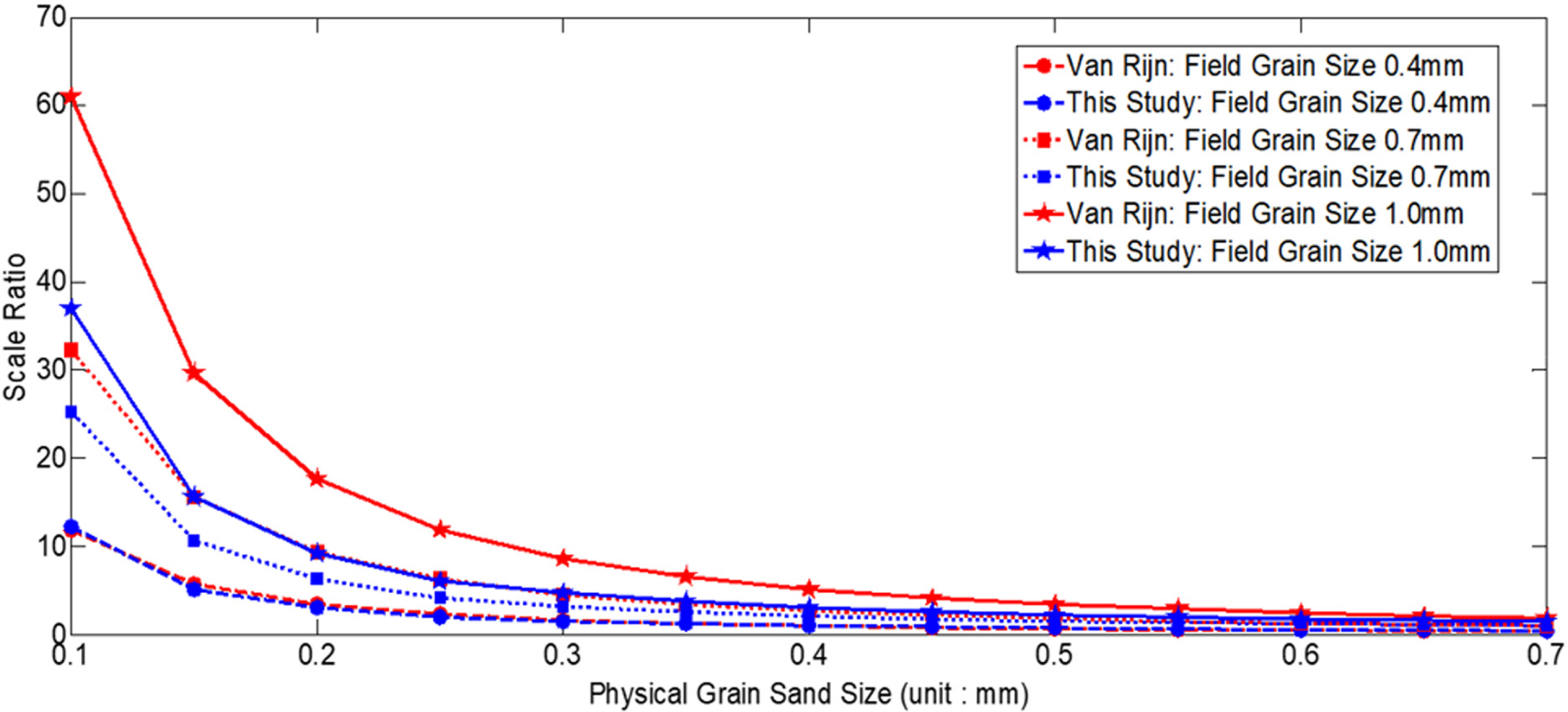
Fig. 9(a)는 실 지형(Prototype)의 표사 중앙입경이 D50=0.4mm라고 가정하고, 실험사 중앙입경(D50=0.1mm)을 적용한 평형해빈 단면 식을 보여준다. Fig. 9(b)는 식 (10)에 의하여 비왜곡되는 축척율인 12.19을 수평 및 수직 좌표에 적용한 경우 해빈 단면이 정확히 일치하는 것을 보여주고 있다. Fig. 10(a)는 실험사 중앙입경(D50=0.1mm)에 대하여 수직 축척은 그대로 두고(비왜곡 축척: 1:12.19) 수평 축척을 1:20으로 하였을 때의 평형해빈단면 식을 보여준다. 비왜곡인 경우 식 (10)에 의하여 수직 축척율이 얻어지는데 15.45를 적용하였을 경우 비왜곡임에도 해빈단면이 Prototype과 잘 일치하는 것을 보여주고 있다.
이동상 실험에서의 수평 및 수직 축척율은 Van Rijin(2009)의 보고서 내용을 토대로 분석하였다. 대상 해안인 맹방 해변의 모래입경은 17개 기준점에서 관측한 평균 입경은 0.697mm이다. 따라서 이동상 실험에서 사용하는 모래의 입경이 0.1mm이므로 nd50=6.97이 된다. 따라서 모래의 비중이 같은 경우에 수평과 수직 축척의 왜곡이 없는 nl/nh=1인 경우는 식 (11)로부터 다음 결과를 얻는다.
따라서 수직은 물론 수평도 약 1:32의 축척을 주어야 하지만 4km가 넘는 해안을 수평 축척으로 달성하기는 어려우므로 수평과 수직의 왜곡을 허용하였다. 수평을 1:90으로 계획하는 경우 식 (7)을 다시 적용하면 수직 축척은 1:71.3이 된다.
대상 해안인 맹방 해변의 모래 중앙입경은 0.697mm이고 실험사의 모래 중앙입경은 0.1mm이므로 nA=2.93이 된다. 따라서 모래의 비중이 같은 경우 수평과 수직 축척의 왜곡이 없는 nl/nh=1인 경우는 식 (12)으로부터 다음 결과를 얻는다.
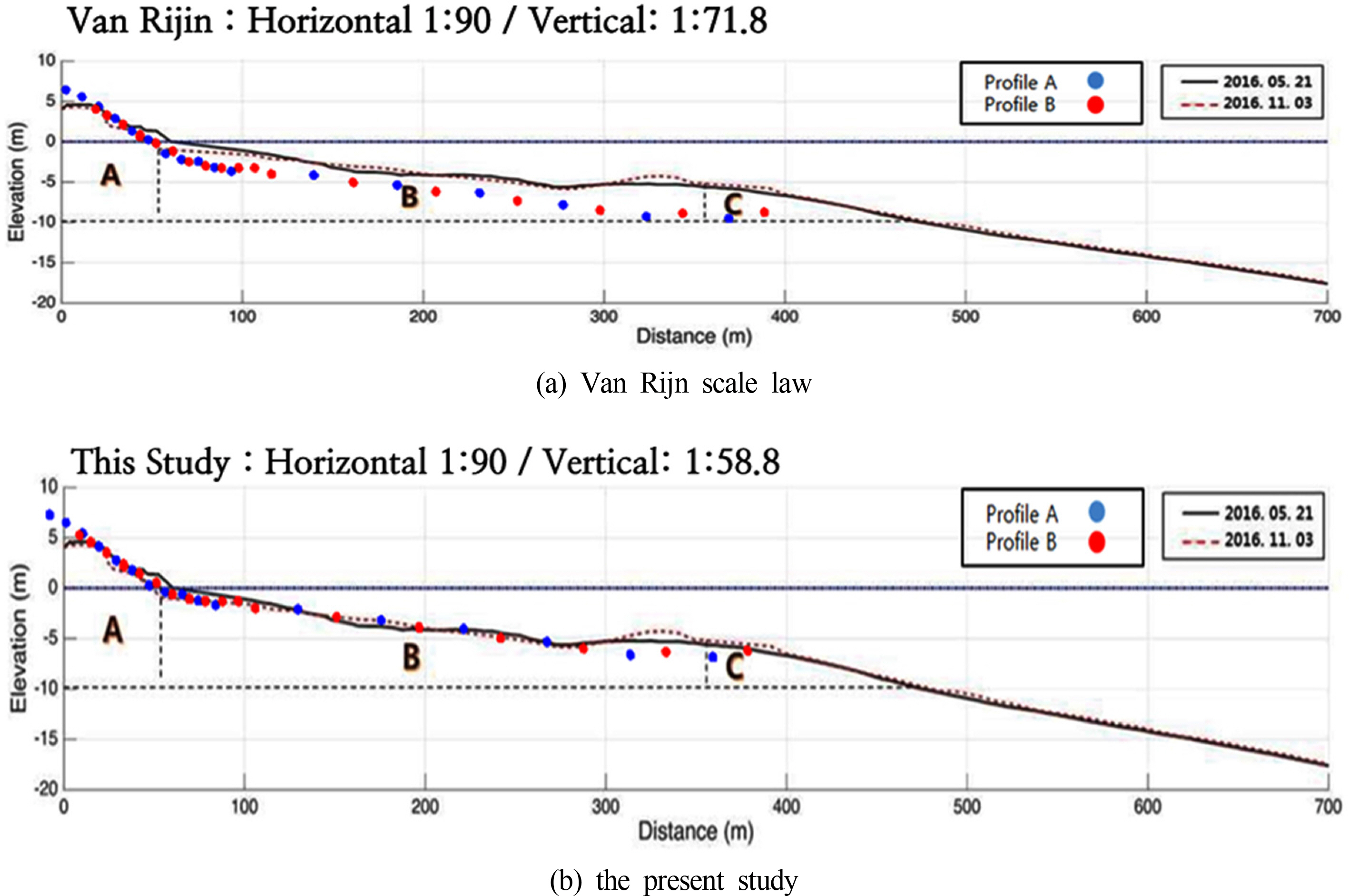
따라서 수직은 물론 수평도 약 1:25의 축척을 주어야 하므로 Van Rijn 결과처럼 4km가 넘는 해안을 수평 축척으로 달성하기는 어려우므로 수평과 수직의 왜곡을 허용하였다. 수평을 1:90으로 계획하는 경우 식 (10)를 다시 적용하면 수직 축척은 Van Rijn 축척법에 의한 결과보다 작은 1:58.8이 된다.
Van Rijn 및 평형해빈단면 축척법을 이용하여 실측 해빈단면 기준선 2개소 기준선(Profile A and B)과 평형해빈단면과의 비교를 수행하였다(Fig. 12). 비교 결과 평형해빈단면의 축척법이 Prototype의 해빈단면 실측 조사자료와 비교적 일치하고 있는 것으로 분석되었다.
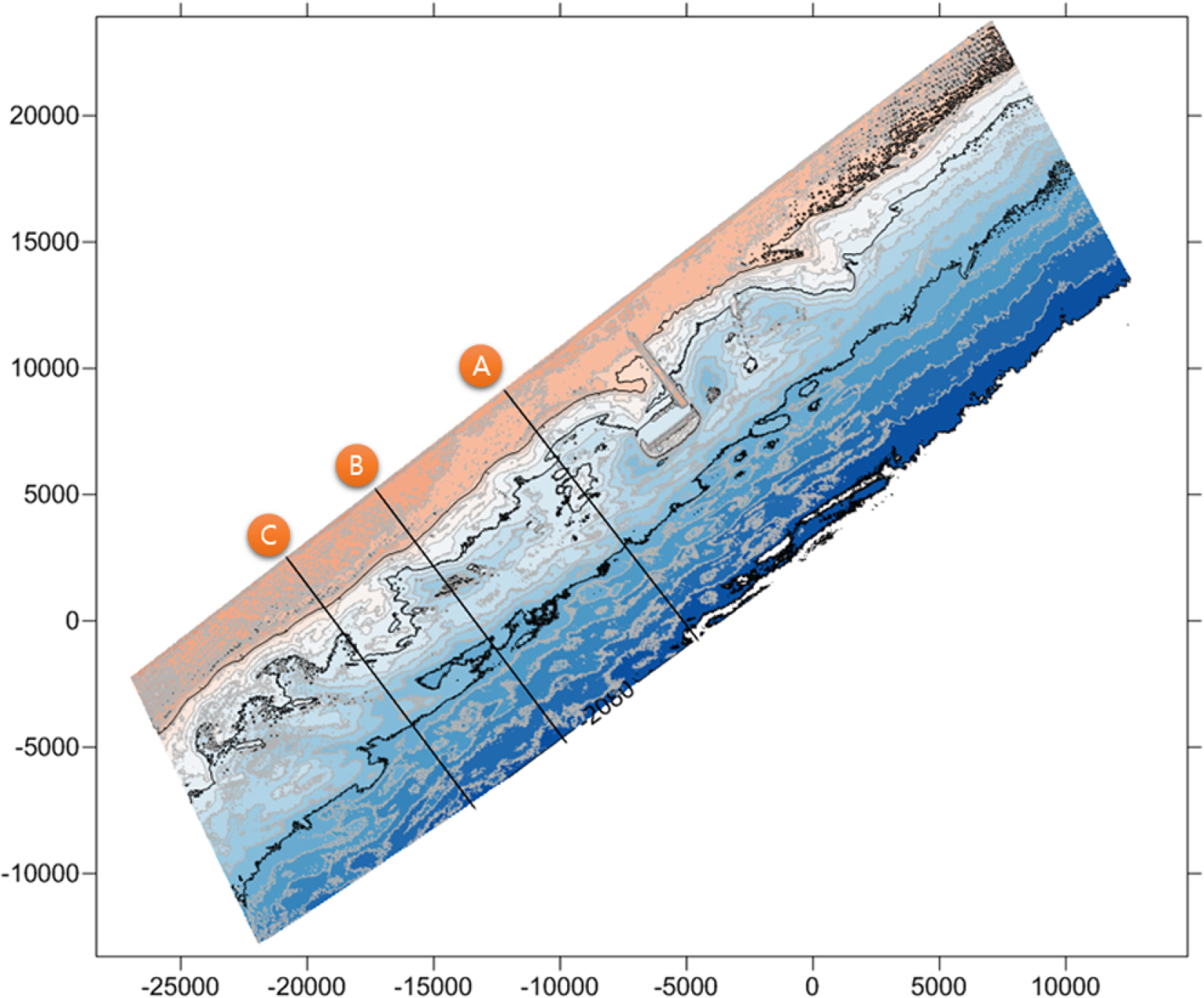
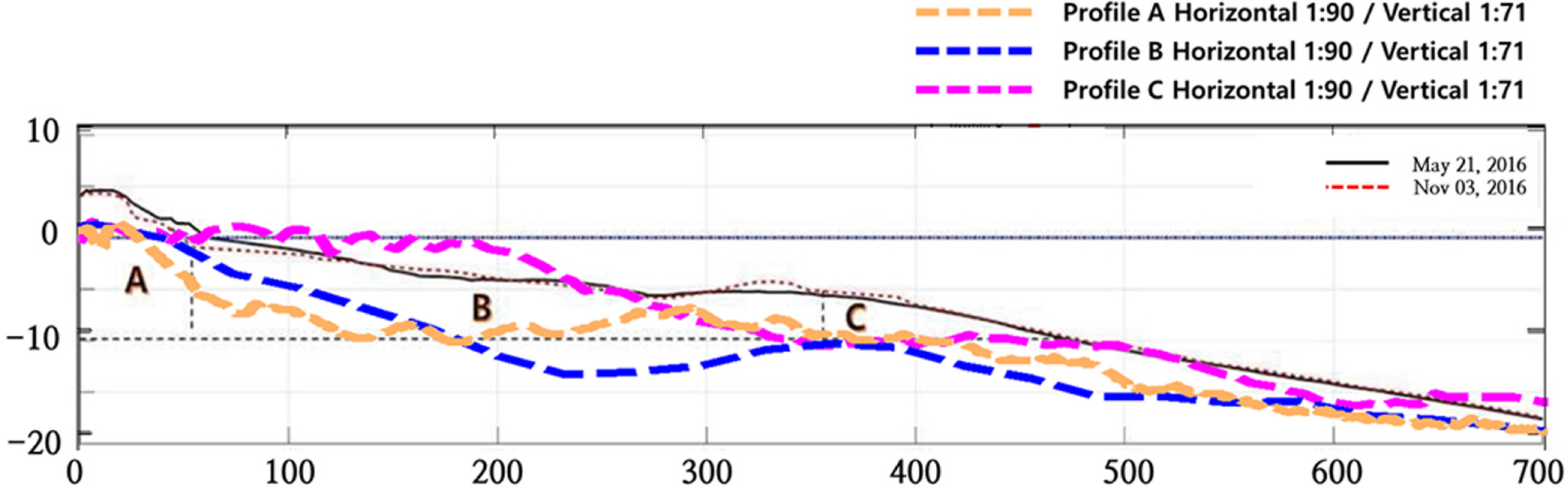
실험 후 분석을 수행하기 위하여 Trimble사의 TX-8 레이저 스캐너를 이용하여 지형 스캔 결과를 Fig. 14에 제시하였고, 스캔자료를 이용하여 수심도를 Fig. 13과 같은 기준선 A, B, C를 따라 Fig. 15와 같이 스캔 수심 자료와 대상 해역에서 관측된 해빈 단면자료를 서로 비교하였다. 실 지형 해빈단면 자료는 방사제가 건설되지 않은 조건에서의 대상 해변의 모니터링 관측 해빈단면 자료로서 수리모형실험 자료는 방사제와의 거리에 따라 파랑 변형과 흐름 조성 환경에 따라 실제로 얼마만큼의 정량적 수심 변화를 초래한다.
따라서 어떤 축척법을 적용하는지에 따라 실 지형에서의 수심 변화의 차이는 크게 발생할 수 있으므로 정확한 축척법의 적용 및 선정은 매우 중요하다. Fig. 16에 Van Rijn 축척법의 결과가 제시되었다. 비교적 과도한 수직 축척이 이루어지고 있다고 판단된다. 수리모형실험 당시 모래량이 충분하지 않은 관계로 실 지형의 Berm(수심 + 육역) 높이와는 다르게 거의 해수면 수준에서 파랑에 의한 Dune이 자연적으로 형성되며 Run-up이 제어되었다.
본 연구는 맹방해변의 이안 외곽구조물 설치에 따른 수리모형실험을 수평축척 1:80에 대한 실험을 수행하여 파랑 작용에 의한 이동상 해빈단면 수리모형실험에 적합한 축척법으로 Dean의 평형해빈단면 공식을 이용한 축척법을 제시하였다. Van Rijn (2010)제안법과 비교하여 비왜곡모형(Non-distorted model)은 물론 왜곡의 경우에도 축척율이 작게 산정되었다. 즉, 3차원 수리실험이 수행된 왜곡모형의 경우 현지 해빈단면 자료와 비교하여 Van Rijn 축척법에 의한 것은 과대평가되고 있었으나 본 연구에서 제안된 축척법은 좀 더 만족할 만한 결과를 도출하고 있다고 판단된다.
따라서 제안된 축척법을 적용한다면 수리모형 실험에 의한 해저면 변동 실험 결과로부터 대상 해안에 건설되는 외곽방파제에 의한 해안선 및 해저면 변화 그리고 침식 저감 해안구조물이 배치되는 경우 해안선 및 해저면 변화를 좀 더 정확하게 평가할 수 있을 것으로 기대된다. 그러나 아직 현장 적용 사례가 부족한 관계로 이와 관련된 좀 더 다양한 연구 성과가 도출되기를 기대한다.
후기
본 논문은 2018년 해양수산부 재원으로 해양수산과학기술진흥원(연안침식 관리 및 대응기술 실용화)의 지원 및 강원대학교전임교원 기본 연구비 지원사업(620160115)의 지원 받아 수행된 연구 결과 중 일부임을 밝히며, 연구비 지원에 감사드립니다.
Fig. 6.
Hydraulic model experiment area (50 m × 35 m) and harbor facilities plan of scale 1:90 after polar coordinate transformation
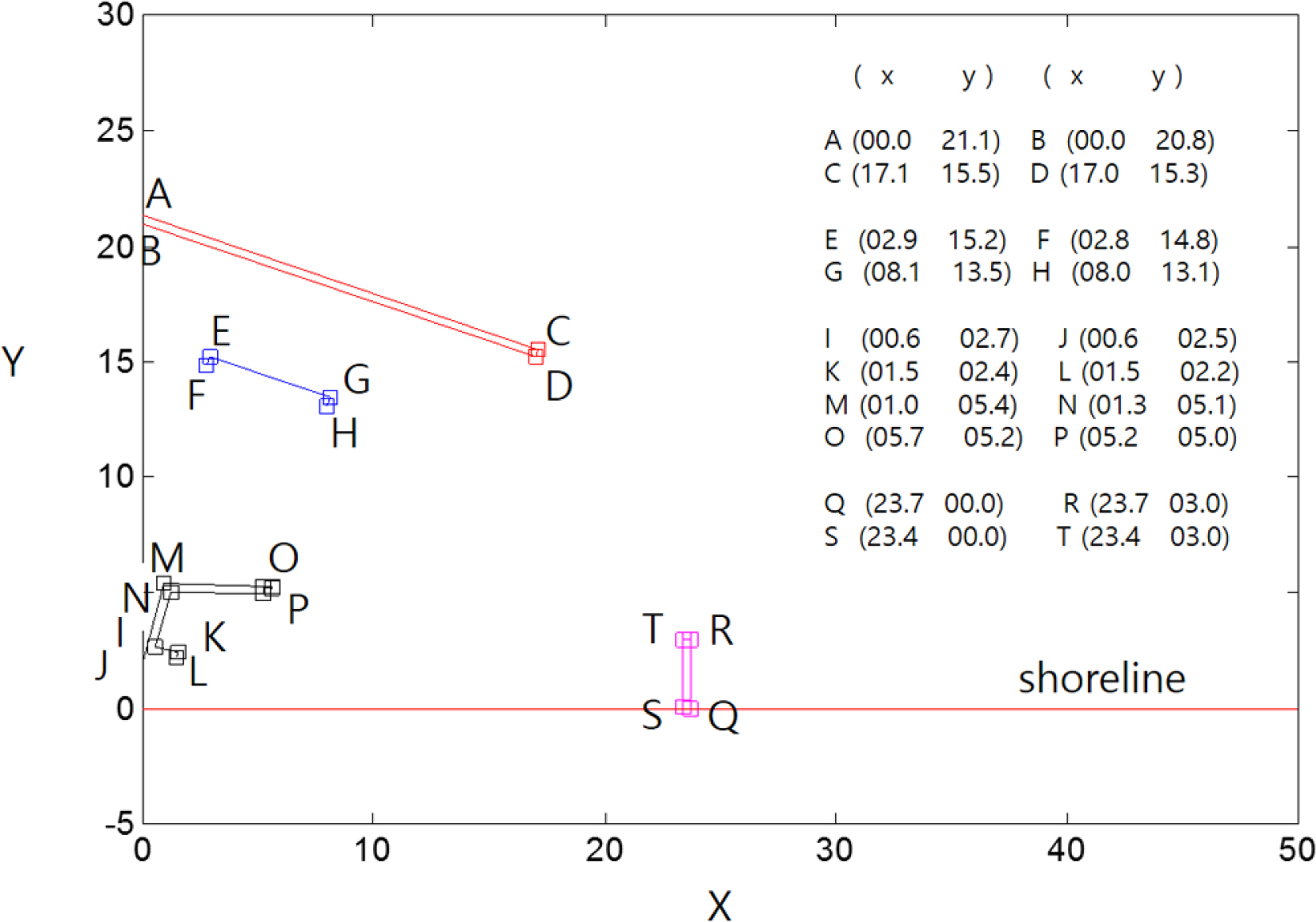
Fig. 9.
(a) Equilibrium beach profiles for prototype and laboratory sand sizes, and (b) non distorted beach profiles after 12.19 times extension of laboratory scale
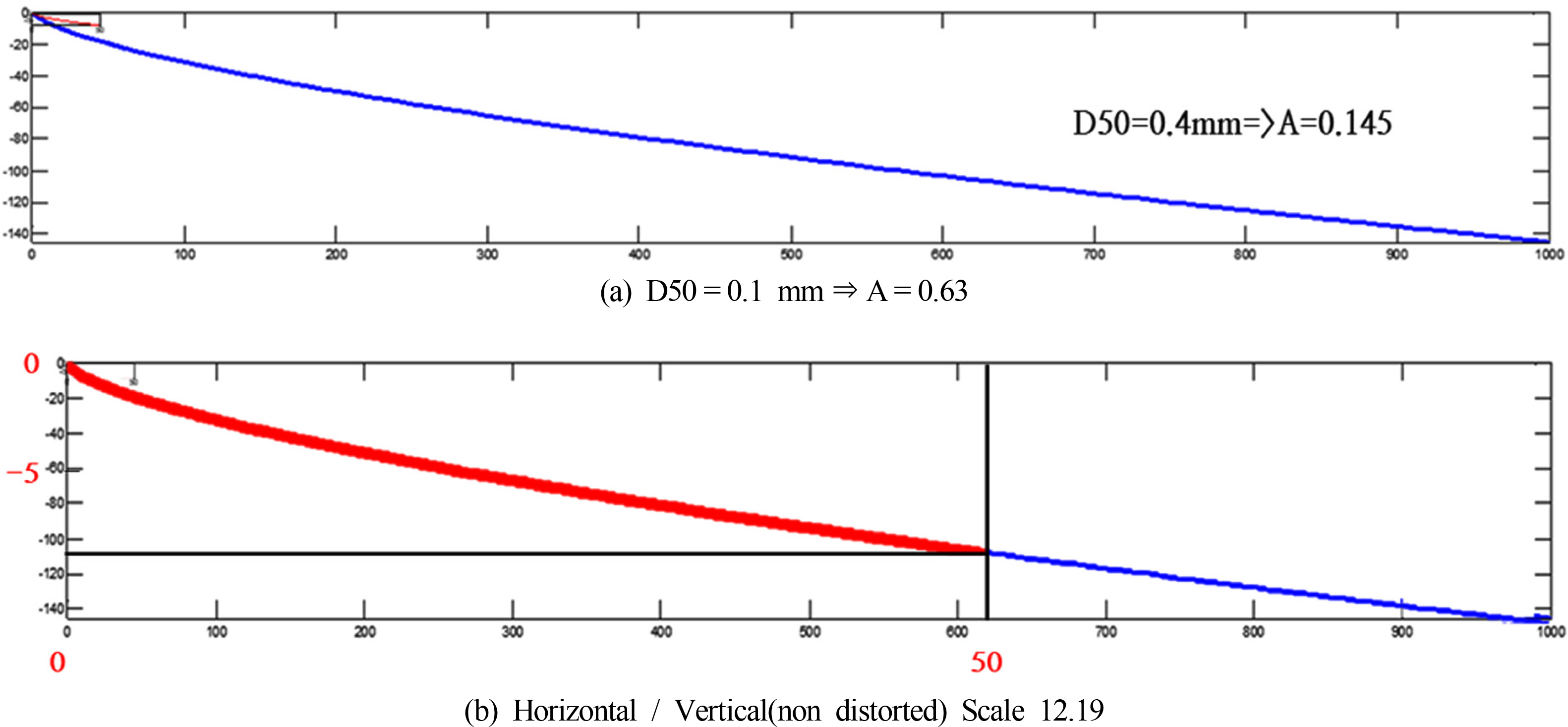
Fig. 10.
(a) Equilibrium beach profiles for more extended horizontal scale 1:20, and (b) distorted beach profiles for vertical scale 1:15.45 obtained from Eq. (10) for horizontal scale 1:20
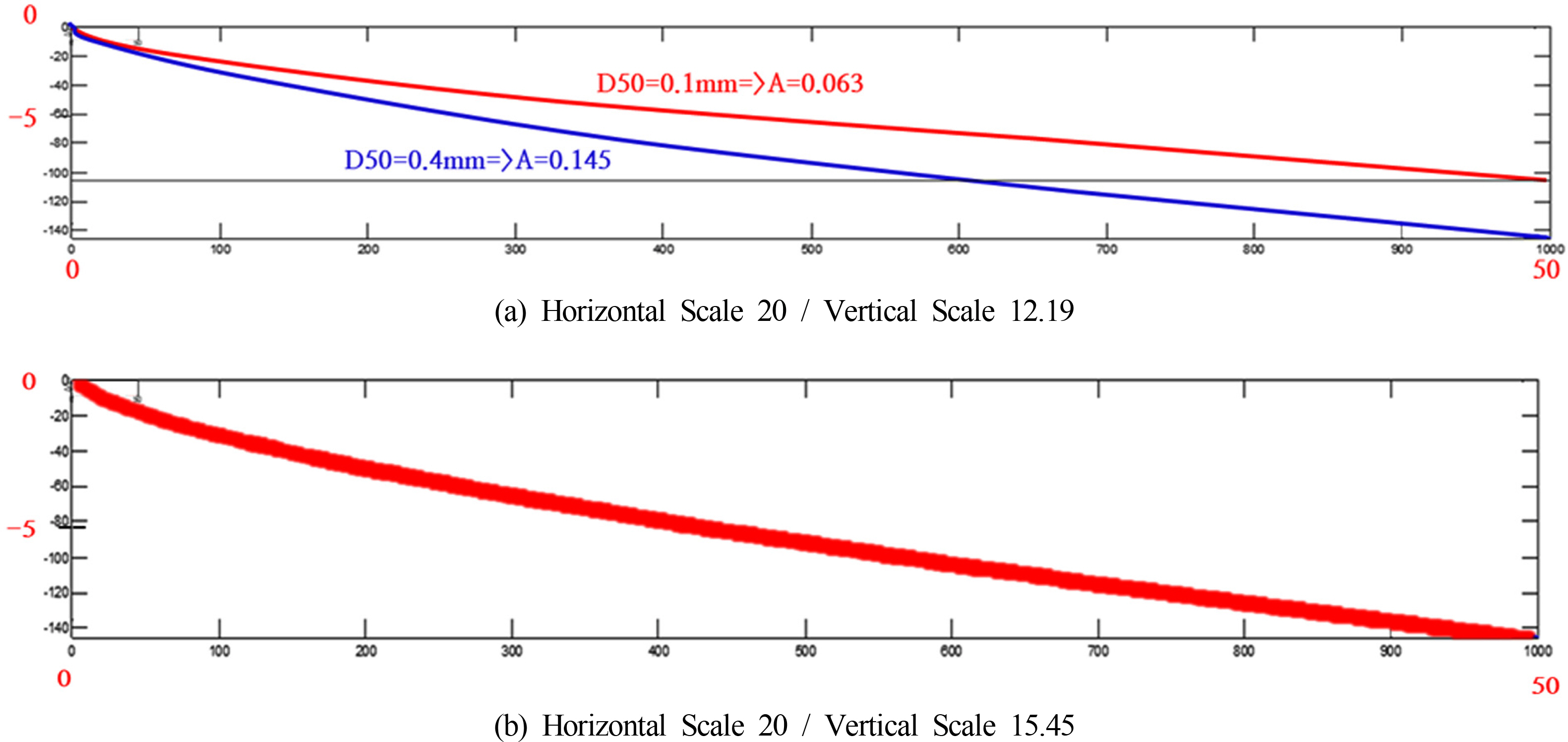
Fig. 15.
Comparison between physical model and prototype model by scale law of equilibrium beach profiles
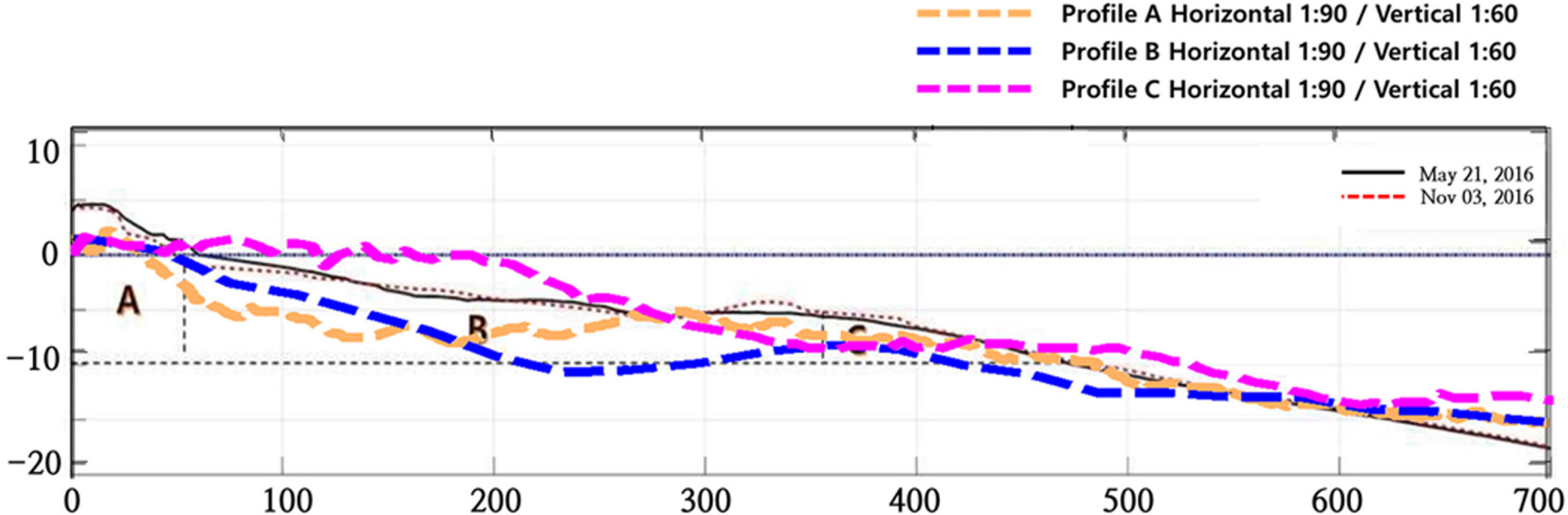
Table 1.
Classification of beach profile modeling Laws
| Author | Geometric Distortion | Hydrodynamic time scale (T) | Morphological time scale (t) |
|---|---|---|---|
| Vellinga (1982) |
|
|
nt = nT |
| Hughes (1983) |
|
|
nt = nT |
| Wang and Wang (1990) |
|
|
|
| Wang et al.(1994) |
|
|
nt = nT |
| Van Rijn(2010) |
|
|
nt = (nh)0.56 |
Table 2.
Scale factor in relation to median size
Table 3.
Classification of existing scaling laws
Table 4.
Comparison between Van Rijn’s and the present study
References
Cho, HJ., Choi, HG., Lee, TY., & Lee, . (2002). A Physical Model Test of Flood Level Changes by the Vegetation on the Floodplain of Urban River. Jourmal of Korea Water Resource Association, 35(2), 203-211.


Dean, RG. (1977). Equilibrium Beach Profiles: U.S. Atlantic and Gulf Coasts.. Department of Civil Engineering. Ocean Engineering Report 12, University of Delaware: Newark, Delaware.
Dean, RG. (1991). Equilibrium Beach Profile: Characteristics and Applications. Journal of Coastal Research, 7, 53-84.
Hur, DS. (2004). Deformation of Multi-Directional Random Waves Passing over an Impermeable Submerged Breakwater Installed on a Sloping Bed. Ocean Engineering, 31, 1295-1311.

Hughes, SA. (1983). Movable-bed Modeling Law for Coastal Dune Erosion. Journal of Waterway, Port, Coastal, and Ocean Engineering, 109(2), 164-179.

Hughes, SA., & Fowler, JE. (1990). Midscale Physical Model Validation for Scour at Coastal Structures. Technical Report CERC-90-8. US Army Engineer Waterways Experiment Station: Vicksburg, Mississippi.
Kwak, MS., Lee, KS., & Pyun, CK. (2003). Wave Field Analysis around Permeable Rubble-Mound Breakwaters. Korean Society of Coastal and Ocean Engineers, 15(2), 116-126.
Kim, TG., & Lee, JL. (2018). Analysis of Shoreline Response Due to Wave Energy Incidence Using Equilibrium Beach Profile Concept. Journal of Ocean Engineering and Technology, 32(2), 116-122.


Lee, JI., & Yoon, SB. (2006). Hydraulic and Numerical Experiments of Stem Waves along a Vertical Wall. The Korean Society of Civil Engineers, 26(40), 405-412.
Lee, JI., Choi, J., & Yoon, SB. (2008). Hydraulic Experiments of stem Waves along a Vertical Wall due to Unidirectional Random Waves. Korean Society of Coastal and Ocean Engineers, 20(1), 49-61.
Lee, WD., Her, DS., Park, JB., & An, SW. (2009). A Study on Effect of Beachface Gradient on 3-D Currents around the Open Inlet of Submerged Breakwaters. Journal of Ocean Engineering and Technology, 23(1), 7-15.
Miller, JK., & Dean, RG. (2004). A Simple New Shoreline Change Model. Coastal Engineering, 51(7), 531-556.

Oh, SH., Lee, KS., Jang, SC., & Lee, DS. (2011). Plane Experiments for Estimating Performance of the Sluice of Tidal Power Plant. Korean Society of Coastal and Ocean Engineers, 23(6), 474-481.


Wang, P., & Kraus, NC. (2005). Beach Profile Equilibrium and Patterns of Wave Decay and Energy Dissipation across the Surf Zone Elucidated in a Large-Scale Laboratory Experiment. Journal of Coastal Research, 21(3), 522-534.

Vellinga, P. (1982). Beach and Dune Erosion during Storm Surges. Coastal Engineering, 6(4), 361-387.

Van Rijin, LC. (2010). Coastal Erosion Based on the Concept of Sediment Cells.. EU-Project Conscience.: Delrares, Delft, The Netherlands.