유탄성 응답을 고려한 초대형 광탄 운반선(VLOC)의 피로 손상 예측 기법에 관한 연구
Study of the Prediction of Fatigue Damage Considering the Hydro-elastic Response of a Very Large Ore Carrier (VLOC)
Article information
Trans Abstract
Estimating fatigue damage is a very important issue in the design of ships. The springing and whipping response, which is the hydro-elastic response of the ship, can increase the fatigue damage of the ship. So, these phenomena should be considered in the design stage. However, the current studies on the the application of springing and whipping responses at the design stage are not sufficient. So, in this study, a prediction method was developed using fluid-structural interaction analysis to assess of the fatigue damage induced by springing and whipping. The stress transfer function (Stress RAO) was obtained by using the 3D FE model in the frequency domain, and the fatigue damage, including linear springing, was estimated by using the wide band damage model. We also used the 1D beam model to develop a method to estimate the fatigue damage, including nonlinear springing and whipping by the vertical bending moment in the short-term sea state. This method can be applied to structural members where fatigue strength is weak to vertical bending moments, such as longitudinal stiffeners. The methodology we developed was applied to 325K VLOC, and we analyzed the effect of the springing and whipping phenomena on the existing design.
1. 서 론
선체의 고유 진동수는 선체 길이가 증가 할수록 낮아지며 파도의 주파수에 근접하면 선체의 유탄성 현상인 스프링잉 현상이 발생한다. 대형 컨테이너 선박과 같은 고속 세장선에서 발생 빈도가 더욱 증가하며 대형 광탄 운반선과 같은 저속 비대선의 경우, 선체와 파도의 고유 주파수의 일치에 의한 공진 보다는 선수 형상에 따라 발생하는 파랑 회절력에 의해 진동 현상이 발생한다고 알려져 있으며 이러한 현상은 선체에 부가적인 피로 손상을 유발 시킬 수 있다. 최근 대형 선박의 발주에 있어서 유탄성 현상에 대한 관심이 높아지고 있으며 스프링잉 현상과 선수 및 선미에서의 강한 슬래밍에 의한 진동 응답인 휘핑 현상에 의한 피로 손상 예측에 관한 요구가 급격히 증가하고 있다. 선박의 유탄성 현상에 대한 수치적인 연구는 구조물의 응답과 구조물을 에워싸고 있는 유동장의 연성으로 가능하며 꾸준히 연구가 진행되어 오고 있다. Bishop et al.(1985)은 개단면 박판 보의 거동을 해석하기 위해 Euler, Timoshenko, Vlasov 등의 보 이론을 적용한 동적 계산을 수행하였으며, 실험 결과와의 비교를 통해 Timoshenko 및 Vlasov의 보 이론이 좋은 결과를 주는 것을 확인하였다. Malenica et al.(2007)은 그린 함수를 이용하여 주파수 영역에서의 스프링잉 응답 해석을 수행하였고 충격 응답 함수를 도입하여 시간 영역에서의 휘핑 응답에 대한 계산으로 확장하였으며, Remy et al.(2006)은 사파 중의 변형체 응답에 대한 모형 시험을 수행하였으며 모드 중첩법을 이용하여 주파수 영역에서 구한 응답을 비교하였다. Senjanovic et al.(2009)은 와핑 변형 및 막내 전단 변형의 효과를 고려한 1차원 보 요소를 개발하였으며 이를 폰툰형 바지 및 대형 컨테이너선에 대한 유탄성 계산에 적용하였다. Kim et al.(2009)과 Kim et al.(2012)은 직교 좌표계에서 3차원 랜킨 패널법(Rankine panel method)을 Vlasov 보 모델과 직접 연성하여 선형 및 비선형 응답 해석법을 개발하였고, 직접 연성을 수행하여 발생하는 수치적인 문제들을 해결하는 새로운 방법을 정립하였다. 위와 같이 유탄성 문제를 해석적으로 풀기 위한 연구는 꾸준히 진행되어 왔으나, 실제 선박의 설계에 적용할 수 있는 방법론과는 거리가 있다. Storhaug et al.(2011)은 모형 시험을 통해 저속 비대선에서의 스프링잉에 의한 피로 손상도를 추정하였고, Kim et al.(2018)은 대형 컨테이너 선박으로부터 계측된 실선 계측 데이터를 기반으로 변형률 데이터를 분석하여 선박이 경험한 진동 모드에 대한 분석을 수행하여 장기 피로 손상도를 추정하는 등 모형 실험과 실선 계측 데이터를 이용한 유탄성 응답에 대한 연구도 꾸준히 수행되고 있으나 이 또한 실제 설계 단계에 적용하기에는 한계가 있다.
본 연구는 파랑 하중에 의한 진동 성분인 스프링잉과 슬래밍 충격력에 의한 진동 성분인 휘핑과 같은 선박의 유탄성 응답을 수치적으로 계산하여 실제 초대형 광탄 운반선의 설계 단계의 피로 강도 평가에 적용할 수 있는 방법론을 개발하고 기존의 강체 기반의 피로 손상도와의 영향도를 평가하는 것을 목적으로 한다. 선형 및 비선형 기반의 방법을 적용하였으며 각각의 방법론에 대한 특징과 결과에 대하여 분석하였다.
선형 기반의 방법을 적용하는 경우, 3차원 전선 모델을 적용하여 주파수 영역에서 구조 부재의 응력 전달 함수(Stress transfer function)를 직접 구해, 광대역 피로 모델을 적용하여 구조 부재의 피로 손상도를 직접적으로 추정하였다. 비선형 기반의 방법을 적용하는 경우, 1차원 보 모델을 이용하여 시간 영역에서 유체-구조 연성 해석을 수행하였고, 해석이 수행될 주요 해상 상태는 기존의 설계 단계에서 계산되는 하중 전달 함수(Load transfer function)로부터 선정할 수 있는 방법을 적용하였다. 슬래밍을 고려한 선수파에서 해석을 수행하여 얻어지는 수직 굽힘 모멘트를 이용하여 대형 광탄 운반선의 종통재 연결부와 같은 길이 방향 부재의 유탄성 응답에 의한 피로 손상도의 비율을 추정하여 기존 설계 단계에서 계산되는 강체 기반의 보 이론에서 계산되는 피로 손상도에 고려하는 방법을 개발하여 초대형 광탄 운반선에 적용하여 결과를 분석하였다.
2. 피로 해석 절차
2.1 피로 손상 예측 방법
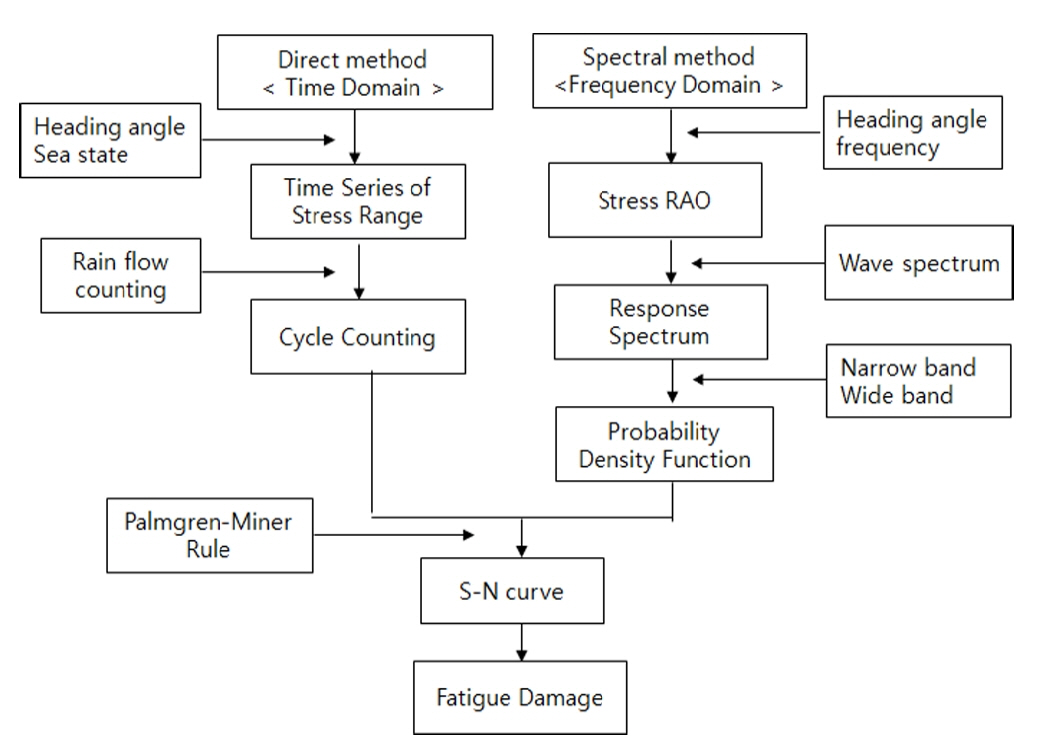
선박의 스프링잉 현상이 고려된 피로 손상도의 추정은 Fig. 1과 같이 크게 두 방법으로 나눌 수 있다. 첫째는 시간 영역에서 유체-구조 연성 해석을 수행하여 얻은 시계열을 레인플로우 집계법(Rainflow counting)과 같은 방법을 이용하여 응력 범위와 횟수를 직접 계산하는 방법이다. 이는 실제 구조물에 작용되는 하중 이력을 측정하여 도출되는 구조 응력 이력을 통해 유효한 빈도수를 집게하게 되며 도출된 응력 범위 분포 결과를 적절한 S-N 선도와 Palmgren-Miner의 선형 손상 누적 법칙을 이용하여 피로 수명을 예측한다. 응력의 응답과 횟수를 직접 집계하여 피로 손상을 계산하는 방법으로써 가장 신뢰할 만한 방법이지만, 통계적인 불확실성을 줄이고 안정한 피로수명의 예측을 위해 충분히 긴 지속시간을 가지는 다수의 응답 이력들이 필요하며 해상 상태 및 입사각의 개수를 전부 고려해 주려면 실제 적용시 시간과 비용에 대한 한계에 이를 수 있다. 물론 피로 수명에 주요한 영향을 미치는 몇 개의 해상 상태를 선정하고 피로 손상도에 가장 큰 기여도를 갖는 입사각으로 해석 개수를 줄이는 방법을 적용할 수 있으나 이것 또한 실제 접근에 한계가 있을 수 있다.
다른 방법으로는 환경 하중에 따른 구조응답에 대해 확률 통계적인 특성치를 이용하여 피로 수명을 예측 할 수 있는 주파수 영역에서의 피로 해석 방법이다. 스펙트럼 피로 해석법이라 불리며 비교적 정확하게 피로 수명을 예측할 수 있고 시간 영역에서의 피로 해석 방법에 비해 계산 시간상 효율적인 이점이 있으므로 선체의 피로 수명 평가를 위한 선급의 해석 지침서에서 많이 적용되는 방법이다. 이 방법은 먼저 운동 해석을 통해 하중 전달 함수를 계산하고, 구조 해석을 통하여 각 피로 계산 부위의 응력 전달 함수를 계산한다. 다음으로 파랑 스펙트럼(Wave spectrum)에 곱하여 응력 응답 함수(Response spectrum)를 계산하고 통계적 피로 해석 방법을 이용하여 주파수 영역에서 누적 피로 손상도를 계산한다. 여기서 선박을 강체로 가정하여 문제를 풀게 되면 현재 선급 및 조선소에서 사용하고 있는 선체의 피로 강도 평가 방법과 똑같은 방법이고, 유탄성 응답을 고려하여 광대역 피로 모델을 적용하면 선형 스프링잉 응답이 고려된 선체의 피로 수명을 계산할 수 있다.
2.2 유탄성 응답을 고려하는 피로 해석 절차의 개발
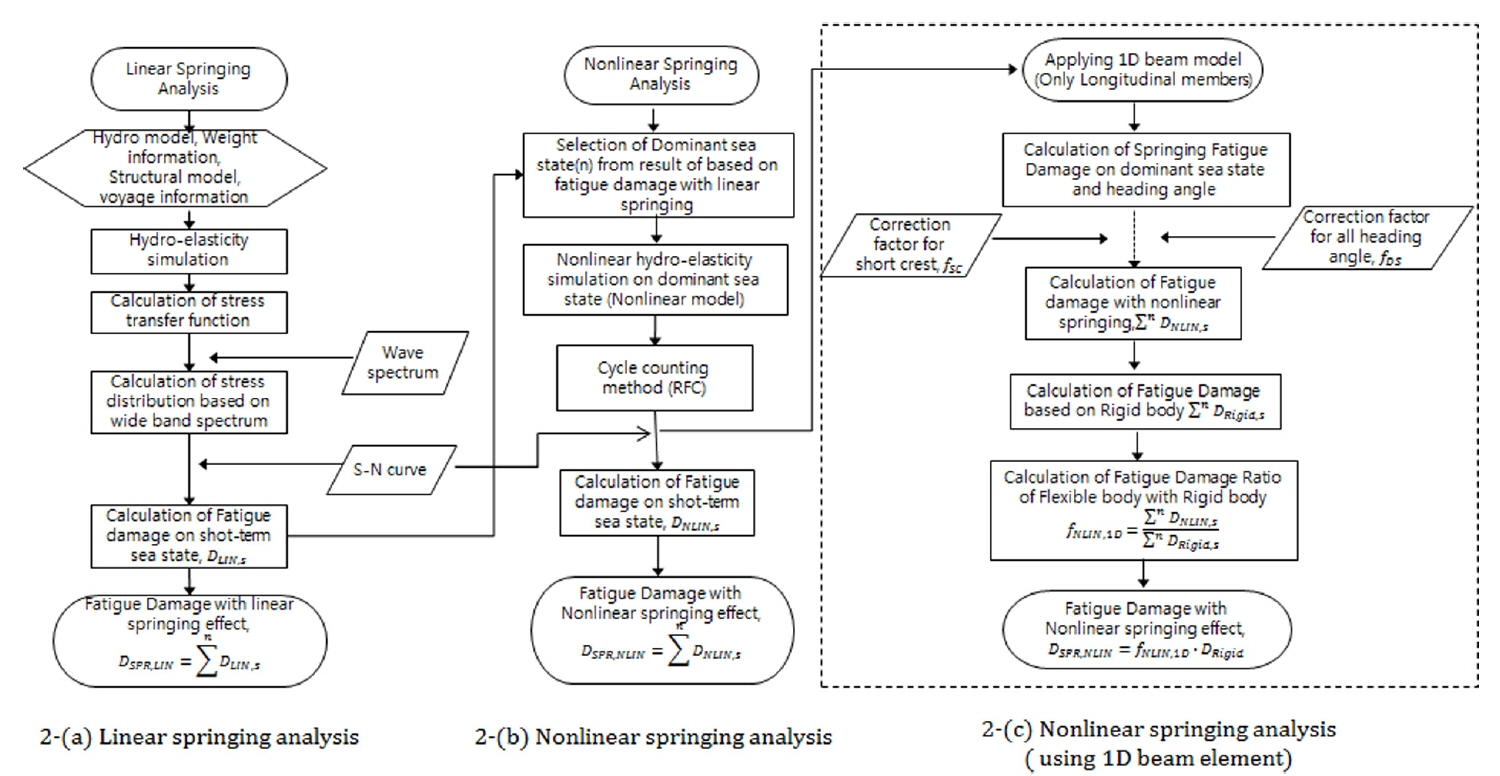
Fig. 2는 유탄성 응답을 고려하는 피로 손상도를 추정하는 해석 절차이다. Fig. 2에서 2-(a)는 선형 스프링잉 성분을 고려하는 피로 해석의 절차로써 앞장에서 설명한 주파수 영역 기반의 스펙트럼 피로 해석을 적용하는 방법이다. 3차원 구조 모델 기반으로 선박의 무게, 하중, 항해 정보를 이용하여 유탄성이 고려된 운동 해석을 수행하고 선형 스프링잉 성분이 포함된 단위파고에 대한 구조물의 응력 응답을 계산한다. 다음으로 광대역 스펙트럼을 가정한 응력 분포를 계산하여 각각의 단기 해상 상태에서의 피로 손상도를 구하고 해상 상태의 발현 확률을 고려하여 선형 스프링잉 성분이 고려된 장기 피로 손상도(DSPR, LIN)를 추정한다. 유탄성 해석의 응답치는 고주파수 영역의 진동 응답이 포함되어 응력 응답 스펙트럼이 광대역 분포를 보인다. 따라서 협대역이 아닌 광대역 가정을 통한 단기 해상 상태의 피로 손상도 계산이 필요하며, 이에 대한 고려를 위하여 본 연구에서는 Benasciutti and Tovo(2005)가 제시한 광대역 수정 모델을 적용하였다. 이 모델은 협대역 응답 스펙트럼으로 가정하여 얻어진 피로 손상도로부터 광대역 스펙트럼 수정 계수를 적용하는 방법으로써, 이에 대한 자세한 방법 및 적용 결과에 대하여 다수의 연구에서 확인할 수 있다(Choung et al., 2012; Park et al., 2011). 유탄성 해석을 수행하여 각각의 핫스폿 위치에서 단위파고에 대한 응력 전달 함수만을 얻으면 되므로, 해석 시간이 많이 소요 되지 않는다. 또한 높은 파고와 선박의 기하하적인 형상에 의한 비선형성이 강하게 나타나지 않고, 슬래밍의 발생 확률이 낮은 잔잔한 해상 상태를 주로 운항하는 선박에 적용한다면 피로 손상도 추정에 효율적인 방법이라 할 수 있다.
Fig. 2의 2-(b)는 슬래밍에 의한 휘핑 및 비선형 스프링잉을 고려하는 피로 해석 절차이다. 안정한 피로 수명 계산을 위하여 파랑 분포도 내의 모든 단기 해상 상태의 시간 영역에서 유탄성 해석을 수행해야 하지만 실제 접근에 한계가 있다. 따라서 피로 손상도에 주요한 영향을 미치는 해상 상태를 선정하여 유탄성 해석을 수행해야 하며 이는 앞선 선형 스프링잉 해석의 결과로부터 선정할 수 있다. 즉, 각각의 핫스폿 위치에서 계산되는 장기 피로 손상도에 주요한 영향을 미치는 주요 해상 상태들을 선정하여 비선형 유탄성 해석을 수행한다. 여기서 얻은 응력의 시계열을 레인플로우 집계법과 같은 방법을 사용하여 응력의 범위와 빈도수를 집계하여 S-N 선도에 적용하여 피로 손상도를 추정한다. 모든 해상 상태와 전 방향 입사각에 대하여 계산하면 가장 정확한 피로 손상도를 예측할 수 있지만, 실제 설계 단계에서는 시간적으로 제약이 많은 접근법이다.
따라서 2-(c)와 같이 1차원 보 모델을 이용하여 효과적으로 휘핑 및 비선형 스프링잉 성분을 고려할 수 있는 피로 해석 절차를 제시하였다. 1차원 보 모델은 핫스폿 위치의 응력 응답을 직접 계산하지 않는 대신 시간 영역에서 선체의 수직 굽힘 응답(Vertical bending response)을 3차원 전선 모델에 비하여 효율적으로 계산할 수 있기 때문에 수직 굽힘 응답이 피로 손상에 주요한 영향을 미치는 종통재 보강재 연결부(Longitudinal connections)와 같은 구조 부재에 적용할 수 있다. 설계 단계에서 종통재 보강재 연결부의 피로 손상도는 내외부 압력 및 가속도 등을 고려하고 보 이론을 적용하여 강체 기반의 피로 손상도를 비교적 정확히 계산할 수 있다. 여기서 계산되는 피로 손상도는 수직 굽힘 응답에 지배적이며, 대형 광탄 운반선의 유탄성 응답 또한 수직 굽힘 응답에 지배적이라 예상되므로 1차원 보 모델에서 계산되는 수직 굽힘 모멘트를 피로 손상도 추정에 사용할 수 있다.
일반적으로 선체 구조의 피로 손상도는 휘핑이나 스프링잉과 같은 고주파수 대역의 진동 응답보다 파랑 하중에 의한 저주파수 대역의 강체 응답이 주요하다고 알려져 있다. 또한 피로 손상도의 계산을 위한 장기 해석(Long-term analysis)은 파랑 분도 내의 해상 상태의 발현 확률에 매우 의존적이며, 비선형성이 강하게 나타날 수 있는 높은 유의 파고를 갖는 해상 상태의 발현 확률은 상대적으로 매우 낮다. 즉 장기 해석 후의 피로 손상도에 주요한 영향을 미치는 해상 상태는 강체 기반에서 계산된 값과 유탄성 기반에서 계산된 값이 유사할 것으로 예측되기 때문에 유탄성 해석이 수행 될 주요 해상 상태는 설계 단계에서 계산되는 수직 굽힘 모멘트 전달 함수를 이용할 수 있다.
수직 굽힘 모드에 주요한 영향을 미치는 선수파(Head sea) 조건에서 해석을 수행하고, 단면 계수와 응력 집중 계수를 적용하여 수직 굽힘 모멘트 시계열을 응력의 시계열로 수정하면, 레인플로우 집계법을 적용하여 응력의 범위와 빈도수를 집계하여 피로 손상도를 추정할 수 있다. 여기서 계산되는 값은 수치 계산을 위한 일 방향파(Long-crested wave)가 적용된 피로손상도이므로, 이를 실제 해상의 파(Short-crested wave)에 대하여 적용할 필요가 있다. fs(θ)=kcos2(θ)로 정의되는 퍼짐 함수(Spreading function)를 아래의 식 (1)과 같이 적용하였다.
θ0 : 주요 파 입사각
θ : 주요 파 입사각 주위의 상대적 퍼짐(Relative spreading)
식 (1)의 퍼짐 함수를 적용하기 위하여 주요 파 입사각에 대한 각각의 피로 손상도가 필요하며 이는 앞서 주요 해상 상태의 결정을 위한 응력 전달 함수를 이용할 수 있다. 즉, 이 응력 전달 함수를 이용하여 스펙트럼 해석을 수행하고 주요 파 입사각에 대한 각각의 피로 손상도를 계산하여, 이를 퍼짐 함수에 적용하면 일 방향파와 실제 해상의 파에 대한 피로 손상도의 비율(fSC)을 추정할 수 있다. 또한 여기서 계산된 각 주요 입사각에 대한 각각의 피로 손상도는 선수파 만을 주요 입사각으로 적용할 경우와 전 방향의 파 입사각을 피로 손상도 계산에 적용했을 때의 피로 손상도 비율(fDC)을 구하는데도 적용할 수 있다. 마지막으로 저주기 필터 등을 적용하여 진동 성분이 제거된 응답의 피로 손상도를 계산하여 유탄성 응답에 의한 피로 손상도 증가분(fNLIN, 1D)을 추정한다. 이 값을 강체 기반의 피로 손상도(DRigid)에 고려해주면 비선형 스프링잉 및 휘핑 응답에 의한 종통재 보강재 연결부의 피로 손상도를 추정할 수 있다.
3. 실선 유탄성 해석
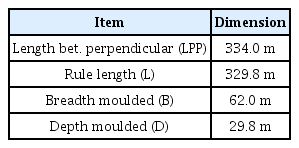
해석에 사용된 모델은 325,000DWT 초대형 광탄 운반선이며 주요 제원은 Table 1과 같다.
유탄성 해석에 적용된 하중 조건은 평형수 조건(Normal ballast condition)과 최대 화물 적재 조건(Full loading condition)이며, 점성 감쇠 계수는 5%, 구조 감쇠 계수는 동일한 타입의 선박에 대하여 모형실험을 수행하고 결과를 제시하였던 기존의 참고문헌을 따라 0.5%를 적용하였다(Storhaug et al., 2011).
3.1 수치 해법
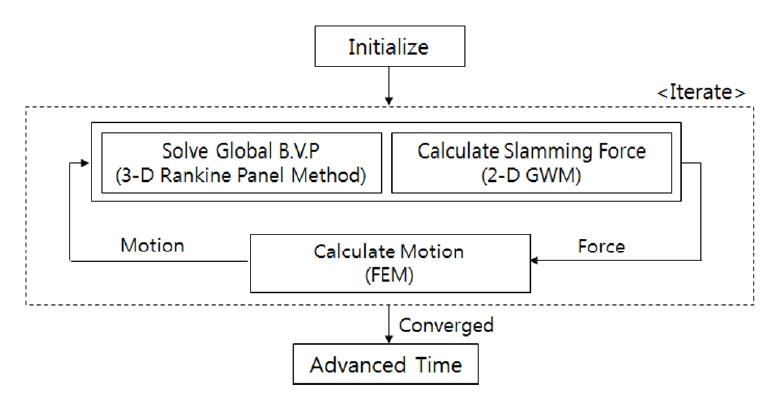
선체의 유탄성 응답을 예측하기 위하여 시간 영역에서 유체-구조 연성 문제를 정립하여 풀어야 한다. 본 연구에 사용된 프로그램은 유체 영역에서 3차원 포텐셜 유동을 가정하고 경계 요소법(Boundary element method)을 적용하여 그 해를 구하고, 경계치 문제는 평균 위치에서의 선형화된 경계 조건을 이용하는 WISH-FLEX(Kim and Kim, 2011)이다. 시간 영역에서의 유탄성 해석은 기하하적 비선형성의 고려를 위해 실 접수 면적에 대하여는 Froude-Krylov(F-K) 및 유체 정하중을 고려하는 약 비선형법(Weakly-nonlinear method)을 적용하였으며, 슬래밍 하중의 계산은 Generalized wagner model(GWM)을 적용하였다. 이 모델은 유체동역학적 압력을 속도의 제곱에 비례하는 슬래밍 압력과 가속도에 비례하는 부가질량 압력으로 구성하여 두항을 서로 독립적으로 표현하여 초기 조건 문제의 해를 구하였으며, 평판의 입수 문제에 대한 해석적 해와 임의의 형상으로부터의 등각 사상 함수를 통하여 해를 구하는 방법을 적용하였다(Khabakhpasheva et al., 2014). 선체의 운동 방정식은 아래의 식 (2)-(3)과 같이 3차원의 직교 좌표계에서 정의할 수 있다.
M, C, K는 각각 선체의 질량, 감쇠, 강성행렬이고 t는 시간
3.2 선형 스프링잉에 의한 피로 손상도 추정
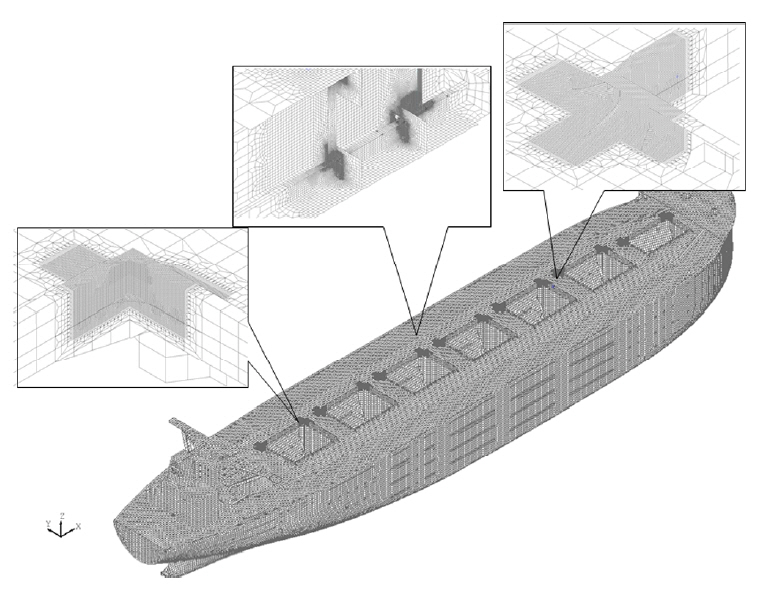
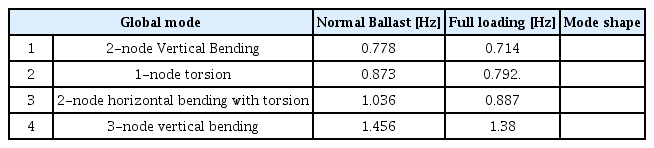
Fig. 4는 피로 손상도 계산을 위한 3차원 전선 모델이며, Table 2는 모드 해석을 수행하여 얻은 하중 조건에서의 저차 고유 모드와 해당 주파수이다. 각 고유 모드에 대한 핫스폿 위치에서 응력을 미리 계산하고 유탄성 해석을 통하여 각 고유 모드의 응답치(Amplitude)를 얻어 모드 중첩법(Superposition method)을 이용하면 선형 스펙트럼 방법에 적용되는 응력 전달 함수를 빠르게 계산할 수 있다.
스펙트럼 방법의 계산에서 중요한 파라미터들은 선박의 응답 스펙트럼으로부터 계산되며, 이는 입사각과 전진 속도에 의존하는 응력 전달 함수(H(ωe|θ))와 유의 파고(Hs), 영점 교차주기(Tz)로 대표되는 파 스펙트럼(Sη(ω|Hs, Tz))으로 표현이 가능하다. 선박이 U0의 속도로 전진하는 경우 응력 전달 함수는 조우주파수로 표현이 되어야 하며 이는 식 (4)와 같이 표현할 수 있다. U0의 속도로 장파봉파를 입사각 μ0로 전진하는 선박이 경험하는 조우 주파수(Encounter frequency)는 식 (5)로 주어지며 ωe는 조우주파수, g는 중력가속도를 의미한다.
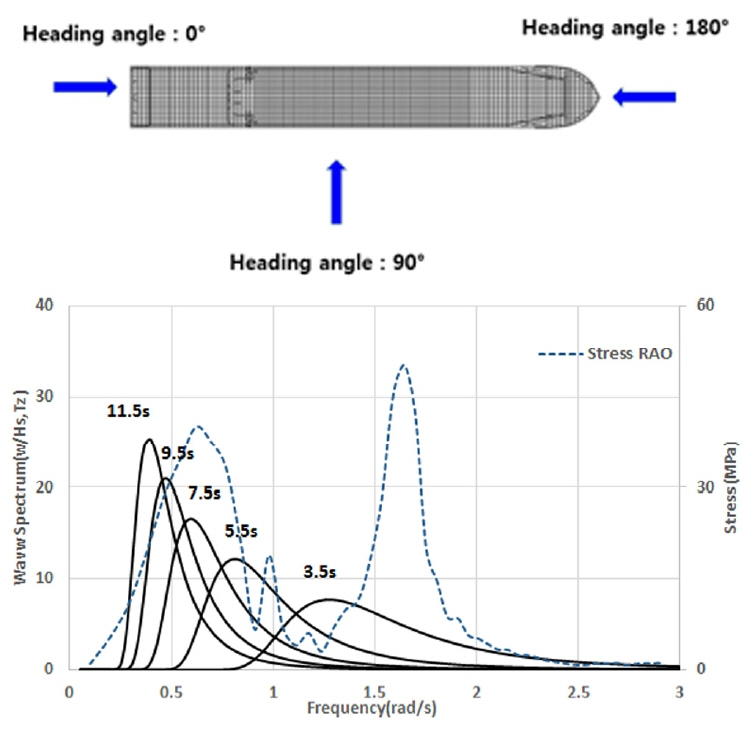
응답 스펙트럼의 특성을 살펴보기 위하여 Fig. 5와 같이 영점 교차 주기에 따른 파랑 스펙트럼과 선수파(μ0=180°)를 적용한 종통재 연결부의 대표적인 응력 전달 함수를 나타내었다. 응력 전달 함수 계산에 적용된 선속은 설계 속도의 2/3이다. 파랑 스펙트럼의 에너지는 영점 교차 주기가 점차 짧아질수록 작아지고, 스프링잉의 공진 주기는 약 1.7rad/sec의 고주파수 영역에 머물러 있는 것을 확인할 수 있다. 고주파수 영역의 파랑에너지는 저주기 응답(0.1-1.0rad/s)의 파랑 에너지에 비하여 매우 작다. 응력 전달 함수가 저주파수 영역보다 고주파수 영역에서 크고, 이 응답치의 제곱에 비례하여 응답 스펙트럼이 계산되지만, 파랑 스펙트럼의 에너지 차이로 인하여 스프링잉과 같은 고주파수 영역에서 계산되는 응답 스펙트럼은 저주파수 영역보다 매우 작게 계산된다. 이는 고주파수의 진동 응답보다 파도에 의한 저주파수 대역의 응답이 피로 손상에 훨씬 더 많은 기여를 한다는 의미이다.
선박이 선수 방향에서 파도를 조우하며 전진하는 경우(90°<μ0<270°)에 식 (4)와 같이 조우 주파수의 영향으로 스프링잉의 공진 주파수가 짧아지며, 큰 에너지를 갖는 파랑 스펙트럼과의 교차면을 발생시켜 응답 스펙트럼에서의 스프링잉 성분에 의한 계산을 크게 한다. 이와는 반대로 측면파(Beam sea)나 선미파(Following sea)를 조우하며 전진하는 경우 공진 주파수가 변하지 않거나 길어진다. 피로 손상도 계산에 적용되는 파랑 분포도 내의 가장 짧은 주기를 갖는 해상 상태가 3.5초임을 감안하면, 선수파의 조건에서 약 1.2rad/s 보다 짧은 주파수에서 피크를 갖는 스프링잉이 발생되어야 이 성분이 식(4)의 응답 스펙트럼 계산에 기여하여 선형 스프링잉에 의한 피로 손상도를 계산할 수 있다.
Fig. 5에 나타낸 응력 전달 함수의 위치인 종통재 보강재 연결부에 대하여 모든 입사각을 고려한 장기 피로 손상도를 Fig. 6과 같이 나타내었다. 선수파에서 스프링잉 응답의 공진 주파수가 약 1.7rad/s 근처에 존재하고, 그 외의 입사각에서는 조우 주파수를 고려하였을 때 더 높은 주파수 영역대에서 공진이 발생하므로 해상 상태와 무관하게 전체 피로 손상도에서 선형스프링잉 성분이 차지하는 기여도는 약 1% 미만으로 아주 작게 계산된다. 이러한 경향은 Fig. 4의 해치 코너를 포함한 다른 모든 핫스폿 부위도 동일한 경향을 나타낸다. 이를 통하여 상대적으로 높은 주파수 영역대에서 공진이 발생하는 대형 광탄 운반선의 선형 스프링잉 성분은 피로 손상도 계산에 거의 기여를 하지 않는 것을 알 수 있다.
3.3 비선형 스프링잉 및 휘핑에 의한 피로 손상도 추정
여기서는 Fig. 2의 2-(c)에 설명되어 있는 1차원 보 모델을 이용하는 방법을 적용한다. Table 2에 나타낸 고유모드 해석을 통하여 파도와의 공진 가능성은 2절점 수직 굽힘 모드에서 가장 먼저 발생되는 것으로 예상되며, 이는 스프링잉 응답의 발생 가능성이 2절점 수직 굽힘 모드에서 가장 크다고 할 수 있기 때문에 이 모드에 가장 취약할 것으로 예상되는 종통재 연결부에 이 방법을 적용한다. 대형 컨테이너선과 마찬가지로 초대형 광탄 운반선 역시 큰 개구부를 갖기 때문에 비틀림(Torsion)을 고려해야할 필요성이 있으며 이상화된 1차원 보 모델은 횡굽힘을 고려한 Vlasov 보 이론에 기반을 한다. 선박의 횡격벽(Transverse bulkhead)의 위치에 절점을 설정하고 각 절점 사이에서 대표되는 단면 정보를 추출하였다. Fig. 7과 같이 3차원 전선 모델을 1차원 보이론 모델로 치환하여 계산할 때 보 모델에 적용되는 성분은 아래와 같다.
- Area, Shear Area, Second moment of Area
- Torsional Constant, Warping Constant, Shear Constant
- Neutral Axis, Center of Gravity, Mass
- Polar mass moment of Inertia, Second moment of Inertia, Warping Inertia
이상화된 1차원 보이론 모델과 3차원 전선 모델의 동적 특성의 등가성 확인을 위하여 1차원 모델에 대하여 모드 해석을 추가로 수행하였다. Table 3과 같이 각 구조 모델의 비 접수 조건에서 가장 낮은 차수에서 발생되는 수직 굽힘 모드와 비틀림 모드의 결과가 상당히 일치하는 것을 보아 1차원 보이론 모델이 3차원 모델의 정보를 잘 반영하는 것을 확인 할 수 있다.
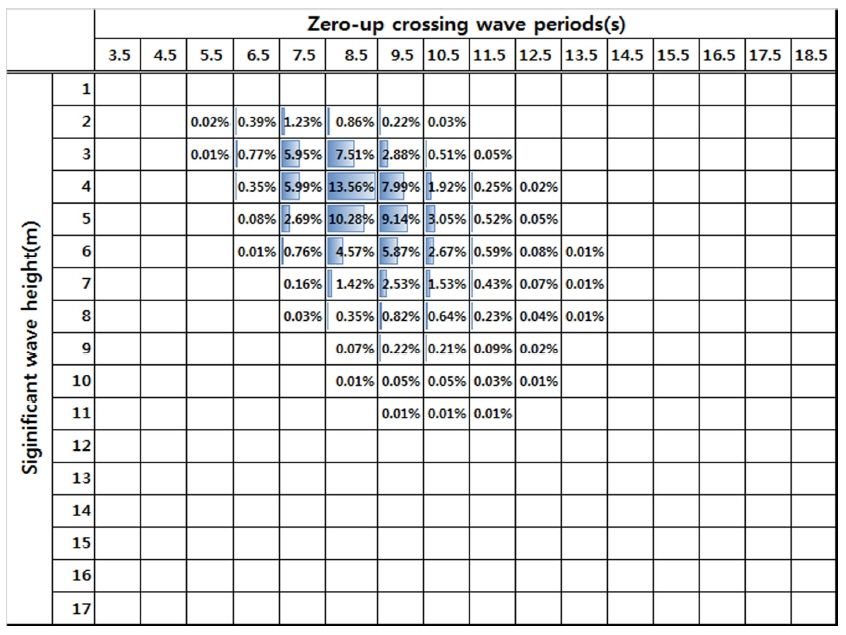
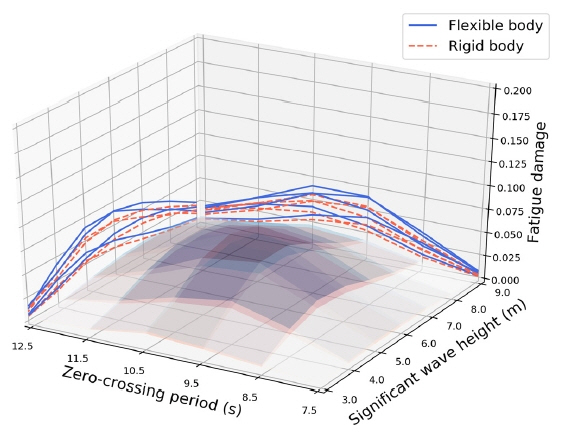
다음으로 유탄성 해석을 수행할 주요 해상 상태를 선정해야 한다. 수직 굽힘 모멘트 전달 함수로부터 치환된 응력 전달 함수가 선체 중앙부 종통재 연결부를 대표한다고 가정하여 장단기 피로 해석을 수행하면 Fig. 8과 같이 각각의 단기 해상 상태에 대한 피로 손상도를 추정할 수 있다. 대상 선박의 경우 영점 교차 주기가 6.5초에서 11.5초, 유의 파고가 3m에서 9m까지의 해상 상태가 전체 피로 수명의 95% 이상을 차지하는 것으로 추정되며 이 해상 상태에 대하여 슬래밍을 고려한 비선형 유탄성 해석을 수행하였다.
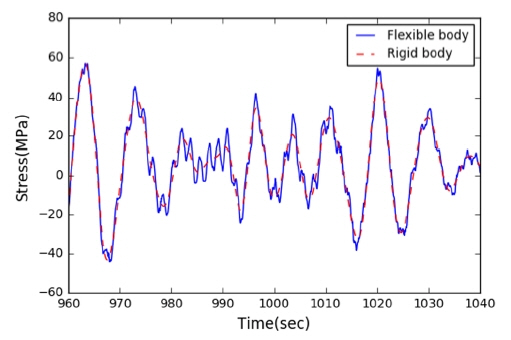
1차원 보 모델을 이용하는 경우 핫스폿 위치에서의 응력을 직접 계산할 수 없기 때문에 유탄성 응답이 고려된 피로 손상도를 직접 추정하는 대신, 피로 손상도에 대한 기여분을 계산하여 강체 기반의 피로 손상도에 고려해 주는 방법을 취한다. 따라서 유탄성 응답이 포함되지 않은 시계열이 필요하며, 본 연구에서는 저주기 필터를 사용하여 이 응답을 얻었다. Fig. 9는 선체 중앙부에서의 비선형 수직 굽힘 모멘트의 시계열에 선체의 단면 계수와 응력 집중 계수를 적용하여 치환된 응력의 시계열(Flexible body)과 저주기 통과 필터를 통과한 시계열(Rigid body)을 함께 표시한 예이다.
Fig. 10과 Fig. 11은 주요 단기 해상 상태에서 일 방향파와 선수파만을 적용한 선체 중앙부에서의 장기 피로 손상도이다. 일방향파로 계산된 피로 손상도를 실제 해상의 파에 대하여 적용하기 위한 수정 계수는 약 0.82로 계산되었고, 선수파만을 적용한 피로 손상도를 전방향 주요 파 입사각에 대하여 확대하기 위한 수정 계수는 약 0.41로 계산된다. 각각의 해상 상태에서 계산된 피로 손상도에 앞에서 계산된 각각의 수정 계수를 고려하면 최종 피로 손상도를 추정할 수 있다. 대상 선박의 경우 종통재 연결부에서 유탄성 응답을 고려하였을 때, 강체 기반의 피로 손상도 대비 약 25%가 증가되는 것으로 추정되며 이 피로 손상도 증가분은 S-N 선도의 역기울기를 이용하면 수직 굽힘 모멘트에 의한 발생되는 유탄성 응답으로 인한 응력의 증가분을 추정할 수 있다.
위에서 추정된 유탄성 응답에 의한 피로 손상도의 증가분을 강체 기반의 피로 손상도가 가장 크게 계산되는 갑판의 종 방향 연결부에 적용하면 피로 손상도가 0.49에서 0.61로 증가하며 이는 설계 수명을 만족하는 결과를 제시한다.
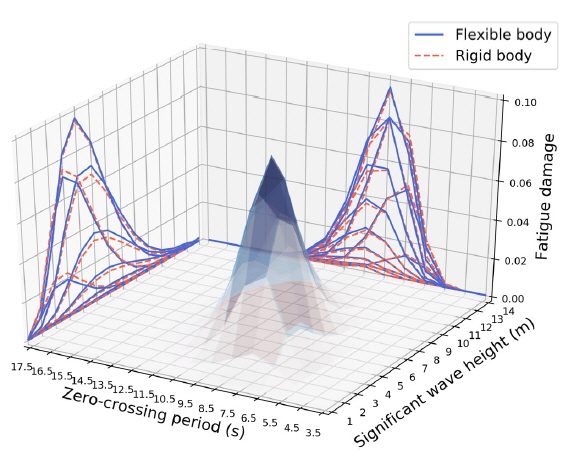
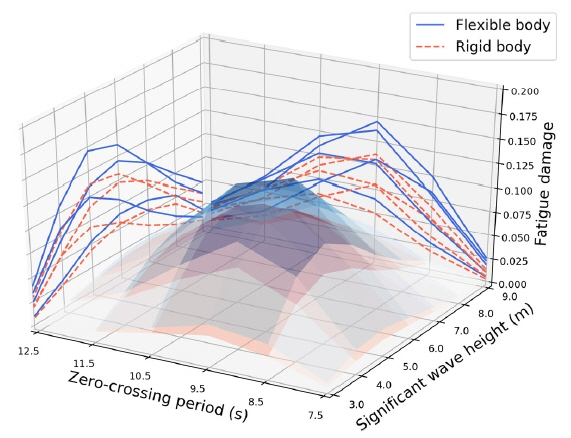
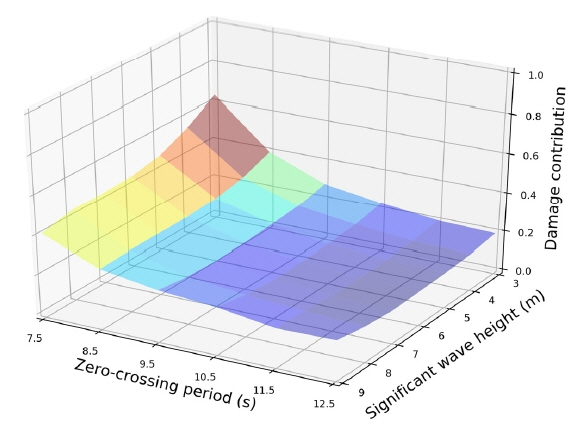
다음으로 각각의 단기 해상 상태에서 계산되는 피로 손상도의 특성을 확인하기 위하여 Fig. 12와 같이 각각의 해상 상태에서 계산되는 유탄성 응답이 포함된 장기 피로 손상도를 정규화(Normalize)하여 각각의 단기 해상 상태에서 계산되는 총 피로 손상도에서 유탄성 응답이 차지하는 비율을 식 (6)과 같이 계산하였다. Fig. 12와 같이 영점 교차 주기가 짧고 유의 파고가 낮은 해상 상태일수록 피로 손상도의 절대값은 매우 작지만 유탄성 응답에 의한 피로 손상도의 비율이 큰 것을 확인하였다.
4. 결 론
본 연구에서는 선박의 유탄성 응답을 고려한 초대형 광탄 운반선의 피로 강도 평가를 수행할 수 있는 절차를 개발하고 실선에 적용하여 영향도를 평가하였다.
선형 스프링잉 해석의 경우 3차원 전선 모델을 적용하고 모드 중첩법을 이용하여 각각의 핫스폿 부위의 응력 전달 함수를 직접 구할 수 있었으며, 광대역 스펙트럼을 적용하여 선형 스프링잉이 고려된 피로 손상도를 추정할 수 있었다. 선형 스프링잉에 의한 피로 손상도의 증가는 거의 없는 것으로 계산되며 이는 기존의 타 연구와 같은 결과이다.
휘핑과 비선형 스프링잉을 고려할 경우 주요 해상 상태의 시간 영역에서 추정할 수 있으며 많은 해상 상태와 입사각을 고려하여 계산하므로 설계단계에서 적용하기에는 비효율적이다. 따라서 1차원 보 모델을 이용하여 종통재 연결부와 같은 수직 굽힘 모멘트에 취약한 부위에 대하여 휘핑 및 비선형 스프링잉을 고려할 수 있는 해석 방법을 제시하였다.
수직 굽힘 모멘트 전달 함수로부터 피로 손상도에 주요한 영향을 미치는 해상 상태를 선정하여 선수파에 대하여 유체-구조 연성 해석을 수행하여 얻어진 선체 중앙부에서의 수직 굽힘모멘트를 이용하여 피로 손상도를 추정하였다. 고주파수 대역의 진동 응답을 제거하여 강체 응답을 얻었으며 이로부터 계산되는 피로 손상도의 비율을 유탄성 응답에 의한 피로 손상도 증가분으로 추정하여 설계 단계에서 적용되는 보이론 기반의 결과에 적용하여 종통재 연결부에서 유탄성 응답 의한 최종 피로손상도를 계산할 수 있었다. 선형 방법으로 계산되지 않았던 유탄성 응답에 의한 피로 손상도의 증가분이 계산되었으며 이는 초대형 광탄 운반선의 경우 비선형 성분이 피로 손상도에 주요한 영향을 미치는 것을 확인할 수 있다.
본 연구는 설계 단계에서 적용할 수 있는 해석 절차의 개발과 절차 적용에 따르는 설계 효과를 파악하는 것이 목적이었으며, 추후 주요 해상 상태와 주요 입사각의 변화에 따르는 유탄성 응답이 고려된 피로 손상도의 추정과 비선형 스프링잉 성분의 원인 및 분석과 같은 꾸준한 연구가 필요할 것으로 사료된다.