|
 |
- Search
| J. Ocean Eng. Technol. > Volume 33(1); 2019 > Article |
|
Abstract
Drilling mud was used once in the step of separating the gas and powder they were transported to a surge tank. At that time, the fine powder, such as dust that is not separated from the gas, is included in the gas that was separated from the mud. The fine particles of the powder are collected to increase the density of the powder and prevent air pollution. To remove particles from air or another gas, a cyclone-type separator generally can be used with the principles of vortex separation without using a filter system. In this study, we conducted numerical simulations of air-particle flow consisting of two components in a cyclone separator in a mud handling system to investigate the characteristics of turbulent vortical flow and to evaluate the collection efficiency using the commercial software, STAR-CCM+. First, the single-phase air flow was simulated and validated through the comparison with experiments (Boysan et al., 1983) and other CFD simulation results (Slack et al., 2000). Then, based on one-way coupling simulation for air and powder particles, the multi-phase flow was simulated, and the collection efficiency for various sizes of particles was compared with the experimental and theoretical results.
эХ┤ьГБьЧРьДЬ ьДЭьЬа ы░П ъ░АьКдые╝ ьЛЬь╢ФэХа ыХМ, ыУЬыж┤ы╣ДэК╕(Drill bit)ьЭШ ьЬдэЩЬ ы░П ыГЙъ░БьЮСьЪйъ│╝ эХиъ╗Ш ьЩ╕ы▓╜ьЭ┤ ым┤ыДИьзАьзА ьХКъ▓М ьХХыаеьЭД ьЬаьзАьЛЬь╝Ььг╝ыКФ ьЧнэХаьЭД эХШыКФ ыи╕ыУЬ(Mud)ъ░А ьВмьЪйыРШый░, ьЭ┤ыЯмэХЬ ыи╕ыУЬьЭШ ьИЬэЩШ, ьЮмь▓Шыжм, ьаАьЮе ыУ▒ьЭШ ьЧнэХаьЭД эХШыКФ ыи╕ыУЬ эХ╕ыУдызБ ьЛЬьКдэЕЬ(Mud handling system)ьЭ┤ эХДьЪФэХШыЛд. ьЭ╝ы░ШьаБьЬ╝ыбЬ ыи╕ыУЬ эХ╕ыУдызБ ьЛЬьКдэЕЬьЭД ьЭ┤ьЪйэХШьЧм эЪМьИШыРЬ ыи╕ыУЬьЧРыКФ ызИьЭ┤эБмыбЬ ыЛиьЬДьЭШ ып╕ьД╕эХЬ ы╢Дь▓┤ъ░А ьб┤ьЮмэХШъ│а ьЮИьЬ╝ый░, ьЭ┤ыЯ░ ы╢Дь▓┤ыКФ ьЮеы╣ДьЧР ьЖРьГБьЭД ьдД ьИШ ьЮИъ╕░ ыХМым╕ьЧР ьаБьаИэЮИ ы╢ДыжмыРШьЦ┤ьХ╝ эХЬыЛд. ьЭ┤ые╝ ы╢ДыжмэХШыКФ ьЮеы╣ДыбЬыКФ ы░▒эХДэД░(Bag filter), Electrofilter ъ╖╕ыжмъ│а ьЫРьЛмы╢Дыжмъ╕░(Centrifugal separator ыШРыКФ Cyclone separator)ъ░А ьЮИыЛд. ьЭ┤ ьдС ьЫРьЛм ы╢Дыжмъ╕░ыКФ ыМАъ▓М ьЫРь╢ФэШХьГБьЭШ ыЛиьИЬэХЬ ъ╡мьб░ые╝ ъ░АьзАый░ ьЬаьЮЕыРЬ эШ╝ьГБыеШьЭШ ьДаэЪМыбЬ ьЭ╕эХЬ ьЫРьЛмыаеьЭД ьЭ┤ьЪйэХШьЧм ы╢Дь▓┤ьЩА ыи╕ыУЬые╝ ы╢ДыжмэХШъ▓М ыРЬыЛд. ьЭ┤ыЯмэХЬ ьЫРьЛмыаеьЭД ьЭ┤ьЪйэХЬ ыЛдьГБ ы╢Дыжмъ╕░ыКФ ьДдь╣Ш ы░П ьЬаьзАы╣ДьЪйьЭ┤ ьЮСъ│а эЪиьЬиьЭ┤ ьвЛъ╕░ ыХМым╕ьЧР ыЖНьЧЕьЧРьДЬ ъ│╡ьЧЕъ╣МьзА ьЧмыЯм ьВ░ьЧЕьЧРьДЬ ыЛдьЦСэХШъ▓М ьВмьЪйыРШъ│а ьЮИьЬ╝ый░, эК╣эЮИ ып╕ъ╡нъ│╝ ьЬаыЯ╜ ыУ▒ьЧРьДЬ ызОьЭА ьДаэЦЙьЧ░ъ╡мъ░А ьЭ┤ыгиьЦ┤ьа╕ьЩФыЛд.
ьзАъ╕Иъ╣МьзА ьЫРьЛм ы╢Дыжмъ╕░ьЧР ыМАэХЬ ьДаэЦЙьЧ░ъ╡мыбЬ, Boysan et al.(1983)ьЭА LDA(Laser doppler anemometry)ые╝ ьЭ┤ьЪйэХЬ ы░йы▓ХьЬ╝ыбЬ ьЫРьЛмы╢Дыжмъ╕░ ыВ┤ы╢АьЭШ ь╢Х ы░йэЦеъ│╝ ьаСьДаы░йэЦеьЭШ ьЖНыПДьД▒ы╢ДьЭД ьЛдэЧШьЭД эЖ╡эХ┤ ь╕бьаХэХШьШАьЬ╝ый░, Slack et al.(2000)ьЭА ьГБьЪй эФДыбЬъ╖╕ыЮиьЭ╕ FLUENTые╝ ьЭ┤ьЪйэХШьЧм Boysan et al.(1983)ьЭШ ьЛдэЧШьЧРьДЬ ь╕бьаХыРЬ ыВ┤ы╢АьЖНыПД ьД▒ы╢ДыУдьЭД ы╣Дъ╡Р ы╢ДьДЭэХШьШАъ│а, ыВЬыеШыкиыН╕ьЧР ыФ░ые╕ ьИШь╣Ш ьЛЬыомыаИьЭ┤ьЕШьЭШ ьаХэЩХыПДьЧР ыМАэХ┤ ъ▓АэЖаэХШьШАыЛд. ыШРэХЬ Bernardo et al.(2006), Elsayed(2011) ъ╖╕ыжмъ│а Elsayed and Lacor(2013)ьЭА ьЫРьЛмы╢Дыжмъ╕░ьЭШ эШХьГБы│АэЩФьЧР ыФ░ые╕ ыВ┤ы╢А ьЬаыПЩ ы│АэЩФьЧР ыМАэХЬ ьЧ░ъ╡мые╝ ьИШэЦЙэХШьЧм Vortex finderьЭШ ъ╕╕ьЭ┤ы│АэЩФьЧР ыФ░ые╕ ь╢Х ы░йэЦе ьЖНыПД ы░П ьаСьДаы░йэЦе ьЖНыПДьЭШ ы│АэЩФые╝ ы╢ДьДЭэХШьШАыЛд. Dias et al.(2009)ыКФ ьЫРьЛмы╢Дыжмъ╕░ эХШы╢АьЭШ ъ▓╜ъ│Дьб░ъ▒┤ьЧР ыФ░ые╕ ыВ┤ы╢АьЬаыПЩ ы│АэЩФьЧР ъ┤АэХЬ ьИШь╣ШьаБ ьЧ░ъ╡мые╝ эЖ╡эХ┤ ыВ┤ы╢АьЬаыПЩьЧРьДЬ ъ▓╜ъ│Д ьб░ъ▒┤ьЭШ ьдСьЪФьД▒ьЭД эММьХЕэХШъ│а ьЭ┤ые╝ ьЛдэЧШъ│╝ ы╣Дъ╡РэХШьШАыЛд. эХЬэО╕, ь╡Ьъ╖╝ьЧРыКФ Papoulias and Lo(2015)ьЧР ьЭШэХ┤ ыЛдьГБьЬаыПЩ ыкиыН╕ьЭ╕ VOF(Volume of fluid)ые╝ ьЭ┤ьЪйэХЬ ъ│╡ъ╕░-ы╢Дь▓┤ьЭШ ьИШь╣Ш ьЛЬыомыаИьЭ┤ьЕШьЭ┤ ьИШэЦЙыРШьЧИьЬ╝ый░, ъ╖╕ ъ▓░ъ│╝ые╝ ьЛдэЧШъ│╝ ы╣Дъ╡Р ы░П ъ▓АьжЭьЭД эЖ╡эХ┤ ыЛдьГБьЬаыПЩьЭШ ьаБьЪй ъ░АыКеьД▒ьЭД ы│┤ьШАыЛд.
эХЬэО╕, ы╢ДьзД ьЫРьЛм ы╢Дыжмъ╕░ьЭШ ьзСьзДэЪиьЬиьЧР ъ┤АэХЬ ьЧ░ъ╡мыбЬьДЬ Cooper and Alley,(1994)ьЭА ыВ┤ы╢А ьХХыаеы│АэЩФьЩА ьЮЕьЮРьЭШ ь▓┤ыеШ ьЛЬъ░Д ыУ▒ьЭД ьЭ┤ьЪйэХШьЧм ъ╕░ь┤ИьаБьЭ╕ ьЭ┤ыбаьЛЭьЧР ыМАэХ┤ ьЧ░ъ╡мые╝ ьИШэЦЙэХШьШАьЬ╝ый░, Lapple(1951)ьЭА CCD(Classical cyclone design)ыбЬ ы╢ИыжмыКФ ьЛЭьЭД ьаЬьХИэХШьЧм ьЫРьЛм ы╢Дыжмъ╕░ьЭШ ьзСьзДэЪиьЬи ьЧ░ъ╡мьЧР ъ╕░ьдАьЭД ызИыаиэХШьШАьзАызМ ьЫРьЛм ы╢Дыжмъ╕░ьЭШ эШХьГБы│АэЩФьЧР ыФ░ые╕ ьЮЕъ╡мьЖНыПДьЩА ьЬаэЪиэЪМьаДьИШые╝ ъ│аыадэХШьзАыКФ ык╗эХШьШАыЛд. ьЭ┤ ым╕ьаЬые╝ эХ┤ъ▓░эХШъ╕░ ьЬДэХ┤ Dirgo and Leith(1985)ьЭА ьЮЕьЮРэБмъ╕░ ы░П ьЖНыПДы│Д ьЛдэЧШьЭД эЖ╡эХ┤ ьЭ┤ыбаьЛЭьЭД ыПДь╢ЬэХШьЧм CCDьЭШ ым╕ьаЬьаРьЭД ы│┤ьХИэХШьШАыЛд. ьЭ┤ьЩ╕ьЧРыПД ьЮЕьЮРэБмъ╕░ ы░П ьЖНыПДьЧР ыФ░ые╕ ьзСьзД эЪиьЬиьЭШ ьЛдэЧШъ╕░ы░ШьЭШ ьЭ┤ыбаьЛЭьЧР ъ┤АэХЬ ызОьЭА ьДаэЦЙьЧ░ъ╡мыУд(Barth, 1956; Leith and Licht, 1972; Dietz, 1981; Li and Wang, 1989; Iozia and Leith, 1990)ьЭ┤ ьЮИьЬ╝ыВШ, ьвЕэХйэХ┤ ы│┤ый┤ ъ╕░ ьаЬьХИыРЬ ьЭ┤ыбаьЛЭьЬ╝ыбЬыКФ ьЫРьЛмы╢Дыжмъ╕░ эШХьГБьЧР ыФ░ые╕ ьзСьзД эЪиьЬиьЭШ ь╢ФьаХьЧР эХЬъ│Дъ░А ьЮИьЦ┤ ы│┤ьЭ╕ыЛд.
ы│╕ ьЧ░ъ╡мьЧРьДЬыКФ ьЫРьЛм ы╢Дыжмъ╕░ ыВ┤ы╢АьЭШ эЪМьаДьЬаыПЩьЧР ыМАэХШьЧм ьаДьВ░ьЬаь▓┤ьЧнэХЩ(Computational fluid dynmics, CFD)ьЭД ьЭ┤ьЪйэХЬ ьИШь╣Ш ьЛЬыомыаИьЭ┤ьЕШьЭД ьИШэЦЙэХШьЧм ъ╖╕ ъ▓░ъ│╝ые╝ ы░ФэГХьЬ╝ыбЬ ьЮЕьЮРэБмъ╕░ьЧР ыФ░ые╕ ьзСьзДэЪиьЬиьЭД ь╢ФьаХэХ┤ ы│┤ьХШыЛд. ыи╝ьаА, CFD ьЛЬыомыаИьЭ┤ьЕШьЭА ьГБьЪй ьЖМэФДэК╕ьЫиьЦ┤ьЭ╕ STAR-CCM+ьЭД ьЭ┤ьЪйэХШьЧм ьЫРьЛм ы╢Дыжмъ╕░ ыВ┤ы╢АьЭШ ыЛиьГБыеШьЧР ъ┤АэХЬ ьЬаыПЩэХ┤ьДЭьЭД ьИШэЦЙэХШьШАьЬ╝ый░, ьЛЬыомыаИьЭ┤ьЕШ ъ▓░ъ│╝ые╝ ьЛдэЧШ(Boysan et al., 1983) ы░П эГА ьИШь╣Ш ьЛЬыомыаИьЭ┤ьЕШ(Slack et al., 2000)ъ│╝ ы╣Дъ╡Р ъ▓АэЖаэХШьЧм эГАыЛ╣ьД▒ьЭД эЩХьЭ╕эХШьШАыЛд. ьЭ┤эЫД ъ╖╕ ъ▓░ъ│╝ые╝ ы░ФэГХьЬ╝ыбЬ ъ│╡ъ╕░-ы╢Дь▓┤ ьЬаыПЩьЭШ ыЛиы░йэЦе(1-way) ьЧ░ьД▒ ьЛЬыомыаИьЭ┤ьЕШьЭД эЖ╡эХЬ ьзСьзДэЪиьЬиьЭД ьВ░ь╢ЬэХШьЧм ьДаэЦЙьЧ░ъ╡мьЮР(Dirgo and Leith, 1985)ьЭШ ьЛдэЧШъ░Т ы░П ъ╕░ ьаЬьХИыРЬ ьЭ┤ыбаъ░ТыУдъ│╝ ы╣Дъ╡РтЛЕъ▓АьжЭэХШьШАыЛд.
ы│╕ ьЧ░ъ╡мьЧРьДЬыКФ эХДэД░ызБ ьб░ьЮСьЧР ьЭШэХЬ Grid scale(GS)ьЭШ ы╣ДьХХь╢ХьД▒ ьЬаыПЩьЭШ ьзАы░░ ы░йьаХьЛЭьЭА ьЧ░ьЖНы░йьаХьЛЭъ│╝ Navier-Stokes ы░йьаХьЛЭьЭ┤ый░, ъ░Бъ░Б ыЛдьЭМъ│╝ ъ░ЩьЭ┤ эСЬэШДыРЬыЛд.
ьЧмъ╕░ьДЬ u i u j p S i j
ы╢Дь▓┤-ъ╕░ь▓┤ эШ╝ьГБыеШ ьЛЬыомыаИьЭ┤ьЕШьЧРьДЬыКФ ыЭ╝ъ╖╕ыЮСьзАьХИ ъ┤АьаРьЭШ LPT(Lagrangian particle tracking) ы░йы▓ХьЭД ьВмьЪйэХШьШАъ│а ъ░Б ьЮЕьЮРьЧР ьЮСьЪйэХШыКФ эЮШьЭД ьЛЭ (3)ъ│╝ ъ░ЩьЭ┤ ыВШэГАыВ┤ьЧИыЛд.
ьЧмъ╕░ьДЬ FdыКФ эХныае, FpыКФ ьХХыае ъ╡мы░░ыае, FvmыКФ ъ░АьГБ ьзИыЯЙыае, FgыКФ ьдСыае ъ╖╕ыжмъ│а FuыКФ ьВмьЪйьЮР ьаХьЭШьЧР ьЭШэХЬ эЮШьЭД ыВШэГАыВ┤ый░ ы│╕ ьЧ░ъ╡мьЧРьДЬыКФ Fvmъ│╝ FuьЭА ъ│аыадыРШьзА ьХКьХШыЛд.
ыи╝ьаА ъ░Б ьЮЕьЮРьЧР ьЮСьЪйэХШыКФ эЮШ ьдС эХныаеьЧР ыМАэХ┤ эСЬъ╕░эХШый┤ ьХДыЮШ ьЛЭъ│╝ ъ░ЩьЭ┤ ыВШэГАыВ╝ ьИШ ьЮИыЛд.
ьЧмъ╕░ьДЬ CdыКФ ьЮЕьЮРьЭШ эХныаеъ│ДьИШ, ╧БcыКФ ъ╕░ь▓┤ьЭШ ы░АыПД, ApыКФ ьЮЕьЮРьЭШ ыЛиый┤ьаБ, vcыКФ ъ╕░ь▓┤ьЭШ ьЖНыПД, vpыКФ ьЮЕьЮРьЭШ ьЖНыПД, vsыКФ ьЮЕьЮРьЭШ Slip ьЖНыПДые╝ ыВШэГАыВ╕ыЛд. ьЭ┤ ыХМ эХныаеъ│ДьИШыКФ ъ╡мэШХьЭШ ьЮЕьЮРые╝ ъ│аыадэХа ьИШ ьЮИыКФ Schiller and NaumannьЭШ ьГБъ┤АьЛЭьЭД ьЭ┤ьЪйэХШьЧм ъ│ДьИШ ъ░ТьЭ┤ ы│┤ьаХыРШый░ ыЛдьЭМъ│╝ ъ░ЩьЭ┤ ыВШэГАыВ╕ыЛд.
ыЛи, ьЮЕьЮРьЭШ ыаИьЭ┤ыЖАьжИ ьИШ RepыКФ ыЛдьЭМъ│╝ ъ░ЩьЭ┤ ьаХьЭШыРЬыЛд.
ыЛдьЭМьЬ╝ыбЬ ьЮЕьЮРьЧР ьЮСьЪйэХШыКФ ьХХыаеьЧР ьЭШэХЬ эЮШъ│╝ ьдСыаеьЭД ыВШэГАыВ┤ый┤ ыЛдьЭМъ│╝ ъ░ЩыЛд.
ьЧмъ╕░ьДЬ VpыКФ ьЮЕьЮРьЭШ ы╢АэФ╝, pstaticыКФ ъ╕░ь▓┤ьЭШ ьаХьХХыае, mpыКФ ьЮЕьЮРьЭШ ы░АыПДые╝ ыВШэГАыВ╕ыЛд.
ы╢Дь▓┤ыКФ ъ╖аьЭ╝эХЬ эБмъ╕░ьЭШ ъ╡мэШХьЭШ ьЮЕьЮРыбЬ ъ░АьаХэХШьШАьЬ╝ый░ ьЬаь▓┤ьЧР ьЭШэХЬ ы╢Дь▓┤ьЪ┤ыПЩьЭД ьЮмэШДэХШъ╕░ ьЬДэХ┤ ьЬаь▓┤ьЩА ы╢Дь▓┤ ы░П ы╢Дь▓┤ьЩА ы╢Дь▓┤ьЭШ ьГБэШ╕ ьЮСьЪйьЭ┤ ъ│аыадыРШьзА ьХКыКФ 1-way ьЧ░ьД▒ ьЛЬыомыаИьЭ┤ьЕШьЭД ьИШэЦЙэХШьШАыЛд. 1-way ьЛЬыомыаИьЭ┤ьЕШьЭШ ъ▓╜ьЪ░, ьЬаь▓┤ьЩА ы╢Дь▓┤ьЭШ ьГБэШ╕ьЮСьЪйьЭ┤ ъ│аыадыРШьзА ьХКьХД ьГБыМАьаБьЬ╝ыбЬ 2-way ьЛЬыомыаИьЭ┤ьЕШьЧР ы╣ДэХ┤ ъ│ДьВ░ ьЛЬъ░ДьЧР ьЮеьаРьЭ┤ ьЮИьзАызМ, ы╢Дь▓┤ьЭШ эБмъ╕░ъ░А ьЬаыПЩьЧР ьШБэЦеьЭД ьдДызМэБ╝ эБ┤ ъ▓╜ьЪ░ ъ│ДьВ░ ьаХэЩХыПДыКФ ьГБыМАьаБьЬ╝ыбЬ ыВоыЛд. эХШьзАызМ ы│╕ ьЧ░ъ╡мьЧРьДЬыКФ LPT ы░йы▓ХьЭШ ьаБьЪйьЭД эЖ╡эХЬ ьИШь╣Ш ьЛЬыомыаИьЭ┤ьЕШьЭШ ьаХэЩХыПД эЦеьГБьЧР ьХЮьДЬ ьаБьЪйъ░АыКеьД▒ьЭД эЩХьЭ╕эХШъ╕░ ьЬДэХ┤ ьГБыМАьаБьЬ╝ыбЬ ъ│ДьВ░ ьЛЬъ░ДьЧР ьЮеьаРьЭД ъ░АьзАыКФ 1-way ьЧ░ьД▒ ъ╕░ы▓ХьЭД ьаБьЪйэХШьШАыЛд.
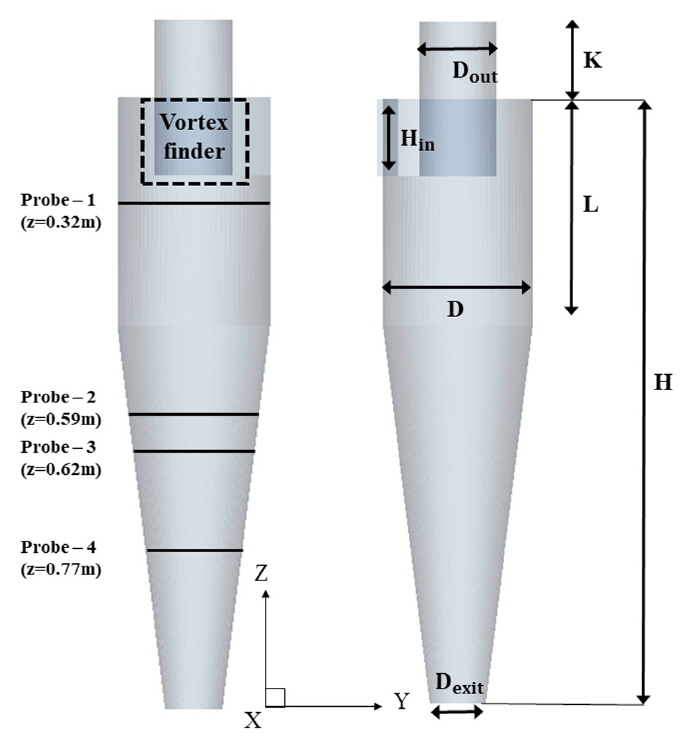
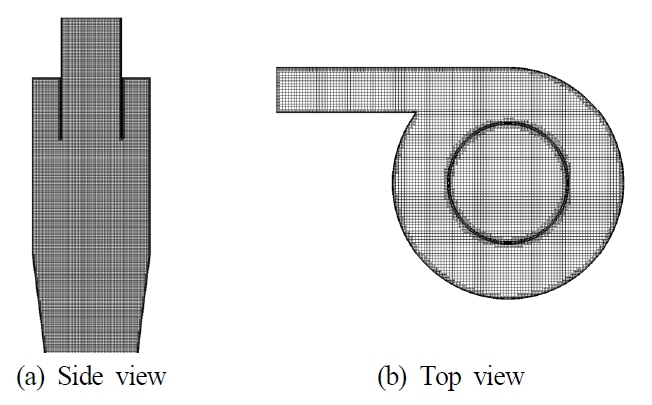
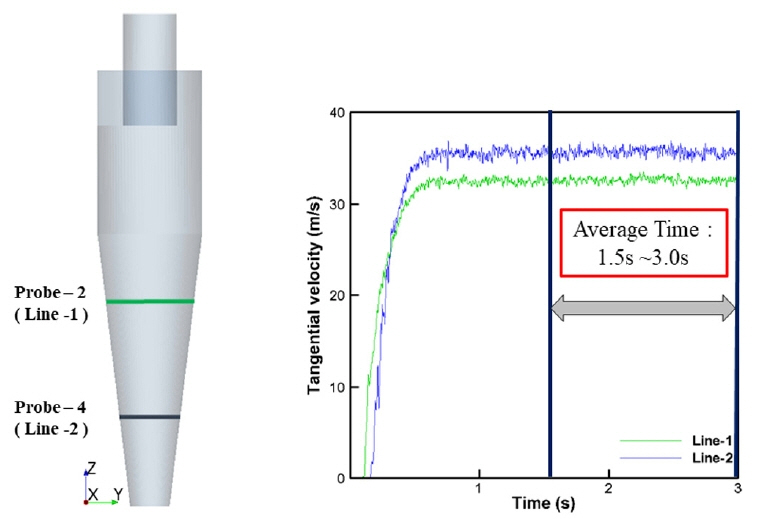
CFD ьЛЬыомыаИьЭ┤ьЕШьЭД ьЬДэХЬ эШХьГБьЭА Fig. 1ъ│╝ ъ░ЩьЭА ьЫРь╢ФэШХ ьЫРьЛмы╢Дыжмъ╕░ьЭ┤ый░ ьГБьД╕эХЬ ьаЬьЫРьЭА Table 1ьЧР ьЪФьХ╜эХШьШАыЛд. ыЛи, Fig. 1(a)ьЭШ Probes 1~4ыКФ ь╢Хы░йэЦе ьЖНыПДьЩА ьаСьДаы░йэЦе ьЖНыПДые╝ ъ│Дь╕бэХШъ╕░ ьЬДэХЬ ьЬДь╣Шые╝ ъ░Бъ░Б ыВШэГАыВ╕ыЛд. ьЛЬыомыаИьЭ┤ьЕШьЭД ьЬДэХЬ ъ▓йьЮРъ│ДыКФ STAR-CCM+ьЧР ьаЬъ│╡эХШыКФ ьЮРыПЩъ▓йьЮР ьГЭьД▒ ы░йы▓ХьЭД ьЭ┤ьЪйэХШьЧм ьГЭьД▒эХШьШАьЬ╝ый░ ы▓╜ый┤ьЧРьДЬ ы▓ХьДаы░йэЦеьЬ╝ыбЬьЭШ ь╡ЬьЖМ ъ▓йьЮР ьВмьЭ┤ьжИыКФ 5├Ч10-4mьЭ┤ъ│а, ъ▓йьЮР ьИШыа┤ьД▒ эЕМьКдэК╕ые╝ эЖ╡эХ┤ ь╡ЬьвЕьаБьЬ╝ыбЬ Fig. 2ьЧР ыВШэГАыВ╕ ы░ФьЩА ъ░ЩьЭ┤ ь┤Э 300ызМъ░ЬьЭШ ъ▓йьЮРые╝ ьВмьЪйэХШьШАыЛд.
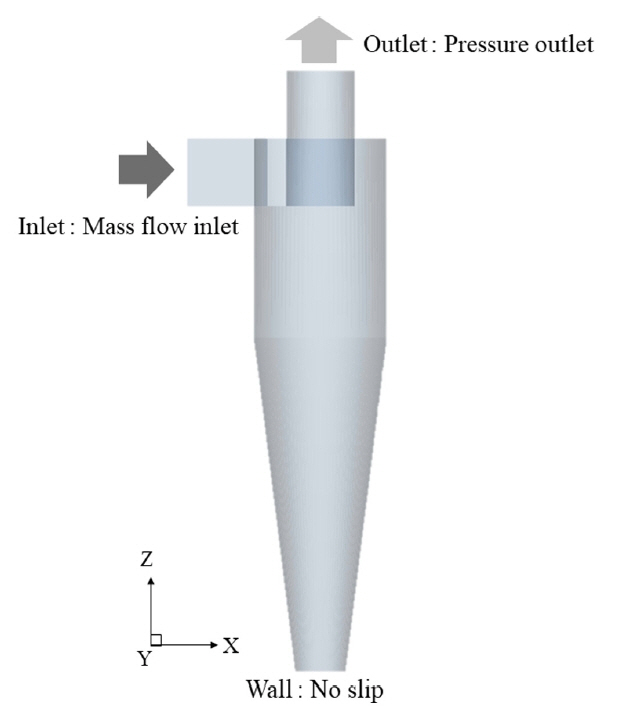
ьЮЕъ╡мьЧРьДЬьЭШ ьЬаьЮЕыРШыКФ ъ│╡ъ╕░ ы░П ы╢ДьзДьЭШ ьзИыЯЙ ьЬаыЯЙьЭА Table 2ьЩА ъ░ЩьЭ┤ ыЛиьГБьЬаыПЩьЭШ ъ▓╜ьЪ░ 0.098kg/sьЭШ ъ│╡ъ╕░ые╝, ыЛдьГБьЬаыПЩьЭШ ъ▓╜ьЪ░ 0.098kg/sьЭШ ъ│╡ъ╕░ьЩА 0.002kg/sьЭШ ы╢ДьзДьЭ┤ ъ│аыадыРШьЧИыЛд. ьГБы╢АьЬаь╢Ьъ╡мьЭШ ъ▓╜ьЪ░ ыМАъ╕░ьХХ ьб░ъ▒┤ьЭД ьаБьЪйэХШьШАьЬ╝ый░, эХШы╢АьЬаь╢Ьъ╡мьЭШ ъ▓╜ьЪ░ ьЛдэЧШьЧРьДЬыКФ ы╢ДьзДьЭД ьИШьзСэХШъ╕░ ьЬДэХЬ эГ▒эБмъ░А ьб┤ьЮмэХШьзАызМ ы│╕ ьЧ░ъ╡мьЧРьДЬыКФ Dias et al.(2009)ьЭШ ьДаэЦЙьЧ░ъ╡мые╝ ь░╕ъ│аэХШьЧм ызЙэШАьЮИыКФ ы▓╜ьЬ╝ыбЬ ь▓ШыжмэХШьШАыЛд. ьЛЬыомыаИьЭ┤ьЕШьЭШ ъ▓╜ъ│Дьб░ъ▒┤ьЭА Fig. 3ьЧР ыВШэГАыВ┤ьЧИыЛд. ьЬаьЮЕъ▓╜ъ│ДыбЬы╢АэД░ ьЬаьЮЕыРЬ ьЬаь▓┤ыКФ ьЫРьЛмы╢Дыжмъ╕░ьЭШ эШХьГБьЭД ыФ░ыЭ╝ ьаДыЛиьЖНыПДьЧР ьЭШэХ┤ ьДаэЪМэХШъ▓М ыРЬыЛд.
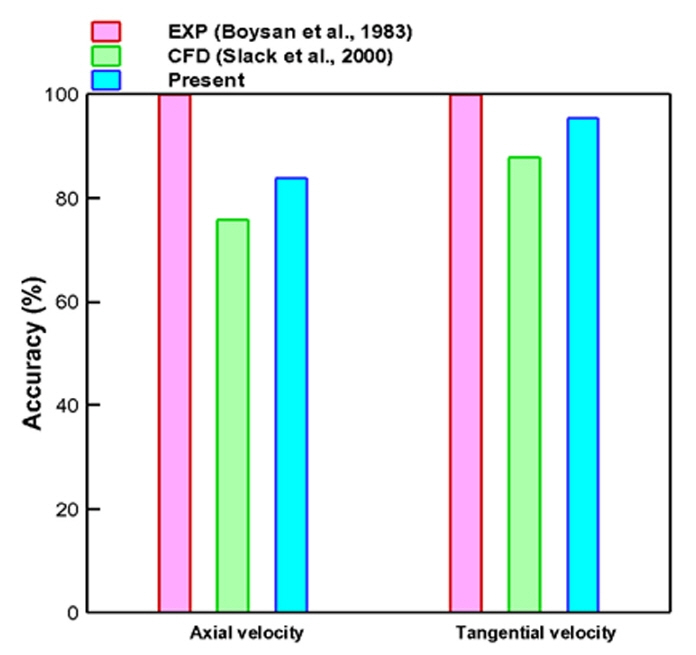
ьИШь╣Ш ьЛЬыомыаИьЭ┤ьЕШьЭШ ьаБьЪй ъ░АыКеьД▒ьЭД ъ▓АьжЭэХШъ╕░ ьЬДэХЬ ыЛиьГБыеШьЧР ыМАэХЬ ьИШь╣Ш ьЛЬыомыаИьЭ┤ьЕШьЭД ьИШэЦЙэХШьШАьЬ╝ый░, ьаДьИаэХЬ 4ъ││ьЭШ ь╕бьаХьЬДь╣ШьЧРьДЬ ь╢Хы░йэЦеъ│╝ ьаСьДаы░йэЦе ьЖНыПДые╝ Slack et al.(2000)ьЭШ CFD ьЛЬыомыаИьЭ┤ьЕШ ъ▓░ъ│╝ ы░П Boysan et al.(1983)ьЭШ ьЛдэЧШъ▓░ъ│╝ьЩА ьГБэШ╕ ы╣Дъ╡РэХШьШАыЛд.
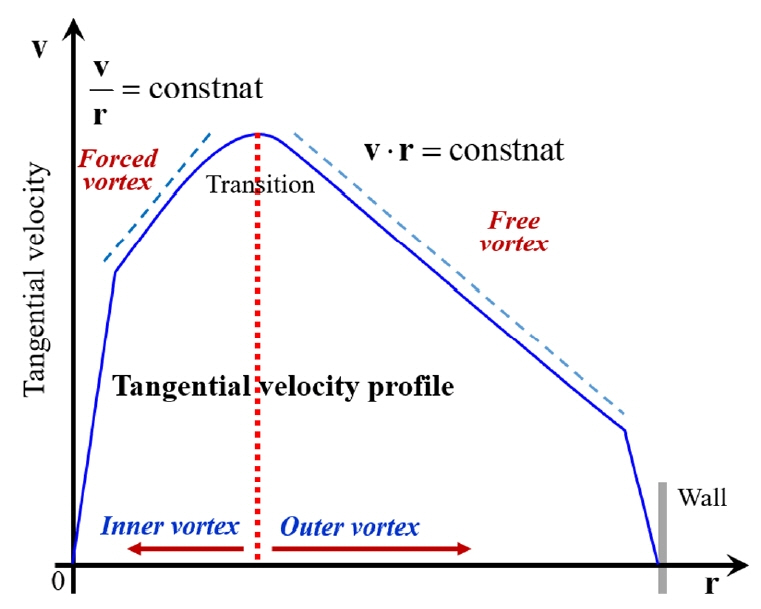
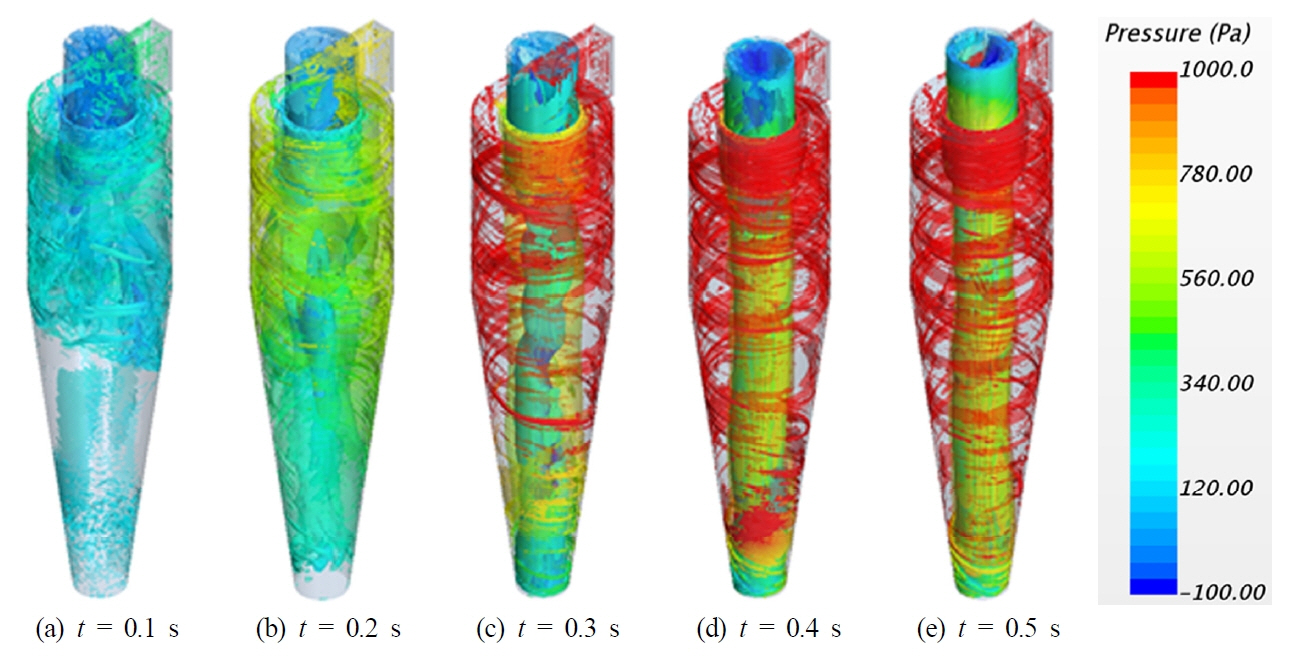
Fig. 4ьЧРыКФ ьЫРьЛмы╢Дыжмъ╕░ ыВ┤ы╢АьЧРьДЬ эШХьД▒ыРШыКФ эЪМьаДьЬаыПЩьЭШ ьЛЬъ░ДьЧР ыФ░ые╕ ы░ЬыЛмъ│╝ьаХьЭД ьХХыаеъ│╝ эХиъ╗Ш ыВШэГАыВ╕ыЛд. ьЮЕъ╡мьЧР эИмьЧмыРЬ ьЬаыПЩьЭА ьЫРьЛмы╢Дыжмъ╕░ ыВ┤ьЧРьДЬ ьГБы╢АьЭШ ьЩ╕ы▓╜ьЭД ыФ░ыЭ╝ эЪМьаДыеШыбЬ ы░ЬыЛмэХШый░ t=0.2s ы╢Аъ╖╝ьЧРыКФ ьаАый┤ьЧР ыПДыЛмэХШъ▓М ыРЬыЛд. ьЭ┤эЫД t=0.3s ьЭ┤эЫДьЧРыКФ эЪМьаДьЬаыПЩьЭШ ьШБэЦеьЬ╝ыбЬ ьЭ╕эХ┤ ьЫРьЛмы╢Дыжмъ╕░ьЭШ ьдСьЛмы╢АьЧРыКФ ьХХыаеьЭ┤ ьГБыМАьаБьЬ╝ыбЬ ыВоьЭА ьШБьЧньЭ┤ эШХьД▒ыРШъ│а ьЮИьЭМьЭД ьХМ ьИШ ьЮИьЬ╝ый░, ьЭ┤ ьШБьЧньЧРьДЬыКФ ьЬаыПЩьЭ┤ эЪМьаД ьГБьК╣эХШьЧм ьГБы╢АьЭШ Vortex finderые╝ ьзАыВШ ь╢Ьъ╡мыбЬ ы╣аьа╕ыВШъ░АыКФ ъ▓ГьЭД эЩХьЭ╕эХа ьИШ ьЮИыЛд. ьЭ╝ы░ШьаБьЬ╝ыбЬ ьЫРьЛмы╢Дыжмъ╕░ ыВ┤ы╢АьЧРьДЬ ьГЭьД▒ ы░П ы░ЬыЛмыРШыКФ эЪМьаДьЬаыПЩьЭА Fig. 5ьЧР ыВШэГАыВ╕ ъ▓Гь▓ШыЯ╝ ьаСьДаы░йэЦеьЭШ ьЖНыПД эФДыбЬэММьЭ╝ьЭД эЖ╡эХ┤ ыВ┤ы╢А(Inner)ьЩА ьЩ╕ы╢А(Outer)ьЭШ ьЩАыеШьШБьЧн(Vortex region)ьЬ╝ыбЬ ъ╡мы╢ДыРШыКФ эК╣ьД▒ьЭД ы│┤ьЭ┤ыКФ ъ▓ГьЬ╝ыбЬ ьХМыадьа╕ ьЮИыКФыН░(Wang, 2004), эК╣эЮИ ьдСьЛмы╢АьЧРьДЬьЭШ ыВ┤ы╢А ьЩАыеШьШБьЧньЭА Fig. 4ьЧРьДЬьЩА ъ░ЩьЭ┤ ьХХыае ьаАэХШыбЬ ьЭ╕эХ┤ ъ╕░ьЭ╕ыРЬыЛдыКФ ъ▓ГьЭД ьХМ ьИШ ьЮИыЛд.
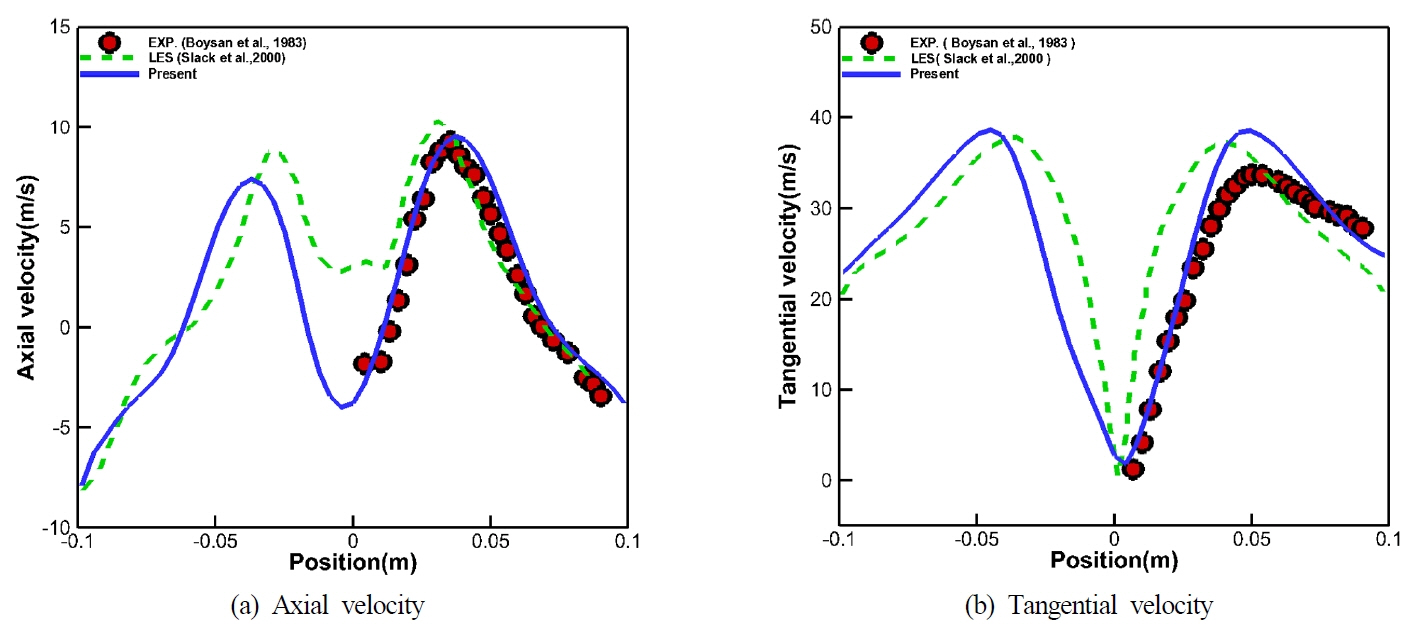
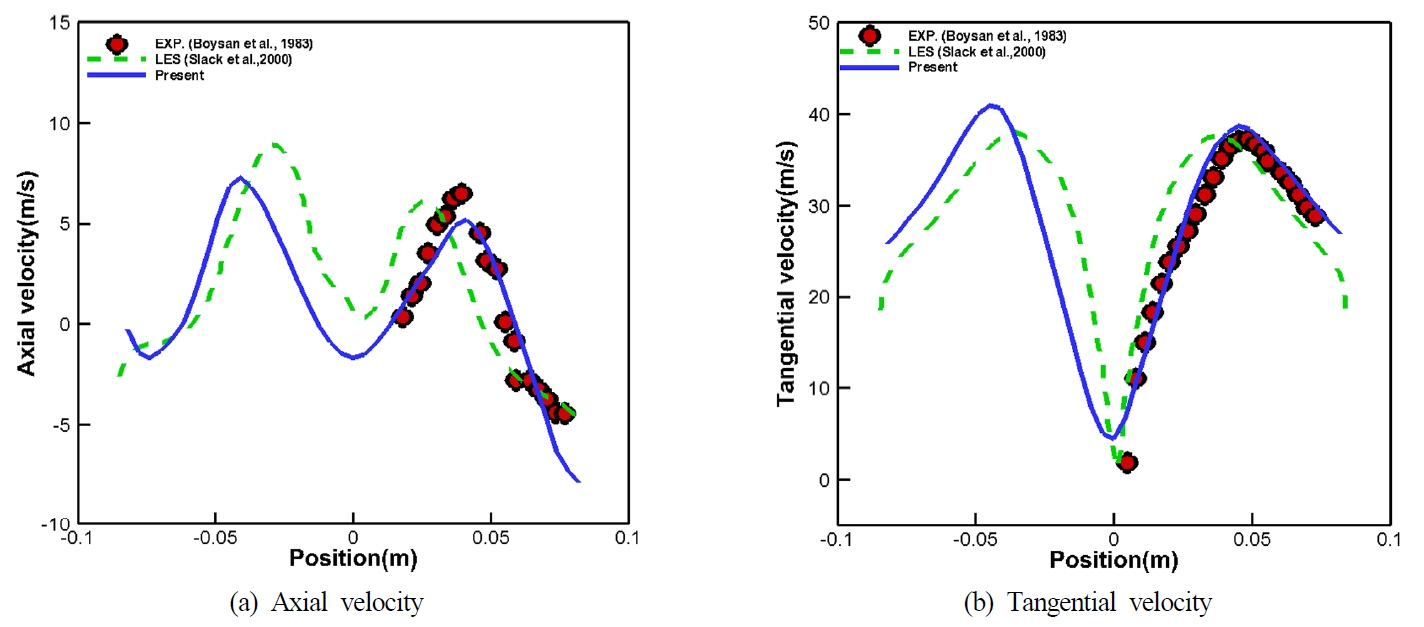
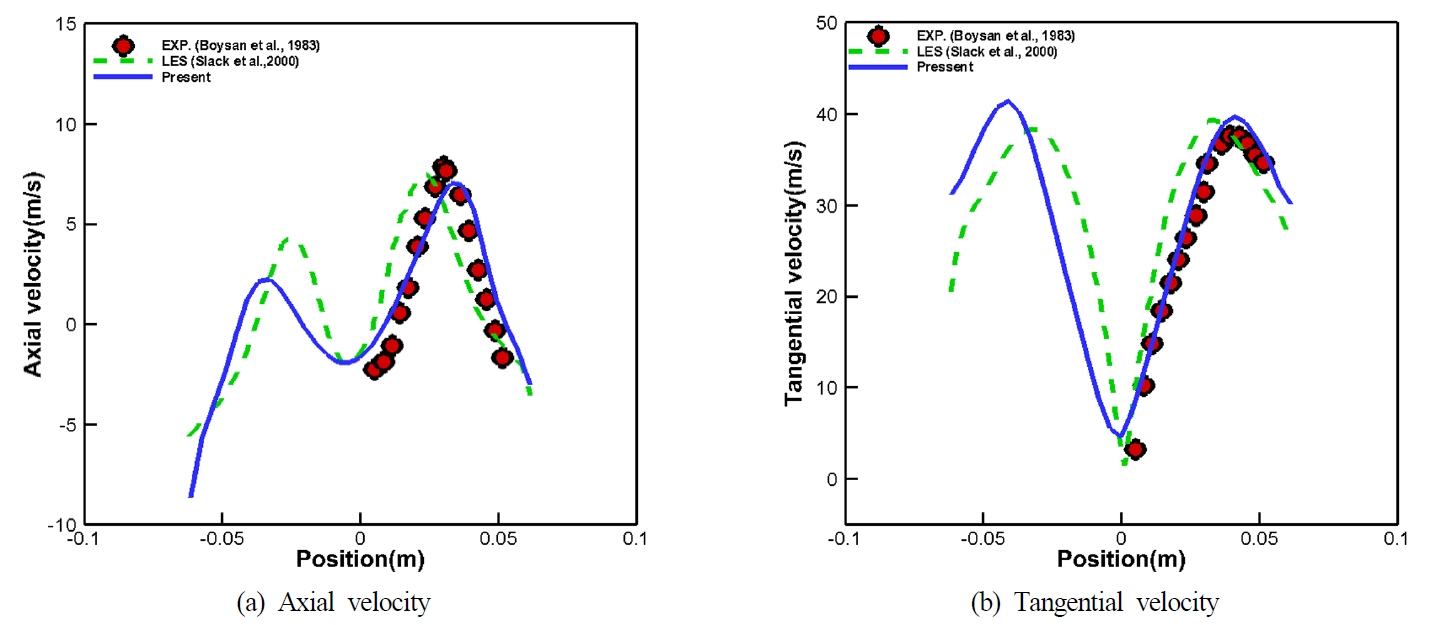
ыЛдьЭМьЬ╝ыбЬ, ы│╕ CFD ьЛЬыомыаИьЭ┤ьЕШьЭШ ъ▓░ъ│╝ ъ▓АьжЭьЭД ьЬДэХ┤, Fig. 6ьЧР ы│┤ьЭ┤ыКФ ы░ФьЩА ъ░ЩьЭ┤ ьаСьДаы░йэЦе ьЖНыПДы╢ДэПмьЭШ ьЛЬъ│ДьЧ┤ ъ▓░ъ│╝ыбЬы╢АэД░ ьЬаыПЩьЮеьЭ┤ ьХИьаХэЩФыРЬ t=1.5s~3.0sыПЩьХИ ь╢Хы░йэЦе ы░П ьаСьДаы░йэЦеьЭШ ьЖНыПДьД▒ы╢ДьЭД ъ░Бъ░Б эПЙъ╖аэХШьЧм ьЛдэЧШ ы░П эГА CFD ьЛЬыомыаИьЭ┤ьЕШ ъ▓░ъ│╝ьЩА ы╣Дъ╡РэХШьШАыЛд. Figs. 7-10ьЧРьДЬ эЩХьЭ╕эХа ьИШ ьЮИыУпьЭ┤, ьаСьДаы░йэЦе ьЖНыПДьД▒ы╢ДьЭШ ы╢ДэПмы┐РызМьЭ┤ ьХДыЛИыЭ╝ ь╢Хы░йэЦе ьЖНыПДьД▒ы╢ДьЭШ ы╢ДэПмьЧРьДЬыПД ьаДьИаэХЬ ыВ┤ы╢А ы░П ьЩ╕ы╢АьЭШ ьЩАыеШьШБьЧньЭ┤ ыЪЬыа╖ьЭ┤ ъ╡мы╢ДыРШьЦ┤ ыВШэГАыВШый░ ыкиыУа ь╕бьаХьЬДь╣ШьЧРьДЬ ьЛдэЧШъ░Тъ│╝ ьаХьД▒ьаБьЬ╝ыбЬ ьЮШ ьЭ╝ь╣ШэХШъ│а ьЮИьЭМьЭД ьХМ ьИШ ьЮИыЛд. ы│┤ыЛд ьаХыЯЙьаБьЭ╕ ы╣Дъ╡Рые╝ ьЬДэХШьЧм ъ░Б ьЖНыПД ьД▒ы╢ДьЭШ ьЛдэЧШъ▓░ъ│╝ ыМАы╣Д ьЛЬыомыаИьЭ┤ьЕШ ъ▓░ъ│╝ьЭШ ьаХэЩХыПДые╝ ьЛЭ (10)ые╝ эЖ╡эХ┤ ьВ░ь╢ЬэХШьЧм Fig. 11ьЧР ыВШэГАыВ╕ыЛд. ъ▓░ъ│╝ьаБьЬ╝ыбЬ ы│╕ ьЛЬыомыаИьЭ┤ьЕШ ы░П эГА ьЛЬыомыаИьЭ┤ьЕШ ъ▓░ъ│╝(Slack et al., 2000)ыКФ ьЛдэЧШьЧР ы╣ДэХШьЧм ъ░Бъ░Б 96.4%ьЩА 85.8%ьЭШ эПЙъ╖аьаБьЭ╕ ьГБыМАьШдь░иые╝ ы│┤ьЭ┤ыКФ ъ▓ГьЬ╝ыбЬ эЩХьЭ╕ыРШьЧИыЛд. ьЦС ьЛЬыомыаИьЭ┤ьЕШьЭШ эБмыВШ эБ░ ь░иьЭ┤ьаРьЭ┤ыЭ╝ъ│а эХЬыЛдый┤, ыВЬыеШыкиыН╕ыбЬьНи ыПЩьЭ╝эХЬ Large eddy simulation(LES) ыкиыН╕ьЭД ьВмьЪйэХШьШАьЬ╝ыВШ SGSьЭШ Eddyые╝ ъ╡мэШДэХШъ╕░ ьЬДэХ┤ Slack et al.(2000)ьЭШ ъ▓╜ьЪ░ыКФ Renormalization groupьЭШ Subgrid scale(RNG-SGS) ыкиыН╕(Yakhot et al., 1989)ьЭД ьВмьЪйэХЬ ьаРъ│╝, ъ▓йьЮРьЛЬьКдэЕЬьЭШ эЪиьЬиьД▒ьЭД ъ│аыадэЦИыЛдыКФ ьаР ыУ▒ьЭД ыУд ьИШ ьЮИыЛд. ьЭ┤ые╝ эЖ╡эХ┤ ы│╕ ьЛЬым╝ыаИьЭ┤ьЕШьЭШ ъ▓░ъ│╝ъ░А ьЛдэЧШъ░ТьЧР ы│┤ыЛд ъ╖╝ьаСэХЬ ъ▓░ъ│╝ые╝ ы│┤ьЭ╕ыЛдыКФ ъ▓ГьЭД ьЭШып╕эХЬыЛдъ│а эХа ьИШ ьЮИыЛд.
ьЧмъ╕░ьДЬ vvmыКФ ъ░Б ьЖНыПДьД▒ы╢ДьЭШ ьЛЬыомыаИьЭ┤ьЕШ ъ▓░ъ│╝, vexpыКФ ъ░Б ьЖНыПДьД▒ы╢ДьЭШ ьЛдэЧШъ▓░ъ│╝ые╝ ыВШэГАыВ╕ыЛд.
ьЫРьЛмы╢Дыжмъ╕░ьЭШ эЪиьЬиьЭД ь╢ФьаХэХШъ╕░ ьЬДэХШьЧм ъ│╡ъ╕░-ы╢Дь▓┤ьЭШ ьЬаыПЩьЭА Eulerian-LagrangianьЭШ ыЛиы░йэЦе(1-way) ьЧ░ьД▒ эХ┤ьДЭьЬ╝ыбЬ ьИШэЦЙэХШьШАьЬ╝ый░ Lagrangian particleьЭД ьЭ┤ьЪйэХШьЧм ъ╡м эШХьГБьЭШ ы╢Дь▓┤ые╝ ъ╡мэШДэХШьШАыЛд. ы╢ДыжмэЪиьЬиьЭА ьЬаьЮЕыРЬ ы╢Дь▓┤ьЭШ ьЦСъ│╝ ьЬаь╢ЬыРЬ ы╢Дь▓┤ьЭШ ьЦСьЭД эЖ╡эХ┤ ьЛЭ (11)ъ│╝ ъ░ЩьЭ┤ ьВ░ь╢ЬэХШьШАъ│а ьЭ┤ые╝ ьЛдэЧШъ░Тъ│╝ ы╣Дъ╡РэХШьШАыЛд. ьЭ┤ ыХМ ы╢Дь▓┤ьЮЕьЮРьЭШ эБмъ╕░ыКФ ъ░Бъ░Б 1, 3, 5уОЫые╝ ъ│аыадэХШьШАьЬ╝ый░, ьЬаь╢Ь ъ▓╜ъ│ДьЧРьДЬ ьЬаь╢ЬыРЬ ьЮЕьЮРьИШые╝ ь╕бьаХэХШьЧм ы╢ДыжмэЪиьЬиьЭД ьВ░ь╢ЬэХШьШАыЛд.
ьЧмъ╕░ьДЬ ╬╖ыКФ ы╢ДыжмэЪиьЬи, moutletьЭА Gas outletьЬ╝ыбЬ ы╣аьа╕ыВШъ░Д ьЮЕьЮРьИШ ъ╖╕ыжмъ│а minletьЭА ьЫРьЛмы╢Дыжмъ╕░ ьЮЕъ╡мыбЬ эИмьЧмыРЬ ьЮЕьЮРьИШые╝ ъ░Бъ░Б ыВШэГАыВ╕ыЛд.
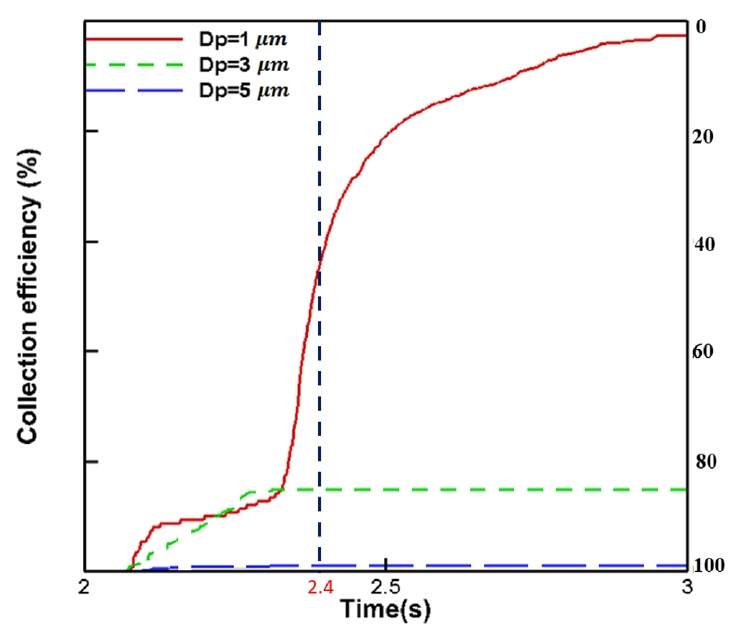
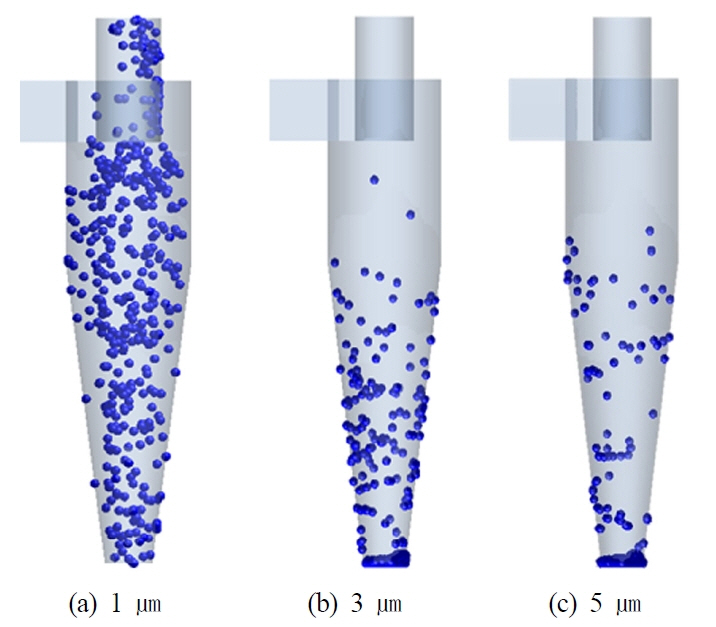
Fig. 12ыКФ ьЛЬъ░ДьЧР ыФ░ые╕ ьЮЕьЮРы│Д ы╢ДыжмэЪиьЬиьЭШ ы│АэЩФ эК╣ьД▒ьЭД ыВШэГАыВ┤ый░, ьЮЕьЮРэБмъ╕░ьЧР ыФ░ые╕ ъ▒░ыПЩьЭД эЩХьЭ╕эХШъ╕░ ьЬДэХ┤ Vortex finderьЧР ьЭШэХЬ 1ь░и ы╢Дыжмъ░А ыБЭыВЬ ьЛЬьаРьЭ╕ t=2.4sьЧРьДЬ ьЮЕьЮРы│Д ъ▒░ыПЩьЭД ъ░АьЛЬэЩФэХШьЧм Fig. 13ьЧР ыВШэГАыВ╕ыЛд. ьЛЬъ░ДьЧР ыФ░ыЭ╝ ьЮЕьЮРы│Д ы╢Дыжм эК╣ьД▒ьЭ┤ ыкЕэЩХэЮИ ъ╡мы╢ДыРШый░, ьГБыМАьаБьЬ╝ыбЬ ьЮЕьЮРьЭШ эБмъ╕░ъ░А ъ░АьЮе ьЮСьЭА 1уОЫьЭШ ъ▓╜ьЪ░ t=2.1s ы╢Аъ╖╝ьЧРьДЬ ьЮЕъ╡мыбЬы╢АэД░ эИмьЧмыРЬ ьЮЕьЮР ьдС ьЭ╝ы╢Аъ░А ьЭ╝ь░иьаБьЬ╝ыбЬ Vortex finderыбЬ ы╣аьа╕ыВШъ░Аъ│а ыВШыи╕ьзАыКФ ьЫРьЛмы╢Дыжмъ╕░ ыВ┤ьЧРьДЬ ьХ╜ 0.3ь┤Иъ░ДьЭШ ь▓┤ыеШьЛЬъ░ДьЭД ъ░АьзД ыТд ыВ┤ы╢А ьЩАыеШьШБьЧньЭД эЖ╡эХ┤ ьГБьК╣ эЪМьаДьЭД эХШый░ ъ▒░ьЭШ ыкиыУа ьЮЕьЮРыУдьЭ┤ Vortex finderые╝ ьзАыВШ ь╢Ьъ╡мыбЬ ы╣аьа╕ыВШъ░АыКФ ъ▓ГьЭД эЩХьЭ╕эХШьШАыЛд. ы░Шый┤ 3уОЫьЩА 5уОЫьЭШ ъ▓╜ьЪ░ эИмьЧмыРЬ ьЮЕьЮРыУдьЭ┤ t=2.5s ьЭ┤эЫДьЧРыКФ Vortex finderыбЬ ы╣аьа╕ыВШъ░АьзА ык╗эХШъ│а ьЫРьЛмы╢Дыжмъ╕░ ыВ┤ьЧРьДЬ ь▓┤ыеШэХШыКФ ъ▓ГьЭД эЩХьЭ╕эХШьШАыЛд.
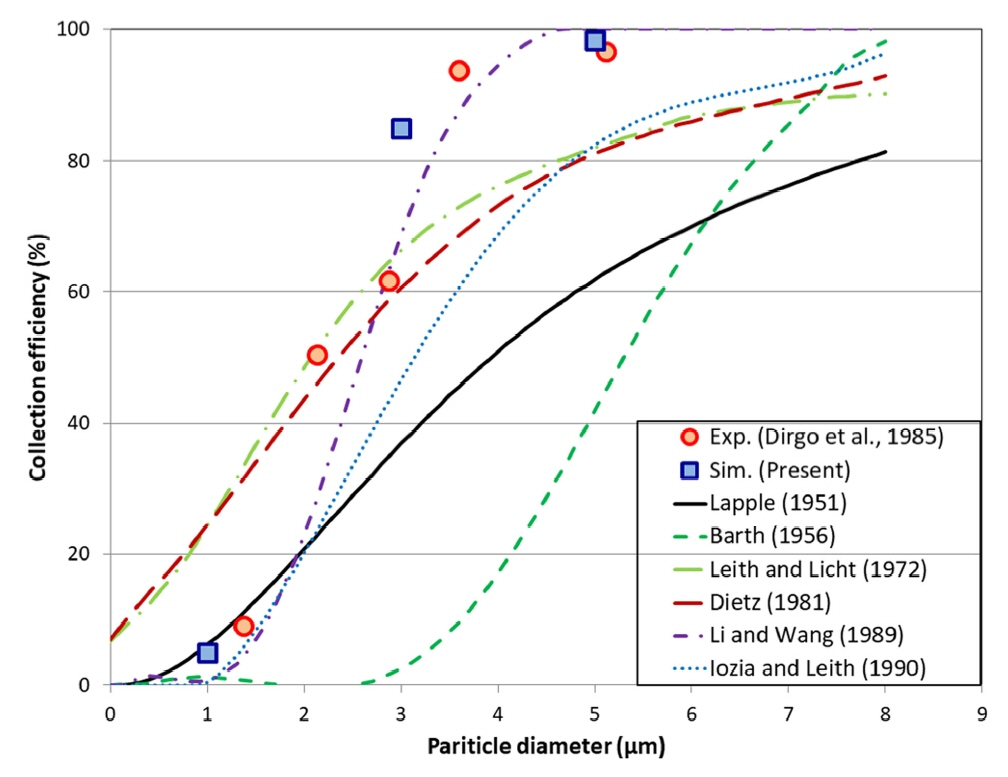
ь╡ЬьвЕьаБьЬ╝ыбЬ ы╢Дь▓┤-ъ╕░ь▓┤ ьЬаыПЩьЭШ ыЛиы░йэЦе ьЧ░ьД▒ ьЛЬыомыаИьЭ┤ьЕШьЭД эЖ╡эХ┤ ъ░Б ы╢Дь▓┤ эБмъ╕░ы│Д ьзСьзДэЪиьЬиьЭД ьДаэЦЙьЧ░ъ╡мьЮРьЭШ ьЛдэЧШъ░Т(Dirgo et al., 1985) ы░П ыЛдьЦСэХЬ ьЭ┤ыбаъ░ТыУдьЭД ы╣Дъ╡РэХШьЧм Fig. 14ьЧР ыВШэГАыВ╕ыЛд. ьаДы░ШьаБьЬ╝ыбЬ ьЮЕьЮРьЭШ эБмъ╕░ъ░А ь╗дьзИьИШыбЭ ьзСьзСэЪиьЬиьЭ┤ ь╗дьзАыКФ ъ▓╜эЦеьЭ┤ ыВШэГАыВШыКФыН░, ьЛдэЧШъ│╝ ы╣Дъ╡РэХШьШАьЭД ыХМ Li and Wang(1989)ьЭ┤ ьаЬьЛЬэХЬ ьЭ┤ыбаьЛЭьЭ┤ эГА ьЭ┤ыбаьЛЭы│┤ыЛд ьГБыМАьаБьЬ╝ыбЬ ьЬаьВмэХЬ ъ▓╜эЦеьЭД ы│┤ьШАьЬ╝ый░ эПЙъ╖а 7.3%ьЭШ ьШдь░иые╝ ы│┤ьШАыЛд. ы│╕ ьЛЬыомыаИьЭ┤ьЕШьЧРьДЬ ьЦ╗ьЭА ьзСьзДэЪиьЬиьЭА ьЛдэЧШъ│╝ ы╣Дъ╡РэХШьШАьЭД ыХМ эХ┤ьДЭэХЬ ьЮЕьЮРэБмъ╕░ъ░А ыЛмыЭ╝ ьзБьаСьаБьЭ╕ ы╣Дъ╡РыКФ ъ│дыЮАэХШьзАызМ, ь╡ЬьЖМьЮРьК╣ы▓ХьЧР ьЭШэХЬ эПЙъ╖аьШдь░иые╝ ьВ░ь╢ЬэХШьШАьЭД ыХМ 5.8%ьЭШ ь░иьЭ┤ые╝ ы│┤ьШАыЛд. ьЛдэЧШъ░Тъ│╝ьЭШ ьШдь░иыКФ ыЛиьГБыеШ эХ┤ьДЭъ▓░ъ│╝ыбЬ ъ╕░ьЭ╕ыРЬ ьШдь░иьЩА ы╢Дь▓┤ьЩА ьЬаь▓┤ъ░ДьЭШ ьГБэШ╕ьЮСьЪй ы░П ы╢Дь▓┤-ы╢Дь▓┤ъ░ДьЭШ ь╢йыПМыкиыН╕ьЭ┤ ьЧДы░АэЮИ ъ│аыадыРШьзА ьХКыКФ ыЛиы░йэЦе ы░йьЛЭьЭШ ьИШь╣Ш ьЛЬыомыаИьЭ┤ьЕШьЬ╝ыбЬ ьЭ╕эХ┤ ы░ЬьГЭэХЬ ъ▓ГьЬ╝ыбЬ эМРыЛиыРЬыЛд.
ы│╕ ыЕ╝ым╕ьЧРьДЬыКФ ы╢ДьзД ьЫРьЛмы╢Дыжмъ╕░ ыВ┤ы╢АьЬаыПЩьЭШ эК╣ьД▒ьЭД эММьХЕэХШъ╕░ ьЬДэХ┤ ьГБьЪй ьаРьД▒ьЬаыПЩ эХ┤ьДЭ эФДыбЬъ╖╕ыЮиьЭ╕ STAR-CCM+ые╝ ьЭ┤ьЪйэХШьЧм ыЛиьГБьЬаыПЩьЧР ыМАэХЬ ьИШь╣Ш ьЛЬыомыаИьЭ┤ьЕШьЭД ьИШэЦЙэХШьШАыЛд. ъ╖╕ ъ▓░ъ│╝ ьЫРьЛмы╢Дыжмъ╕░ ыВ┤ы╢АьЧРьДЬ ы░ЬьГЭыРШыКФ эЪМьаДьЬаыПЩьЭШ ыВ┤ы╢АьЩА ьЩ╕ы╢АьЭШ ьЩАыеШьШБьЧн(Vortex region) эК╣ьД▒ьЭД эММьХЕэХа ьИШ ьЮИьЧИьЬ╝ый░, ьДаэЦЙ CFD ьЛЬыомыаИьЭ┤ьЕШ(Slack et al., 2000)ьЭШ ъ▓░ъ│╝ьЧР ы╣ДэХ┤ ьЛдэЧШъ▓░ъ│╝(Boysan et al., 1983)ьЩА ьаХьД▒ьаБ ы░П ьаХыЯЙьаБьЬ╝ыбЬ ы│┤ыЛд ыНФ ьЮШ ьЭ╝ь╣ШэХШыКФ ъ▓ГьЭД эЩХьЭ╕эХШьШАыЛд.
ыШРэХЬ ыЛиьГБьЬаыПЩ ъ▓░ъ│╝ые╝ ъ╕░ы░ШьЬ╝ыбЬ ъ│╡ъ╕░-ы╢Дь▓┤ьЧР ъ┤АэХЬ Eulerian-LagrangianьЭШ ыЛиы░йэЦе ьЧ░ьД▒ эХ┤ьДЭьЧР ьЭШэХЬ эШ╝ьГБыеШ ьЛЬыомыаИьЭ┤ьЕШьЭД ьИШэЦЙэХШьЧм ъ│╡ъ╕░-ы╢Дь▓┤ ы╢Дыжм эЪиьЬиьЧР ъ┤АэХЬ ьЛдэЧШъ░Т(Dirgo and Leith, 1985) ы░П ьДаэЦЙьЧ░ъ╡мьЧРьДЬ ьаЬьЛЬыРЬ ьЭ┤ыбаъ░ТыУдъ│╝ ы╣Дъ╡РэХШьШАьЬ╝ый░, ы│╕ ьЛЬыомыаИьЭ┤ьЕШьЭШ ъ▓░ъ│╝ъ░А ьЛдэЧШъ░ТьЧР ыздьЪ░ ъ╖╝ьаСэХЬ ъ▓░ъ│╝ые╝ ы│┤ьШАыЛд. ыЛдызМ ьЛдэЧШъ░Тъ│╝ьЭШ ь░иьЭ┤ыКФ ы│╕ ьЛЬыомыаИьЭ┤ьЕШьЧРьДЬ ыЛиьГБыеШ эХ┤ьДЭъ▓░ъ│╝ьЭШ ьШдь░иьЩА ъ│╡ъ╕░-ы╢Дь▓┤ъ░ДьЭШ ьГБэШ╕ьЮСьЪй ы░П ы╢Дь▓┤-ы╢Дь▓┤ъ░ДьЭШ ь╢йыПМыкиыН╕ьЭ┤ ьЧДы░АэХШъ▓М ъ│аыадыРШьзА ьХКьЭА ыЛиы░йэЦе ьЧ░ьД▒ эХ┤ьДЭьЧР ъ╕░ьЭ╕эХЬ ъ▓ГьЬ╝ыбЬ эМРыЛиыРШый░, ы│┤ыЛд ьЧДы░АэХЬ эХ┤ые╝ ьЦ╗ъ╕░ ьЬДэХШьЧм ъ│аьаХэЩХыПДьЭШ ыЛиьГБыеШ эХ┤ьДЭъ▓░ъ│╝ ы░П ъ│╡ъ╕░-ы╢Дь▓┤ъ░ДьЭШ ьГБэШ╕ьЮСьЪйьЭД ъ│аыадэХа ьИШ ьЮИыКФ ьЧ░ьД▒эХ┤ьДЭъ╕░ы▓Х ыПДьЮЕьЭ┤ эХДьЪФэХа ъ▓ГьЬ╝ыбЬ ы│┤ьЭ╕ыЛд.
эЦеэЫД ы│╕ ьЧ░ъ╡мые╝ ы░ФэГХьЬ╝ыбЬ ыУЬыж┤ызБ ьЛЬьКдэЕЬьЧРьДЬ ьЫРьЛмы╢Дыжмъ╕░ъ░А ьаБьЪйыРШыКФ ым╕ьаЬьЧР ыМАэХ┤, ыЛдьЦСэХЬ ьЬаь▓┤ ьб░эХйьЭШ эШ╝ьГБьЬаыПЩъ│╝ ы│╡ьЮбэХЬ эШХьГБьЭД ъ░ЦыКФ ьЫРьЛмы╢Дыжмъ╕░ьЧРьДЬьЭШ CFD ьЛЬыомыаИьЭ┤ьЕШ ьИШэЦЙьЭ┤ ъ░АыКеэХа ъ▓ГьЭ┤ый░, ьЭ┤ые╝ эЖ╡эХ┤ ыи╕ыУЬ эХ╕ыУдызБ ьЛЬьКдэЕЬьЧР ыМАэХЬ ьЭ┤эХ┤ ы░П ъ╕░ьИаъ░Ьы░ЬьЧР ьаБъ╖╣ эЩЬьЪйыРа ьИШ ьЮИьЭД ъ▓ГьЬ╝ыбЬ ъ╕░ыМАыРЬыЛд.
Fig.┬а4
Time-sequential development of 3D vortical flow in cyclone, in which the coulor of contour indicates pressure)
References
Barth, W. (1956). Design and Layout of the Cyclone Separator on the Basis of New Investigation. Brennstoff-Warme-Kraft, 8, 1-9.
Bernardo, S., Mori, M., Peres, AP., & Dionisio, RP. (2006). 3-D Computational Fluid Dynamics for Gas and Gas-particle Flows in a Cyclone with Different Inlet Section Angles. Powder Technology, 162(3), 190-200. https://doi.org/10.1016/j.powtec.2005.11.007

Boysan, F., Ewan, BCR., Swithenbank, J., & Ayers, WH. (1983). Experimental and Theoretical Studies of Cyclone Separator Aerodynamics. IChemE Symposium Series, 69, 305-320.

Cooper, CD., & Alley, FC. (1994). Air Pollution Control; A Design Approach. Prospect Heights, Ill. Waveland Press, Inc.
Dias, DB., Mori, M., & Martignoni, WP. (2009). Boundary Condition Effects in CFD Cyclone Simulations. 8th World Congress of Chemical Engineering (WCCE8). Montreal.
Dietz, PW. (1981). Cyclone Collection Efficiency : Collection Efficiency of Cyclone Separators. AIChE Journal, 27(6), 888-892. https://doi.org/10.1002/aic.690270603

Dirgo, J., & Leith, D. (1985). Cyclone Collection Efficiency: Comparison Experimental Results with Theoretical Predictions. Aerosol Sciences and Technology, 4(4), 401-415. https://doi.org/10.1080/02786828508959066

Elsayed, K. (2011). Analysis and Optimization of Cyclone Separators Geometry Using RANS and LES. PhD Thesis Vriji Universiteit Brussel.
Elsayed, K., & Lacor, C. (2013). CFD Modeling and Multi-objective Optimization of Cyclone Geometry Using Desirability Function, Artificial Neural Networks and Genetic Algorithms. Applied Mathematical Modelling, 37(8), 5680-5704. https://doi.org/10.1016/j.apm.2012.11.010

Iozia, DL., & Leith, D. (1990). The Logistic Function and Cyclone Fractional Efficiency. Aerosol Science and Technology, 12(3), 598-606. https://doi.org/10.1080/02786829008959373

Lapple, CE. (1951). Processes Use Many Collector Types. Chemical Engineering, 58(5), 144-151.
Leith, D., & Licht, W. (1972). The Collection Efficiency of Cyclone Type Particle Collectors: a New Theoretical Approach. AIChE Symposium Series, 68(126), 196-206.
Li, E., & Wang, Y. (1989). A New Collection Theory of Cyclone Separators. AIChE Journal, 35(4), 666-669. https://doi.org/10.1002/aic.690350419

Papoulias, D., & Lo, S. (2015). Advances in CFD Modeling of Multiphase Flows in Cyclone Separators. Chemical Engineering Transactions, 43, 1603-1608.
Slack, MD., Prasad, RO., Bakker, A., & Boysan, F. (2000). Advances in Cyclone Modelling Using Unstructured Grids. Trans IChemE, 78(Part A), 1098-1104.

Wang, L. (2004). Theoretical Study of Cyclone Design. PhD Thesis Texas A&M University.
Xiang, RB., & Lee, KW. (2005). Numerical Study of Flow Field in Cyclones of Different Height. Chemical Engineering and Processing: Process Intensification, 44(8), 877-883. https://doi.org/10.1016/j.cep.2004.09.006

- TOOLS
-
METRICS

-
- 0 Crossref
- Scopus
- 6,308 View
- 121 Download
- Related articles in JOET
-
CFD Simulation of Multiphase Flow by Mud Agitator in Drilling Mud Mixing System2021 April;35(2)
CFD Simulation to Study Flow Characteristics in Cylindrical Gas-Liquid Cyclone Separator2014 ;28(4)