고립파(지진해일)의 파형분포가 불투과 경사면의 처오름에 미치는 영향
Effects of Waveform Distribution of Tsunami-Like Solitary Wave on Run-up on Impermeable Slope
Article information
Trans Abstract
For decades, solitary waves have commonly been used to simulate tsunami conditions in numerical studies. However, the main component of a tsunami waveform acts at completely different spatial and temporal distributions than a solitary waveform. Thus, this study applied a 2-D numerical wave tank that included a non-reflected tsunami generation system based on Navier-Stokes equations (LES-WASS-2D) to directly simulate the run-up of a tsunami-like solitary wave on a slope. First, the waveform and velocity due to the virtual depth factor were applied to the numerical wave tank to generate a tsunami, which made it possible to generate the wide waveform of a tsunami, which was not reproduced with the existing solitary wave approximation theory. Then, to validate the applied numerical model, the validity and effectiveness of the numerical wave tank were verified by comparing the results with the results of a laboratory experiment on a tsunami run-up on a smooth impermeable 1:19.85 slope. Using the numerical results, the run-up characteristics due to a tsunami-like solitary wave on an impermeable slope were also discussed in relation to the volume ratio. The maximum run-up heights increased with the ratio of the tsunami waveform. Therefore, the tsunami run-up is highly likely to be underestimated compared to a real tsunami if the solitary wave of the approximation theory is applied in a tsunami simulation in a coastal region.
1. 서 론
2004년 12월 26일에 인도네시아 수마트라 서부 해안의 40km지점에서 발생한 해저지진에 의해 지진해일은 약 30만 명의 사망/실종자, 약 120억 달러의 재산피해를 발생시켰다. 2011년 3월 11일에 일본 미야기현 센다이에서 동쪽으로 70km 떨어진 지점의 해저지진에 의한 지진해일은 약 3만 명의 사망/실종자, 약 2,350억 달러의 재산피해를 발생시켰다. 이 같은 지진해일은 막대한 인⋅물적 피해를 야기 시킨다.
Fig. 1은 한반도 주변에서 발생한 해저지진의 분포도이고, Fig. 2는 매년 발생한 해저지진해일 횟수를 나타낸 것이다. Fig. 1과 Fig. 2의 기상청에서 보고한 자료를 살펴보면, ‘우리나라는 지진해일에 안전한가?’라는 의문이 생기기 마련이다. 여기에 우리나라의 동해안에서는 약 50년 사이에 지진해일에 의한 피해가 1964년 M7.5의 니가타 지진해일, 1983년 M7.5의 동해중부 지진해일, 1993년 M7.8의 북해도 남서외해 지진해일이 보고되었다. 특히 1983년에 발생한 지진해일은 임원항에 내습하여 최대 3~5m의 처오름 흔적을 남겼고, 3명의 사망/실종자, 약 4억원의 재산피해를 입혔다. 우리나라도 더 이상 지진해일에 안전지대가 아니며, 잠재적 위험지역으로 볼 수 있다.
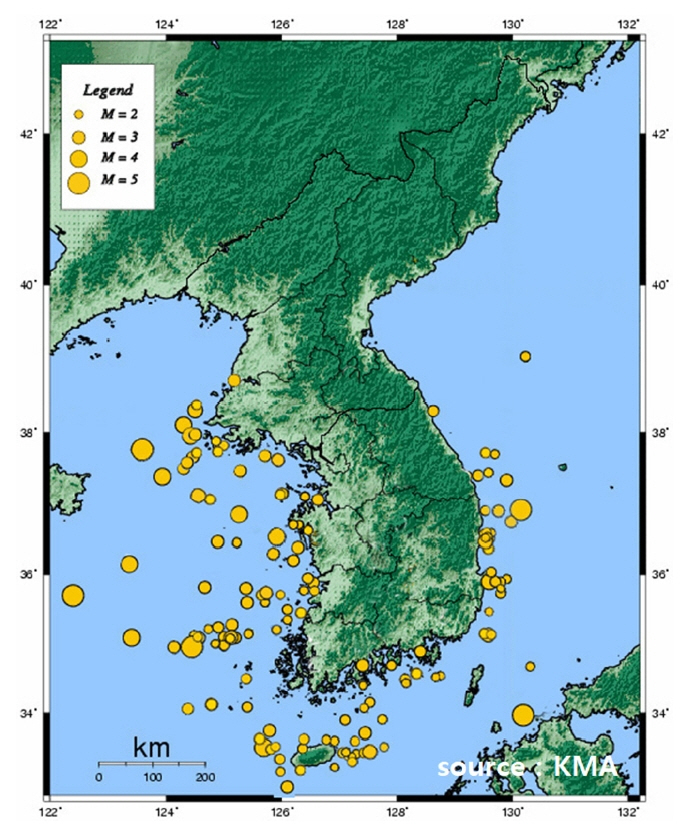
Distribution of submarine earthquake around the Korean Peninsula (Source: Korea Meteorological Administration)
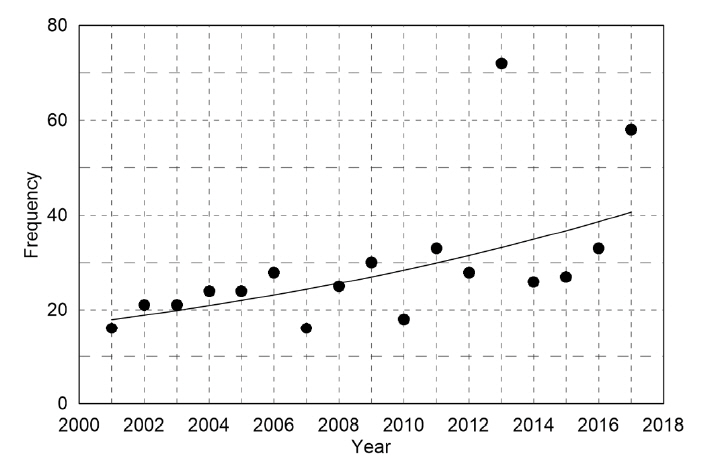
Occurrences frequency of submarine earthquake around Korea Peninsula (Source: Korea Meteorological Administration)
이에 국내⋅외적으로 지진해일 피해에 대한 경각심을 가지고 다양한 분야에서 많은 연구자들이 지진해일의 발생, 전파 그리고 수리현상을 파악하는 것에 노력을 기울이고 있다. 그 중에서 지진해일에 의한 직접적인 피해원인이 되는 충격파, 처오름, 월파, 침수 등에 관한 연구에서는 수십 년간 지진해일과 파형이 유사한 고립파 근사값을 입사조건으로 이용해 왔다(Synolakis, 1986; Synolakis, 1987; Zelt, 1991a; Zelt, 1991b; Li, 2000; Tonkin et al., 2003). 그러나 Qu et al.(2017a)과 Qu et al.(2017b)에 따르면, Fig. 3처럼 2011년 동일본에 관측된 지진해일은 고립파에 비해 매우 넓게 분포하는 것을 확인할 수 있다. 이것은 수리실험 및 수치모의에서 고립파 근사이론에 의한 입사조건을 적용할 경우, 실제 발생하는 지진해일보다 충격파, 처오름, 월파, 침수같은 재해규모가 과소평가될 수 있다. 이것을 보완하기 위해 수조실험에서는 조파기의 스트로크 및 이동속도를 조절(Park et al, 2013), 붕괴파(Nouri et al, 2010; (Liu et al., 2014), 공기압축식(Rossetto et al, 2011), 대용량 펌프(Goseberg, 2012) 등을 통해 넓은 파형의 지진해일 생성한다. 수치파동수조에서는 고립파 근사이론에 근거하여 분포를 조절(Lee et al., 2016), Fig. 3처럼 파형을 중첩(Qu et al., 2017a; Qu et al., 2017b)하여 넓은 고립파형의 지진해일을 발생시킨다.
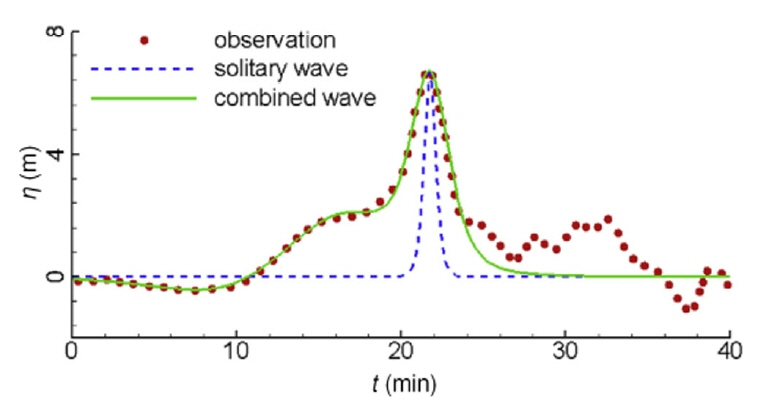
Comparisons between the observed tsunami waveform and the solitary waveform based on approximation theory (Source: Qu et al., 2017a)
국내에서는 해저 지각활동에 따른 지진해일의 발생과 전파특성을 분석하기 위한 연구들이 활발하게 수행되고 있다(Cho and Lee, 2002; Kim et al., 2007a; Kim et al., 2007b; Kim et al., 2008). 그리고 직접적인 인명피해의 원인이 되는 처오름, 월파, 침수에도 실험수조 또는 수치수조에서 고립파형의 지진해일을 직접 발생시켜 그 현상을 조사하였다(Ha et al., 2010; Ha et al., 2012; Lee and Kim, 2014; Hur et al., 2015; Lee et al., 2018). 국외에서는 (Liu et al.(2006)과 Chang et al.(2009)은 1:20 경사면 상을 전파하는 고립파의 파형, 파고, 처오름 등을 측정하여 보고하였으며, 수치모델 검증에 많이 이용되고 있다. Hunt-Raby et al.(2011)은 고립파 및 파군형성에 따른 월파현상을 수리수조에서 측정하였다. Baldock et al.(2012)는 일정한 경사를 전파하는 고립파의 처오름과 월파량을 측정한 수리실험에서 파고와 수심과의 비, 파고와 월파수조 높이와의 비와 월파량과의 관계를 분석하였다. Bozorgnia et al.(2014)은 2차원 CFD(Computational fluid dynamic)에서 고립파를 생성하여 방파제에서 월파모의를 수행하였으며, 기존실험에서 측정한 수면변위와 유속을 고정도로 재현하였다.
이상의 활발한 국내⋅외 연구들도 모두 고립파를 대상으로 하고 있기 때문에 지진해일에 의한 수리특성이 과소평가 될 우려가 크다. 따라서 본 연구에서는 고립파형 지진해일의 파형분포에 따른 경사면 상의 처오름 특성을 논의하기 위하여 Lee et al.(2016)이 제안한 조파방법과 2차원 수치파동수조(Hur et al., 2011)를 결합하여 지진해일 처오름 모의를 수행한다. 먼저 이용하는 수치파동수조의 타당성 및 유효성을 입증하기 위하여 1:19.85 경사면 주변에서 Synolakis(1987)가 측정한 수면형과 모의한 시⋅공간파형을 비교⋅검토한다. 그리고 지진해일 처오름 모의를 통해 파형분포가 처오름 현상이 미치는 영향을 정성/정량적으로 분석한다.
2. 수치파동수조
본 연구에서는 고립파형 지진해일의 파형분포가 경사면 처오름에 미치는 영향을 분석하기 위한 수치모의를 수행한다. 수치모의에 이용하는 수치모델은 Hur et al.(2011)를 토대로 개량한 Lee et al.(2018)의 Numerical wave tank(NWT)이다. 이 수치모델은 강비선형 2-D Navier-Stokes(N-S) solver로서 지진해일의 수리현상을 직접 해석할 수 있다. 그리고 이 수치모델에서는 Lee et al.(2016)이 제안한 고립파형 지진해일 조파방법을 적용한다.
2.1 지배방정식
지배방정식은 비압축성⋅점성유체 조건에서 지진해일을 생성할 수 있게 무반사 조파시스템이 도입된 연속방정식 (1)과 Porous body model(PBM)에 기초한 N-S 운동량 방정식 (2)로 구성된다.
여기서 vi는 x, z방향의 유속, q*는 소스의 유량밀도, γυ는 체적 공극률, γi는 x, z방향의 면적 공극률, t는 시간, ρ는 유체 밀도, p는 압력, νT는 유체의 동점성계수(ν)와 와동점성계수(νt)의 합, Dij는 변형률속도텐서, Si는 Continuum surface force(CSF)(Brackbill et al., 1992)모델에 기초한 표면장력항, Qi 파랑 또는 흐름의 소스항, Ri는 식생에 의한 유체저항항, gi는 중력가속도항, Ei는 부가감쇠영역의 에너지 감쇠항이다.
F는 각 격자에서 유체가 차지하고 있는 체적비이며, 연속방정식 (1)에 비압축성 유체에 대한 가정과 PBM을 토대로 VOF(Volume of fluid)함수를 적용하면, 식 (3)과 같이 유체 보존형식으로 나타낼 수 있다.
2.2 지진해일 조파방법
수치파동수조에서 조파원천의 양쪽방향(x의 ±방향)으로 파랑이 생성되기 때문에 상수 2를 고려한 생성강도(q)는 Brorsen and Larsen(1987)의 식 (4)를 이용한다. 그리고 수치파동수조 내의 장애물 또는 경계로부터 발생하는 반사파의 영향을 최소화하기 위하여 Ohyama and Nadaoka(1991)가 제안한 강도조절계수(ζ)을 적용하여 안정적으로 지진해일을 조파한다.
여기서 V0는 근사이론에 의한 파랑의 수평유속성분, ζ는 강도조절계수(
이 수치파동수조는 엇갈림 격자체계임으로 식 (5)과 같이 지진해일 생성지점의 격자크기(∆xs)에 따른 생성강도(q)의 영향을 배제하기 위해 유량밀도(q*)를 도입한다.
Lee et al.(2016)는 Dean and Dalrymple(1984)의 고립파 근사이론에 기초하여 다양한 고립파형의 지진해일을 생성할 수 있는 분포계수(α)와 가상수심계수(β)를 제안하였다. Lee et al.(2018)에서 2차원 수치파동수조에 지진해일 조파방법을 도입하였다. Lee et al.(2016)이 제안한 고립파형 지진해일의 시간파형과 각 수심별 수평유속은 다음의 식 (6)-(7)과 같다.
여기서 Hi는 지진해일고, h는 수심, C는 식 (8)과 같은 파속, λ는 근사수면변위와 해일고와의 비(=η/Hi), ∊는 해일고와 수심과의 비(=Hi/h), zh는 바닥과 수립자의 연직거리와 수심과의 비이다.
2.3 수치파동수조의 검증
고립파형 지진해일의 파형분포에 따른 처오름 특성을 분석하기에 앞서 이용하는 2차원 수치파동수조의 타당성 및 유효성을 검증한다. 먼저 지진해일 조파방법을 검증하기 위하여 가상수심계수(β)에 따른 파형과 유속을 비교한다. 그리고 지진해일 처오름 시, 불투과 경사면 상의 시⋅공간 파형을 검증한다.
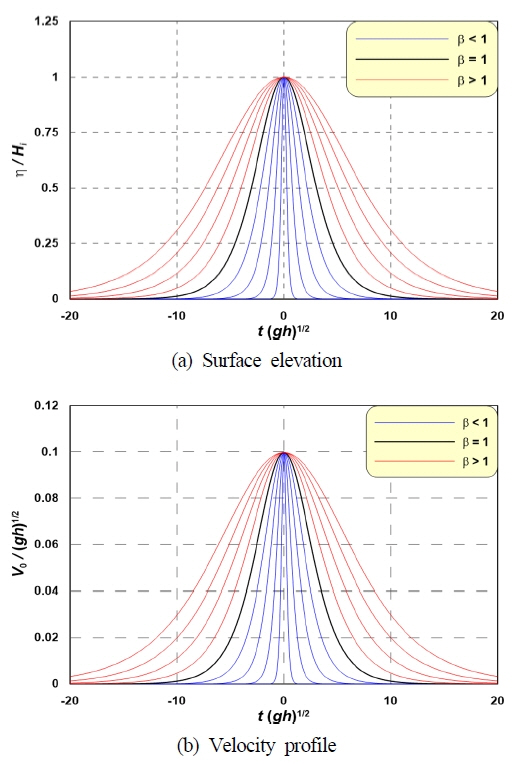
Fig. 4는 수심 100cm, 지진해일고 10cm일 때, Dean and Dalrymple(1984)의 고립파 근사식에 β를 적용하여 구한 지진해일의 수리특성이다. Fig. 4에서 (a)는 시간파형, (b)는 정수면에서의 유속분포를 나타낸다. (a)와 (b)의 그래프에서 파란색 실선은 β < 1, 검정색 실선은 β = 1, 빨간색 실선은 β > 1의 경우를 각각 의미한다.
Fig. 4에서 β에 따른 다양한 파형 및 유속분포가 형성되고, 선형적인 증감하는 것을 확인할 수 있다. Fig. 4(a)에서는 β > 1이며 Dean and Dalrymple(1984)의 고립파 근사파형보다 넓은 파형분포, β < 1이면 좁은 파형분포를 나타낸다. Fig. 4(b)에서는 전술한 파형분포에 상응하는 유속값을 가지는 것을 알 수 있다.
이상에 근거하여 미루어 볼 때, Dean and Dalrymple(1984) 근사식에 β를 대입하여 다양한 파형 그리고 이것에 상응하는 유속분포를 수치파동수조에 적용하여 실제에 가까운 지진해일을 얻을 수 있을 것이다.
본 연구에서 적용하는 2차원 수치파동수조의 타당성 및 유효성을 검증하기 위하여 Fig. 5와 같은 Synolakis(1987)의 경사면 처오름에 관한 수리모형실험에 근거한 수치파동수조를 이용한다. 수심 20cm의 해석영역에 1:19.85의 불투과성 경사면을 설치하고, 안정적 지진해일 조파를 위해 외해에는 조파소스, 감쇠영역, 개경계 조건을 고려한다. 수치수조의 수평격자는 2cm, 수직격자는 0.2cm로 구성하고, 1/1000초 간격으로 계산을 수행한다.
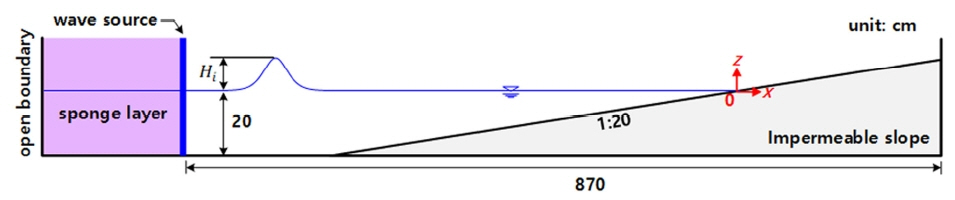
Schematic diagram of a numerical wave tank based on Synolakis (1987)’s experimental one
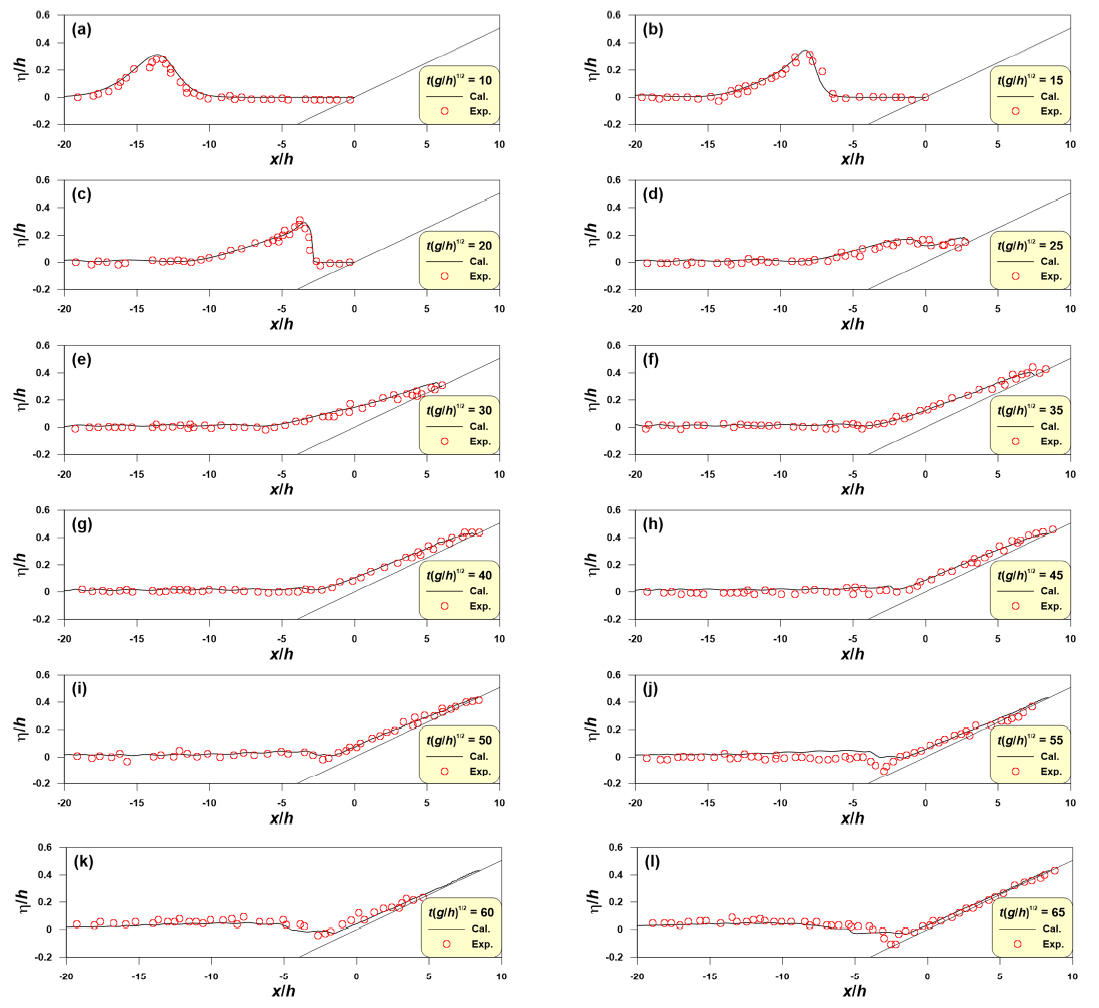
Fig. 6은 높이 6cm의 고립파가 불투과 경사면으로 내습할 때의 시⋅공간 파형분포를  )은 Synolakis(1987)의 수리실험에서 측정된 수면형, 검정색 실선(−)은 수치파동수조에서 얻은 수면형이다.
)은 Synolakis(1987)의 수리실험에서 측정된 수면형, 검정색 실선(−)은 수치파동수조에서 얻은 수면형이다.
Fig. 6(a)-(c)에서는 외해에서 유입되는 고립파의 비선형성이 증가하여 경사면 상에서 발생한다. Fig. 6(d)-(g)에서는 고립파쇄파 이후에 경사면 상으로 전파되고, Fig. 6(g)에서 최대 처오름 높이를 나타낸다. Fig. 6(h)-6(l)에서는 경사면을 따라 처내림이 발생함을 확인할 수 있다. 이와 같은 불투과 경사면 상의 고립파 전파과정을 수치모의결과가 Synolakis(1987)의 실험결과를 매우 잘 재현하고 있다.
이상의 검증결과에 근거하여 수치파동수조에 도입한 지진해일 조파방법, 지진해일 처오름 모의를 위한 수치파동수조의 유효성 및 타당성이 입증되었다고 판단된다.
3. 수치모의결과
3.1 시⋅공간파형분포
Fig. 7은 5cm의 고립파형 지진해일이 경사면으로 내습하여 최대 처오름이 발생하는 시점에서 입사파형에 따른 수면형의 공간분포를 나타낸다. Fig. 7에서 검은색 실선(─)은 Dean and Dalrymple(1984)의 고립파 근사이론에 의한 고립파가 유입되는 경우(V/V0= 1), 파란색 실선( )은 근사파형보다 좁은 경우(V/V0 < 1) 그리고 빨간색 실선(
)은 근사파형보다 좁은 경우(V/V0 < 1) 그리고 빨간색 실선( )은 근사파형보다 넓은 경우(V/V0 > 1)를 각각 의미한다. 그래프의 종축은 수평거리(x)를 유효파장(Leff), 횡축은 수면변위(η)를 입사 해일고(Hi)로 각각 무차원화 한다. 여기서, Leff는 Dean and Dalrymple(1984)의 고립파형의 약 95% 체적에 해당하는 파장이고, 식 (9)로부터 구할 수 있다.
)은 근사파형보다 넓은 경우(V/V0 > 1)를 각각 의미한다. 그래프의 종축은 수평거리(x)를 유효파장(Leff), 횡축은 수면변위(η)를 입사 해일고(Hi)로 각각 무차원화 한다. 여기서, Leff는 Dean and Dalrymple(1984)의 고립파형의 약 95% 체적에 해당하는 파장이고, 식 (9)로부터 구할 수 있다.
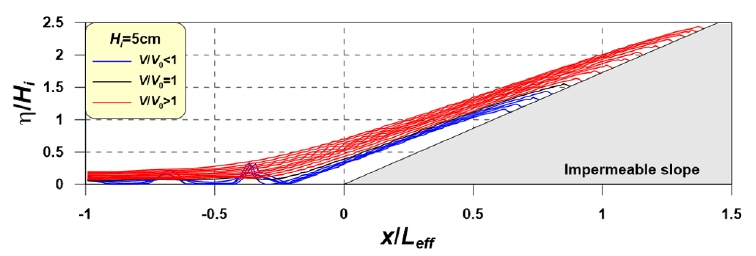
Spatial-domain waveform of tsunami-like solitary wave due to the volume ratios in case of the maximum run-up height
Fig. 7로부터 고립파형 지진해일의 입사파형이 넓을수록(V/V0가 클수록) 경사면 상의 수면형이 넓게 분포하고, 처오름이 뚜렷하게 증가하는 경향을 보인다. 이러한 경향은 V/V0가 클수록 지진해일의 공간파형이 넓게 분포함으로써 처오름 시에 지속적으로 밀어주는 유속과 해안으로 유입되는 유체량이 증가한다. 그리고 V/V0가 클수록 파장이 길기 때문에 먼저 도달한 지진해일이 중첩의 영향에 의한 수위 상승이 처오름을 더욱 가중시키는 것으로 이해된다.
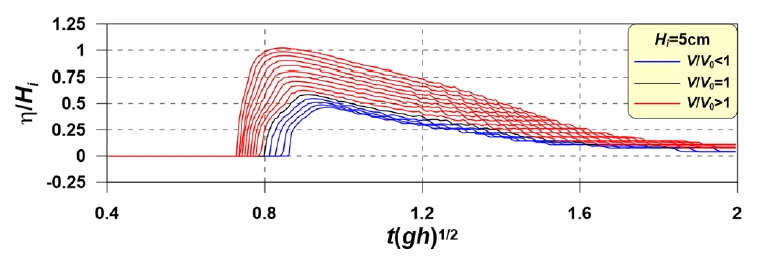
Fig. 8는 고립파형 지진해일이 내습하는 동안 정선(x/Leff = 0)에서의 수면형의 시간분포를 나타내며, 검은색 실선(─)은 근사 고립파의 경우(V/V0 = 1), 파란색 실선( )은 근사파형보다 좁은 경우(V/V0 < 1) 그리고 빨간색 실선(
)은 근사파형보다 좁은 경우(V/V0 < 1) 그리고 빨간색 실선( )은 근사파형보다 넓은 경우(V/V0 > 1)이다. Fig. 8의 그래프에서 종축은 고립파형 지진해일의 특성을 파악하기 위해 시간에 파속을 곱해 이동거리(t(gh)1/2)로 나타내고, 횡축은 η를 Hi로 무차원한다.
)은 근사파형보다 넓은 경우(V/V0 > 1)이다. Fig. 8의 그래프에서 종축은 고립파형 지진해일의 특성을 파악하기 위해 시간에 파속을 곱해 이동거리(t(gh)1/2)로 나타내고, 횡축은 η를 Hi로 무차원한다.
Fig. 8에서 V/V0가 클수록 정선(x/Leff = 0)에서의 최대지진해일고가 증가하고, 경사면과의 상호간섭 시점이 빨리질 뿐만 아니라, 시간파형도 넓게 분포한다. 따라서 지진해일의 공간분포에서 논의한 바와 같이 V/V0가 클수록 지진해일 처오름 시 밀어주는 유체량이 많으며, 더 긴 시간동안 처오름이 발생함으로 정선에서의 수위상승이 커진다.
3.2 파동장과 유동장
Fig. 9에는 x/Leff = 0에서의 내습하는 고립파형 지진해일이 최대 수위를 발생하는 시점에 불투과성 경사면 주변의 파동장과 유동장을 도시하며, 대표적으로 근사 고립파형보다 좁은 경우, 넓은 경우 그리고 근사 고립파형인 경우에 대해 각각 나타낸다. Fig. 9에서 (a)는 좁은 파형(V/V0 = 0.6), (b)는 고립파형(V/V0 = 1), (c)는 넓은 파형(V/V0 = 2)이다.
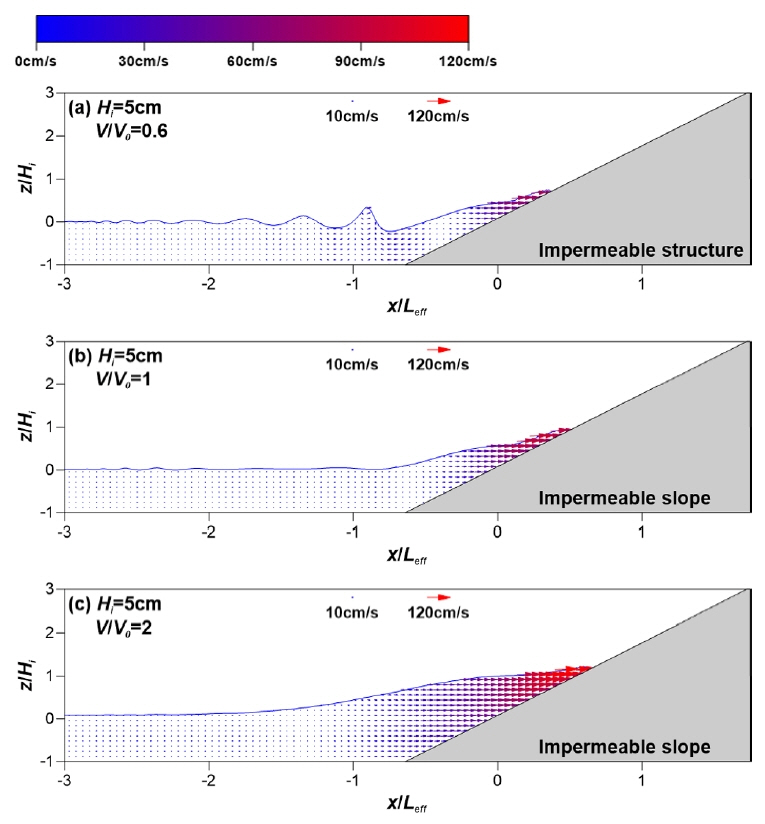
Spatial distributions of free surface elevations and velocities by a tsunami-like solitary wave in the vicinity of an impermeable slope
Fig. 9으로부터 V/V0가 클수록 경사면 상의 유체범위가 넓게 분포하고, 처오름 수괴의 선단 유속이 큰 것을 알 수 있다. 그리고 경사면 상에서 처오름을 지속적으로 발생시킬 수 있는 수평 방향의 후속유속이 넓게 분포한다. 이와 같은 유속분포는 V/V0가 클수록 뚜렷하며, 지진해일의 처오름에 있어서 유체를 지속적으로 경사면 상으로 밀어주어 처오름 높이를 증가시킬 것이다. 이처럼 예상되는 최대 처오름 높이 결과는 Fig. 7에서 확인할 수 있다.
3.3 정선에서의 연직유속분포
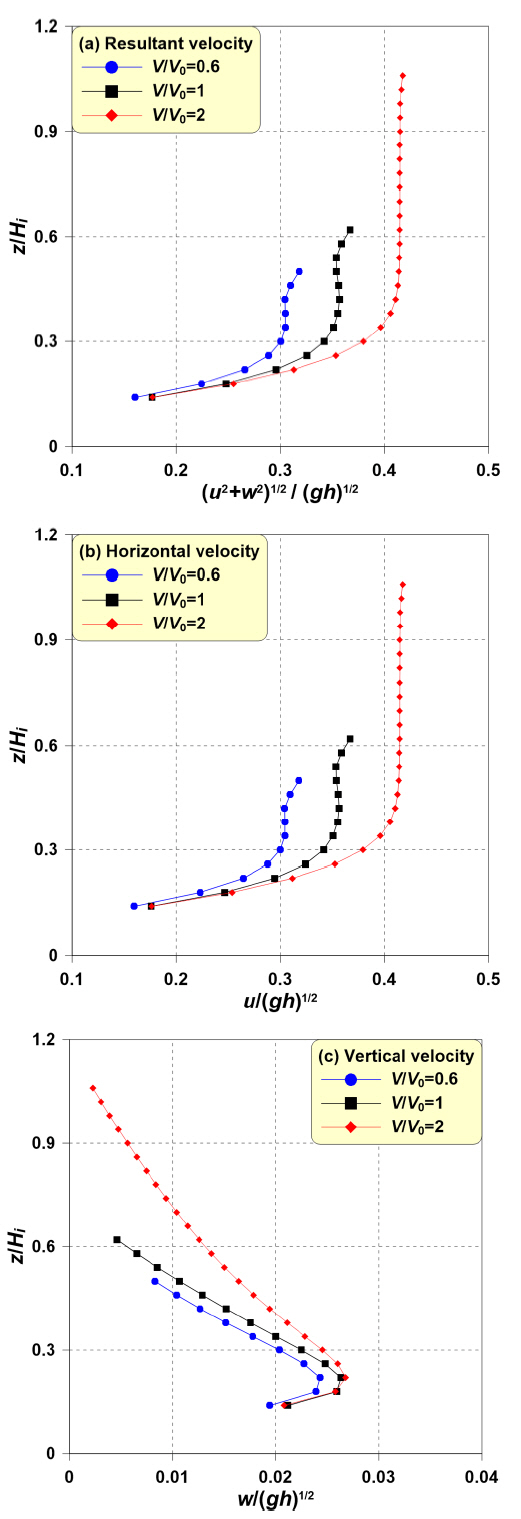
Fig. 10에서는 Fig. 9에서 x/Leff = 0 지점의 유속 및 x, z 방향의 유속성분의 연직분포를 나타낸다. Fig. 10에서 (a)는 유속, (b)는 수평유속성분, (c)는 수직유속성분의 연직분포이다. 그리고 파란색 원( )는 근사 고립파형보다 좁은 V/V0 = 0.6, 검정색 사각형(■)은 근사 고립파형인 V/V0 = 1, 빨간색 마름모(
)는 근사 고립파형보다 좁은 V/V0 = 0.6, 검정색 사각형(■)은 근사 고립파형인 V/V0 = 1, 빨간색 마름모( )는 근사 고립파형보다 넓은 V/V0 = 2를 각각 의미한다. 여기서 횡축은 유속을 파속(
)는 근사 고립파형보다 넓은 V/V0 = 2를 각각 의미한다. 여기서 횡축은 유속을 파속(
Fig. 10(a)에서는 전술한 Fig. 8에서 논의한 바와 같이 V/V0가 클수록 정선에서의 수위상승이 증가하기 때문에 V/V0 가 큰 경우에 유속의 연직분포도 넓다. 특히 쇄파가 발생하지 않는 V/V0 = 2가 유속의 연직분포가 높게 형성됨을 알 수 있다. Fig. 10의 (b)와 (c)에서는 점진적으로 단면이 축소되는 불투과 경사면 상으로 전파하는 지진해일의 수평유속이 지배적이고, V/V0가 클수록(지진해일의 파장이 길수록) 수직유속 성분보다 수평유속 성분이 발달함을 알 수 있다.
이상의 고립파형 지진해일 처오름 모의로부터 확인한 수리특성은 처오름 높이와 직결될 것으로 판단된다. 이에 다음 단락에서 근사 고립파 대비 지진해일의 체적비가 처오름 높이에 미치는 영향을 정량적 비교하여 실제 지진해일에 의한 처오름 높이를 가늠할 수 있는 논의를 진행하기로 한다.
3.4 처오름 높이
Fig. 12는 V/V0에 따른 고립파형 지진해일의 최대 처오름 높이를 비교한 것이다. Fig. 12에서 빨간색 마름모( )는 Hi = 3cm, 검정색 원(○)은 Hi = 5cm, 파란색 사각형(
)는 Hi = 3cm, 검정색 원(○)은 Hi = 5cm, 파란색 사각형( )은 Hi = 7cm의 경우이다. 그리고 빨간색 실선(
)은 Hi = 7cm의 경우이다. 그리고 빨간색 실선( )은 Hi = 3cm, 검정색 실선(―)은 Hi= 5cm, 파란색 실선(
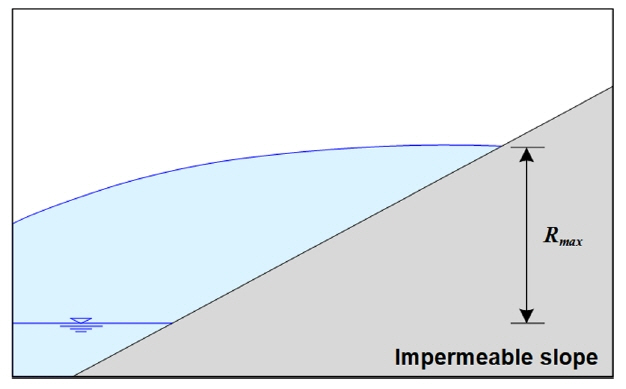
)은 Hi = 3cm, 검정색 실선(―)은 Hi= 5cm, 파란색 실선( )은 Hi = 7cm의 경우 경향선을 각각 나타낸다. 그래프에서 종축은 근사 고립파 대비 지진해일의 체적비(V/V0), 횡축은 지진해일의 최대 처오름 높이(Rmax)를 근사 고립파 내습 시의 최대 처오름 높이(R0)로 무차원한 것이다. 여기서 Rmax는 Fig. 11에 나타낸 것처럼 최대 처오름이 발생하는 시점에 정선과의 최단거리로 정의한다.
)은 Hi = 7cm의 경우 경향선을 각각 나타낸다. 그래프에서 종축은 근사 고립파 대비 지진해일의 체적비(V/V0), 횡축은 지진해일의 최대 처오름 높이(Rmax)를 근사 고립파 내습 시의 최대 처오름 높이(R0)로 무차원한 것이다. 여기서 Rmax는 Fig. 11에 나타낸 것처럼 최대 처오름이 발생하는 시점에 정선과의 최단거리로 정의한다.
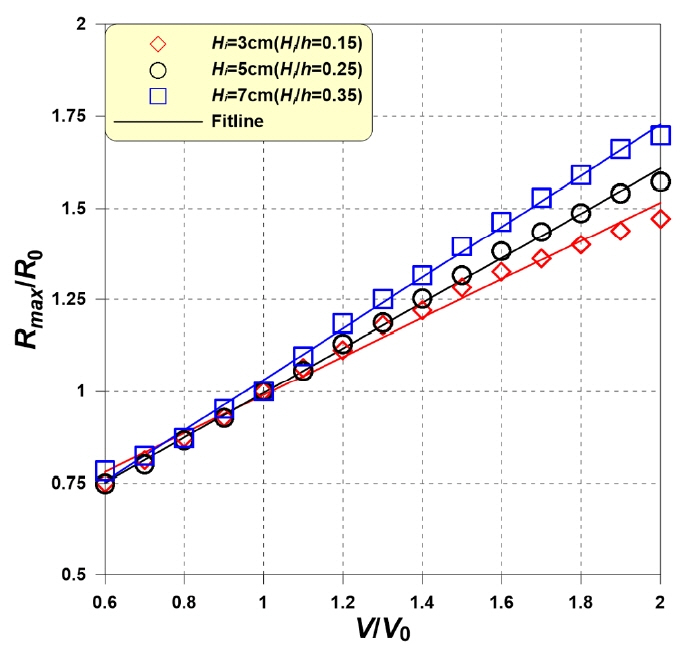
Run-up characteristics of tsunami-like solitary wave due to volumetric rates with tsunami wave height
Fig. 12에서 V/V0와 Rmax/R0는 비례관계이며, V/V0가 클수록 Rmax/R0가 급하게 증가한다. 그리고 V/V0 < 1인 경우에는 Hi에 따른 Rmax/R0의 차이가 작지만, V/V0 > 1인 경우에서는 Hi에 따른 Rmax/R0의 차이가 커진다. 동일한 V/V0에서 Hi가 클수록 Rmax/R0가 크다는 것은 높은 지진해일이 유입될 때 경사면 상의 처오름 높이가 더욱 증가함을 의미한다. 이것은 그래프에서 Hi가 클수록 최대 처오름 높이 경향선 기울기가 급하게 형성되는 것을 보아 알 수 있다. 그 결과 지진해일의 파형이 가장 넓은 V/V0 = 2일 때, V/V0 = 1 대비 Hi = 3cm는 48.2%, Hi = 5cm는 58.1%, Hi = 7cm은 71.5%의 최대 처오름 높이가 증가하였다.
이상의 수치모의결과를 종합하면, 실제와 같이 넓은 파형의 지진해일이 해안으로 내습할 경우에 고립파보다 처오름 높이가 커진다. 그리고 내습하는 지진해일고가 클수록 처오름에 의한 피해는 더욱 가중될 것으로 판단된다.
4. 결론 및 고찰
본 연구에서는 고립파형 지진해일의 파형분포가 불투과 경사면 상의 처오름에 미치는 영향을 수치적으로 분석하였다. 수치모의에는 2차원 수치파동수조(Hur et al., 2011)을 이용하였고, 다양한 파형의 지진해일을 조파하기 위해 Lee et al.(2016)이 제안한 조파방법을 적용하였다. 그리고 이용하는 수치파동수조 및 지진해일 조파방법의 타당성 및 유효성을 검증하기 위하여 Synolakis(1987)의 수리모형실험에 근거한 지진해일 처오름 모의를 수행하여 실험값과 비교⋅검토하였다. 검증결과 불투과 경사면 상에서 계산의 시⋅공간파형이 실험에서 측정한 파형을 높은 정확도로 재현함을 확인하였다. 또한 수치모의를 통해 얻어진 고립파형 지진해일의 체적비에 따른 불투과 경사면 상의 처오름 특성은 다음과 같다.
(1) 고립파형 지진해일의 입사파형이 넓을수록(V/V0 가 클수록) 경사면 상의 수면형이 넓게 분포하고, 처오름이 뚜렷하게 증가하는 경향을 나타내었다.
(2) 불투과 경사면 상의 정선에서는 V/V0 가 클수록 처오름 시에 밀어주는 지속시간과 유체량이 증가하여 최대 지진해일고가 상승하였다.
(3) V/V0가 클수록 경사면 상의 유체범위가 넓어지고, 처오름 수괴의 선단 유속이 크게 증가하였다. 그리고 경사면 상에서 처오름을 증가시킬 수 있는 흐름이 넓게 분포하였다.
(4) V/V0 가 클수록 정선에서의 지진해일고가 상승하기 때문에 V/V0 가 클수록 유속의 연직분포 역시 커졌다.
(5) Hi 가 클수록 최대 처오름 높이 경향선 기울기가 급하게 형성되며, 이것은 높은 지진해일이 유입될 때 경사면 상의 처오름 높이가 더욱 증가함을 나타내는 것이다.
(6) 이상에 기인하여 파형이 가장 넓은 V/V0 = 2의 경우에서는 V/V0 = 1 대비 Hi = 3cm는 48.2%, Hi = 5cm는 58.1%, Hi = 7cm은 71.5%의 최대 처오름 높이가 증가하였다.
이상의 수치모의결과에 근거하여 실제 발생한 지진해일은 고립파 근사파형보다 넓은 파형분포를 가지기 때문에 근사이론을 적용한 지진해일 모의는 처오름 현상이 과소평가될 우려가 매우 크다. 그러므로 수리실험 또는 수치모의에서는 고립파보다 지진해일에 가까운 넓은 파형을 적용하여야 할 것이다. 나아가 불투과성 경사면 뿐 아니라, 해안지형을 고려하여 투과성 경사 해빈에 대한 지진해일 처오름 특성을 분석할 예정이다.
Acknowledgements
이 성과는 2018년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. NRF-2018R1C1B6007461).