쇄빙연구선 ARAON호의 북극해 실측 데이터에 기초한 국부 빙하중 추정식의 수정
Modification of Local Ice Load Prediction Formula Based on IBRV ARAON’s Arctic Field Data
Article information
Trans Abstract
This paper focuses on a newly designed ice load formula based on the ARAON’s 2016 Arctic field data in order to improve a structural design against ice loads. The strain gage signals from ARAON's hull plating were converted to the local ice pressure upon the hull plating using the influence coefficient matrix and finite element analysis. First, a traditional pressure-area relationship is derived by applying probabilistic approaches to handle the strains measured onboard the ARAON. Then, the local ice load prediction formula is re-analyzed after reviewing the ARAON’s additional field data to consider information about the ship speed and thickness of the sea ice. It is shown that the newly developed pressure-area relationship well reflects the influence of other design parameters such as the ship speed and ice thickness in the prediction of local ice loads on Arctic vessels.
1. 서 론
북극해와 같은 빙해역에서는 일반 해역과는 달리 해빙으로부터 유발되는 빙하중이 쇄빙선박의 가장 중요한 설계요소 중 하나이다. 하지만 빙하중은 해빙의 재료특성, 형상, 크기, 속도, 지역적인 분포 등 여러 요인에 의해 달라지므로 이를 정량적으로 파악하기는 쉽지 않다. 쇄빙선박에 작용하는 국부 빙하중은 일반적으로 해빙과의 접촉면적으로 표현되는 압력-면적 관계식(Pressure-area relationship)으로 추정하고 있다. 많은 연구자들이 다양한 조건에 대해 해양구조물 및 쇄빙선박에 대한 압력-면적 관계식을 도출한 바 있다(Masterson and Frederking, 1993; Choi and Jeong, 2008). 하지만 이러한 압력-면적 관계식은 척도효과(Scale effect)의 중요성을 강조하는 관점에서 국부 빙하중을 접촉면적 만의 간단한 함수 형태로 표현하고 있어서, 빙-구조물 상호작용에 관여되는 다른 설계변수의 영향을 전혀 고려하지 못하고 있다. 이런 이유로 국부 빙하중을 추정하는 압력-면적 관계식이 다른 주요 변수들의 영향을 포함할 수 있도록 수정되어야 할 필요성이 제기되고 있다.
본 논문에서는 쇄빙연구선 ARAON호에서 획득한 2016년 북극해 현장계측 데이터를 토대로 Frederking(2004), Jordaan et al.(1993), Taylor et al.(2010)와 같은 선행 연구에서 제시한 확률론적 접근법을 이용해 ARAON호에 대한 빙압력-접촉면적 관계식을 도출하였으며, 이후 ARAON호의 북극해 실선운항 시 계측된 선속과 해빙의 두께에 대한 정보를 추가 분석하여 앞서 도출된 압력-면적 관계식을 수정하였다. 실측 데이터에 기초하여 수정된 이 국부 빙하중 추정식은 빙압력이 단순히 접촉면적 만의 함수가 아니라 선속과 빙두께와 같은 주요 설계변수들의 영향도 받는다는 것을 잘 보여주고 있다.
2. ARAON호의 실선 계측 데이터
국내 최초의 쇄빙연구선 ARAON호는 2009년 건조되어 2010년부터 현재까지 매년 여름 북극해에서 실선시험을 수행해 왔다. 2016년 8월 북극해의 Chukchi 해와 Beaufort 해에서 있었던 실선시험에서는 이전에 드러났던 여러 미비점을 보완한 통합계측시스템을 장착하고 선체 외판에는 변형률 게이지(Strain gage)와 광섬유(Fiber optic) 센서를 부착하였고, 선체 외판의 변형률과 6자유도 선체운동 가속도, 선박의 이동속도, 해빙의 두께 등을 실시간으로 계측하였다. 그중 본 논문에서 다루는 정보는 선체 외판에서 기록된 변형률(Strains)과 선속(Ship speed) 그리고 해빙의 두께에 대한 정보이다.
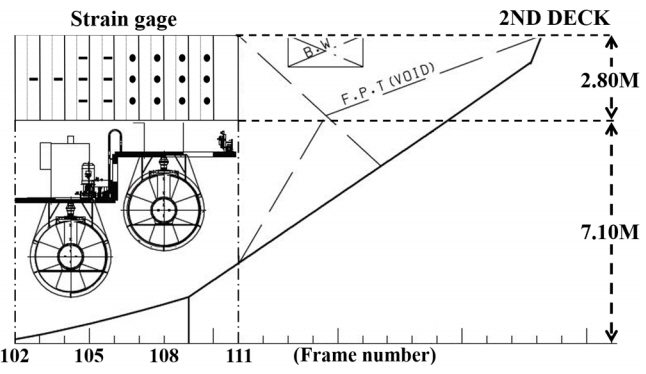
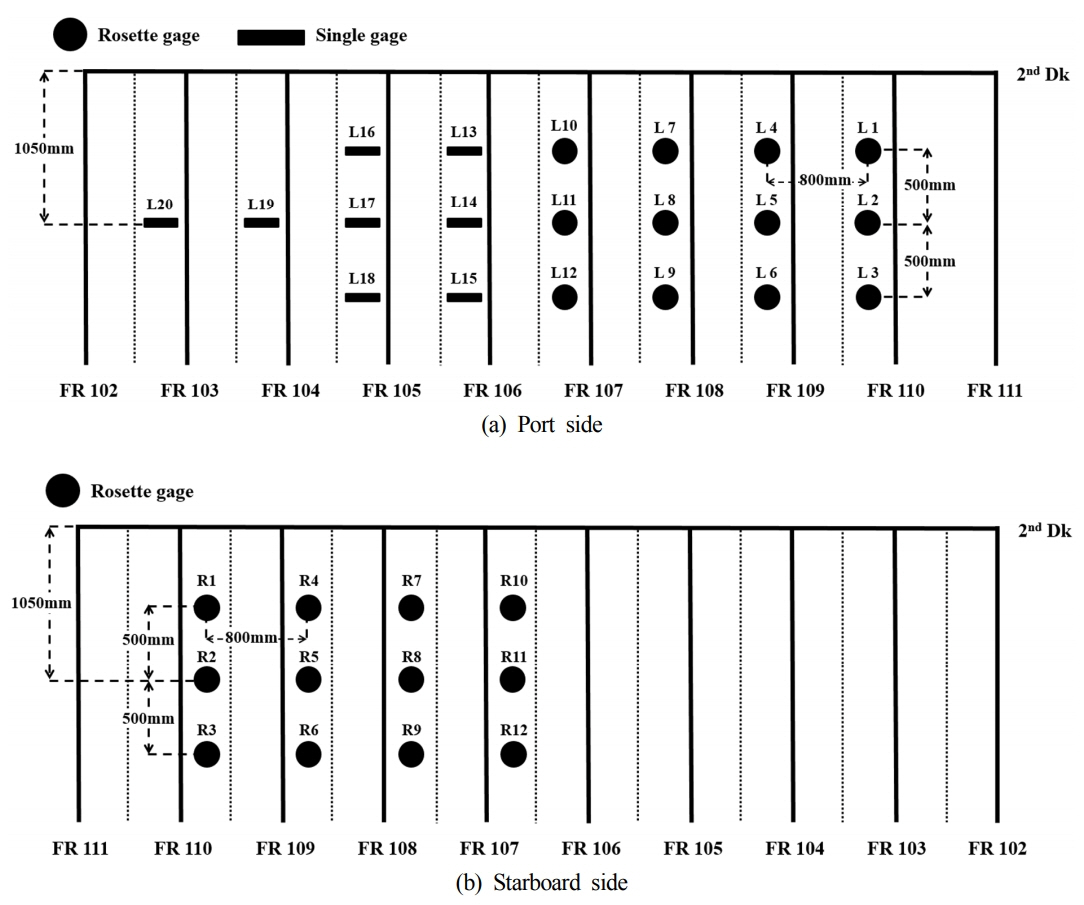
선체 외판의 변형률은 ARAON호의 선수격벽 뒤 외판 안쪽 Second deck 하부의 102번 프레임부터 110번 프레임 사이(Fig. 1)에서 계측하였다. 변형률 게이지는 좌현에 1축 게이지 8개, 로제트 게이지 20개 그리고 광섬유 센서 5세트가 설치되었으며, 우현에는 12개의 로제트 게이지가 설치되었다. 좌현에 설치된 로제트 게이지 중 8개는 전단변형률 측정을 위하여 외판이 아닌 프레임에 설치된 것이며, 5세트의 광섬유 센서는 변형률 게이지 계측치와 비교를 위한 용도로 설치된 것으로서 본 논문에서 다루는 외판부의 국부 빙하중 추정에는 좌, 우현 외판에 설치된 1축 변형률 게이지 및 로제트 게이지 데이터만 사용하고 있으며 이들의 설치 위치는 Fig. 2에 나타내었다.
변형률 게이지로부터 계측된 외판의 변형률을 외판에 발생한 응력으로 변환하는 방법은 선행 연구에서 정리된 바 있다(Kim, 2016). 선체 전후 방향이 아닌 변형률이 미치는 영향은 크지 않다는 선행 연구의 결과를 참고로 하여 1축 게이지에서 계측된 변형률을 식 (1)처럼 응력으로 변환할 수 있다. 선체 외판은 2차원 탄성체로 가정하였다.
여기서, ∊x는 선체 전후 방향 변형률, E는 외판 재료의 탄성계수를 나타낸다.
로제트 게이지에서 계측된 변형률은 다음의 식 (2), 식 (3)을 통해 계산된 주응력 σ1, σ2을 이용하여 식 (4)처럼 von Mises 등가응력으로 변환할 수 있다.
여기서 v는 포아송 비이고 ∊A, ∊B, ∊C는 로제트 게이지에서 계측된 세 방향의 변형률을 나타낸다.
이렇게 계산된 외판의 응력은 압력에 대한 영향도 행렬(Pressure influence matrix)을 이용하여 외판에 작용한 압력으로 변환할 수 있다(Lee et al., 2013). 압력 영향도 행렬은 특정한 영역에 단위 압력을 작용했을 때, 변형률 게이지가 설치된 각각의 영역에 발생하는 변형과 응력을 행렬로 만든 것으로써 유한요소법을 이용한 구조해석을 반복적으로 수행하여 구할 수 있다. 이전 시험 때와 달리 2016년 ARAON호의 실선시험에서는 변형률 게이지의 설치 위치와 담당 영역이 다르므로, 본 연구에서는 압력 영향도 행렬을 새로이 계산하였다. 압력 영향도 행렬을 계산하기 위한 구조해석은 보강재 및 프레임을 포함하여 수행되었다. 압력 영향도 행렬의 크기는 설치된 변형률 게이지의 개수에 따라 결정되며, 본 연구에서 사용된 압력 영향도 행렬의 크기는 좌현은 20×20, 우현은 12×12이다. 변형률 게이지 하나가 담당하는 영역은 800×500mm이며 좌현의 경우 20개의 변형률 게이지에 해당하는 전체 면적은 8m2, 우현의 경우 12개의 변형률 게이지에 4.8m2이 전체 면적으로 정의된다.
선박의 속도는 선체 중앙부에 GPS(Global positioning system)를 부착하여 계측하였다. 선체 우현에는 카메라를 설치하여 선수부에서 깨진 빙편이 회전하며 노출된 단면의 영상을 촬영하였다. 이 영상으로부터 Fig. 3과 같이 영상 처리 프로그램을 이용하여 빙판의 두께를 구할 수 있다(Park et al., 2014). 한편 분석에 사용된 영상은 우현 중앙부보다 조금 앞쪽에서 촬영되었고 압력은 선수부에서 계측되기 때문에, 빙두께와 압력 정보 사이에는 약간의 시간차가 있으며 본 연구에서는 실제로 설치된 센서 사이의 거리를 감안하여 데이터 기록 시간에 대한 동기화 과정을 수행하였다.

Image processing software to estimate sea ice thickness (Park et al., 2014)
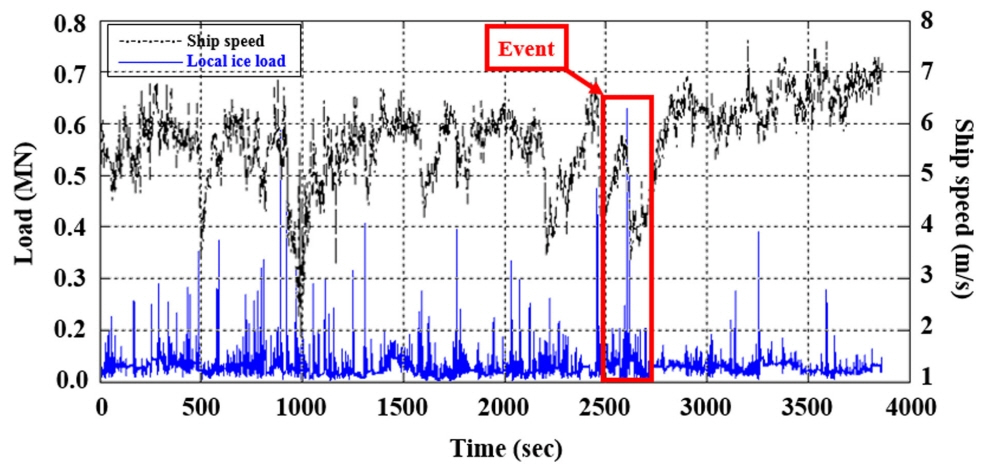
한편 이렇게 획득된 데이터 중에서 선체와 빙판과의 접촉으로 인해 발생한 실제 충격하중에 대응하는 유의미한 데이터를 얻기 위하여 선행 연구를 통해 정의된 바 있는 ‘이벤트(Event)’ 개념을 사용할 수 있다. Fig. 4는 외판 구조의 전체 계측부 면적에 대하여 계산된 빙하중과 그때 측정된 선속이 시간이 지남에 따라 변동하는 것을 나타낸 그래프이다. 이 중에서 선박의 속도가 급격히 감소하며 동시에 빙하중이 가파르게 상승하는 구간을 구별해 낼 수 있는데 이는 선체가 빙판과 충돌 시 발생하는 현상으로 볼 수 있으며, 본 연구에서는 이러한 현상 중 특정한 크기 이상의 하중이 발생한 데이터를 하나의 이벤트로 정의하였다. 이벤트에서 정의되는 최소 하중의 크기는 선행 연구의 실선 계측자료의 분석을 토대로 0.4MN으로 설정하였고 전체 실선 계측시간 중 이렇게 분류된 이벤트의 수는 총 1,712개로 분류되었다(Jeon et al., 2017).
Typical time history of calculated local ice loads and measured ship speed (Jeon et al., 2017)
3. 확률론적 접근법과 압력-면적 관계식 도출
Frederking(2004), Jordaan et al.(1993), Taylor et al.(2010)와 같은 연구자들은 확률이론을 적용한 연구를 통해 쇄빙선박에 작용하는 국부 빙하중 추정식을 도출한 바 있다. 본 연구에서는 이들이 사용한 확률론적 접근법을 2016년 ARAON호의 실선 계측 데이터에 적용하여 ARAON호에 대한 빙압력-면적 관계식을 도출하였다.
앞서 언급한 이벤트 하나에 대응하는 빙하중은 변형률 게이지 한 개에 해당하는 면적부터 좌현, 우현의 전체 면적까지 변형률 게이지 개수에 따라 조합된 여러 면적에 대해 빙압력으로 변환되었으며, 변환된 압력은 각 면적에 대해 크기순으로 정리되었다.
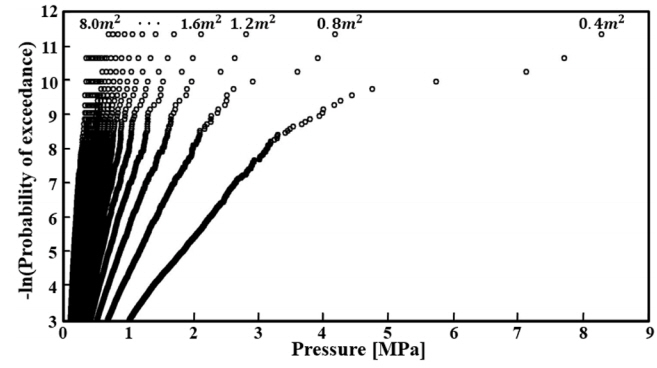
정리된 압력 데이터는 각 면적에 대해 -In(i/(n+1))으로 표현되는 Weibull plotting position을 사용하여 Fig. 5에 나타낸 것과 같이 발생한 빙압력에 대한 초과확률 그래프로 나타낼 수 있다. 여기서 i는 가장 큰 압력부터 매겨진 순위를 의미하고, n은 총 데이터 수를 의미한다.
Fig. 5를 살펴보면 각 면적에서의 초과확률의 분포 형태는 비교적 선형성을 보이는 것을 확인할 수 있다. 따라서 임의의 압력에 대한 초과확률은 데이터 관측 시간에 따라 Gumbel 분포 또는 지수 분포의 초과확률 함수를 통해 직선식의 형태로 나타낼 수 있다. 데이터 관측 시간이 매우 긴 기간일 경우 Gumbel 분포의 초과확률 함수가 데이터 분포를 잘 나타낼 수 있고, 데이터 관측 시간이 짧은 기간일 경우 지수 분포의 초과확률 함수가 데이터의 분포를 잘 나타낼 수 있다고 보고하고 있다(Jordaan et al., 1993). 2016년 ARAON호의 실선시험에서 계측된 빙하중 데이터는 비교적 짧은 시간에 계측된 것이므로 본 연구에서는 식 (5)와 같은 지수 분포의 초과확률 함수를 사용하였다.
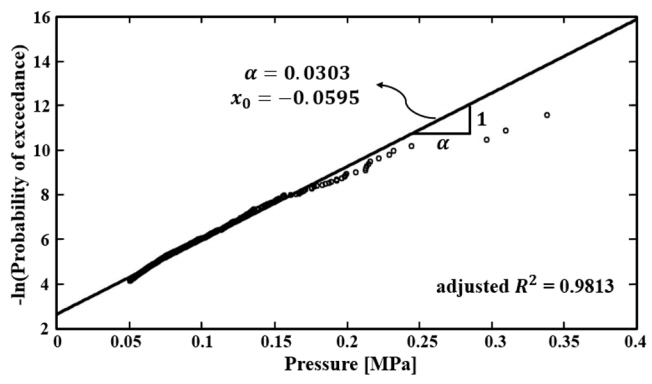
여기서, x는 임의의 압력, a는 척도모수(Scale parameter), xo 는 위치모수(Location parameter)를 의미한다. a와 xo 는 Fig. 6과 같이 데이터 분포 형태에 따른 직선의 기울기와 절편으로 결정할 수 있다.
Determination of constants α and x0 from fit to tail of peak ice pressure distribution for area 8 m2
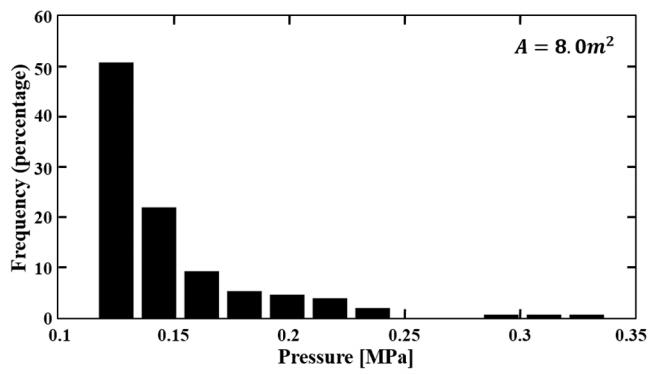
계측된 압력 데이터가 실제로 식 (5)와 같은 지수 분포를 따르는지 검증하기 위해 Anderson-Darling 법을 이용한 적합도(Goodness-of-fit) 검정을 수행하였으며, 모든 면적에서의 압력 데이터 분포는 95%의 신뢰수준에서 지수 분포가 적합함을 보여 주었다. Fig. 7은 8m2의 면적에 해당하는 ARAON호의 압력 데이터 분포를 나타낸 것이며, 이를 살펴보면 데이터 분포 형태가 지수 분포의 형태인 것을 볼 수 있다.
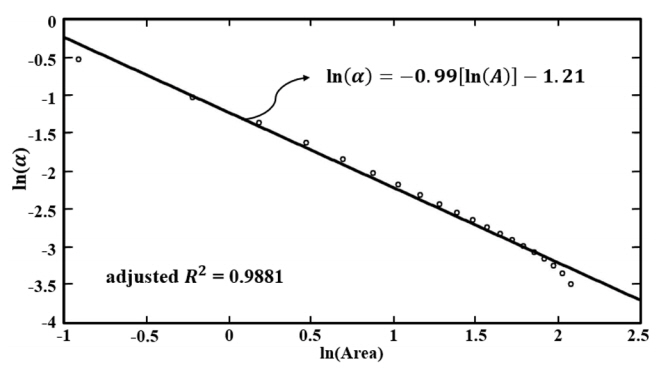
xo가 음수 또는 0에 가까울 경우 초과확률에 대한 변수의 영향은 무시할 수 있으며(Taylor et al., 2010), 본 연구에서는 모든 면적에 대해 xo 가 음수로 계산된다(Fig. 6). Fig. 8은 모든 면적에 대하여 결정된 α를 로그-로그 그래프로 나타낸 것이다. α의 분포 형태에 따른 하나의 직선식을 찾아낼 수 있으며 이때의 기울기와 절편을 통해 α는 식 (6)과 같이 면적에 대한 지수 함수로 나타낼 수 있다.
각각의 데이터는 서로 연관성이 없는 독립성(Independence)을 가지고, 매우 짧은 시간에서 동시에 여러 개의 충돌이 발생할 확률은 무시할 수 있을 만큼 작다. 따라서 단위 시간당 발생하는 최대 압력을 P라 하면 P가 발생할 초과확률 FP(p)은 식 (7)과 같이 단위 기간 동안 발생하는 총 이벤트 수 μ와 식 (5)의 초과확률함수의 곱을 모수로 하는 포아송 과정의 초과확률 함수로 나타낼 수 있다(Taylor et al., 2010).
식 (7)에 식 (6)의 α를 대입하여 식 (8)과 같이 국부 빙압력 p을 추산할 수 있다.
ARAON호의 2016년 실선시험에서 총 계측시간은 약 310시간이고 이때 발생한 이벤트는 총 1,712개 이므로 이벤트는 평균적으로 시간당 5.5개가 발생하였다. ARAON호가 1년 동안 약 1,000시간을 운항한다고 가정하면 1년 동안 평균적으로 발생 가능한 이벤트의 개수는 5,523개이다. 따라서 초과확률에 따른 빙압력은 식 (9)와 같이 정리된다.
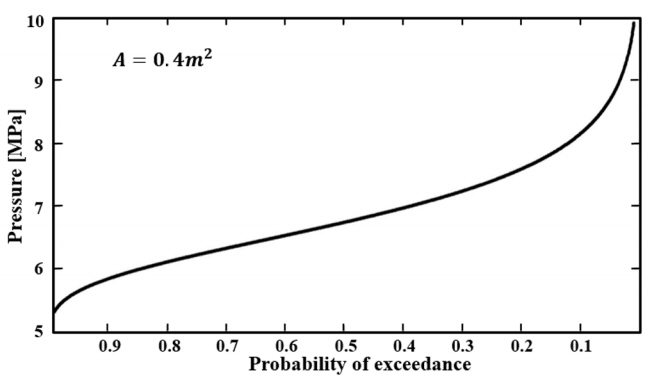
Fig. 9는 초과확률에 따라 발생 가능한 특정 면적에서의 최대빙압력을 그래프로 나타낸 것이다.
설계압력에 대해서 1%의 초과확률에 해당하는 압력은 선박의 치명적인 것은 아니지만 외판이 찌그러지는 손상을 주는 정도의 압력으로 여러 연구에서 1%의 초과확률에 해당하는 압력을 선택하고 있다(Frederking, 2003). ARAON호의 2016년 실선시험을 토대로 1%의 초과확률에 대한 국부 빙압력 추정식은 식 (10)와 같은 압력-면적 관계식으로 나타낼 수 있다.
4. 선속과 빙두께를 고려한 압력-면적 관계식 수정
빙압력과 얼음과의 접촉면적 사이의 관계식 (10)은 접촉면적만의 함수로 매우 간단하게 표현되어 있다. 식 (10)은 ARAON호와 비슷한 크기의 쇄빙선박의 국부 빙하중 추정에 초기 계산으로 사용할 수 있지만 접촉면적 외에 다른 설계요소의 영향은 전혀 파악할 수 없다는 문제가 있다. 이런 이유로 주요 설계요소인 선속과 빙두께의 변화에 따른 국부 빙하중 추정식을 새롭게 도출할 필요가 있다. 본 연구에서는 ARAON호의 2016 실선 시험에서 획득한 선속과 빙두께에 대한 정보를 각 이벤트에서의 빙압력 분포와 연결하는 방법으로 접근하였다.
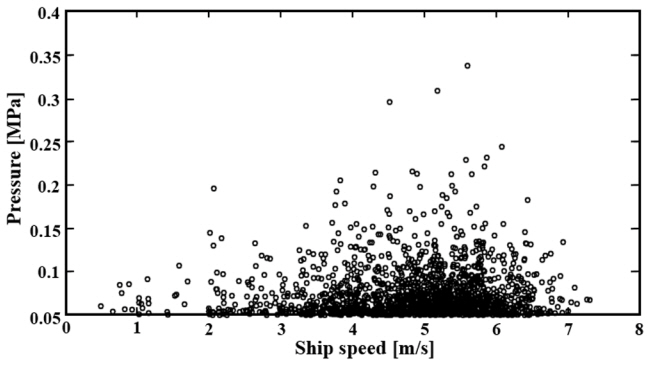
Fig. 10은 빙압력 데이터 분포를 선속에 대한 그래프로 나타낸 것이다. 이를 살펴보면 빙압력 데이터는 넓은 선속 구간에 걸쳐 분산되어 있지만, 선속이 증가함에 따라 빙압력이 증가하는 경향을 알 수 있다. 빙압력에 미치는 선속의 영향을 반영하기 위하여 Fig. 10에 나타난 데이터 분포를 무차원 속도 변수 Froude 수를 사용하여 재분석하였다.
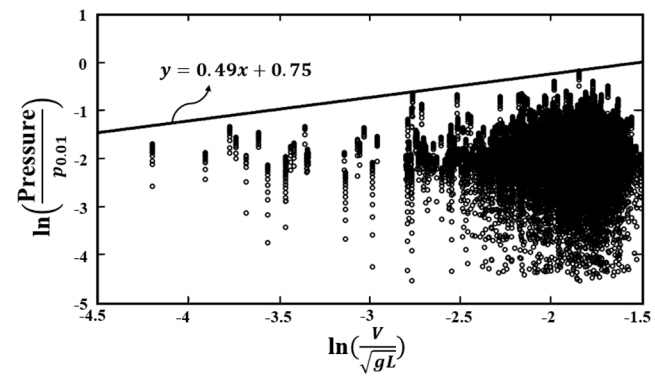
여기서, V는 선박의 속도, g는 중력가속도, L은 선박의 특성길이를 의미하며 ARAON호에 대하여 110m를 사용하였다. Fig. 11은 이렇게 정의된 Froude 수에 대해 무차원화된 빙압력 데이터를 로그-로그 그래프로 나타낸 것이다. 빙압력 데이터의 최대값을 넘지 않도록 식 (12)와 같은 직선식을 찾을 수 있으며 이를 이용해 기존의 압력-면적 관계식 (10)에서 식 (13)과 같이 선속을 포함하는 새로운 국부 빙하중 추정식으로 수정할 수 있다.
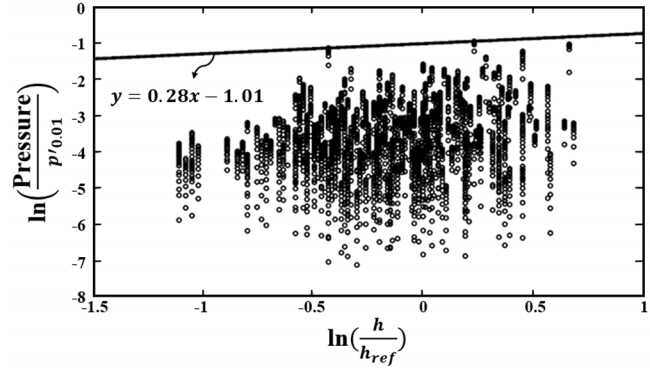
마찬가지 방법으로 해빙의 두께를 고려한 빙압력 추정식을 유도할 수 있다. 해빙의 두께에 따른 최대 빙압력 데이터 분포는 선속의 변화에 따른 빙압력의 분포만큼 넓은 범위에 걸쳐 분산되어 있고 빙두께가 증가함에 따라 최대 빙압력 또한 증가하는 경향이 있지만, 그 정도는 선속의 영향에 비해 그다지 심하지는 않다. 기존의 추정식에 해빙의 두께를 고려하기 위하여 기준 두께에 대한 해빙의 두께로 정의하는 무차원 변수 h/href를 이용하였다. 여기서, href는 1m의 기준 두께를 의미한다.
Fig. 12는 해빙의 두께에 대해 무차원화된 빙압력 데이터를 로그-로그 그래프로 나타낸 것이다. 빙압력 데이터의 최대값을 넘지 않도록 식 (14)와 같은 직선식을 찾을 수 있다.
한편 해빙의 두께 정보는 전체 빙압력 데이터 중 일부에 대해서만 획득했기 때문에 본 연구에서는 그중 최대 두께에 해당하는 1.98m에서 최대 빙압력이 발생했다고 가정하여 식 (14)을 식 (15)와 같이 수정하였다. 이를 통해 기존의 압력-면적 관계식은 식 (16)와 같이 선속과 빙두께를 고려한 국부 빙하중 추정식으로 수정되었다.
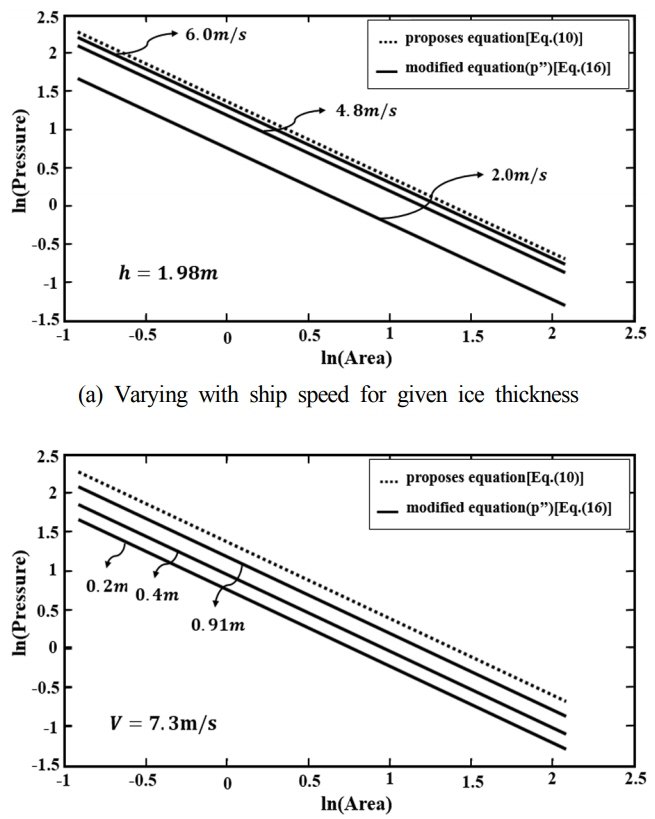
Fig. 13은 새롭게 도출된 국부 빙하중 추정식 (16)을 기존 빙압력-면적 관계식과 함께 로그-로그 그래프에서 비교한 것이다. 새로운 추정식 (16)은 접촉면적 만을 고려하는 기존의 추정식 (10)과 달리 충돌 시 선박의 속도와 해빙의 두께에 따른 최대빙압력의 변화를 명확하게 보여주고 있다.
5. 결 론
본 논문에서는 쇄빙연구선 ARAON호에서 획득한 2016년 북극해 현장계측 데이터를 토대로 확률론적 접근법을 이용해 ARAON호에 대한 압력-면적 관계식 (10)을 도출하였으며, 이후 ARAON호의 북극해 실선운항 시 계측된 선속과 해빙의 두께에 대한 정보를 추가적으로 분석하여 앞서 도출된 압력-면적 관계식을 수정한 식 (16)을 도출하였다. 실측 데이터에 기초하여 수정된 국부 빙하중 추정식 (16)은 빙압력이 단순히 접촉면적 만의 함수가 아니라 선속과 빙두께와 같은 주요 설계요소의 영향을 받는다는 것을 잘 보여주고 있다. 이 국부 빙하중 추정식은 ARAON호와 유사한 규모의 쇄빙선박에 대한 초기 빙하중 추정에 사용할 수 있으며 향후 계측 데이터를 확보할 수 있다면 규모가 다른 쇄빙선박에도 보완 적용될 수 있을 것이다.
Acknowledgements
본 연구는 산업통상자원부 지원 산업핵심기술과제 ‘ARC7 극지환경용 해양플랜트 내빙구조 설계기술 개발’과제(과제번호 10063417)의 연구비 지원으로 수행된 결과임.