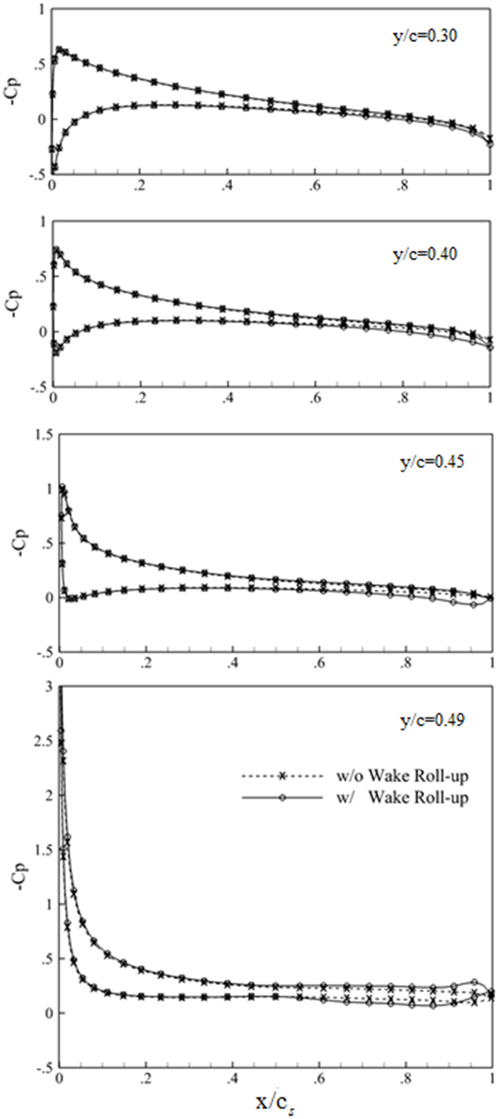
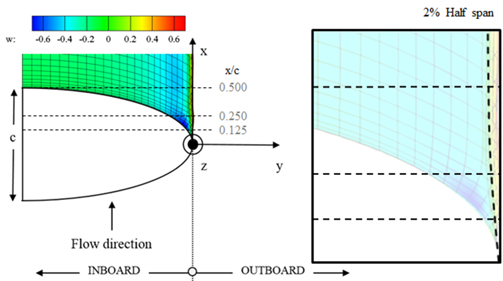
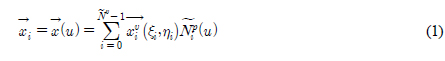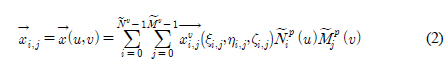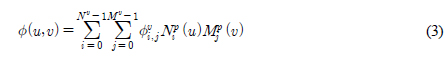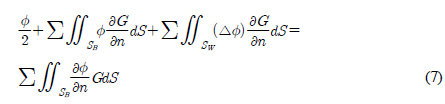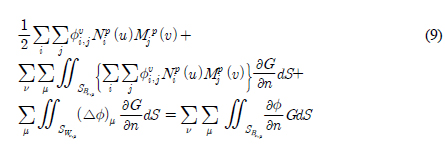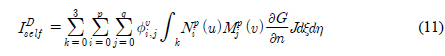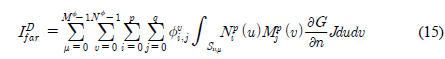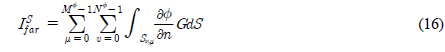Ahn, B.K., Kim, G.D., Lee, C.S.. (Wake Roll-up Modeling and Steady Hydrodynamic Analysis of Marine Propellers Using a B-Spline Based Higher-Order Panel Method, Journal of the Society of Naval Architects of Korea, 2008). 45, 353-360 10.3744/SNAK.2008.45.4.353.


Arndt, R.E.A., Arakeri, V.H., Higuchi, H.. (Some Observations of Tip-vortex Cavitation, Journal of Fluid Mechanics, 1991). 229, 269-289 10.1017/S0022112091003026.

Astolfi, J.A., Fruman, D.H., Billard, J.Y.. (A Model for Tip Vortex Roll-up in the near Field Region of Three-dimensional Foils and the Prediction of Cavitation Onset, European Journal of Mechanics-B/Fluids, 1999). 18(4):757-775 10.1016/S0997-7546(99)00101-6.

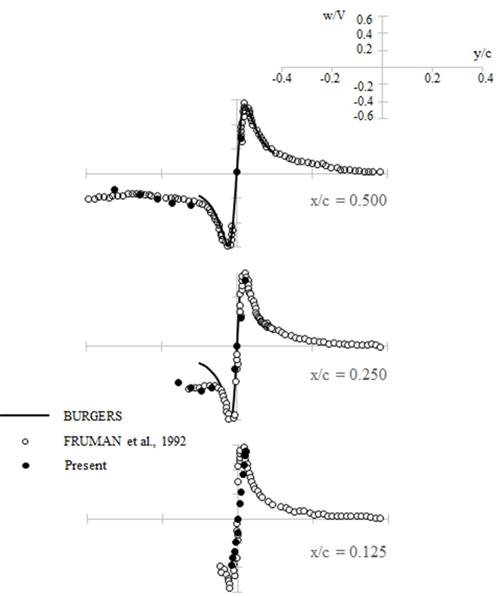
Fruman, D.H., Dugue, C., Pauchet, A., Cerrutti, P., Briancon-Marjolet, L.. (Tip Vortex Roll-Up and Cavitation Proceedings of 9th Symposium on Naval Hydrodynamics Seoul, Korea: 1992.
Hsin, C.Y., Kerwin, J.E., Newman, J.N.. (A Higher-order Panel Method Based on B-splines Proceedings of 6th International Conference on Numerical Ship Hydrodynamics USA: 1993.
Kim, G.D., Hwang, U.S., Lee, C.S.. (A B-Spline Higher Order Panel Method for Analysis of Three Dimensional Potential Flow, Journal of the Society of Naval Architects of Korea, 2000). 37(2):57-69.
Kim, G.D., Lee, C.S.. (Application of High Order Panel Methd for Improvement of Prediction of Marine Propeller Performance, Journal of the Society of Naval Architects of Korea, 2005). 42(2):113-123 10.3744/SNAK.2005.42.2.113.


Kim, G.D., Lee, C.S., Kerwin, J.E.. (A B-spline Based Higher Order Panel Method for Analysis of Steady Flow around Marine Propellers, Ocean Engineering, 2007). 34(14):2045-2060 10.1016/j.oceaneng.2007.02.013.

Kinnas, S.A., Lee, H.S., Mueller, A.C.. (Prediction of Propeller Blade Sheet and Developed Tip Vortex Cavitation 22nd Symposium on Naval Hydrodynamics Washington DC USA: 1998). 182-198.
Kuiper, G.. (New Developments around Sheet and Tip Vortex Cavitation on Ship Propellers 4th International Symposium on Cavitation, California Institute of Technology Pasadena USA: 2001). lecture.007.
Lee, H.S., Kinnas, S.A.. (Modeling of Unsteady Blade Sheet and Developed Tip Vortex Cavitation 4th International Symposium on Cavitation California, USA: 2001.
Lee, C.S., Kerwin, J.E.. (A B-spline Higher Order Panel Method Applied to Two-dimensional Lifting Problem, Journal of Ship Research, 2003). 47(4):290-298.


Lee, C.S., Kim, G.D., Kerwin, J. E.. (A B-spline Based Higher Order Panel Method for Analysis of Steady Flow around Marine Propellers Proceedings of 25th Symposium on Naval Hydrodynamics Canada: 2004.
Maines, B.H., Arndt, R.E.A.. (Tip Vortex Formation and Cavitation, Journal of Fluid Engineering, 1997). 119, 413-419 10.1115/1.2819149.

Maniar, H. D.. (A Three Dimensional Higher Order Panel Method Based on B-spline, Doctoral Dissertation Massachusetts Institute of Technology; 1995.
McCormick, B.W.. (On Cavitation Produced by a Vortex Trailing From a Lifting Surface, Journal of Basic Engineering, 1962). 84, 369-378 10.1115/1.3657328.

Piegl, L., Tiler, W.. (The NURBS Book 2nd Edition Springer-Verlag, 1996.
Pyo, S., Kinnas, S.A.. (Propeller Wake Sheet Roll-up Modeling in Three Dimensions, Journal of Ship Research, 1997). 41(2):81-92.


Souder, W.G., Platzer, G.P.. (Tip Vortex Cavitation Characteristics and Delay of Inception on a Three Dimensional Hydrofoil. Ship Performance Development Research and Development Report 1981.
Suciu, E.O., Morino, M.. (Nonlinear Finite-element Analysis of Wings in Steady Incompressible Flows with Wake Roll-up. American Institute of Aeronautics and Astronautics(AIAA) paper 1976.
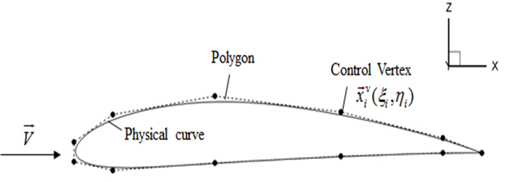
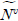 نè¤ ندجم░£ن│هêء م│╡م░هùه£ م╕░وـءوـآهب هب£هû┤هب(Control vertex)هإ╕
نè¤ ندجم░£ن│هêء م│╡م░هùه£ م╕░وـءوـآهب هب£هû┤هب(Control vertex)هإ╕ 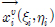 هإء م░£هêءهإ┤نر░,
هإء م░£هêءهإ┤نر░, 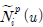 نè¤ B-هèجو¤îنإ╝هإ╕هإ هإ┤هأروـ£ وّ£وءم╕░ن▓ـهùه£ م░هجّوـذهêء(Weight function) هùصوـبهإ وـءنè¤ p-ه░ذ م╕░هبوـذهêءهإ┤نïج(Fig. 1). هإ┤نح╝ 3ه░ذهؤه£╝نة£ وآـهئحوـءنر┤ ندجم░£ن│هêء (u, v)هù نîوـءهùش هïإ (2)هآ م░آهإ┤ وّ£وءوـب هêء هئêنïج.
نè¤ B-هèجو¤îنإ╝هإ╕هإ هإ┤هأروـ£ وّ£وءم╕░ن▓ـهùه£ م░هجّوـذهêء(Weight function) هùصوـبهإ وـءنè¤ p-ه░ذ م╕░هبوـذهêءهإ┤نïج(Fig. 1). هإ┤نح╝ 3ه░ذهؤه£╝نة£ وآـهئحوـءنر┤ ندجم░£ن│هêء (u, v)هù نîوـءهùش هïإ (2)هآ م░آهإ┤ وّ£وءوـب هêء هئêنïج.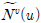 هآ
هآ 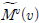 نè¤ ندجم░£ن│هêء م│╡م░هùه£هإء م╕░وـءوـآهب هب£هû┤هبهإ╕
نè¤ ندجم░£ن│هêء م│╡م░هùه£هإء م╕░وـءوـآهب هب£هû┤هبهإ╕ 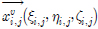 هإء م░£هêءهإ┤نر░
هإء م░£هêءهإ┤نر░ 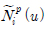 هآ
هآ 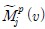 نè¤ p-ه░ذ م╕░هبوـذهêءهإ┤نïج. نءوـ£ نآهإ╝وـ£ م╕░ن▓ـه£╝نة£ ندجم░£ن│هêء(u, v)هù نîوـءهùش 3ه░ذهؤ م│╡م░هùه£هإء هنوشوàهà£هإ هïإ (3)م│╝ م░آهإ┤ وّ£وءوـب هêء هئêنïج.
نè¤ p-ه░ذ م╕░هبوـذهêءهإ┤نïج. نءوـ£ نآهإ╝وـ£ م╕░ن▓ـه£╝نة£ ندجم░£ن│هêء(u, v)هù نîوـءهùش 3ه░ذهؤ م│╡م░هùه£هإء هنوشوàهà£هإ هïإ (3)م│╝ م░آهإ┤ وّ£وءوـب هêء هئêنïج.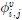 )هإء م░£هêءهإ┤نر░, م╕░وـءوـآهب هب£هû┤هبم│╝ هنوشوàه࣠هب£هû┤هبهإ نآهإ╝وـب وـهأ¤م░ هùنïج. نءوـ£
)هإء م░£هêءهإ┤نر░, م╕░وـءوـآهب هب£هû┤هبم│╝ هنوشوàه࣠هب£هû┤هبهإ نآهإ╝وـب وـهأ¤م░ هùنïج. نءوـ£ 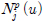 هآ
هآ  نè¤ هنوشوàهà£هإء وّ£وءهإ ه£وـ£ B-هèجو¤îنإ╝هإ╕ م╕░هبوـذهêءهإ┤نïج.
نè¤ هنوشوàهà£هإء وّ£وءهإ ه£وـ£ B-هèجو¤îنإ╝هإ╕ م╕░هبوـذهêءهإ┤نïج.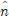 هإ نش╝ه▓┤وّ£نر┤هùه£ ه£بنآهئح ن░روûحه£╝نة£هإء هêءهدن░روûح نïذه£ن▓ةو░,
هإ نش╝ه▓┤وّ£نر┤هùه£ ه£بنآهئح ن░روûحه£╝نة£هإء هêءهدن░روûح نïذه£ن▓ةو░, 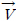 نè¤ ه£بنآهئح هننح╝ نéءوâنé╕نïج.
نè¤ ه£بنآهئح هننح╝ نéءوâنé╕نïج.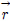 هإ هب£هû┤هبم│╝ وè╣هإ┤هب هéشهإ┤هإء م▒░نخش ن▓ةو░هإ┤نïج.
هإ هب£هû┤هبم│╝ وè╣هإ┤هب هéشهإ┤هإء م▒░نخش ن▓ةو░هإ┤نïج.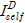 ,
, 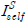 )هإ نïجهإî هïإ (11), (12)هآ م░آهإ┤ نéءوâنé╝ هêء هئêنïج.
)هإ نïجهإî هïإ (11), (12)هآ م░آهإ┤ نéءوâنé╝ هêء هئêنïج.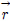 هإ هب£هû┤هبهùه£ وîذن ه£هإء وè╣هإ┤هبهù هإ┤نح┤نè¤ م▒░نخش ن▓ةو░نة£ B-هèجو¤îنإ╝هإ╕ وàه£م│▒هإء م╕ëهêءنة£ وّ£وءن£نïج. نءوـ£ هب£هû┤هبهإ┤ نش╝ه▓┤ وّ£نر┤هùه£ نرنخش نûذهû┤هب╕ هئêنè¤ م▓╜هأ░هùنè¤ ندجم░£ن│هêء م│╡م░هùه£ هدهبّ هؤهئح م╖╝هéشن▓ـهإ هéشهأروـءهùش م│هé░وـءهءنïج. هؤم▒░نخشهإء ه▓آنم░ نءنè¤ هؤهئحم╕░هجهإ نïجهإî هïإ (14)هآ م░آهإ┤ هبـهإءنءنر░, هإ┤نح╝ ندîهة▒وـءهد هـèه£╝نر┤ هة░م▒┤هù ندîهة▒وـب نـî م╣îهد وîذنهإ ن╢وـبوـءهùش هبن╢وـ£نïج.
هإ هب£هû┤هبهùه£ وîذن ه£هإء وè╣هإ┤هبهù هإ┤نح┤نè¤ م▒░نخش ن▓ةو░نة£ B-هèجو¤îنإ╝هإ╕ وàه£م│▒هإء م╕ëهêءنة£ وّ£وءن£نïج. نءوـ£ هب£هû┤هبهإ┤ نش╝ه▓┤ وّ£نر┤هùه£ نرنخش نûذهû┤هب╕ هئêنè¤ م▓╜هأ░هùنè¤ ندجم░£ن│هêء م│╡م░هùه£ هدهبّ هؤهئح م╖╝هéشن▓ـهإ هéشهأروـءهùش م│هé░وـءهءنïج. هؤم▒░نخشهإء ه▓آنم░ نءنè¤ هؤهئحم╕░هجهإ نïجهإî هïإ (14)هآ م░آهإ┤ هبـهإءنءنر░, هإ┤نح╝ ندîهة▒وـءهد هـèه£╝نر┤ هة░م▒┤هù ندîهة▒وـب نـî م╣îهد وîذنهإ ن╢وـبوـءهùش هبن╢وـ£نïج.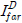 ,
, 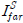 )هإ نïجهإî هïإ (15), (16)م│╝ م░آنïج(Kim et al., 2000).
)هإ نïجهإî هïإ (15), (16)م│╝ م░آنïج(Kim et al., 2000).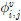 )هإء هبوءـ هجّه▓ره£╝نة£ وّ£وءوـب هêء هئêنïج.
)هإء هبوءـ هجّه▓ره£╝نة£ وّ£وءوـب هêء هئêنïج.