3차원 수치파동수조에서 수중발파에 의한 수면파의 전파해석
Water Wave Propagation Caused by Underwater Blasting in a 3D Numerical Wave Tank
Article information
Trans Abstract
When underwater blasting is conducted, both shock waves and water waves have an effect on adjacent coastal areas. In this study, an empirical formula for estimating the details of water waves caused by underwater blasting was applied to a non-reflected wave generation system, and a 3D numerical wave tank (NWT) was improved to reproduce the generation and propagation of such water waves. The maximum elevations of the propagated water waves were comparatively analyzed to determine the validity and effectiveness of the NWT. Good agreement was demonstrated between the empirical and simulation results. The generation and propagation of water waves were also simulated under each underwater blasting scenario for the removal of the Todo islet at the Busan Newport International Terminal (PNIT). It was determined that the water waves generated by the underwater blasting scenario examined in this study did not have a significant impact on the PNIT. In addition, multiple-charge blasting caused higher wave heights than single-charge blasting. As the amount of firing charge increased, the wave height also increased. Finally, larger water waves were generated during the later blasting conducted at a deeper depth as compared with an earlier blasting conducted at a relatively shallow depth.
1. 서 론
수중발파는 일반적으로 부피가 큰 수중의 구조물/장애물을 철거하는 과정에 필요한 공정이다. 해양개발이 지속적으로 진행됨에 따라 수중발파 또한 증가하는 추세이다. 그리고 해안 및 항만 공사에서는 대규모의 수중발파가 수반되는 경우가 많다. 대표적 예로서 부산신항만에서는 선박의 입⋅출항에 걸림돌이 되어온 토도를 제거하기 위해 수중발파를 동반한 공사가 진행되고 있다. 해양수산부는 2018년부터 2020년까지 국비 3,437억원을 투입하여 부산신항만의 선반 운항의 안전과 항만 운용의 효율성을 높이기 위해 토도 제거를 추진하며, 수심 -17m를 확보할 예정이다.
Fig. 1처럼 수중폭파는 공기 중 폭발과 같이 순간적으로 발생하며, 고압의 충격파가 수중에서 빠른 속도로 전파된다. 수중에서는 공기보다 압력전파속도가 빠르고, 발생한 가스 또는 에너지가 소실 전에 물에 의해 기포 형태로 갇히게 된다(Choi et al. 2017). 충격파는 기포 크기가 최소일 때 발생하고, 이 기포는 외부 압력과 중력의 영향으로 팽창과 수축을 반복하며, 수면으로 상승하게 된다(Hunter and Geers, 2002; Klaseboer et al., 2005; Hamashima et al., 2010). 이러한 일련의 과정이 수중폭파지점을 기점으로 한 수면파동을 발생시키고, 주변 해역까지 영향을 미치게 된다. 그러므로 가동 중인 부산신항만에서 수행하는 토도 제거를 위한 수중발파의 수면파동이 컨테이너 터미널에 미치는 영향을 면밀하게 검토할 필요가 있다.
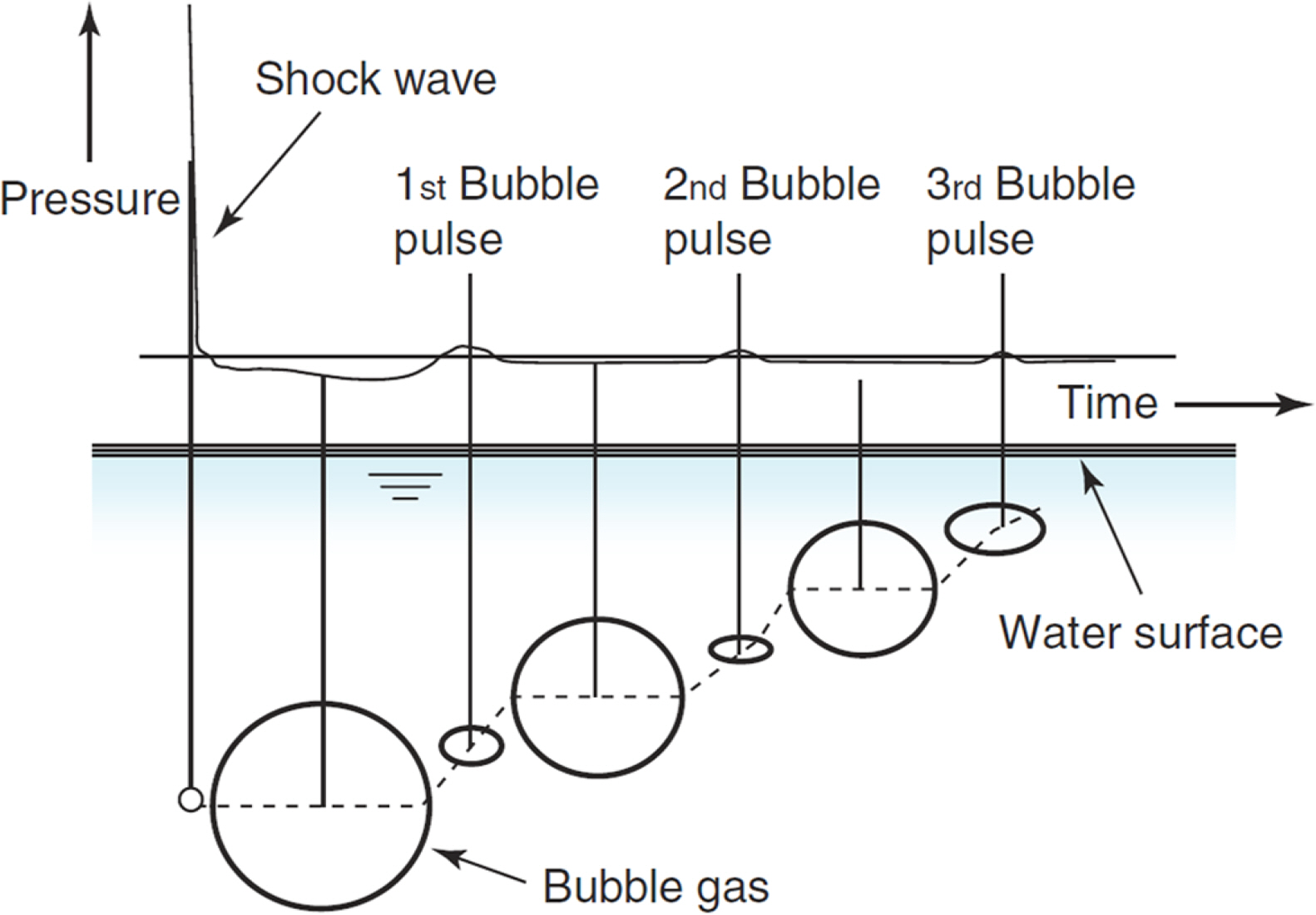
Schematic illustration of underwater explosion phenomenon (Hamashima et al., 2010)
수중폭파에 관한 연구들은 대부분 충격파의 물리적 특성을 분석(Cole, 1948; Costanzo, 2011)에 중점을 두고, 충격파가 주변 구조물(Zhang et al., 2017; Saadatfar and Zahmatkesh, 2018), 선박(Warren, 1996; Ming et al., 2016), 생태계(Keevin and Hempen, 1997; Govoni et al., 2008)에 미치는 영향을 분석 또는 모니터링(Carlson et al., 2011)을 수행하였다. 이에 반해 수면파의 발생 및 전파에 관한 연구들은 아직까지 미진한 실정이다. 국내에서는 수중발파 사례분석에 관한 연구(Jeung et al., 2004; An et al., 2007; Kim and Kim, 2018)가 주로 수행되었다. 그리고 수중발파현장에서 측정한 자료로부터 진동추정식을 제안하였다(Park et al., 2006). 수중발파에 대한 어류 및 구조물의 영향평가(Lee et al., 2001; Choi et al., 2015)에 관한 연구도 수행되었다.
최근에서는 CFD(Computational fluid dynamics) 기반의 수치해석에서 수중폭파에 의한 수면파동이 계산되기도 한다. Miller et al.(2013)은 유한 체적법의 이상류 해석으로부터 수중폭파 시에 압력강하에 의한 동공현상, 기포 상승, 수면파 생성에 관한 수치해석을 수행하기도 하였으나, 수면파 전파과정에 관한 검토는 수행되지 않았다. Wang et al.(2014)의 다상류 해석에서는 충격파와 공동현상에 의한 수면파동이 발생하나, 이것에 대한 논의가 이루어지지 않았다. 현실적으로 수중폭파부터 수면파동의 발생과 전파까지 직접 모의하기에는 많은 어려움이 따른다. 한편 Le Méhauté and Wang(1996)은 수중발파 시에 TNT(Trinitrotoluene) 장약량에 따른 최대수위, 수면파의 주기 등에 관한 경험식을 제안하였다. 이 경험식을 이용하여 수중폭발에 따른 수면파의 발생과 전파를 해석한다면, 전술한 이상류 또는 다상류 수치모델이 아닌 단상류 수치모델에서도 시뮬레이션이 가능할 것이다.
본 연구에서는 Navier-Stokes(N-S) 방정식에 기반의 단상류 수치모델 LES-WASS-3D Ver. 2.0(Lee and Hur, 2014a)을 이용한다. 그리고 Le Méhauté and Wang(1996)의 추정식을 무반사 조파시스템에 적용하는 방법을 제안한다. 나아가 부산신항만의 토도 제거를 위한 수중발파 시나리오별 수면파의 발생과 전파에 관한 3차원 시뮬레이션을 수행하여 주변 컨테이너 및 다목적 터미널에 미치는 영향을 분석한다.
2. 수치모델
본 연구에서는 수중발파에 의한 수면파의 3차원적 전파특성을 분석하기 위하여 LES-WASS-3D ver. 2.0(Lee and Hur, 2014a)을 이용한다. 이 3차원 수치파동수조는 PBM(Porous body model)과 VOF(Volume of fluid)를 토대로 개량된 3-D N-S Solver의 강비선형 모델이다. 그리고 무반사 조파시스템에 의해 파와 흐름을 자유자재로 생성할 수 있다. 아격자 규모의 난류해석을 위해 Smagorinsky(1963)에 기초한 Germano et al.(1991)과 Lilly(1992)의 동적 와동점성모델, 자유수면의 표면장력을 고려하기 위해 Brackbill et al.(1992)의 CSF(Continuum surface force)모델을 수치파동수조에 각각 도입하였다.
2.1 지배방정식
지배방정식은 비압축성⋅점성유체에서 무반사로 파 또는 흐름을 생성할 수 있게 조파원천이 포함된 연속방정식 (1)과 PBM을 토대로 질량 및 에너지 보전, 투수매체에 의한 에너지 소산을 정량적으로 계산할 수 있게 수정된 N-S 운동량 방정식 (2)로 구성된다.
여기서 vi는 x, y, z방향의 유속성분, q*는 소스의 유량밀도, γv는 체적공극률, γi는 x, y, z방향의 면적투과율, t는 시간, ρ는 수온과 염분을 고려한 물의 밀도, p는 압력, vT는 수온과 염분에 따른 물의 동점성계수(v)와 동적 난류모델에서 구한 와동점성계수(vt)의 합, Dij는 변형률속도텐서, Si는 CSF모델에 의한 표면장력항, Qi는 조파원천항, Ri는 투과매체의 유체저항항, gi는 중력가속도항, Ei는 에너지 감쇠항을 각각 나타낸다.
F는 각 계산 격자에서 유체의 체적비를 나타내고, 비압축성 유체에 대한 가정과 PBM을 적용하여 VOF 함수를 유체의 보존형식으로 나타내면 다음과 같다.
세부적인 수치해석방법에 대해서는 Hur et al.(2012)과 Lee and Hur(2014a), Lee and Hur(2014b)를 참조하기 바란다.
2.2 조파방법
2.2.1 수면파형
수중폭파에 발생하는 수면파형은 크노이드파 형태를 가진다(Le Méhauté and Wang, 1996), 본 연구에서는 수중폭파에 의한 수면파는 단파임을 감안하여 크노이드파를 대신한 비주기성의 고립파를 적용한다. 이에 Le Méhauté and Wang(1996)는 실험을 통해 천해역에서 TNT 장약량에 따른 최대수위, 수면파의 주기 등에 관한 경험식을 이용하며, Fig. 2처럼 수중폭파 시에 생성되는 고립파형의 수면파 제원을 식 (4)-(6)들로부터 얻을 수 있다.
여기서 ηmax는 최대수위, r은 발파지점으로부터의 수평거리, W는 TNT 기준 장약량, α와 β는 식 (7)-(8)과 같은 경험계수, CW 식 (9)과 같은 경험계수, R은 초기 수면형의 반경, T는 주기, h는 수심, z는 발파 수심을 각각 나타낸다. 여기서 단위는 ft와 lb이다.
본 연구에서는 이 경험식에서 산정되는 수면파의 제원을 무반사 조파시스템에 적용하여 수면파의 생성과 전파를 모의한다.
2.2.2 조파방법
양방향으로 파랑이 생성되는 방식(Brorsen and Larsen, 1987)을 개량하여 수치파동수조의 4방향(x의 ±방향, y의 ±방향)으로 수면파를 전파될 수 있게 조파원천을 개량하였으며, 식 (10)과 같이 4배의 조파강도(q)를 가진다. 그리고 수치파동수조 내의 장애물 또는 경계로부터 발생하는 반사파의 영향을 최소화하기 위하여 Ohyama and Nadaoka(1991)가 제안한 강도조절계수(ζ)을 적용하여 안정적으로 수면파를 생성한다.
여기서 V0는 수면파의 수평 유속성분, ζ는 강도조절계수(η0+h/ηs+h), η0는 이론적 수면 변위, ηs는 실제 수면 변위)이다.
엇갈림 격자체계를 채택한 수치모델에서는 격자 크기에 따른 q의 영향을 배제할 필요가 있다. 본 연구에서는 식 (11)처럼 격자 크기의 영향이 없는 유량밀도(q*)를 지배방정식에 대입한다. 그리고 단일발파의 조파영역은 하나의 격자가 되지만, 다중발파의 조파영역은 장약량과 발파공의 수에 따라 결정된다.
본 연구에서는 수중폭파에 의한 수면파형에 고립파 근사이론을 적용하며, Lee et al.(2016)이 다양한 고립파형을 조파할 수 있는 제안한 방법을 이용한다. 고립파의 수면파형은 Dean and Dalrymple(1991)의 근사이론을 이용하며, 시간파형과 수립자의 수평유속은 식 (12)-(13)과 같다.
여기서 ηmax는 최대수면높이, C는 식 (14)과 같은 파속, λ는 수면변위와 최대수면변위와의 비(η/ηmax), ∈는 최대수면변위와 수심과의 비(ηmax/h), zh는 바닥과 수립자의 연직거리와 수심과의 비이다.
2.3 수중발파에 의한 수면파를 위한 경계조건
대부분의 수치파동수조는 진행파의 양방향에 부가감쇠영역을 설치하고, 측면경계에 있어서 Non-slip 또는 Slip 조건을 사용한다. 이처럼 적용할 경우, 수중발파에 의한 수면파는 4방향으로 전파되기 때문에 측면경계에서 반사파가 발생하여 파동장 교란이 발생하게 된다. 이것을 보완하기 위해 Hur and Lee(2011)는 수치파동수조에서 경사입사파의 조파를 위한 수조경계의 반사파 제어를 Fig. 3이 같은 부가감쇠영역(Added dissipation zone)과 방사형 파랑감쇠계수(β; Wave damping coefficient)를 설정하였다. 여기서 β는 다음 식 (15)에 대입되어 연직유속(w)만을 서서히 감소시킨다.
개경계 조건은 수치파동수조에서 생성된 에너지를 수조 밖으로 완벽하게 배출하기 위한 것으로 식 (16)처럼 Hinatsu(1992)의 개경계 처리법을 이용한다. 식 (16)에서 ϕ는 유속과 같은 물리량을 말한다.
3. 수치모델의 검증
3.1 검증을 위한 수치파동수조의 구성 및 조건
LES-WASS-3D ver. 2.0을 적용한 연구들에서는 파랑의 진행방향 양쪽에 무반사 조파시스템을 적용하였다(Lee et al., 2017; Lee et al., 2018). 그러나 수중발파에 의한 수면파는 사방으로 전파된다. 따라서 수중발파에 의한 수면파 전파모의에 앞서 이용하는 수치파동수조의 검증이 요구된다.
Fig. 4와 같이 구성된 수치파동수조의 정중앙에서 발파에 의한 수면파를 생성하여 그 전파과정을 경험적 값과 비교⋅분석한다. 1km×1km×15m 해석영역을 설정하여 수평 격자(∆x, ∆y)는 5m, 수직 격자(∆z)는 0.5m의 수치파동수조를 구성하며, 그 외곽에는 Fig. 3과 같이 부가감쇠영역 및 개경계조건을 고려한다.
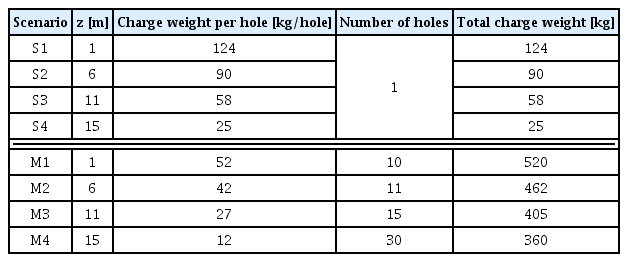
이용하는 계산조건은 Table 1과 같으며, 토도 제거를 위한 수중발파 시나리오를 그대로 적용하여 수치파동수조를 검증한다. 수중발파 시나리오의 단계는 수심 -1m, -6m, -11m, -15m 순으로 진행한다. 그리고 단일발파(Scenario S1-S4)와 다중발파(Scenario M1-M4)로 구분하여 수중발파에 따른 수면파의 생성 및 전파를 모의한다. 다중발파에서 발파공의 간격은 5m이다. 그리고 모든 수치모의의 초기계산간격(∆t)을 1/100초로 설정하고, CFL(Courant-Friedrichs-Lewy)조건을 만족하게 조절한다.
3.2 수면파의 비교⋅검증
Fig. 5는 단일발파, Fig. 6은 다중발파에 의해 발생한 수면파가 초기 수면형의 반경(R)에서 500m까지 전파하는 과정에서의 최대수위를 비교한 것이다. 여기서 검정 실선은 식 (4)에 의한 값, 붉은 동그라미는 수면파의 최대수위를 각각 나타낸다.

Comparisons between theoretical(red circle) and numerical(black line) results showing the maximum elevation of water wave by a single-charge blasting

Comparisons between theoretical value and numerical result showing the maximum elevation of water wave by a multiple-charge blasting
Fig. 5와 Fig. 6에서 각각의 R지점에서 경험식 (4)에 의한 값과 수치모의결과 매우 잘 일치함을 알 수 있다. 이것은 발파지점(조파원천)에서 발생하는 수면파의 생성과정이 타당하기 때문이다. 또한 R지점에서 500m 지점까지 수면파가 전파되는 과정에서 최대수위가 높은 정확도로 일치한다. 이것은 본 연구에서 수치파동수조가 발파에 의한 수면파 전파모의에 적합함을 보여준다.
이로써 본 연구에서 제안한 수중폭파에 의한 수면파의 생성 방법, 수치파동수조에서의 수면파 전파모의에 대한 타당성 및 유효성이 입증되었다.
4. 수치모의
4.1 수치파동수조의 구성 및 조건
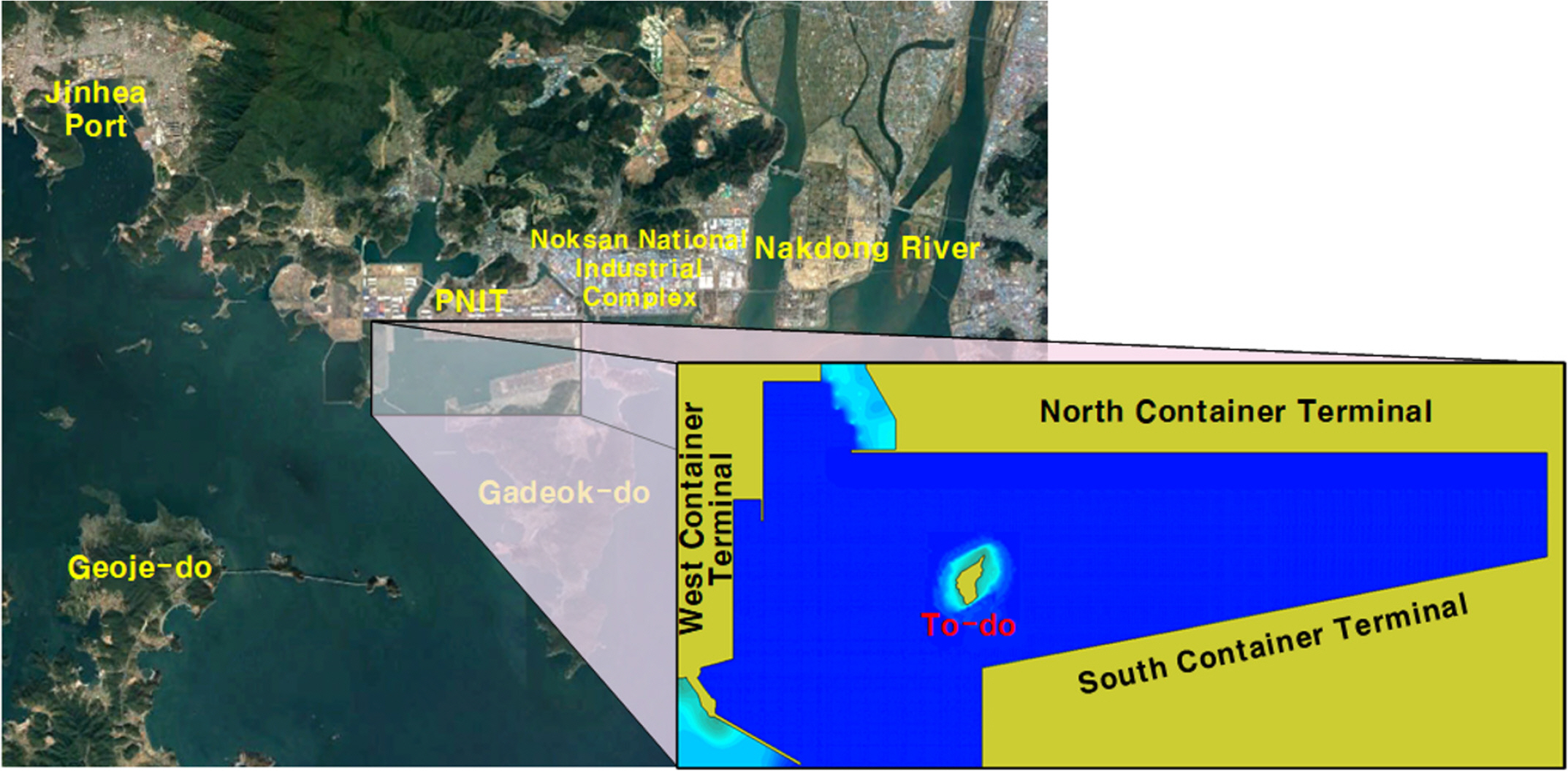
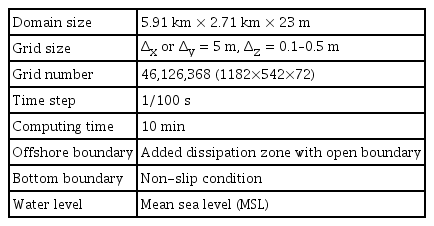
본 연구에서는 토도 제거를 위한 수중발파 시나리오별 수면파의 생성 및 전파를 모의하기 위하여 Fig. 7에 나타낸 부산신항만의 전 해역을 수치파동수조의 계산영역으로 설정한다. Table 2에 나타낸 것과 같이 5.91km×2.71km×23m의 계산영역을 수평 방향으로 5m 등간격 분할하고, 수직 방향으로 0.1-0.5m 부등간격 분할한다. 이 과정에서 부산신항만 내의 경사지형은 Hur et al.(2008)의 경사면 처리기법을 적용한다. 나머지 상세한 수치모의조건은 Table 2과 같다.
단계별 수중발파 시나리오는 Table 1과 같으며, 육상제거가 완료된 수심 -1m를 시작하여 수심 -6m, 수심 -11m 그리고 마지막으로 수심 -15m까지 Table 3과 같이 총 4단계로 나누어 수치모의를 수행한다. 수중발파 시나리오별 장약량은 Table 1에서 기술한 바와 같다. 발파지점에 따른 수면파의 영향 검토는 수치파동수조 검증에서 가장 큰 수면변동이 발생한 다중발파의 시나리오 4단계 조건(Scenario M4; 수심 -15m)에서 동서남북 가장자리를 발파지점으로 한다(Table 4 참조). 그리고 부산신항만 컨테이너 터미널에서 미치는 영향을 정량적으로 검토하기 위하여 동서남북 직선거리가 가장 가까운 터미널의 4지점에서 시간파형을 측정한다(Table 5 참조).
4.2 수면파의 전파
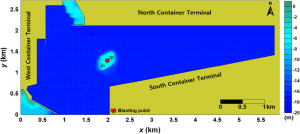
Fig. 8과 Fig. 9는 다중발파에 의해 생성된 수면파가 전파하는 과정을 30초 간격으로 나타낸 공간파형이다. Fig. 8은 Scenario M1으로서 발파수심 1m에 총 장약량이 520kg, Fig. 9는 Scenario M4로서 발파수심 -15m, 총장약량이 360kg의 경우를 각각 나타낸다.

Temporal and spatial distributions of water surface elevations by underwater blasting in case of Scenario M1

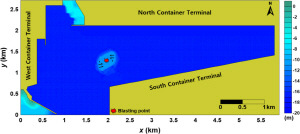
Temporal and spatial distributions of water surface elevations by underwater blasting in case of Scenario M4
Fig. 8에서는 장약량이 가장 많음에도 불구하고, 발파수심이 -1m로 낮으므로 폭파에너지가 얇은 수층으로 전달됨으로 발생하는 수면파의 진폭이 작다. 그 뿐 아니라 수심 -1m의 토도 지형이 남북으로 긴 타원형인 관계로 방사형으로 전파되던 수면파가 남북방향의 양쪽에서 굴절되어 수면파의 중첩이 발생한다. 반면에 Fig. 9에서는 발파수심이 -15m로 가장 깊으므로 장약량이 적음에도 폭파에너지가 전 수층으로 전달됨으로 수면파의 진폭이 크다. 또한 수면파의 전파에 있어서 토도의 지반높이(-15m)와 항로의 수심(-17m)과 차이가 작은 관계로 방사형으로 그대로 퍼져나간다. 이 과정에서 수면파는 가까운 남쪽과 북쪽의 컨테이너 터미널 그리고 서쪽 컨테이너 터미널 순으로 도달한다. 그리고 컨테이너 터미널 안벽에 의한 반사파 간의 중첩이 연속적으로 발생함을 알 수 있다.
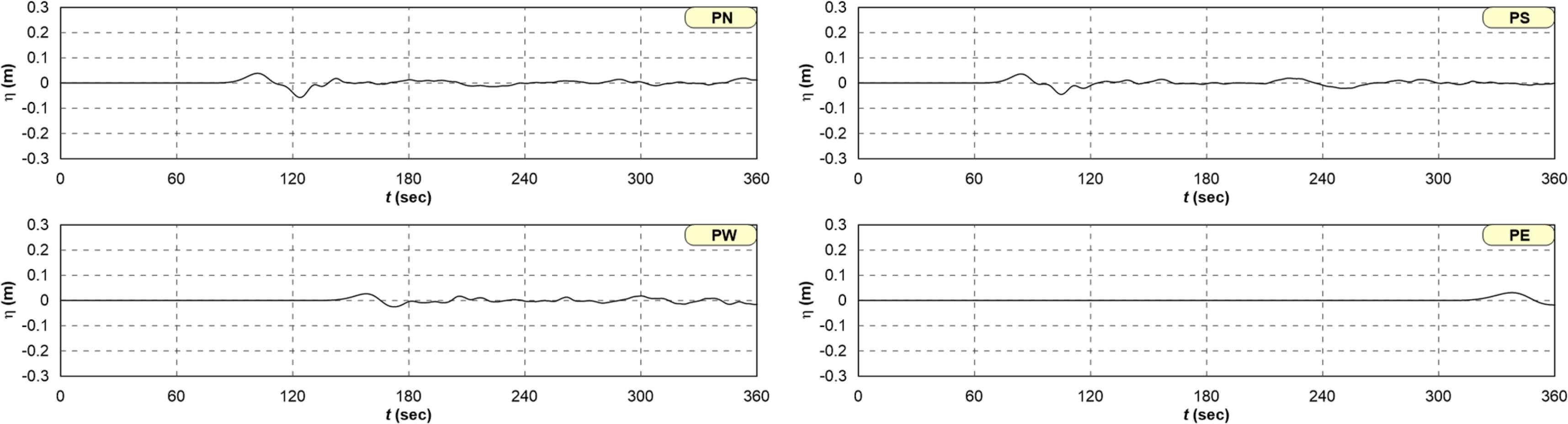
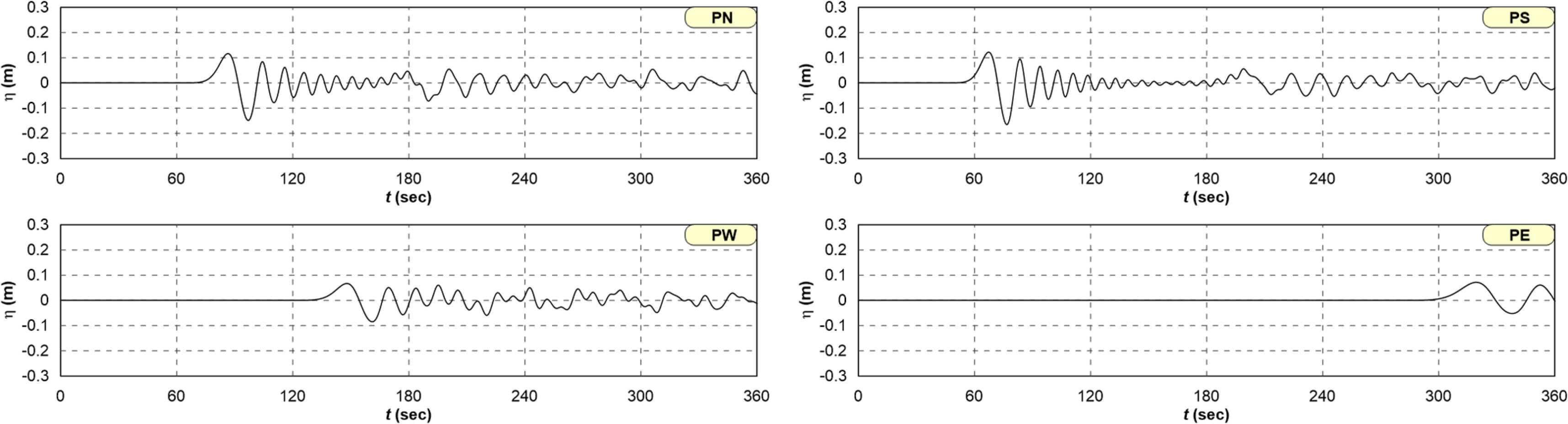
Fig. 10과 Fig. 11은 Table 5에 나타낸 PN, PS, PW, PE에서의 시간파형이며, 수중발파지점에서 직선거리가 가장 가까운 다목적 터미널, 남, 서, 북 컨테이너 터미널의 한 지점이다. 여기서 Fig. 10은 Scenario M1, Fig. 11은 Scenario M4의 경우이다.
Fig. 10과 Fig. 11로부터 수중발파지점으로부터 직선거리가 가까운 PS, PN, PW, PE 순으로 수면변위가 나타난다. Fig. 10은 전술한 Fig. 8에서 논의한 것과 같이 전체적으로 수면변위가 크지 않다. Fig. 11은 상대적으로 수면변위가 크고, PS, PN, PW, PE 순으로 수면파의 파고가 큰 것을 알 수 있다.
Table 6은 수중발파 시나리오별 PS, PN, PW, PE에서의 최대수위(ηmax)가 발생하는 시간을 각각 나타낸 것이다. 전술처럼 수중발파지점으로부터 직선거리가 가까운 PS, PN, PW, PE 순으로 수면파가 도달한다. 그리고 단일발파 및 다중발파에서 발파수심이 깊어 수면파동이 큰 시나리오(Scenario S4와 M4)에서 각각의 안벽에 도달하는 시간이 빨라진다. 이것은 Dean and Dalrymple(1991)의 고립파 근사이론과 같이 수심과 수면변위가 클수록 파속(식 (14))이 빠르기 때문이다.
4.3 최대수위분포
Fig. 12는 단일 수중발파에서 시나리오별 최대수위(ηmax)의 공간분포를 나타낸다. Fig. 12에서 (a), (b), (c), (d)는 Scenario S1-S4를 나타내며, 발파수심은 -1m, -6m, -11m, -15m, 장약량은 124kg, 90kg, 58kg, 25kg이다.
Fig. 12로부터 장약량이 많음에도 불구하고, Scenario S1에서 가장 작은 ηmax가 발생하는 것은 발파수심이 낮아 수중발파에 의한 수면파동이 발달하지 못하기 때문이며, Fig. 8을 통해 확인할 수 있었다. 따라서 발파수심이 깊을수록 수중발파에 의한 ηmax가 증가하고, 영향 범위도 증가함을 알 수 있다.
Fig. 13은 다중 수중발파에서 시나리오별 ηmax의 공간분포이며, (a), (b), (c), (d)는 Scenario M1-M4를 나타내며, 발파수심은 -1m, -6m, -11m, -15m, 장약량은 520kg, 462kg, 405kg, 360kg이다.
Fig. 13을 Fig. 12와 비교하면, 같은 발파수심에서 장약량이 많은 다중발파의 경우(즉, Fig. 12보다 Fig. 13)에 ηmax가 클 뿐 아니라, 수면파의 영향 범위도 넓어진다. 한편 발파수심이 15m인 Scenario S4와 M4를 직접 비교하면, Scenario M4가 장약량이 14.4배 많음에도 ηmax 와 영향 범위가 많이 증가하지 않는다. 이것은 Le Méhauté and Wang(1996)의 제안식 (4)에서도 알 수 있듯이 장약량(W)에 따른 ηmax의 변화가 크지 않기 때문이다.
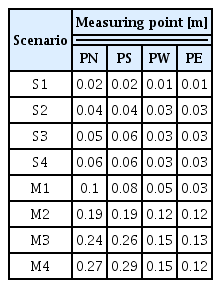
부산신항만 컨테이너 터미널에 미치는 영향을 정량적으로 분석하기 위하여 Table 5에 나타낸 각각의 터미널의 측정지점 PN, PS, PW, PE에서의 ηmax를 Table 7에 나타낸다.
Table 7로부터 알 수 있듯이 단일 수중발파 Scenario S1-S4는 부산신항만 컨테이너 터미널에 미치는 영향이 미미하다. 그리고 다중발파에서 가장 큰 수면파동이 발생하는 Scenario M4의 경우에 직선거리가 가장 짧은 남컨테이너 터미널 PS지점의 ηmax는 0.29m로 그렇게 크지 않다.
본 연구에서 검토한 단일발파 및 다중발파 그리고 단계별 시나리오에 따른 수면파는 주변 컨테이너 터미널에 미치는 영향이 그다지 크지 않다. 하지만 수중발파지점이 터미널에 가까울수록 ηmax가 증가하는 경향이 나타남으로 Table 4의 발파지점에 따른 수면파의 특성을 다음에서 검토한다.
4.4 발파지점별 수면파의 전파
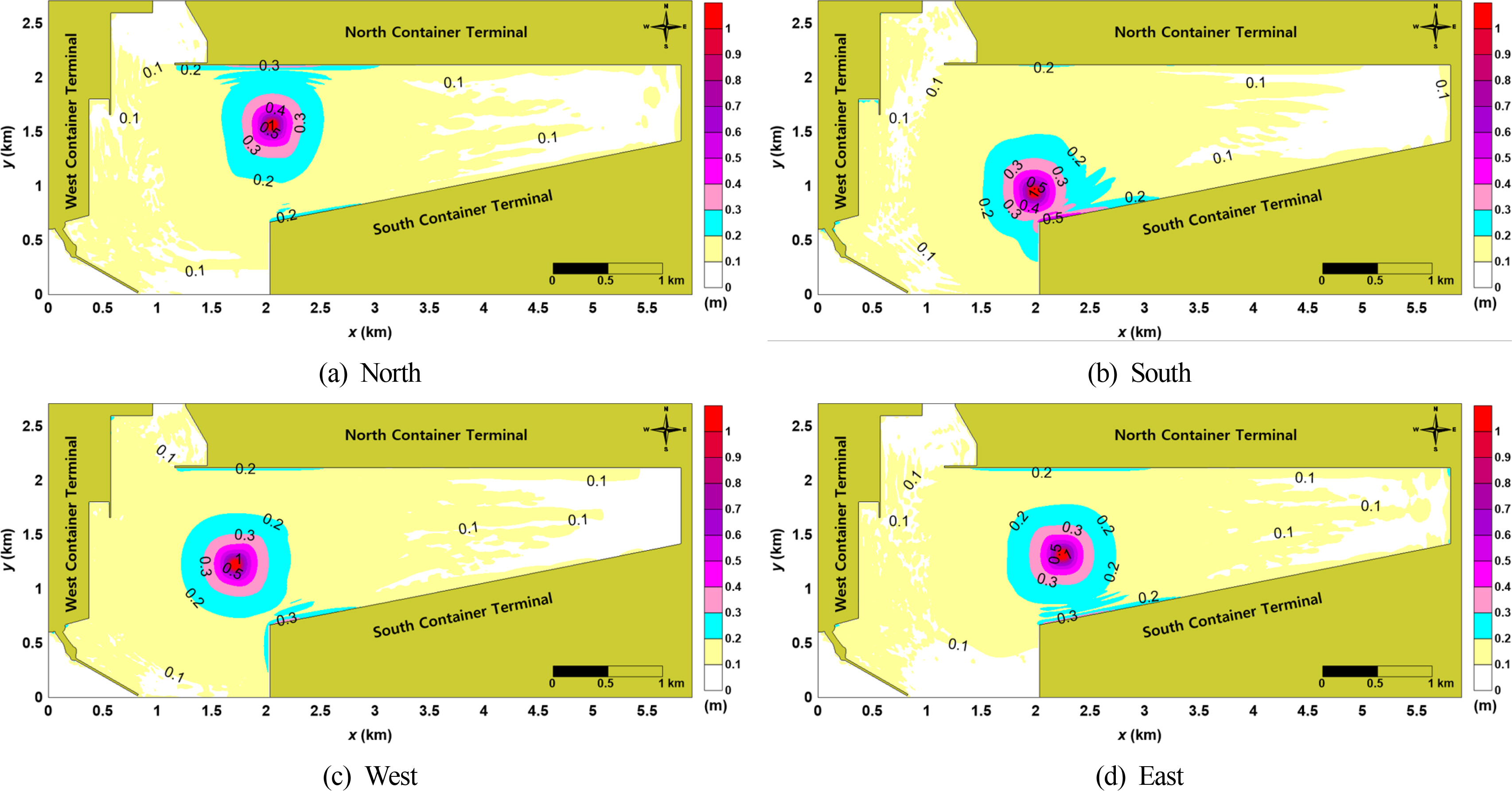
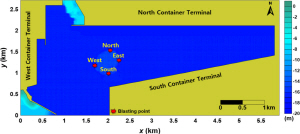
Fig. 14는 Table 7에서 가장 큰 ηmax가 발생한 Scenario M4에서 Table 4에 표시한 발파지점별 ηmax의 공간분포를 나타낸다. Fig. 14에서 (a)는 북쪽, (b)는 남쪽, (c)는 서쪽, (d)는 동쪽 각각의 가장자리에서 수중발파를 진행한 결과이다.
Fig. 14로부터 동쪽의 다목적 터미널을 제외하고는 수중발파 지점에 인접할수록 남쪽, 북쪽, 서쪽 컨테이너 터미널에서 전반적으로 ηmax가 상승하고, 영향 범위가 넓어지는 경향을 보인다. 이것은 수중발파에 의한 수면파가 방사형으로 전파되기 때문에 영향권을 벗어나는 경우엔 ηmax가 매우 작지만, 그렇지 않으면 컨테이너 터미널 안벽에서 유의미한 ηmax가 발생함을 알 수 있다. 이에 정량적 분석을 위해 Table 8에 각 컨테이너 터미널의 측정지점 PN, PS, PW, PE에서의 ηmax를 나타낸다.
Table 8로부터 각 컨테이너 터미널로부터 수중발파지점이 가까운 경우, ηmax가 증가한다. 특히, 토도로부터 직선거리가 가까운 남과 북의 컨테이너 터미널에서 ηmax가 증가하며, 남쪽 발파 시에 PS에서 0.2m, 북쪽 발파 시에 PN에서 0.09m 크다. 그리고 토도와 거리가 상대적으로 먼 서쪽 컨테이너 터미널과 다목적 터미널의 측정지점 PW와 PN에서는 ηmax 의 증가가 크지 않다.
5. 결론 및 고찰
본 연구에서는 수중발파에 의한 수면파의 발생 및 전파를 모의하기 위하여 3차원 수치파동수조(LES-WASS-3D Ver. 2.0; Lee and Hur, 2014a)를 개량하였다. 그 과정에서 수중발파에 의한 수면파를 생성을 위하여 발파수심과 장약량에 따라 파 제원을 추정할 수 있는 경험식을 수면파 조파에 이용하였다. 그리고 수치파동수조에서 수중발파에 따른 수면파의 생성과 전파 과정에서의 최대수위분포를 비교⋅검증하였다. 이 수치파동수조에 토도 제거를 위한 수중발파 시나리오를 적용하여 수면파 생성과 전파를 모의하였다. 이를 통해 얻어진 주요한 결과를 다음과 같이 기술한다.
(1) 본 연구에서는 수중발파에 의한 수면파를 생성하기 위하여 Le Méhauté and Wang(1996)의 경험식을 무반사 조파시스템에 적용하는 조파방법을 제안하였다. 그리고 비교⋅검증을 통해 수중발파에 따른 수면파의 생성 및 전파에 관한 수치파동수조의 타당성 및 유효성을 확보하였다.
(2) 3차원 수치파동수조에서 토도 제거를 위한 수중발파 시나리오별 수면파의 생성 및 전파를 모의하였다. 그 결과 단일/다중발파의 각 조건에서 장약량이 많을수록, 발파수심이 깊을수록 수면파동이 커졌다. 또한 발파수심이 깊을수록 ηmax가 크고, 파속이 증가하여 컨테이너 터미널 안벽에 도달하는 시간이 빨라졌다.
(3) 수중발파지점이 각 컨테이너 터미널에 가까울수록 ηmax가 커지는 경향을 나타내었다. 특히, 남과 북의 컨테이너 터미널 안벽에서 중앙발파보다 남쪽 또는 북쪽발파 시에 ηmax가 증가하였다. 그리고 서컨테이너 및 다목적 터미널에서는 증가 폭이 크지 않았다.
(4) 본 연구에서 검토한 토도 제거를 위한 수중발파 시나리오에 따른 수면파는 가동 중인 부산신항만의 터미널에 미치는 영향이 크지 않음을 확인하였다.
수중폭발에 의한 충격파, 압력강하에 의한 공동현상, 기포의 생성과 상승(팽창과 수축) 등의 복합적 상호작용 때문에 발생하는 수면파동을 CFD를 이용하여 직접 모의할 수 있지만, 광역에서의 전파과정까지 추정하는 것은 사실상 불가능하다. 따라서 수중발파에 의한 수면파가 주변 해역에 미치는 영향을 분석에는 본 연구처럼 장약량과 발파수심에 따른 수면파의 제원을 산정하여 수면파를 생성하는 것이 더 효과적이다. 향후, 부산신항만에서 토도 제거를 위해 진행하고 있는 수중발파 시의 수면변위 자료를 수집하여 수치파동수조에서 실제 조건을 적용한 모의결과와 비교⋅검토를 수행할 예정이다.
Acknowledgements
이 성과는 2018년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. NRF-2018R1C1B6007461).