Article information

J. Ocean Eng. Technol. 2019;33(5):411-420

Publication date (electronic) : 2019 October 31

doi : https://doi.org/10.26748/KSOE.2019.046

Woongshik Nam^,*

^*Department of marine technology, Norwegian University of Science and Technology, Trondheim, Norway

남웅식^,*

^*노르웨이 과학기술대학교 해양공학과

Corresponding author Woongshik Nam: +47-7359-5697 hnws871105@naver.com

It is noted that this paper is revised edition based on proceedings of Conference of KAOSTS 2019 in Jeju.

Received 2019 May 28; Revised 2019 September 3; Accepted 2019 October 16.

Trans Abstract

1. 서 론

지난 수십 년 동안 지구 온난화는 북극항로(Northern sea route, NSR)에서의 선박 운송 및 석유, 가스와 같은 에너지 자원의 추출 등 북극 활동의 상당한 증가를 야기했다. 북극 지역을 덮고 있는 빙(Ice)의 감소로 수에즈 운하 대신 북극항로를 이용하면서 상당한 경제적 이점을 얻을 수 있다. 하지만 북극항로를 이용하는 선박 및 해양 구조물은 극한 환경 조건, 특히 영하의 기온과 빙 충돌의 위험에 노출된다. 일반적으로 북극해의 평균 온도는 여름철 10℃, 겨울철 -40℃, 기록된 가장 낮은 온도는 -68℃로 알려져 있다(Park et al., 2015a). 이러한 극한 환경에 대비하여 구조물의 내충돌 성능은 설계 단계에서부터 검증되어야 하지만 저온에서의 재료 거동 모델링과 구조 설계에 대한 적절한 지침이 부족하다.

선체 구조 설계 단계에서 빙 하중 저항력을 예측하는 방법으로 International Association of Classification Societies(IACS, 2011)와 같은 Ice class rules 기반 간편식의 사용이 있다. 규칙 기반의 간편식은 간소한 방법론을 제공하지만, 모든 충돌 상황에서 발생하는 빙 하중을 예측하기에는 제한적이므로 그 대안으로써 수치 해석을 이용한 빙하-구조물 충돌 상호작용의 연구가 수행되어 왔다.

그 중 Hakala(1980)는 유한 요소법을 이용해 내빙 구조물의 과하중 조건에서의 구조물 거동을 연구하였다. Jebaraj et al. (1992)은 빙하-구조물 상호 작용을 모사하기 위해 유한 요소법을 사용하였으며 이 연구에서는 선박과 빙하 사이의 충돌 속도 및 각도, 얼음 두께의 변화에 따라 빙하의 파단을 야기하는 충격 하중의 크기를 조사하였다.

수치 해석을 이용한 빙하-구조물의 상호작용을 연구하기 위해서 신뢰할 수 있는 빙 재료 모델(Ice material model)의 사용이 필수적이다. Liu et al.(2011)는 빙 재료 거동을 모사하기 위해 Tsai-Wu 항복 함수 기반의 탄성-완전 소성 재료 모델을 제시하였으며, 선측 및 선수부의 빙 충돌 해석을 통해 이 재료 모델의 유효성을 증명하였다. 이 외에도, Jia et al.(2009), Gagnon(2011), Gao et al.(2015) 등에서 빙 재료 모델의 연구가 이루어져 왔지만, 현재까지 빙 재료의 거동을 완벽히 정의하는 재료 모델은 없는 실정이다. 빙 재료의 특성치는 주변 환경 조건에 큰 영향을 받게 되는데, 이는 빙의 형성 과정과 성장 속도에 차이가 발생하기 때문이다. 일반적으로 Solid ice, Brine cells, 가스, 기공 등으로 구성되는 해빙(Sea ice)은 성장하면서 이 요소들의 비율과 배열에 따라 빙 재료의 특성치가 변한다. 그러므로 빙의 특성치는 분포한 지역, 나이에 따라 분류되어 정의되어야 한다. 예를 들어 1년생 빙의 결정체는 해수 수평 방향 보다 수직 방향의 성장 속도가 더 빠르기 때문에 1년생 빙은 직교 이방성의 특성을 갖는 반면 다년생 빙은 등방성 재료로써 간주된다. 극지방에 분포된 빙하의 경우 다년생 빙의 범주에 해당하기 때문에, 이 경우 빙 재료 모델은 등방성 재료로써 정의되어야 한다.

최근의 구조물-빙 충격 상호작용의 수치적 연구(Matsui et al., 2018; Yu et al., 2018; Zhu et al., 2018)를 살펴보면, 피 충돌 구조물을 구성하는 강재의 특성치는 환경 온도에 독립적인 것으로 가정되었다. 이 연구들에서는 상온(20℃)의 준정적 단축 인장 실험에서 얻은 강재 특성치와 파단 기준을 수치 해석에 적용하였지만, 북극항로와 같은 저온 환경에서의 강재 특성치는 고려하지 않았다. 많은 연구와 실험 데이터에서 증명되었듯이 강재의 기계적 특성치는 환경 온도에 종속적이며, 온도에 따라 전혀 다른 재료 거동을 갖는다. 그러므로 북극 환경에 노출된 구조물-빙하 충격 상호작용의 수치 해석을 수행하기 위해서는 온도에 따른 재료의 기계적 특성치를 정의해 줄 필요가 있다.

본 연구에서는 구조물-빙 충격 하중의 상호작용을 연구하기 위해 유한 요소법을 이용한 수치 해석을 수행한다. 수치 해석에는 가상의 보강판을 모델링하고, 빙하 충격 하중을 부여하여 사고 한계 상태(ALS, Accidental limit state)의 관점으로 보강판의 구조적 거동을 분석한다. Finnish-Swedish Ice Class Rules(FSICR, 2008)의 규정에 따라 IA super class 등급의 격자 구조물을 가정하여, Hull plate, Web frame, Stringer, Flat bar로 가상의 보강판을 구성한다. 빙 재료 거동을 모사하기 위해 Liu et al.(2011)가 제시한 탄성-완전 소성 재료 모델과 파단 기준을 적용하며, 보강판을 구성하는 강재의 거동은 등방 경화, 소성 유동 법칙 기반의 von-Mises 항복 기준으로 정의된다. 보수적으로 가정된 북극항로의 환경 온도(-50℃)와 상온에 노출된 보강판이 동일한 빙 충격 하중으로부터 갖는 구조적 거동을 비교, 분석한다.

2. 빙 재료 모델

2.1 Liu et al.(2011)의 빙 재료 모델

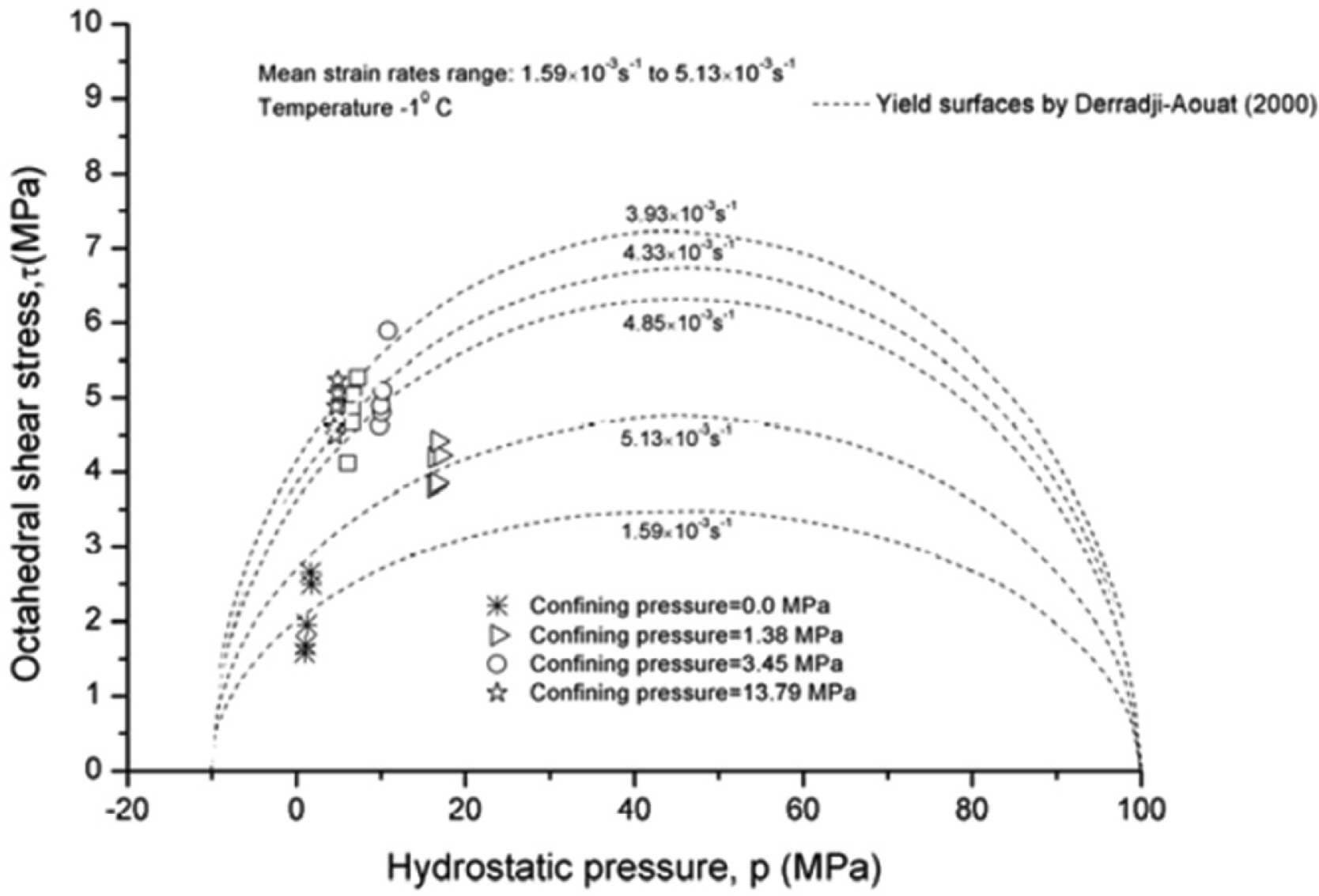
빙 재료의 항복 함수 확립을 위해 Sammonds et al.(1989), Gagnon and Gammon(1995), Melanson et al.(1999)는 가압 유체를 빙 시편에 적용하고 추가적인 축 하중을 부여한 삼축 하중 실험을 수행하였다. 많은 연구자들은 이러한 실험 결과로부터 얻은 응력-변형률 또는 응력-압력 관계를 기반으로 빙 재료의 항복 함수를 확립하였다. 그 중 Gagnon and Gammon(1995)의 실험 데이터를 이용해 Derradji-Aouat(2000)은 식 (1)과 같은 타원형 항복 곡면을 갖는 빙 재료 모델의 항복 함수를 제시하였다. Liu et al.(2011)은 Gagnon and Gammon(1995)의 실험 데이터와 Derradji-Aouat(2000)의 타원형 항복 곡면을 Fig. 1과 같이 정리하였다.

Fig. 1.

Test data and elliptical yield surfaces for ice, referred from Liu (2011)

(1) (τ−ητmax)2+(p−λpc)

여기서 τ_max, p_c, λ, η는 실험 데이터로부터 교정되는 상수이며, τ와 p는 각각 8면체 응력과 정수압 응력을 나타낸다. Derradji-Aouat(2000)가 제시한 타원형 항복 곡면은 실험 데이터와 같이 Fig. 1에 도시하였다.

Derradji-Aouat(2000)가 제시한 항복 모델에서 η = 0인 경우, Tsai-Wu 항복 함수와 같게 되며 Liu et al.(2011)는 바로 이 Tsai-Wu 항복 함수를 적용해 빙하-구조물 충돌의 유한요소 해석을 수행하였다. 등방성 빙 재료의 Tsai-Wu 항복 함수는 식 (2)와 같다.

(2) f(p,q)=q−a0+a1p+a2p2

여기서 q는 von-Mises 응력이며, a₀, a₁, a₂는 실험 결과로부터 얻어지는 상수이다. Liu et al.(2011)는 수치적 편의성을 위해 식 (2)를 식 (3)과 같은 p-J₂의 함수로써 나타내었다.

(3) f(p,J2)=J2−(a0+a1p+a2p2)

여기서 J₂는 2차 편차 응력 불변량이다. 본 연구에서 수치해석에 사용하는 빙 재료 항복 함수에는 Kierkegaard(1993)에서 제시한 상수 a₀=2.588, a₁=8.63, a₂=-0.163을 적용하였다. Liu et al. (2011)은 빙 재료의 파단을 모사하기 위해 등가 소성 변형률을 기반으로 하는 정수압 응력 함수의 경험적 파단 기준식을 제시하였으며 이는 식 (4)와 같다.

(4) εf=ε0(pp2−0.5)2

여기서 ε₀는 초기 파단 변형률로써 실험 데이터로부터 교정되는 상수이며, p₂는 항복 함수 식 (3)의 서로 다른 두 근 중 큰 값을 갖는 근이다. 본 연구에서 적용한 파단 기준식을 최종 파단 변형률 ε_f^- 정수압 응력 p의 관계로 Fig. 2에 도시하였다. 응력이 탄성 영역을 지나 소성영역에서 항복 곡면의 궤도를 따라 움직이는 동안 등가 소성 변형률 εeqp이 최종 파단 변형률보다 크거나(εeqp≥εf), 정수압 응력 p가 Cut-off pressure, p_cut보다 작은 경우 요소 내의 모든 응력은 0으로 수렴, 강성을 잃게 되면서 요소는 삭제된다. 초기 파단 변형률 ε₀의 교정 과정은 본 논문의 2.2장에 서술하였으며 –2MPa의 p_cut를 적용하였다.

Fig. 2.

Failure strain curve as a function of pressure, where ε₀=0.12

빙하에 하중이 부여되면 빙 재료는 탄성 단계, 더 나아가 소성 단계의 변형을 경험하게 된다. 탄성 영역 안에서 빙 재료의 응력은 일반적인 Hook’s law를 통해 계산이 된다. 만약 응력의 상태가 타원형의 항복 곡면에 도달하게 된다면 이후의 재료는 완전 소성 상태가 된다. 이러한 완전 소성 영역에서 응력은 Return-mapping algorithm을 이용한 반복 계산을 통해 계산된다. 소성 이론식의 적분을 위해 변형률 독립 재료 모델의 경우 정확하고 효율적인 계산 결과를 보여주는 Cutting-plane algorithm(Ortiz and Simo, 1986)을 적용하였다. 본 연구에서는 상용 유한 요소 해석 프로그램 ABAQUS/Explicit의 사용자 서브루틴 VUMAT사용하여 Liu et al.(2011)의 빙 재료 모델을 수치 해석에 이식하였다.

2.2 빙 재료 모델 검증

여기서는 ABAQUS/Explicit VUMAT을 통해 이식한 빙 재료 모델의 유효성 검증을 수행한다. 검증은 다음과 같이 두 단계로 구성된다.

(1) 하나의 가상 빙 요소를 모델링 한 후, 임의의 하중과 경계조건을 부여해 요소의 p-J₂ 관계를 조사한다. 빙 재료 모델링에는 C3D8R(감차적분 8절점 사각기둥 요소)를 사용하였으며 가로, 세로, 높이 각각 100mm의 길이를 갖는다(Fig. 3). 빙 재료의 밀도 900kg/m³, Poisson’s ratio 0.3, 탄성계수 9.5GPa을 설정하였다. 변위 제어를 통해 부여한 하중 및 빙 요소의 경계 조건은 Table 1에 서술하였다. 수치 해석 결과를 이식한 재료 모델의 항복 함수 이론식과 비교하여 Fig. 4에 나타내었다. Fig. 4에서 볼 수 있듯이 각 Case마다 탄성 영역에서 소성 영역으로의 전이속도는 다르지만, 타원 형의 항복 함수 이론식을 잘 따르고 있는 것을 확인할 수 있다.

Fig. 3.

Fictitious ice element presenting node numbers

Table 1.

Boundary conditions applied to the ice element

Fig. 4.

Theoretical yield surface (Equation 3) and the material behavior of ice for each case

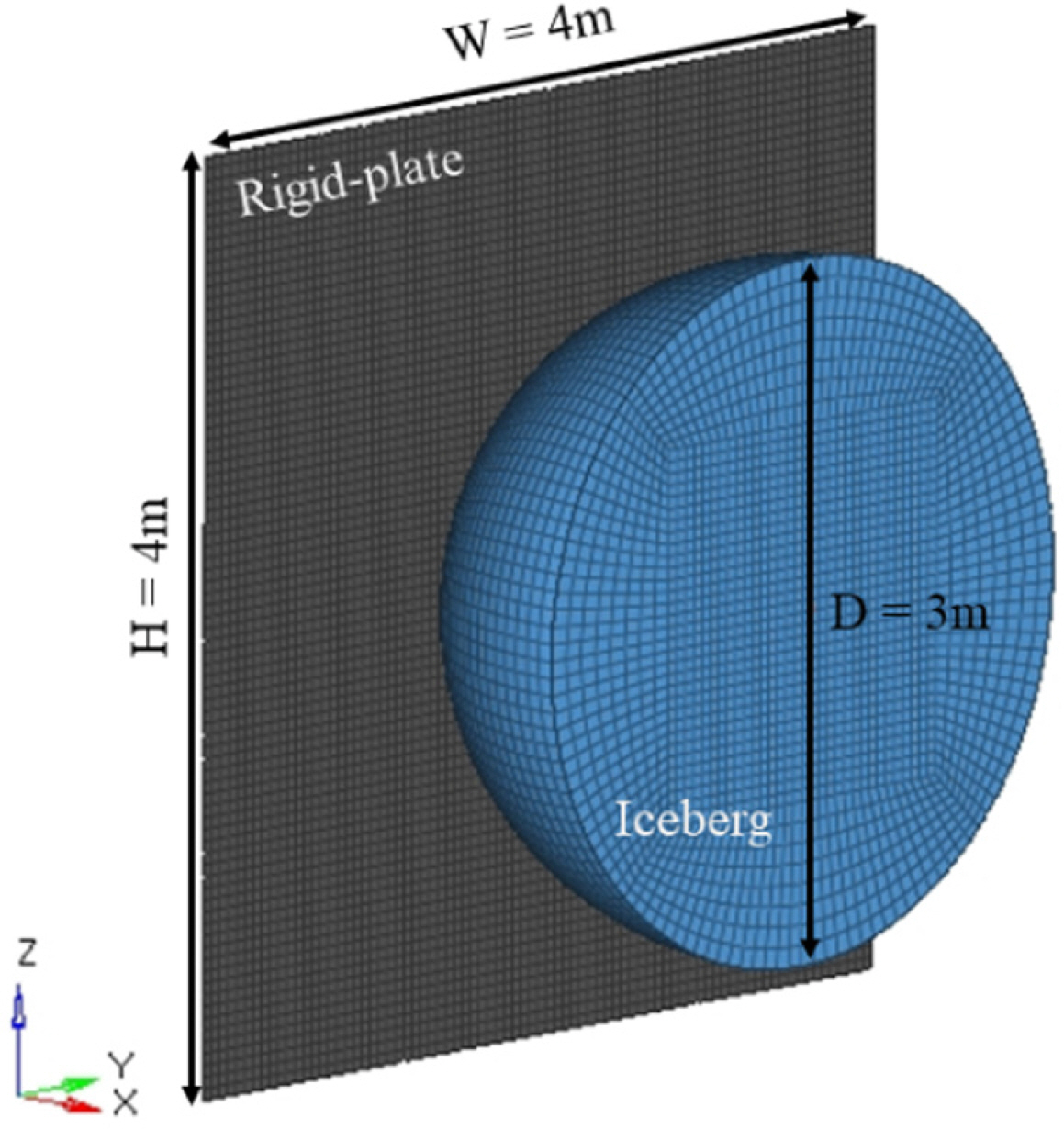
(2) 두 번째 검증 단계로써, 강체판(Rigid-plate)와 빙하의 충돌수치 해석을 수행한다. 수치 해석 결과로써 충돌 거리(Crushing distance)에 따른 반력 곡선을 도출해 ISO(International Organization of Standardization) 권고 및 기존 연구에서 제시한 결과와 비교한다. 이 과정에서는 빙 재료 모델의 검증과 이식한 파단 기준식에 필요한 상수 ε₀ 교정을 동시에 수행한다. 여기서 빙하는 DNV(2006) 권고 중 하나인 구(Sphere) 형상으로 1.5m의 반경을 가지며, 강체판은 4m의 높이와 너비를 갖는 정사각 형태로 모델링 되었다(Fig. 5).

Fig. 5.

Finite element model of rigid-plate and iceberg

빙하는 2m/s의 속도로 X축 단축 방향으로 이동하며 나머지 두축(Y, Z)의 변위와 모든 축의 회전 변위는 고정된다. 강체판에는 고정 경계조건을 부여해 충돌 동안 어느 방향으로도 변위를 갖지 않도록 하였다. 충돌 해석에는 ABAQUS/Explicit에서 제공하는 Surface-Node contact algorithm을 적용하였으며 기존 연구(Liu et al., 2011; Gao et al., 2015)를 참고하여 강체판과 빙하 사이에는 0.15의 마찰 계수를 적용하였다. 빙하와 강체판의 모델링에는 각각 C3D8R, R3D4(3차원 4절점 강체 요소) 요소를 사용하였다. 수치 해석에서 발생하는 Hourglass control energy의 크기를 줄이기 위해 변위 자유도 기반 Hourglass control algorithm을 적용하였으며, 그 결과 전체 충돌 해석 동안 Hourglass control energy는 빙하의 Internal energy의 3% 이하의 비율을 갖는다.

여기서 수행하는 수치 해석 결과에 영향을 주는 요인으로 마찰 계수, 빙 재료의 물성치, 파단 기준(초기 파단 변형률 ε₀)와 요소 크기 등이 있다. 본 논문에서는 Kim(2014)를 참고하여 다음과 같은 단계별 절차로 요소 크기 민감도를 줄이고자 하였다.

- 주어진 충돌 해석에서 충돌-피충돌 구조물 사이의 적절한 마찰 계수를 설정

- 빙 재료 모델의 상수 결정 : 빙 유형 및 빙 재료의 실험 결과를 참고해 a₀, a₁, a₂를 선택

- 요소 길이에 따라 요구되는 계산 시간을 고려하여 빙 요소의 길이를 결정(본 연구에서는 80mm)

- 마찰 계수, 모든 빙 재료 모델의 상수 및 요소 크기 결정 후 수치 해석을 수행 : 수치 해석과 실험(또는 실측 데이터) 결과를 비교하고 실험 결과와 유사한 결과를 도출할 수 있도록 파단 기준의 초기 파단 변형률 ε₀을 교정

본 연구에서는 기존 연구(Liu et al., 2011; Kim, 2014; Gao et al., 2015)의 참고 및 계산 시간을 고려해 빙 요소 80mm, 강체판 요소 100mm의 크기로 구조물을 모델링 하였다. 강체판의 압력은 강체판-빙하 충돌 사이에서 발생하는 반력에 해당 시간의 빙하 면적을 나누어 계산하였다. 빙하 면적은 계산의 편의성을 위해 충돌 시간 동안 빙하와 강체판 사이의 실제 접촉 면적 대신 빙하의 이동 거리에 따른 투영 면적을 사용하였다.

ISO 19906에는 극지방에서 측정하여 얻은 p = 3.5A^-0.7의 빙하의 압력-면적 곡선이 명시되었으며, Ritch et al.(2008)은 CCGS (Icebreaker Canadian Coast Guard Ship) Terry fox에서 빙 충돌로부터 발생하는 국부 압력 실측 데이터를 기반으로 p = 3.5A^-0.56의 압력면적 곡선을 제시하였다. 일년생 빙의 압력-면적 곡선으로써 Palmer(2013)는 Canadian Standards Association(CSA)과 ISO의 관계식을 결합하여 p = 4.8A^-0.5을 제시하였다. Fig. 6에는 Fig. 5의 충돌 해석으로부터 얻은 반력-충돌 거리 곡선을 ISO 19906, Ritch et al.(2008), Palmer(2013)에서 제시한 결과와 비교하여 나타내었다. 강체판-빙 충돌 해석에는 파단 기준 식 (4)를 적용하였다. 식 (4)는 실제 빙 재료의 물리적 거동을 고려하지 않고 단지 빙 재료 파단을 모사하기 위해 제시되었으며, 사용자의 경험적 기준 또는 실측(실험) 데이터와 비교를 통해 교정된다. 따라서 본 연구에서는 ISO 19906, Ritch et al.(2008), Palmer(2013)와 수치 해석으로부터 도출한 반력-충돌거리 곡선의 비교를 통해 파단 기준의 초기 파단 변형률 ε₀의 교정을 수행하였다. 80mm의 요소 길이로 빙하를 구성할 때 초기 파단 변형률이 0.12의 값을 가진다면 기존 연구와 유사한 결과를 얻을 수 있었다(Fig. 6). 요소 크기 민감도를 줄이고 그 외의 다른 요소 크기와 초기 파단 변형률로 발생할 수 있는 해석 결과의 불확실성을 제거하기 위해 이후에 수행하는 충돌 해석에서도 빙하 요소 크기 80mm, 초기 파단 변형률 ε₀=0.12를 적용한다.

Fig. 6.

Comparison of reaction force-crushing distance curves

3. Case study

여기서는 상온과 저온(-50℃) 환경에 놓인 보강판-빙하의 충돌 모사를 위해 ABAQUS/Explicit을 이용한 수치 해석을 수행하였다. NORSOK Standard(2004)에서 규정한 Shared-energy design을 적용하여 빙하와 보강판 모두 에너지 발산이 발생하도록 하였다. 그러므로 두 구조물의 거동을 적절히 모사할 수 있고 신뢰할 수 있는 각각의 재료 모델 사용이 요구된다. 2장에서 유효성이 증명된 빙 재료 모델과 파단 기준을 수치 해석 내의 빙하에 적용하고, 보강판에는 등방성 경화 기반의 von-Mises 항복 모델을 적용한다. 본 연구에서는 사고 한계 상태 관점에서 빙 충격 하중의 상호 작용으로 보강판에서 발생 할 수 있는 강재의 파단 거동을 예측 하였다. 이를 위해 Nam et al.(2018)에서 제시한 연성-취성 파단 예측을 위한 변형률 에너지 밀도, w (SED, Strain energy density) 파단 기준을 적용하였다. SED 파단 기준은 ABAQUS/Explicit의 사용자 서브루틴 VUSDFLD를 통해 이식하였다.

3.1 빙하 - 보강판 모델링

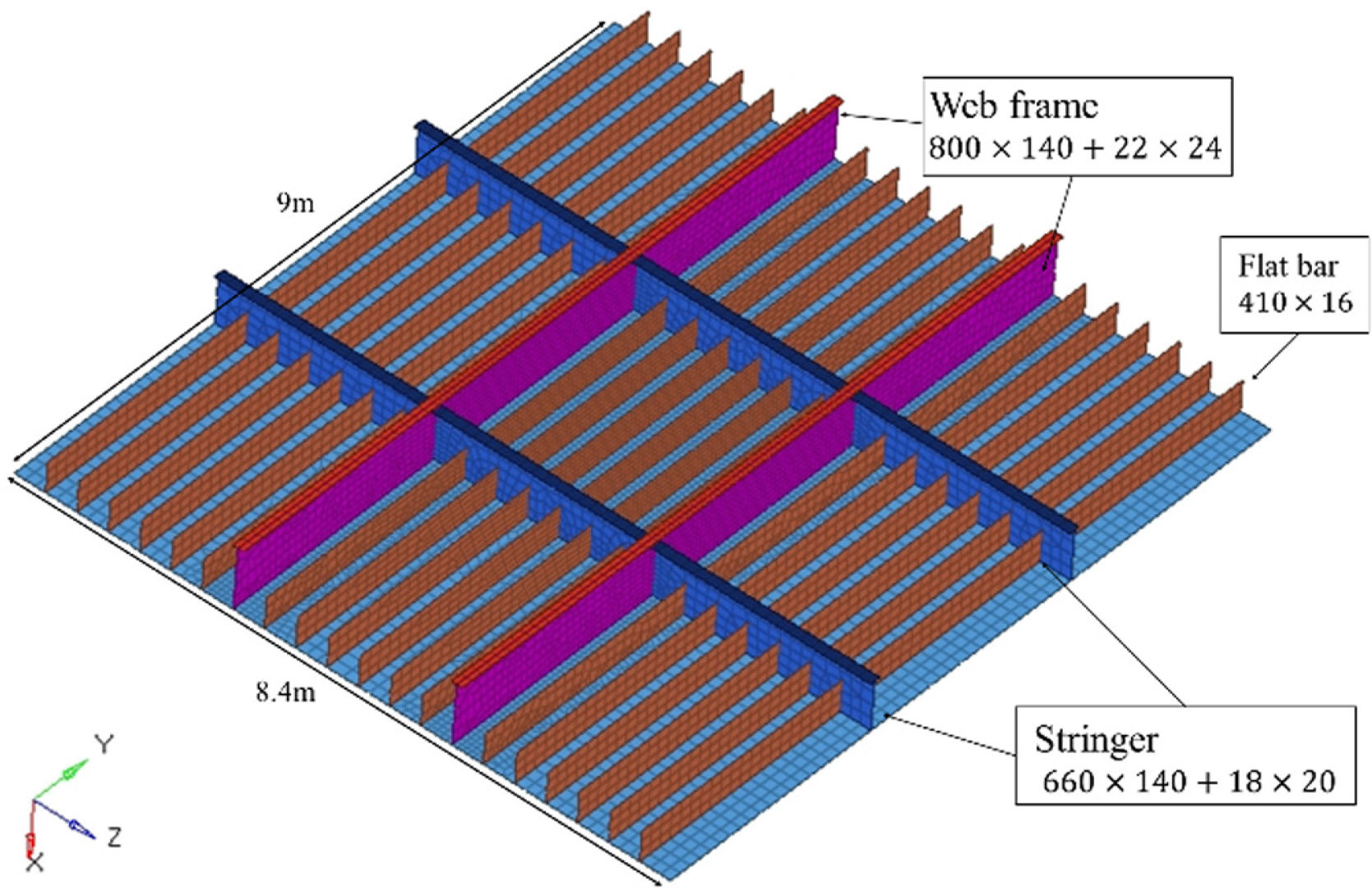
본 연구에서는 피충돌 구조물로써 격자 구조의 보강판을 모델링 하였다. 보강판 모델링을 위해서 Kõrgesaar et al.(2018)을 참고하였다. Kõrgesaar et al.(2018)은 FSICR 및 IACS Polar Class 좌굴 요구 사항을 준수하여 Table 2에 명시한 치수로 Flat bar, Web frame, Stringer로 구성된 격자 구조물을 모델링 하였다(Fig. 7 참고). 보강판의 너비는 8.4m, 높이는 9m이며 Hull plate의 두께는 23.5mm이다. Fig. 7에 나타낸 Flat bar, Stringer, Web frame 간격은 각각 0.4m, 3m, 2.8m이다. 격자 구조물의 모델링에는 S4R(4절점 감차 적분 쉘 요소)를 사용하였으며, S4R은 두께 방향으로 5개의 적분점을 갖는다. 빙하와 직접적으로 접촉하는 보강판의 중앙부는 약 70mm의 요소 길이로 모델링 하였으며, 그 외에는 계산의 효율성을 위해 약 150mm 길이의 비교적 큰 요소로 모델링 하였다.

Table 2.

Scantlings of the stiffened structure

Fig. 7.

Finite element model of the stiffened structure

빙하의 형상은 구(Sphere) 형상을 적용하였다. 빙하의 반경은 1.8m이며 평균적인 충돌 속도의 범주에 기반하여 2m/s의 속도를 빙하에 부여하였다. 빙하는 C3D8R 요소를 사용하여 모델링 하였다. 앞선 2장의 빙 재료 모델 및 파단 기준의 교정 과정에서 쓰였던 빙 요소 길이 약 80mm와 초기 파단 변형률 ε₀=0.12 적용하였다. 빙하와 보강판 사이에 사용된 마찰 계수는 0.15이며, 충돌 시간은 0.6초로 설정하여 두 물체간의 에너지 발산이 충분히 발생 할 수 있도록 하였다. 빙하-보강판의 유한요소 모델링, 경계조건 및 충돌 시나리오는 Fig. 8에 나타내었다.

Fig. 8.

Iceberg-stiffened structure FE modelling

3.2 재료 특성치

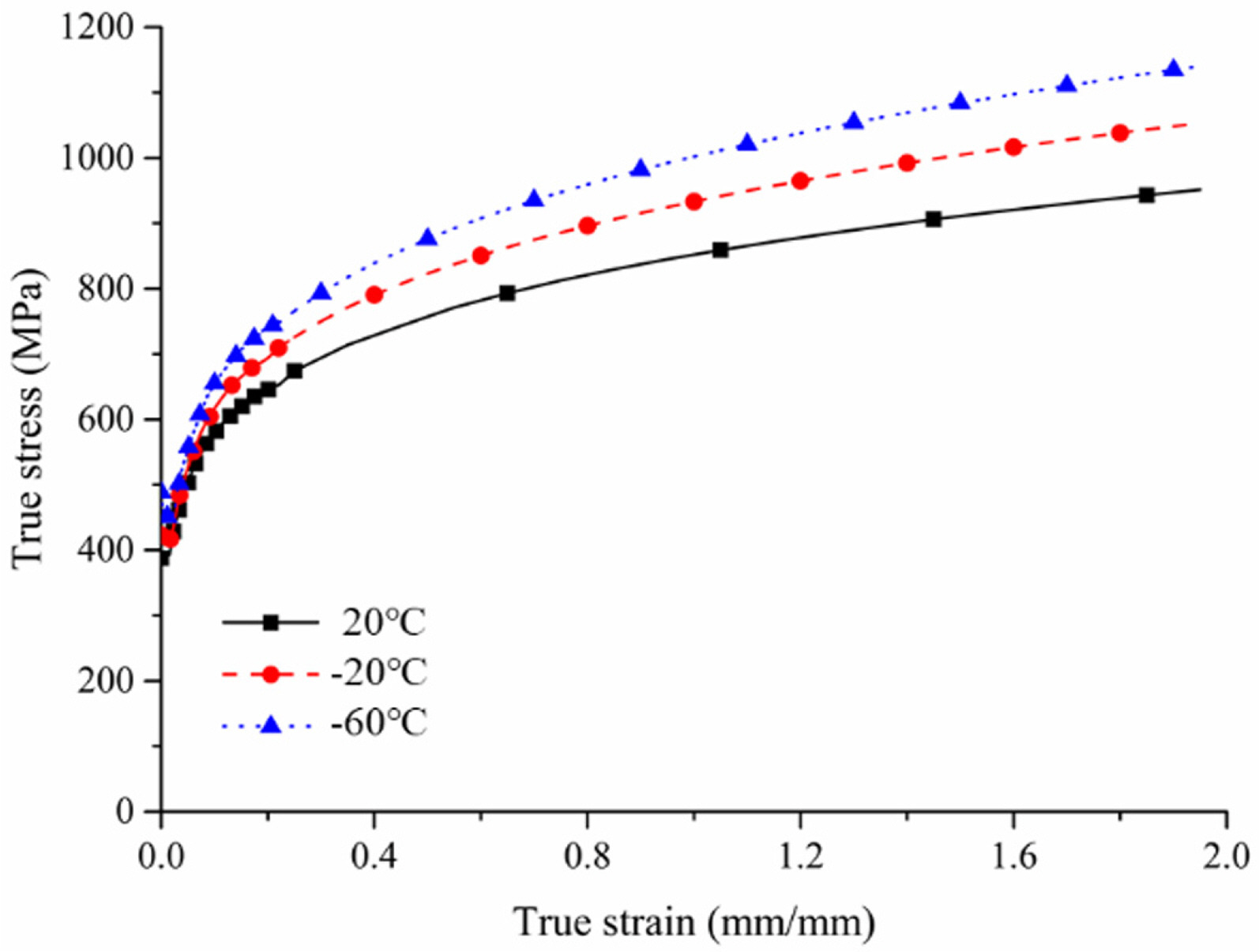
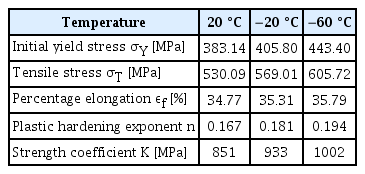
다른 환경 온도에 놓인 구조물의 거동을 비교하기 위해서 각 환경 온도에 맞는 재료 특성치의 정의가 필요하다. 그러므로 상온의 재료 특성치와 보수적으로 가정한 극지방의 환경 온도(-50℃)에서의 재료 특성치를 수치 해석에 적용하였다. 본 논문에서는 대표적인 조선 및 해양구조물 저온 강재 DH36의 기계적 특성치를 보강판의 강재로써 사용하였다. 이를 위해 Park et al.(2015c)의 온도별 준정적 단축 인장 실험 데이터를 참고하였다. Fig. 9와 Fig. 10은 각각 DH36강재의 공칭응력-공칭변형률 곡선과 진응력-진변형률 곡선을 보여주고 있으며 수치 해석에는 진응력-진변형률 곡선을 적용하였다. 본 연구에서의 목표 온도인 -50℃의 재료 특성 치는 ABAQUS/Explicit 프로그램 내에서 -20℃와 -60℃ 진응력-진변형률 곡선 사이의 데이터를 내삽하여 적용된다. Table 3에 DH36 강재의 온도별 기계적 특성치를 제시하였다.

Fig. 9.

Engineering stress-strain curves of DH36 steel, reproduced from Park et al.(2015c)

Fig. 10.

True stress-strain curves

Table 3.

Material properties and hardening parameters of DH36 steel

빙 재료의 경우, 온도에 따라 변하는 빙 재료의 압축 강도는 다음 식 (5)와 같이 표현될 수 있다(Liu et al., 2011).

(5) f(p,J2)=J2−(a0(T)+a1(T)p+a2(T)p2)

식 (3)의 상수 a₀, a₁, a₂를 온도의 함수 a₀ (T), a₁ (T), a₂ (T)로 변형 시켜 빙 재료의 온도에 따른 압축 강도 변화를 나타낼 수 있다. 하지만 이번 수치 해석에는 온도에 따른 빙 재료 특성치 변화를 고려하지 않는다. 이는 온도에 따른 재료 모델 상수의 변화를 증명할 수 있는 실험 결과가 충분하지 않으며, 또한 다른 환경 온도에 노출된 강재 구조물이 동일한 하중 조건을 갖기 위함이다. 일반적으로 온도 감소와 비례하여 빙 재료의 압축 강도는 증가하는 것으로 알려져 있다(Petrovic, 2003).

4. 해석 결과

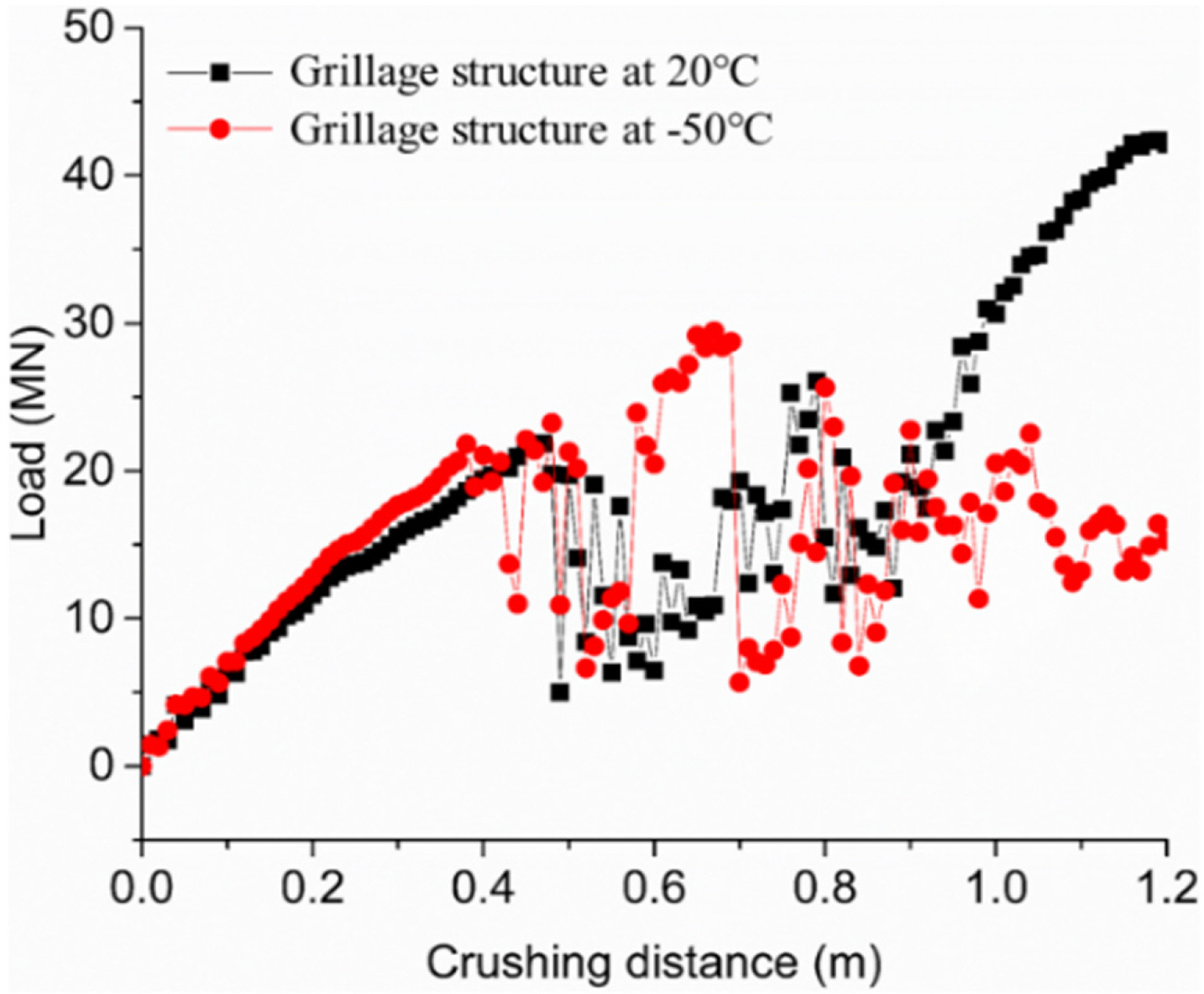
Fig. 11의 검은색, 빨간색 곡선은 각각 상온과 저온 -50℃에 노출된 보강판에 빙하의 충돌 거리에 따라 발생하는 하중 이력을 보여주고 있다. 그림에서 볼 수 있듯이 충돌 초기에 하중은 충돌 거리에 비례하여 비교적 일정하게 증가하다 어느 시점에서부터 빙하의 파단이 발생하면서 보강판이 받는 하중은 큰 변동을 보인다. 저온에서 강재의 기계적 특성치가 증가하면서 보강판의 하중 저항력도 증가하기 때문에 상온보다 저온의 환경에서 빙하의 파단이 일찍 발생한 것으로 판단된다. 저온과 달리 상온에서 보강판은 일정 충돌 거리 이후 빙 충격 하중에 저항하지 못하고 큰 변형을 보이면서 하중이 점차 증가되는 것을 볼 수 있다.

Fig. 11.

Load-crushing distance curves of the stiffened structures

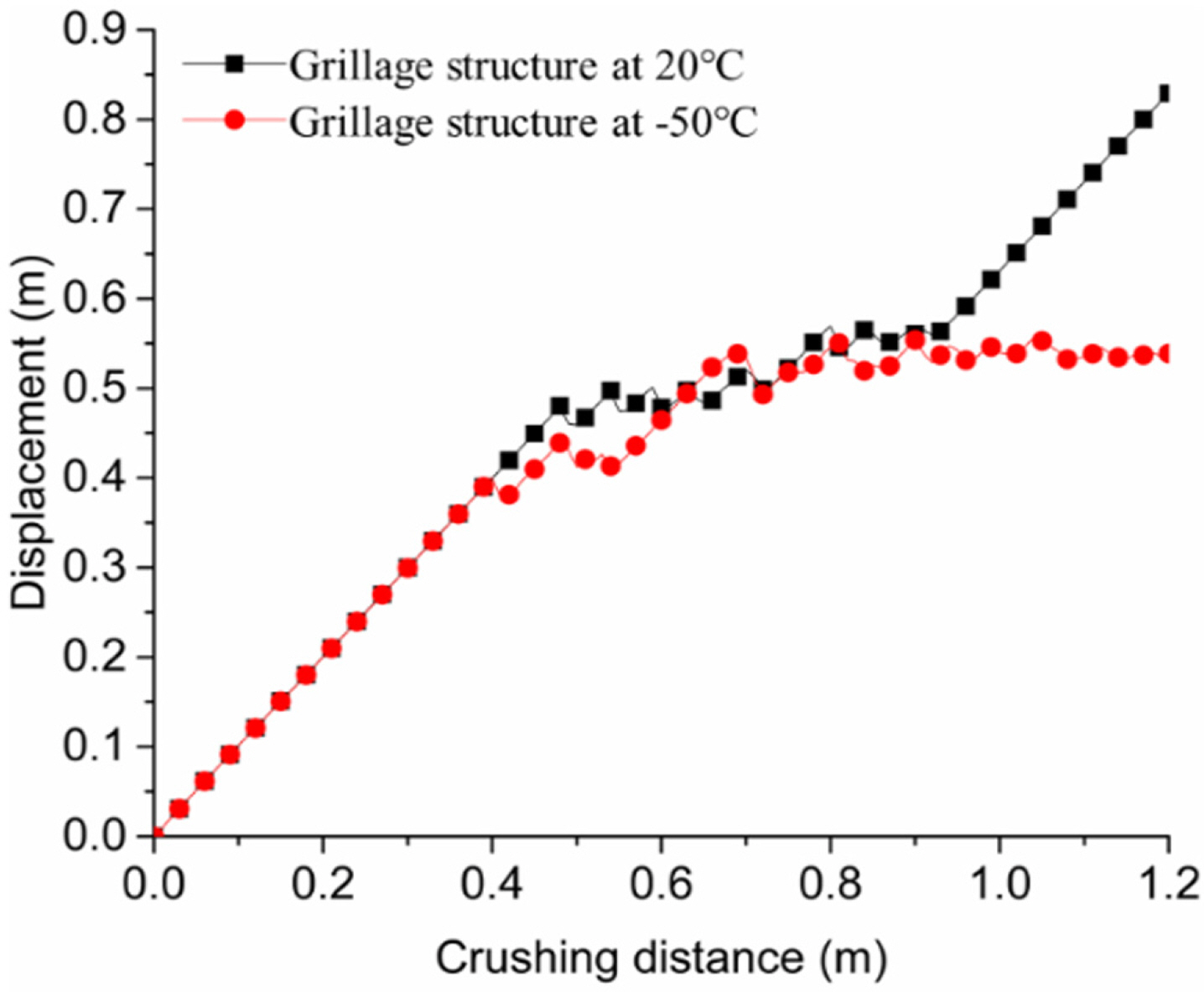
온도에 따른 보강판 구조물의 거동의 차이는 Fig. 12에서도 확인할 수 있다. Fig. 12는 빙하의 충돌 거리에 따른 Point A(충돌 방향으로 발생하는 보강판 내의 최대 변위점, Fig. 13 참고)의 변위를 보여주고 있다. 상온에 노출된 보강판은 충돌 거리 약 0.5m까지 충돌 거리와 비례한 변위를 가지며, 이후 빙하에 파단이 발생하면서 변위의 불규칙적 변화가 나타난다. 상온의 보강판의 경우 충돌 거리 약 0.93m 이후에는 다시 충돌 거리와 비례하는 변위를 갖게 되는데 이 역시 위에서 언급한 것처럼 보강판의 하중 저항력의 감소가 원인으로 예상된다. Fig. 13에는 보강판-빙하 충돌 시뮬레이션의 예로써 충돌 거리에 따른 보강판과 빙하의 거동을 나타내었다.

Fig. 12.

Displacement-crushing distance curves at point A for each stiffened plate

Fig. 13.

Numerical simulation of iceberg-stiffened structure interaction (target temperature –50 °C); (a) Crushing distance = 0 m (b) Crushing distance = 0.6 m (c) Crushing distance = 1.2 m; Point A indicates the middle of the plate, where the magnitude of displacement shows the maximum value

Fig. 14에는 상온 및 저온의 보강판에서 발생하는 등가 소성 변형률을 나타내고 있다. 상온의 경우, 충돌 초기 대부분의 소성 변형은 보강판의 중앙부에 위치한 Flat bar에서 발생한다. 시간이 지나면서 충돌 거리 약 0.3m에서부터 Web frame과 Stringer 경계 조건 부근의 양 끝단에 좌굴이 발생한다. 좌굴 발생 이후 빙하와 접촉하는 Hull plate의 중앙부에 국소적 변위의 큰 증가를 볼 수 있다. 이러한 현상은 초기에 충돌 하중을 견디던 Flat bar의 하중 저항력 감소가 Web frame과 stringer의 좌굴 정도를 심화시키고 그 결과 Hull plate에 작용하던 막 응력의 감소 때문에 발생되는 것으로 추측된다. -50℃에서 보강판의 거동도 상온의 경우와 매우 유사하다. 하지만 온도의 영향으로 증가된 강재 특성치로 인해 보강판의 하중 저항력이 증가하면서 발생하는 변위의 정도는 상대적으로 감소하였다. 또한 여기서 주목해야 할 점은 최대 등가 소성 변형률의 발생 지점이다. 막 응력의 감소로 Hull plate에서 최대 소성 변형률이 발생한 상온의 보강판과 달리, 저온의보강판에서 최대 소성 변형률은 Flat bar와 Hull plate의 접합부에 위치하게 된다.

Fig. 14.

The structural response at target temperature 20 °C (a) and −50 °C (b). Contour shows the distribution of equivalent plastic strain at the end

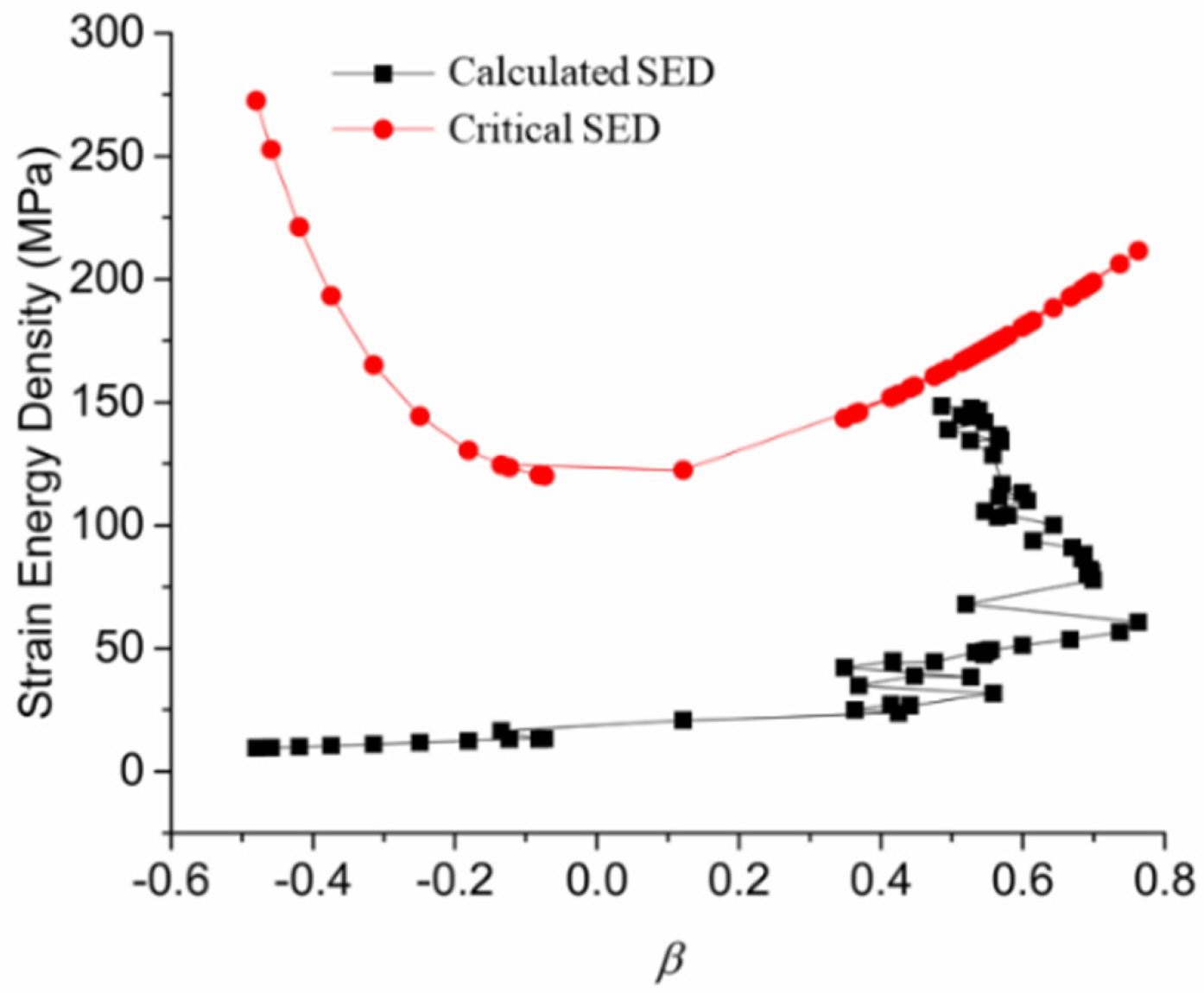
본 연구에서는 사고 한계 상태 설계의 관점에서 빙 충격 하중으로 인해 보강판에서 발생할 수 있는 파단 거동을 조사하기 위해 Nam et al.(2018)에서 변형률 에너지 밀도 파단 기준을 적용하였다. Nam et al.(2018)은 쉘 요소를 이용한 연성-취성 파단을 예측하기 위해 공률 소성(Porous plasticity) 기반의 GTN(Gurson-Tvergaard-Needleman) 연성 파단 모델(Tvergaard and Needleman, 1984)과 최대주응력 기반의 RKR(Ritchie-Knott-Rice) 취성 파단 모델(Ritchie et al., 1973)을 결합하여 변형률 에너지 밀도의 값으로 교정한 파단 기준이다(자세한 SED파단 기준 설명은 참고문헌 참조). Fig. 15에 Nam et al.(2018)에서 제시한 DH36 강재의 온도별 최대 변형률 에너지 밀도를 도시하였다.

Fig. 15.

Fracture loci w_c(β) at temperatures (reproduced from Nam et al., 2018)

β는 변형률 증가율로써 평면 응력 조건내의 면내 최소/최대 주변형률 증가율의 비다. 비례 하중 경로를 가정했을 때 단축 인장 β = -0.5, 평면 변형 인장 β = 0.0, 등 2축인장 β = 1.0의 값을 갖는다. Fig. 15에서 볼 수 있듯이 온도가 감소하면서 국소적 취성 파단이 증가함에 따라 최대 변형률 에너지 밀도가 감소하며, 각 온도에서는 평면 변형 인장 조건 시 최소 임계값을 갖는 것을 볼 수 있다.

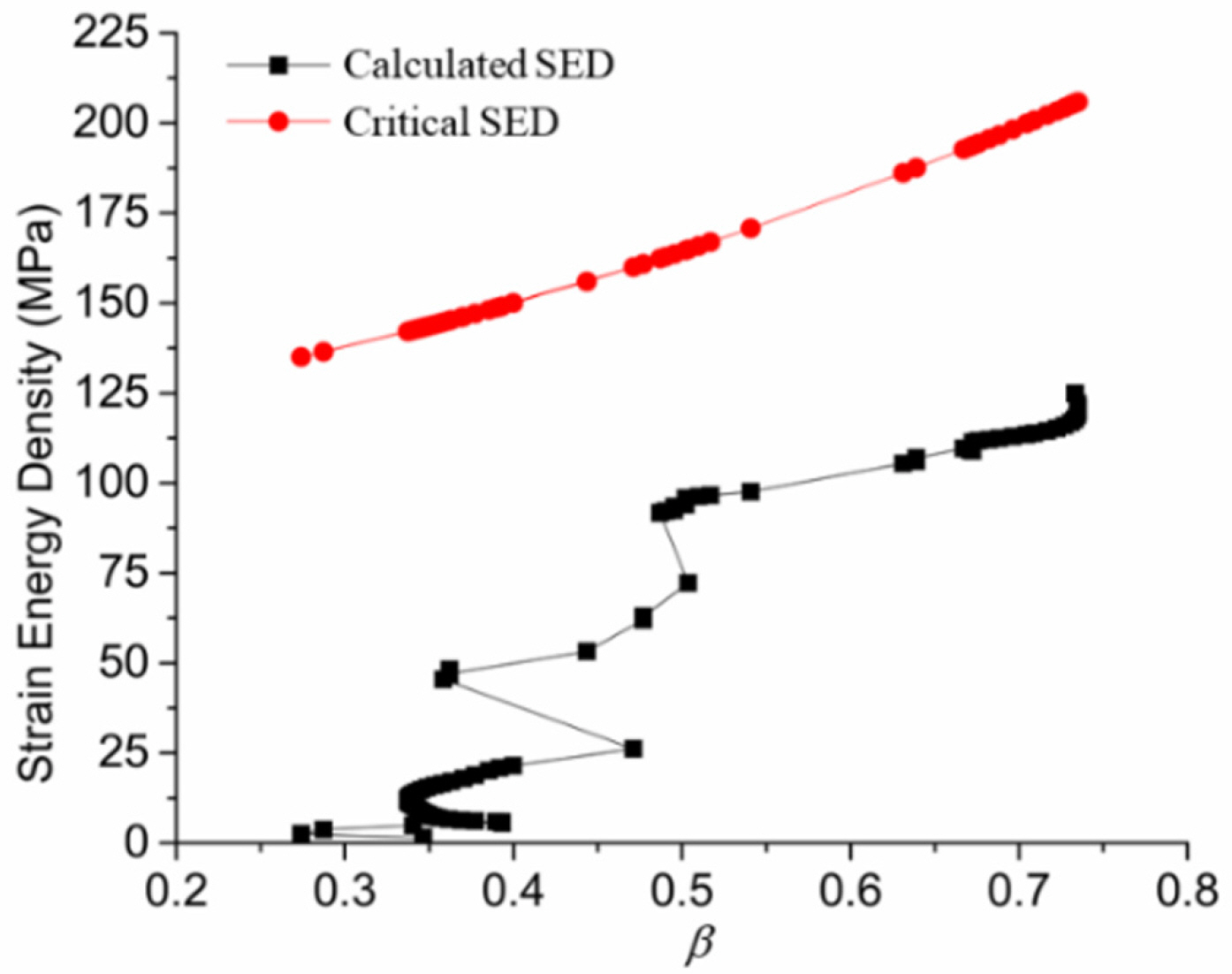
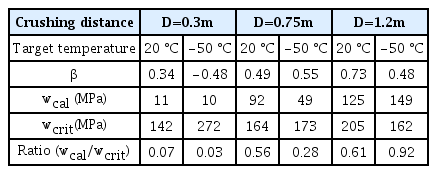
각 온도별 보강판 내 빙 충돌 하중에 따른 변형률 에너지 밀도의 이력을 Fig. 16과 Fig. 17에 나타내었다. 변형률 에너지 밀도의 이력은 최대 소성 변형률을 갖는 요소에서 도출되었다(상온 보강판의 중앙부 Hull plate 요소, 저온 보강판 중앙부의 Flat bar-hull plate 접합부 요소), Hull plate 요소는 충돌 초기부터 2축 인장(β > 0.0)이 작용하고 최종적으로 β = 0.73 갖는다. Flat bar-hull plate 접합부에서 초기에는 단축 인장 (β = -0.5)에 가까운 하중 경로를 보이지만 최종적으로 2축 인장 하중 (β = 0.48)의 상태에 도달한 것을 볼 수 있다. Table 4에는 조사한 요소가 갖는 하중 경로, 변형률 에너지 밀도(w_cal)의 값을 요약 정리하였다. 임의의 충돌 거리에서 요소가 갖는 변형률 에너지 밀도의 이력은 각 보강판의 국소적 변형 발달 속도를 보여주고 있다. 상온의 보강판은 충돌 거리 0.3m에서 0.75m 사이에 급격한 변형률 에너지 밀도의 증가를 보여주는데 이는 앞에서 예측한 바와 같이 Flat bar, Web frame, Stringer의 하중 저항력 감소가 이른 시간 Hull plate 내 국소적 변형률 집중을 야기한 것으로 사료된다. 저온의 보강판은 충돌 거리 0.75m 이후의 급격한 증가를 보이는데 저온에서 증가된 막 응력의 효과로 비교적 늦은 시간에 변형률 집중이 발생한 것으로 판단된다. 본 연구에서 수행한 보강판-빙 충격 하중 상호작용의 수치 해석의 결과는 두 보강판 모두 파단이 발생하지 않았지만 저온의 보강판의 한 요소가 갖는 w_cal/w_crit의 최종 비는 0.92로써 파단 기준의 임계값에 매우 근접한 것을 볼 수 있다.

Fig. 16.

The evolution of strain energy density investigated in the stiffened structure at 20 °C

Fig. 17.

The evolution of strain energy density investigated in the stiffened structure at −50 °C

Table 4.

The evolution of w_cal/w_crit where w_cal and w_crit are the calculated SED and the critical SED in the target element, respectively

5. 토론 및 결론

기존의 연구(Ehlers and Østby, 2012; Park et al., 2015b)는 피충돌 구조물의 내충돌 성능의 평가에 있어 충격 하중으로부터 피충돌 구조물이 흡수하는 에너지 흡수량의 크기를 주요한 판단 기준으로 여겼다. 즉, 같은 하중 조건에서 더 큰 에너지 흡수량을 갖는 피충돌 구조물의 내충돌 성능이 더 우수하다고 간주한 것이다. 이 연구들에서는 NORSOK standard에서 규정한 Ductility design을 기반으로 각각 상온과 영하의 온도에 놓인 선박에 동일한 하중을 부여한 충돌 해석을 수행하였다. 그 결과로써 저온에서 증가하는 강재의 특성(또는 에너지 흡수량)으로 인해 저온에서 구조물의 내충돌 성능이 증가한다고 판단하였다. 하지만 본 연구에서 수행한 수치 해석의 결과, 저온에 노출된 보강판은 Fig. 11-17에서 보인 바와 같이 상온 환경의 보강판과 비교하여 상대적으로 낮은 하중과 작은 변위를 갖음에도 불구하고 변형률 에너지 파단 기준 관점 더 높은 파단 가능성을 가진 것을 확인하였다.

사고 한계 상태 관점의 구조물 내충돌 성능 예측을 위해 수행되는 수치 해석에서 온도에 따른 강재 특성치와 파단 기준의 정의는 매우 중요하다. 그럼에도 불구하고 일부 연구에서는 북극항로의 환경에 놓인 선박 및 해양구조물의 내충돌 성능 평가의 수치 해석에 있어서 상온의 강재 특성치만을 적용하거나 저온에서 발생할 수 있는 강재의 취성화와 취성 파단의 가능성은 고려하지 않은 순수 연성 파단 모델을 적용하였다. 이런 경우 특정 강재의 기계적 특성치와 연성 파단 모델의 사용은 저온에 노출된 구조물의 내충돌 성능을 과대 평가할 수 있다. 예를 들어, 본 연구에서 사용한 DH36 강재의 경우 준정적 단축 인장조건에서 온도가 감소할수록 기계적 특성치 및 파단 연신률이 증가하면서 에너지 흡수량 증가를 보여준다(Fig. 9). 하지만 Fig. 18에서 볼 수 있듯이 Charpy 충격 실험에서 DH36 강재는 온도가 감소하면서 연성-취성 파단 전이 과정으로 시편의 에너지 흡수량이 감소하는 것을 볼 수 있다.

Fig. 18.

Relationship between energy absorption and specimen temperature of DH36 steel, referred from Min et al. (2012)

Nam et al.(2016)은 DH36 강재의 Charpy 충격 실험에서 저온에서 현저히 감소하는 시편의 에너지 흡수량을 모사하기 위해 연성-취성 파단 모델을 결합하여 수치 해석을 수행하였다. 수치 해석의 결과 저온에서 시편에 발생하는 취성파단의 존재를 증명하고 취성 파단 고려 없이 독립적으로 쓰이는 연성 파단 모델의 한계를 보였다. 이러한 결과로부터 북극항로의 평균 온도 -50℃에 노출된 선박 및 해양 구조물을 구성하는 강재는 그 특성치가 증가되지만 충격 하중으로부터 발생할 수 있는 취성 파단으로 인해 그 에너지 흡수량이 감소할 수 있는 가능성을 추정할 수 있다. 그러므로, 북극항로의 환경에 노출되어 있는 구조물의 설계에 있어 외부의 충격 하중으로부터의 발생 할 수 있는 취성 파단의 가능성을 반드시 고려해야 하며, 수치 해석시 취성 파단 거동을 적절히 모사 할 수 있는 신뢰성 있는 파단 모델의 사용이 필요하다.

본 논문에서는 다른 환경 온도에 놓인 보강판의 빙 충격 하중에 의한 구조적 거동을 비교, 분석하기 위해 상용 유한 요소 해석 프로그램 ABAQUS/Explicit을 이용해 수치 해석을 수행하였다. 그 결과 저온에 노출된 보강판은 증가된 강재의 기계적 특성치 때문에 상대적으로 더 작은 충격 하중과 변위에도 불구하고 Nam et al.(2018)에서 제시한 SED 파단 기준의 관점으로 파단의 위험에 더 노출되어 있는 것을 확인할 수 있었다.

Fig. 19에는 실제로 발틱해와 북극항로에서 운항하던 선박에서 빙 충돌로 발생한 용접부의 파단을 나타내고 있다. 선박 및 해양 구조물은 많은 보강재와 용접부로 구성되는데, 이러한 용접부(접합부)에서 상당한 응력과 변형률 집중이 발생한다. 이외에도 용접 열 영향부에 초기 항복 응력 수준의 잔류 응력이 존재하게 된다. 이러한 요소들은 사고 시 외부의 충격으로부터 강재가 파단 임계값에 더 쉽게 도달할수 있도록 한다. 북극항로를 운항하는 구조물의 구조적 안전성을 정확하게 예측하기 위해서는 파단에 취약한 용접부와 용접 열 영향부의 파단 가능성을 설계 단계에서 고려해야 하며 향후 저온에서 용접부 및 용접 열 영향부의 강재 특성치 및 거동을 파악하기 위한 적절한 실험이 요구된다.

Fig. 19.

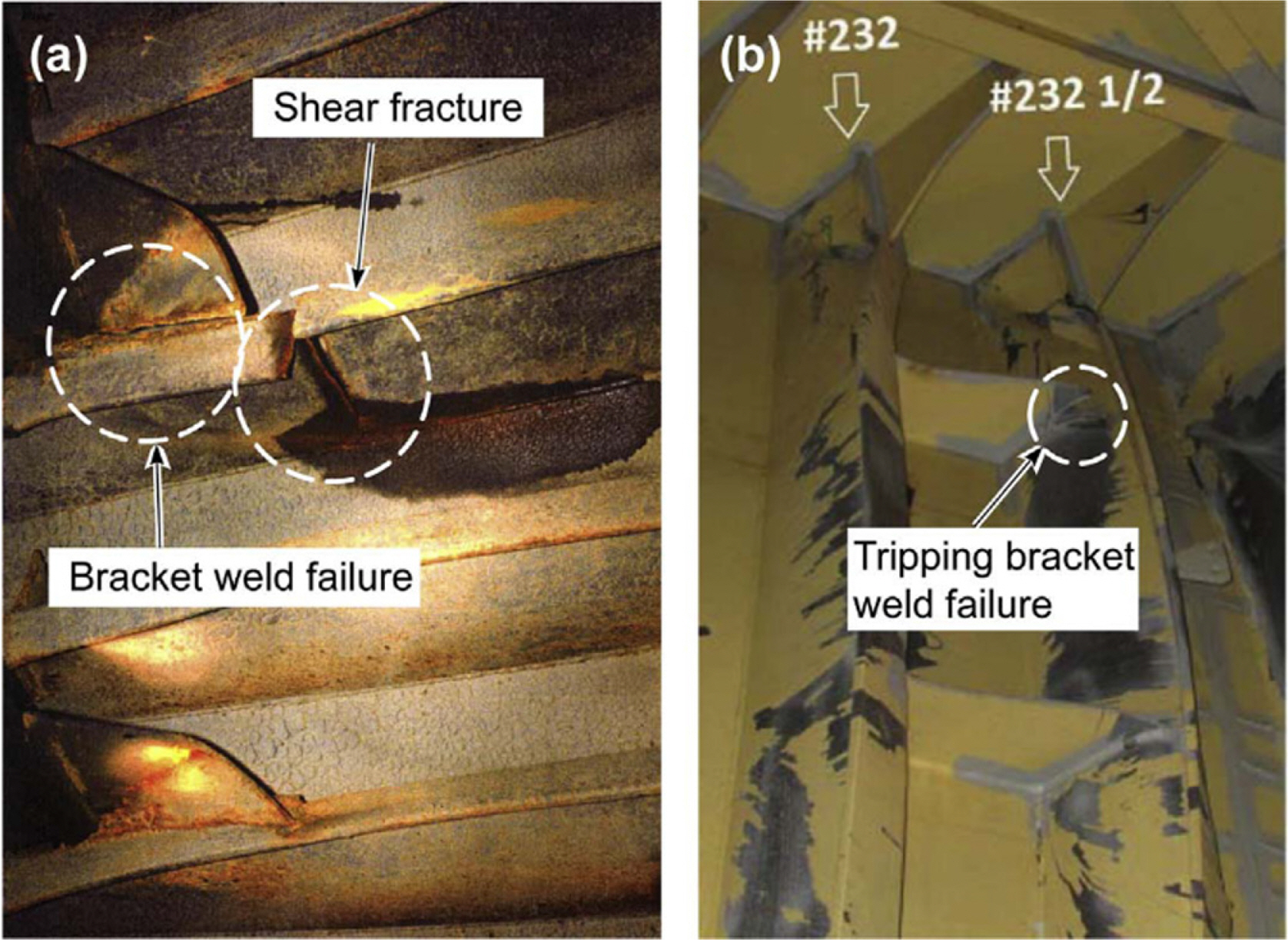
Fracture in plate-stiffener junction due to ice overload, referred from Kõrgesaar et al. (2018)

Article information Continued