유리 섬유 강화 폴리우레탄 폼의 온도 및 변형률 속도 의존 재료 거동 모델링
Modeling of the Temperature-Dependent and Strain Rate-Dependent Dynamic Behavior of Glass Fiber-Reinforced Polyurethane Foams
Article information
Trans Abstract
The purpose of this study was to establish a numerical model of polyurethane foam (PUF) to simulate the dynamic response and strength of membrane-type Liquefied natural gas (LNG) Cargo containment system (CCS) under the impact load. To do this, initially, the visco-plastic behavior of PUF was characterized by testing the response of the PUF to the impact loads with various strain rates as well as PUF densities at room temperature and at cryogenic conditions. A PUF material model was established using the test results of the material and the FE analysis. To verify the validation of the established material model, simulations were performed for experimental applications, e.g., the dry drop test, and the results of FEA were compared to the experimental results. Based on this comparison, it was found that the dynamic response of PUF in dry drop tests, such as the reaction force and fracture behaviors, could be simulated successfully by the material model proposed in this study.
1. 서 론
선체 운동과 화물창 내부 액화 천연 가스(Liquefied natural gas, LNG)와의 공진에 의해 발생하는 슬로싱 현상은 LNG 화물창 내부에 격렬한 유체 운동을 발생시키며 이는 매우 국부적이고 큰 유체 충격압을 유발시켜 LNG 화물 저장 시스템(Cargo containment system, CCS)의 손상을 일으키는 주요 원인이 된다. 따라서 운항 기간 동안 화물창 내부에 발생하는 슬로싱 하중에 대한 CCS의 파손 방지 설계는 멤브레인형 LNG CCS 설계에 있어 핵심 이슈가 되고 있다(Lee et al. 2010). 지금까지 수치해석을 통해 슬로싱에 대한 CCS의 동적 강도를 정량적으로 평가하기 위한 많은 시도는 유체구조 연성(Fluid structure interaction, FSI) 현상, 충격 하중하에서 CCS 구성 재료에 대한 동적 거동 규명 등과 같은 난제로 인해 어려움을 겪고 있는 것이 사실이다.
일반적으로 멤브레인형 LNG CCS는 정⋅동적 하중하에서의 구조 성능과 더불어 자연 기화율(Boil off rate, BOR) 최소화 등과 같은 기능적 요구 조건을 만족시키기 위하여 단열재와 구조재를 적층한 샌드위치 복합 구조로 설계되며 단열재로 낮은 열전도율, 우수한 하중 지지능과 더불어 높은 에너지 흡수능을 가지는 폴리우레탄 폼(Polyurethane foam, PUF)이 주로 사용된다. 특히, LNG CCS에 사용되는 PUF는 강도 확보를 위해 유리 섬유로 강화된 재료를 사용하고 있으며, 최근에는 CCS의 BOR (Boil off rate) 설계 조건에 따라 다양한 밀도의 PUF가 적용되는 추세이다. 일반적으로 발포 재료의 물성은 밀도, 변형률 속도 및 미세 구조와 같은 변수에 따라 달라지므로(Gibson and Ashby, 1997) 멤브레인형 LNG CCS의 강도를 정확하게 평가하기 위해서는 극저온 환경에서 이들 변수의 영향을 규명하는 것이 필요하다. 따라서 LNG CCS의 동적 강도를 유한요소해석을 통해 정량적으로 평가하기 위해서는 PUF의 밀도, 하중 속도 그리고 온도가 재료의 동적 거동 특성에 미치는 영향을 규명할 수 있는 재료 모델 개발이 선행되어야 한다. 지금까지 몇몇 연구자들에 의해 다양한 조건에서 PUF의 기계적 특성을 규명하기 위한 실험적 연구가 있었다. Jang et al.(2013)은 밀도가 130kg/m3과 210kg/m3인 강화 PUF를 대상으로 극저온 열전달 특성과 열 수축 변형 거동을 실험적으로 연구하였으며, Lee et al.(2007a)은 LNG CCS용 강화 PUF에 대하여 상온에서의 동적 거동 특성을 정적 기계 시험과 Dry drop 시험 기법을 이용하여 분석하였다. 또한, Park et al.(2014)은 극저온용 단열재에 대하여 정적 압축 시험을 통하여 온도 의존 압축 거동을 평가하였다. 재료 모델링의 경우, 자동차용 폼 재료에 대하여 상온에서의 변형률 속도에 따른 재료 거동을 수치적으로 모사하기 위한 시도가 있으며(Kim and Choi, 1996), LNG CCS용 PUF를 대상으로 상온 정적 하중 조건에서 기계적 거동을 물리적으로 표현하기 위한 이방성 점탄소성 손상 모델에 대한 연구가 있었다(Lee et al., 2012). 하지만, 극저온 환경에서의 충격 하중 조건에서 PUF 동적 거동에 대한 실험적 연구와 이를 수치적으로 모사하기 위한 재료 모델에 대한 연구는 거의 없는 실정이다.
본 연구의 목적은 극저온 환경에서 충격 하중을 받는 LNG CCS의 동적 응답과 강도 특성을 정량적으로 평가하기 위한 PUF의 수치 모델링 기법을 정립하는 데 있다. 이를 위해 다양한 밀도를 가지는 PUF에 대하여 상온과 극저온 조건에서 PUF의 점탄소성 거동 특성을 하중 부가 방향과 변형률 속도에 따른 정⋅동적 시험을 통해 규명하였으며, 시험 결과를 이용하여 PUF의 동적 거동을 지배하는 인자들의 영향을 수치적으로 모델링할 수 있는 PUF 재료 모델을 개발하였다. 개발된 PUF의 재료 모델을 검증하기 위해 Dry drop 시험을 수치적으로 시뮬레이션하여 그 결과를 시험과 비교한 결과, 본 연구에서 제안된 PUF의 재료 모델을 이용한 수치 해석이 실험으로 계측된 반력, 변형 등의 동적 응답 특성과 시험체의 파괴 거동을 잘 예측하였다.
2. 재료 시험
2.1 시험 방법 및 조건
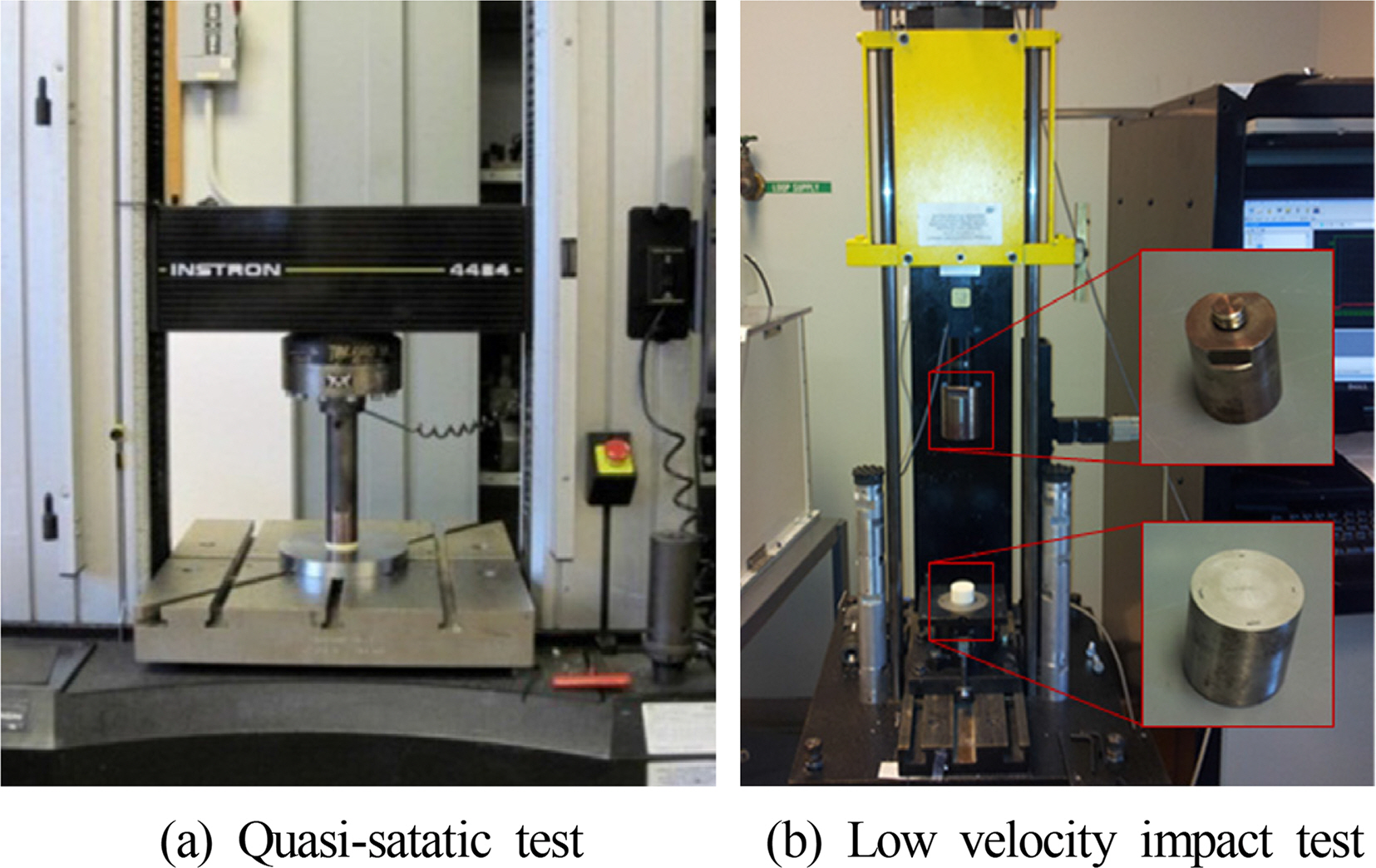
멤브레인형 LNG CCS에서의 PUF는 사용기간 동안 주로 압축 하중을 받기 때문에 상온과 극저온에서 PUF의 변형률 속도 의존 응력-변형률 관계를 얻기 위하여 준정적 압축 시험과 충격 시험을 수행하였다. 본 연구에서 대상으로 한 PUF의 밀도는 40kg/m3, 130kg/m3 그리고 210kg/m3(이후, D40, D130, D210으로 표기)로 3가지 종류이며, 발포제는 HFC-245fa이다. 밀도 D40 시험편은 유리 섬유가 함유되지 않았으며, 그 외 시험편은 발포시 무방향 유리 섬유 다발을 이용하여 10wt%의 유리 섬유로 강화되었다. 시험편은 Fig. 1과 같이 각각 PUF의 발포 방향(Z로 표기)과 유리 섬유가 강화된 발포 수직 방향(XY로 표기)으로 직경(D)과 높이(H)가 각각 30mm, 20mm인 실린더 형태로 가공하였다. 준정적 압축 시험은 Fig. 2(a)와 같이 44.5kN의 로드셀이 장착된 INSTRON 4484 장비를 이용하여 상온에서 수행하였으며, 실험시 압축 하중 부가 속도 및 최종 압축율은 각각 0.02mm/s와 85%로 설정하였다.
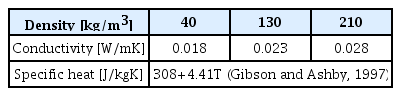
변형율 속도에 따른 동적 강도 특성을 평가하기 위한 저속 충격 시험은 44.5kN의 로드셀 용량을 가지는 INSTRON DYNATUP 9200모델을 사용하였으며, 시험을 위해 Fig. 2(b)와 같이 관통 충격 시험용 텁(Tup)과 엔빌(Envil)을 실린더형 시편의 압축 충격 시험을 위해 수정하여 사용하였다. 저속 충격 시험시 낙하 중량물이 시편을 타격하는 순간의 속도와 에너지는 Table 1과 같다. 시험 장비의 로드셀 용량을 고려하여 각 시험 조건에서 5개의 시편에 대해 낙하 텁이 시편을 타격하는 순간의 변형률 속도가 50s-1, 100s-1 그리고 150s-1가 되도록 타격시 속도를 1.0m/s, 2.0m/s 그리고 3.0m/s로 선정하였다. 충격 시험은 20°C 상온과 통상적인 충격 시험에서 최저 온도 조건인 -196°C 극저온 두 가지 조건에서 실시하였다. 이때, PUF는 폐쇄형 독립 셀(Closed cell) 구조를 가지는 것으로 알려져 있어(Choe et al., 2004) 극저온 시험 조건은 액화 질소에 시험편을 함침시켜 구현하였으며, 각 시편의 액화 수소내 함침 시간은 Table 2의 밀도에 따른 PUF의 열전도도와 액화 질소와 실린더 형태 시편 간의 자유 대류를 고려한 과도 열전달 해석을 통하여 선정하였다. 이때, 시편별 최소 함침 시간은 전체 시편의 온도가 -196°C에 도달하는 시간으로 정의하였다. Fig. 3에 과도 열전달 해석 모델과 이를 통해 평가된 밀도에 따른 각 시편 중앙부의 시간에 따른 온도 변화와 최소 함침 시간을 나타내었다.
2.2 시험 결과
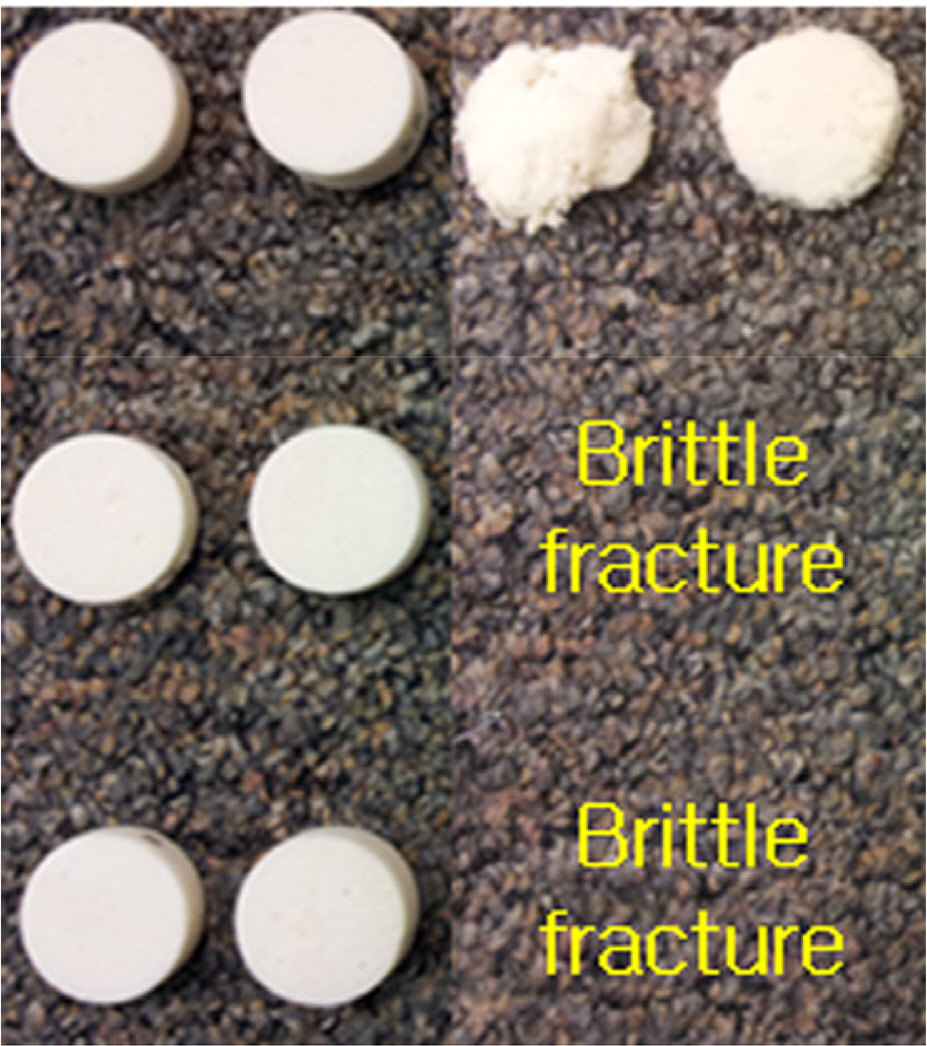
Table 3는 준정적 압축 시험과 저속 충격 시험후 시편의 형상을 도시한 것이다. Table 3와 같이 상온 시험후 시편 형상은 준정적 압축 시험과 충격 시험에서 큰 차이가 없지만 극저온 상태에서는 밀도와 하중 속도에 따라 시편의 파손 양상에 차이가 있다. 특히, 유리 섬유가 함유되지 않은 D40 시편은 극저온에서 재료의 취성 효과에 기인하여 충격 속도 2.0m/s 이상에서 완전히 파손됨을 알 수 있다. 그러나 유리 섬유가 강화된 D130과 D210 시편의 경우 저온에서 하중 방향에 따라 시편 파손 양상에 차이가 발생함을 확인할 수 있다. 즉, 충격 속도 2m/s 이상의 D130과 D210 시편의 경우 발포 방향(Z)으로 채취된 시편이 발포 수직 방향(XY)으로 채취된 시편에 비해 상대적으로 온전한 형태를 가지고 있다. 이는 CCS 설계시 슬로싱에 의한 충격 하중에 대한 저항성을 확보하기 위해서 발포 방향으로 충격 하중을 받도록 PUF를 배치하는 것이 타당함을 의미하는 결과이다.
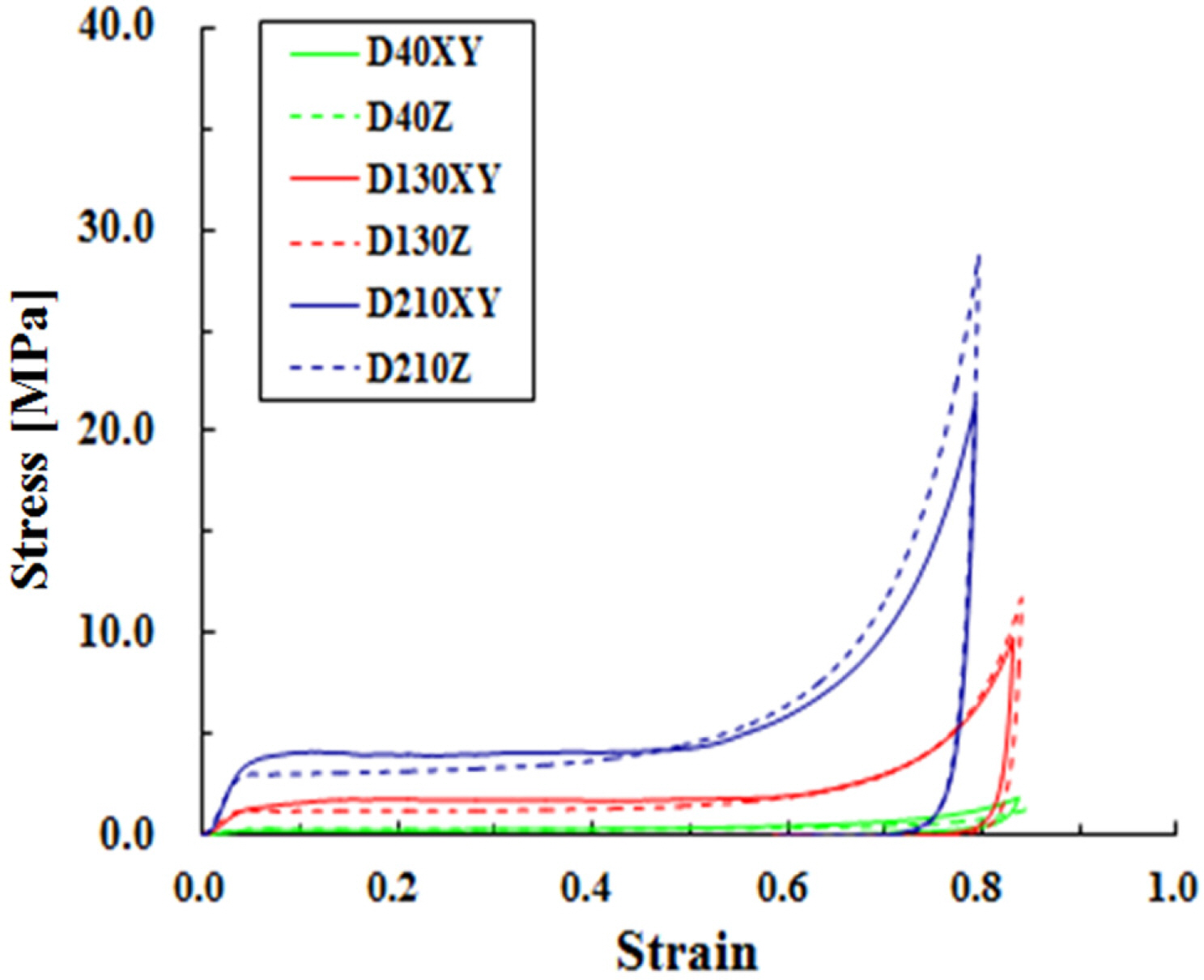
Fig. 4는 준정적 시험을 통해 얻은 밀도에 따른 PUF의 응력-변형률 관계를 도시한 것이다. Fig. 4와 같이 정적 하중하에서 응력-변형률 관계는 탄성(Elastic), 평탄(Flat plateau) 그리고 치밀화(Condensation) 영역으로 구분되는 전형적인 폼 재료의 거동(Zhang et al., 1998)을 가짐을 알 수 있다. 탄성 영역이 끝나는 시점의 응력으로 정의되는 PUF의 항복 응력은 밀도에 비례하여 증가하며, 폼의 발포 방향(Z) 시편과 비교하여 유리 섬유로 강화되어 있는 발포 수직(XY) 방향의 항복 응력이 상대적으로 높다. 그리고 발포된 폼 내부의 기공이 압축 변형에 의해 완전히 압착되기 시작하는 치밀화 개시 변형률은 폼의 밀도가 증가함에 따라 감소함을 하나 하중 방향에는 큰 영향을 받지 않음을 알 수 있다.
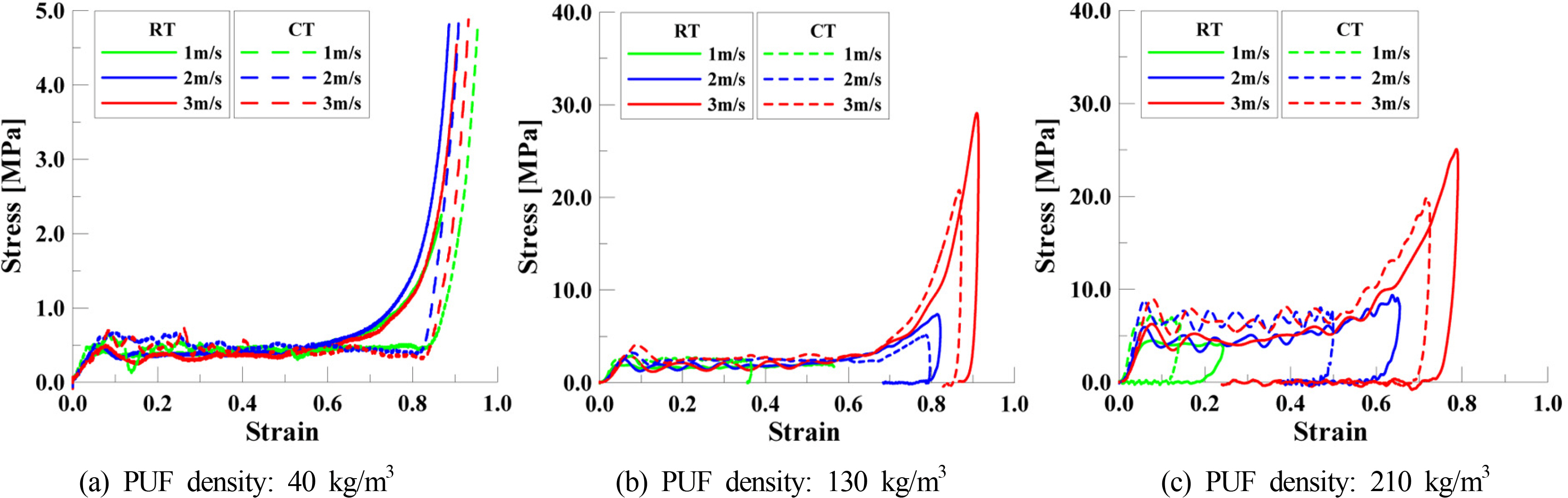
상온과 극저온에서 시편 채취 방향에 따른 충격 시험을 통해 얻은 변위에 따른 하중과 속도의 관계를 이용하여 속도 의존 응력-변형률 관계를 계산하고 이를 각각 Fig. 5와 Fig. 6에 도시하였다. Fig. 5와 Fig. 6과 같이 온도와 하중 속도의 변화에 따라 PUF의 응력-변형률 거동 양상은 준정적 시험과 유사하게 폼 재료의 거동을 유지함을 알 수 있다. 또한, 극저온에서의 변형률 속도 의존 응력-변형률 거동은 실온에서의 거동과 유사한데 이는 PUF의 특성이 극저온에서도 변하지 않음을 의미한다. 각각의 시험 조건에 따른 PUF의 동적 강도 특성을 파악하기 위하여 준정적 및 저속 충격 시험을 통해 얻은 항복 강도와 변형률을 각각 Table 4와 Table 5에 나타내었다. Table 4와 Table 5과 같이 본 연구에서 대상으로 선정한 PUF의 항복 강도는 밀도와 변형률 속도에 비례하여 증가하지만 시험 온도에는 반비례함을 알 수 있으며, 시편 채취 방향에 따른 항복 거동의 차이로부터 재료 이방성을 가짐을 알 수 있다.
이상의 준정적 압축 및 충격 시험 결과를 토대로 멤브레인형 LNG CCS용으로 상용화된 PUF를 대상으로 상온 및 극저온에서 밀도, 시편 채취 방향 및 변형률 속도에 의존하는 재료의 동적거동을 수치적으로 모사할 수 있는 재료 모델링 기법을 제안함으로써 향후 충격 하중하에서 멤브레인형 LNG CCS의 동적 응답과 강도 특성을 유한요소해석을 통해 평가할 수 있는 기반 기술을 확보하고자 하였다.
3. 재료 모델 선정
충격 하중하에서 PUF의 동적 거동을 시뮬레이션하기 위하여 재료 시험 결과와 유한요소해석을 이용하여 PUF의 재료 모델을 선정하였다. 이를 위해 본 연구에서는 유한요소해석 솔버로 LS-DYNA를 활용하였다. 일반적으로 LS-DYNA는 상용 유한요소해석 프로그램으로 외연적 시간 적분법을 활용하여 비선형성이 큰 과도 동적 문제의 시뮬레이션에 적합한 것으로 알려져 있다(LSTC, 2012). 준정적 재료 시험과 저속 충격 시험 결과로부터 대상 PUF는 전형적인 폼 재료의 압축 거동을 가지는 것을 확인하였으므로, 일반적으로 저밀도에서 중밀도까지의 발포 재료에 대하여 변형률 속도에 의존하는 동적 재료 거동을 효과적으로 모사할 수 있는 FU_CHANG_FOAM 모델을 재료 모델로 선정하였다. 특히, FU_CHANG_FOAM 모델은 저속 충격 시험을 통해 얻은 변형률 속도에 따른 응력-변형률 데이터를 직접적으로 입력 가능하다는 장점을 가진다(Croop and Loba, 2009).
3.1 유한요소해석 모델 및 방법
선정된 PUF 재료 모델의 타당성 평가를 위해 Fig. 7과 같이 준정적 및 저속 충격 시험 환경을 수치 모델로 모사하였다. Fig. 7과 같이 3개의 파트로 구성된 수치 해석 모델은 하중을 부가하는 파트 그리고 PUF 시험편을 지지하는 엔빌은 4절점 쉘 요소를 이용하여 강체로 모델링하였으며, PUF 시험편은 하나의 적분점을 가지는 8절점 솔리드 요소(Reduced ingeration element)를 이용하여 FU_CHANG_FOAM 재료로 모델링하였다. 이때, PUF 시험편은 각각 980개와 816개의 노드와 요소로 구현하였다. 또한, 각 파트 간의 접촉부는 면 접촉 조건으로 모델링하였으며, PUF 재료 모델에 따른 재료의 동적 거동 차이를 평가하기 위하여 화물창 구조 안전성 평가시 PUF의 재료 모델로 통상적으로 사용되는 직교 이방성 탄성 모델을 이용한 시뮬레이션 결과와 비교하였다. 하중 조건으로 각각의 시험 조건에 상응하는 중력 방향 속도를 이동 또는 낙하체의 절점에 부여하였다. 이때, 해석 시간을 줄이기 위하여 낙하체가 시편에 충돌하기 직전 상태에 초기 속도를 부여하여 해석을 수행하였다. 또한, 9.8m/s2의 중력 가속도가 전체 수치 해석 모델에 작용하도록 하였으며, 경계 조건은 이동 또는 낙하 파트의 경우 중력 방향 자유도만 허용하는 클램핑 조건을 적용하였으며, 시편을 지지하는 엔빌에 해당하는 모든 절점의 자유도는 구속하였다. 외연적 시간 적분법을 이용한 해석시 안정적인 시간 증분은 통상 음파가 유한요소 모델의 재료 밀도에 의해 결정되는 속도로 최소 크기의 요소를 이동해 지나가는 시간에 의해 결정된다. 따라서, 본 연구에서는 해석시 시간 증분은 안정적인 시간 증분 이하가 되도록 유한요소 해석 솔버에서 자동으로 선정하도록 하였다.
3.2 실험 결과 및 고찰
Fig. 8은 밀도가 130kg/m3인 PUF 시편의 저속 충격 시험과 유한요소해석을 통해 얻은 충격 시작 시점부터 시간에 따른 속도의 변화를 비교한 것이다. 여기서 (+)속도는 중력 방향을 나타내는데, Fig. 8과 같이 충격 속도가 1m/s로 충격 에너지가 상대적으로 작은 경우에는 PUF가 모든 충격에너지를 흡수하여 시험 종료까지 (+)속도 값을 가지는 반면 상대적으로 충격 에너지가 큰 2m/s와 3m/s 시험 조건에서는 충격후 반발에 의해 (-)값으로 속도가 천이됨을 확인할 수 있다. 특히, PUF의 재료 모델에 따른 시뮬레이션 차이를 비교 평가하기 위한 2m/s의 해석 결과의 경우 FU_CHANG_FOAM 재료 모델은 시험 결과와 매우 잘 일치하지만 직교 이방성 탄성 재료 모델의 경우는 실제 시험 결과와 차이가 크게 발생함을 알 수 있다. Fig. 9는 초기 충격 속도가 2.0m/s일 때 유한요소해석과 저속 충격 시험을 통해 얻은 PUF 밀도에 따른 응력-변형률 관계를 비교한 결과이다. Fig. 9와 같이 FU_CHANG_FOAM 재료 모델을 사용한 모든 경우에서 저속 충격 시험 결과와 유한요소해석 결과가 매우 잘 일치함을 확인할 수 있다. 반면, 직교 이방성 재료를 사용한 경우에는 실제 시험 결과와 시뮬레이션 결과에 큰 차이가 발생한다. 이는 본 고에서 PUF의 재료 모델로 선정한 FU_CHANG_FOAM 모델이 동하중 하에서 PUF의 거동을 모사하는데 적합함을 의미한다. 따라서 선정된 PUF 재료 모델을 사용하여 통상적으로 멤브레인형 LNG CCS의 동적 강도 평가를 위한 시험법으로 채택하고 있는 Dry drop 시험(Lee et al., 2007a; Lee et al., 2007b)을 수치적으로 시뮬레이션하고 그 결과를 토대로 PUF 재료 모델이 CCS의 동적 강도에 미치는 영향을 평가하였다.
4. Dry drop 시뮬레이션
4.1 시뮬레이션 모델 및 방법
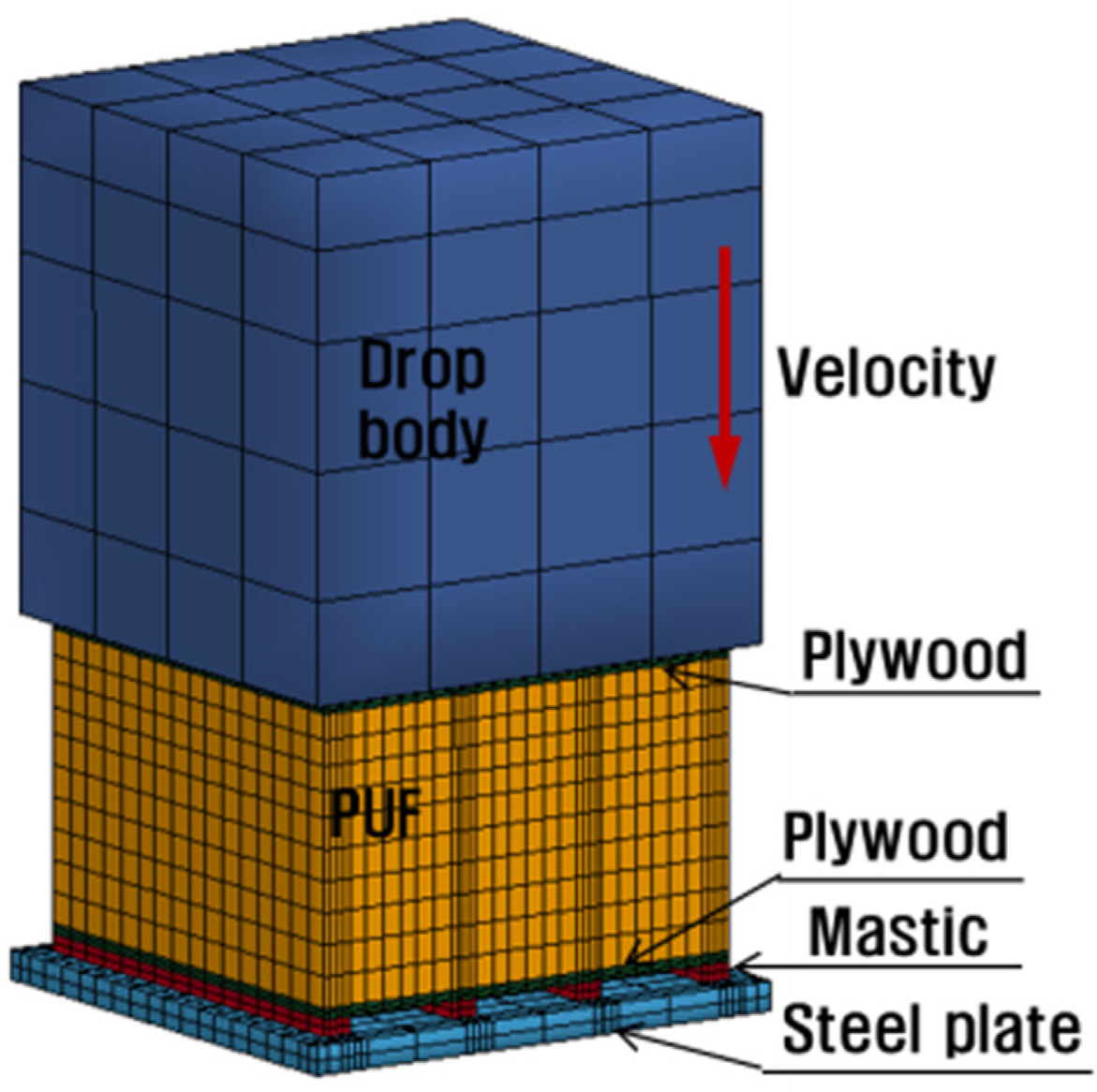
본 고에서 선정된 PUF 재료 모델의 검증을 위해 Dry Drop 시험 환경을 수치 해석으로 모사하고 그 결과를 실험 결과와 비교하였다. Fig. 10은 Dry dorp 시험시 사용한 장비를 도시한 것으로, Fig. 10과 같이 PUF의 에너지 흡수능에 따른 시험체의 동적 거동을 평가하기 위하여 마스틱 하부에서 4,000kN 용량의 로드셀을 이용하여 반력을 계측하였다. Dry drop 시험은 상온에서 수행되었으며, 시험 장비의 로드셀 용량을 고려하여 680kg의 낙하체의 자유 낙하 높이를 150mm에서 950mm까지 변화시켜 시험을 수행하였다. 본 고에서는 Dry drop 시험 중 415mm 낙하 조건에서의 시험 결과를 수치적으로 모사하여 시험으로부터 얻은 동적 거동과 비교 검토하여 선정된 PUF 재료 모델의 타당성을 검증하였다. Dry drop 시험시 시험편의 PUF 밀도는 현재 상용화되어 있는 멤브레인형 LNG CCS에서 주로 사용되고 있는 130kg/m3으로 선정하였다. Table 6은 Dry drop 시뮬레이션에 사용된 단열 패널의 치수 및 구조적 특성을 나타내며 Fig. 11은 유한요소해석 모델을 도시한 것이다. Table 6과 같이 시험체는 4개의 층으로 구성된 샌드위치 복합 구조를 가지며, Fig. 11과 같이 시험체는 15mm 두께의 강판위에 에폭시 계열의 접착제인 마스틱(Mastic)을 이용하여 접착하고 이를 시험기에 고정하였다. 시뮬레이션시 하중 및 경계 조건은 재료 모델 개발을 위한 저속 충격 시험과 동일하게 적용하였다. Table 7은 LS_DYNA를 이용한 유한요소해석시 사용된 각 파트별 재료 모델을 나타낸다. Table 7과 같이 낙하체(노드수 150개, 요소수 80개)와 하부 강판(노드수 1,377개, 요소수 832개)은 강체로, Plywood(노드수 1,785개, 요소수 1,088개)는 직교 이방성 탄성 재료 그리고 마스틱(노드수 1,020개, 요소수 512개)은 선형 탄성 재료로 모델링하였으며, PUF(노드수 6,545개, 요소수 5,760개)의 경우 본 고에서 선정한 재료 모델의 타당성을 확인하기 위해 밀도가 130kg/m3인 FU_CHANG_FOAM 모델 외에 직교 이방성 탄성 재료를 추가로 검토하였다. 낙하체와 Plywood 상면과의 접촉부는 면 접촉 조건으로 구현하였으며, 해석시 시간 증분은 전 절에 기술한 재료 모델링시 사용한 방법과 동일하게 선정하였다.
4.2 시뮬레이션 결과 및 고찰
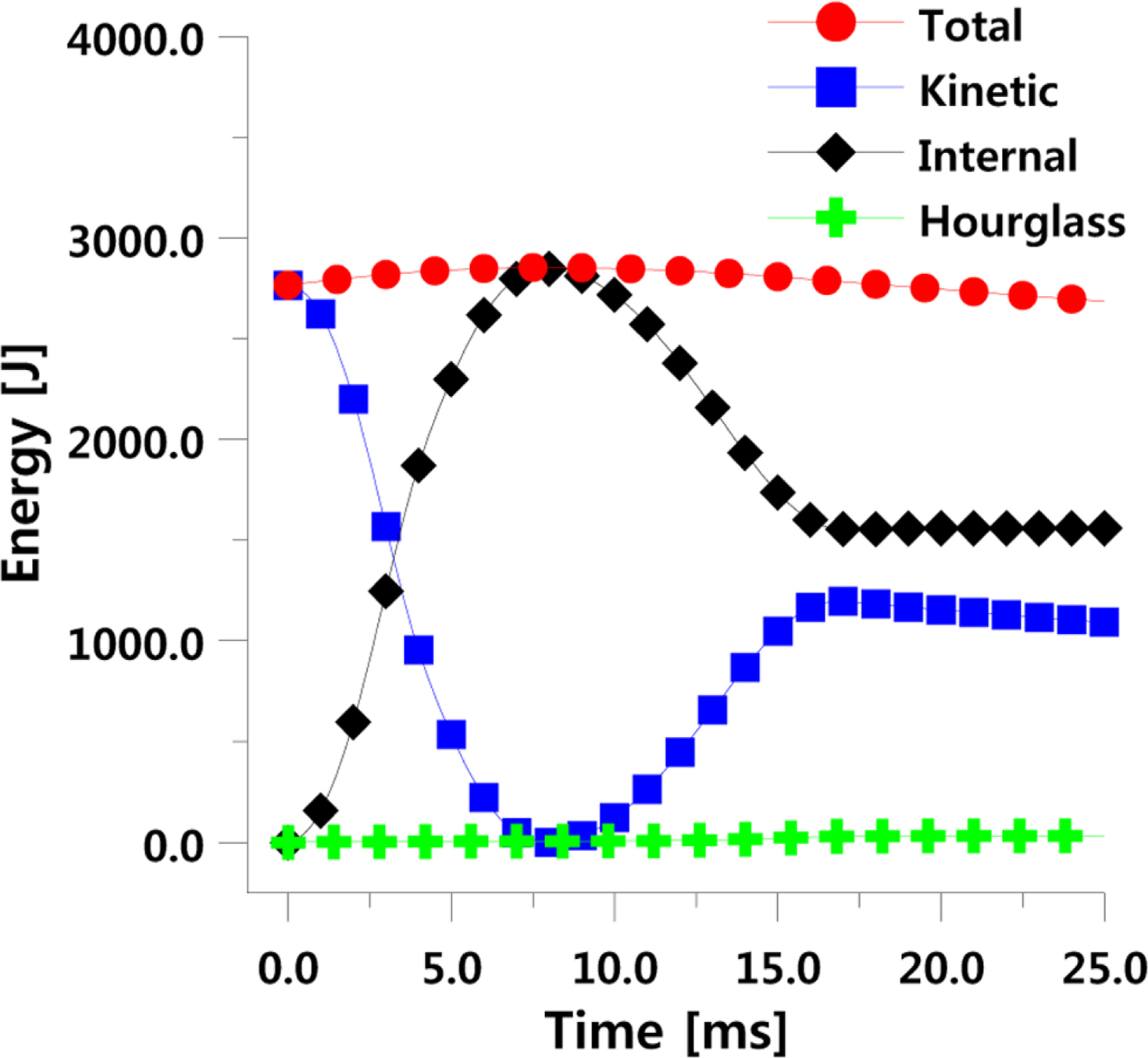
LS_DYNA 등과 같은 외연적 시간 적분법을 이용한 충돌 해석시 에너지 평형을 만족하는지 여부를 평가함으로써 해석이 적절히 수행되었는지 판단할 수 있다. 외연적 시간 적분을 이용한 해석시 총 에너지는 운동 에너지, 내부 에너지 그리고 Hourglass 에너지의 합으로 정의되는데, Hourglass 에너지는 외연적 시간 적분을 이용한 해석에서 해석 시간을 줄이기 위해 사용되는 감차 적분 요소에 의해 발생하는 해석 결과의 불안정성을 줄이기 위해 인위적으로 추가되는 에너지를 의미한다. 통상적으로 해석 결과의 적절성을 담보하기 위해서는 충돌 및 충격 하중이 가해지는 동안 Hourglass 에너지는 전체 에너지의 10% 이하가 되어야 하며 전체 에너지는 일정하게 유지되어야 하는 것으로 알려져 있다(Gama and Gillespie, 2011). Fig. 12는 낙하 높이가 415mm일 때의 Dry drop 해석 결과로부터 얻은 전체 에너지와 운동에너지, 내부 에너지 그리고 Hourglass 에너지의 변화를 도시한 것이다. Fig. 12와 같이 전 해석 기간 동안 전체 에너지는 680kg의 낙하체가 415mm의 위치에서 가지는 위치 에너지인 약 2,800J을 유지하고 있으며, Hourglass 에너지 또한 거의 ‘0’ 수준임을 알 수 있다. 이는 외연적 시간 적분법을 이용한 본 연구의 Dry drop 시뮬레이션이 적절히 수행되었음을 의미하는 결과이다.
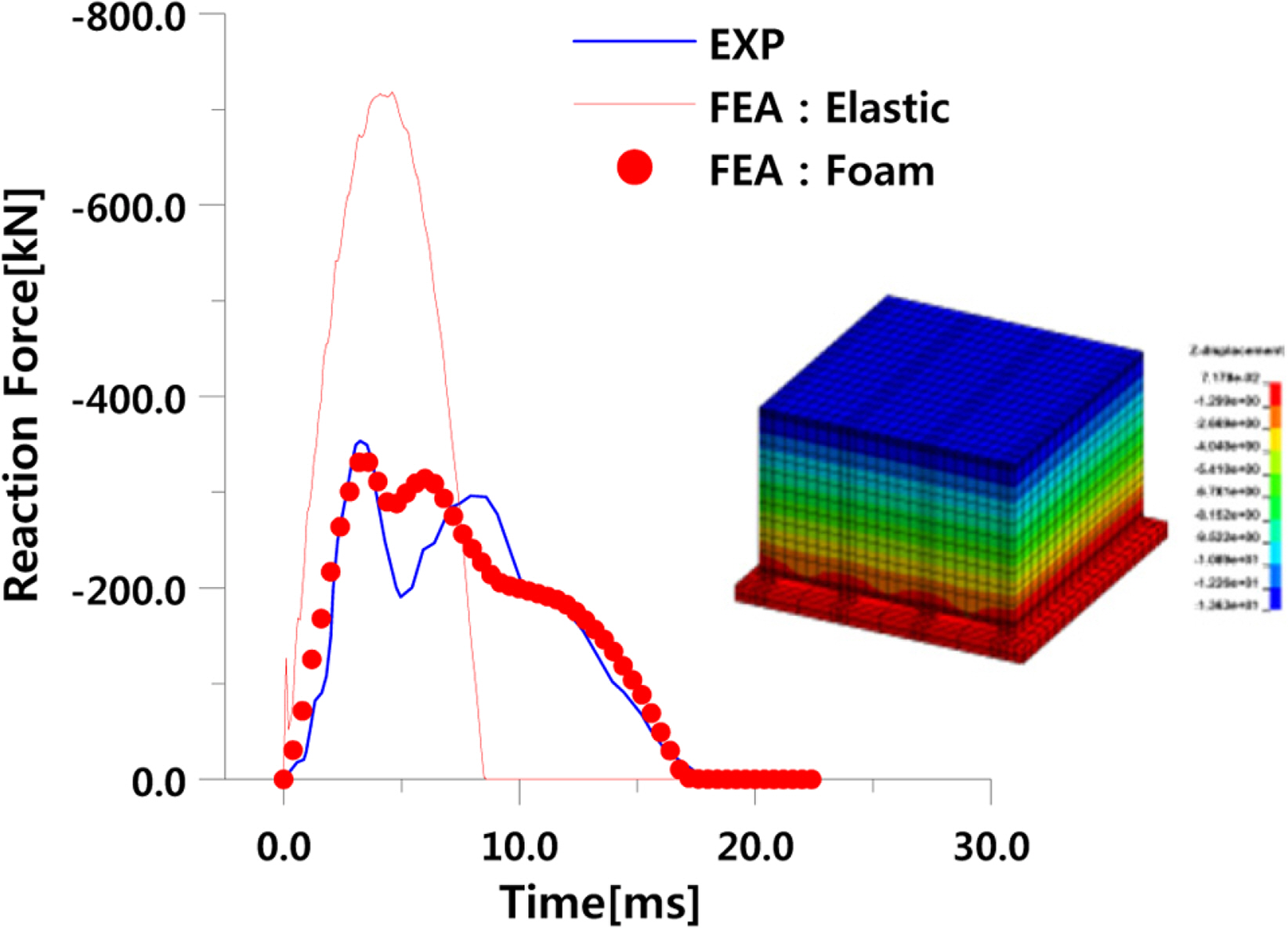
Fig. 13은 낙하 높이가 415mm인 경우 PUF의 재료 모델에 따른 유한요소해석과 실험을 통해 얻은 시간에 따른 반력을 비교한 결과이다. Fig. 13과 같이 PUF의 재료 모델로 FU_CHANG_ FOAM 모델을 적용한 경우 유한요소 해석 결과가 시험체에 작용하는 반력을 최대 오차률이 2% 미만으로 잘 예측하고 있을 뿐만 아니라 충격 지속 시간 또한 정확하게 일치하는 결과를 보인다. 반면 PUF 재료 모델로 직교 이방성 탄성 재료를 사용한 경우 시험체에 작용하는 반력은 유한요소해석 결과가 시험 대비 2배 이상 크며 충격 지속 시간은 시험 대비 1/2 수준으로 큰 차이가 있음을 알 수 있다. 이는 대표적인 에너지 흡수재인 PUF의 동적 특성을 FU_CHANG_FOAM 모델이 잘 모사하고 있음을 의미하는 결과이다. 이상의 결과로부터 본 연구에서 선정한 PUF의 재료 모델이 동적 충격 하중에 노출된 멤브레인형 LNG CCS의 동적 거동을 평가하는 데 적절함을 알 수 있다.
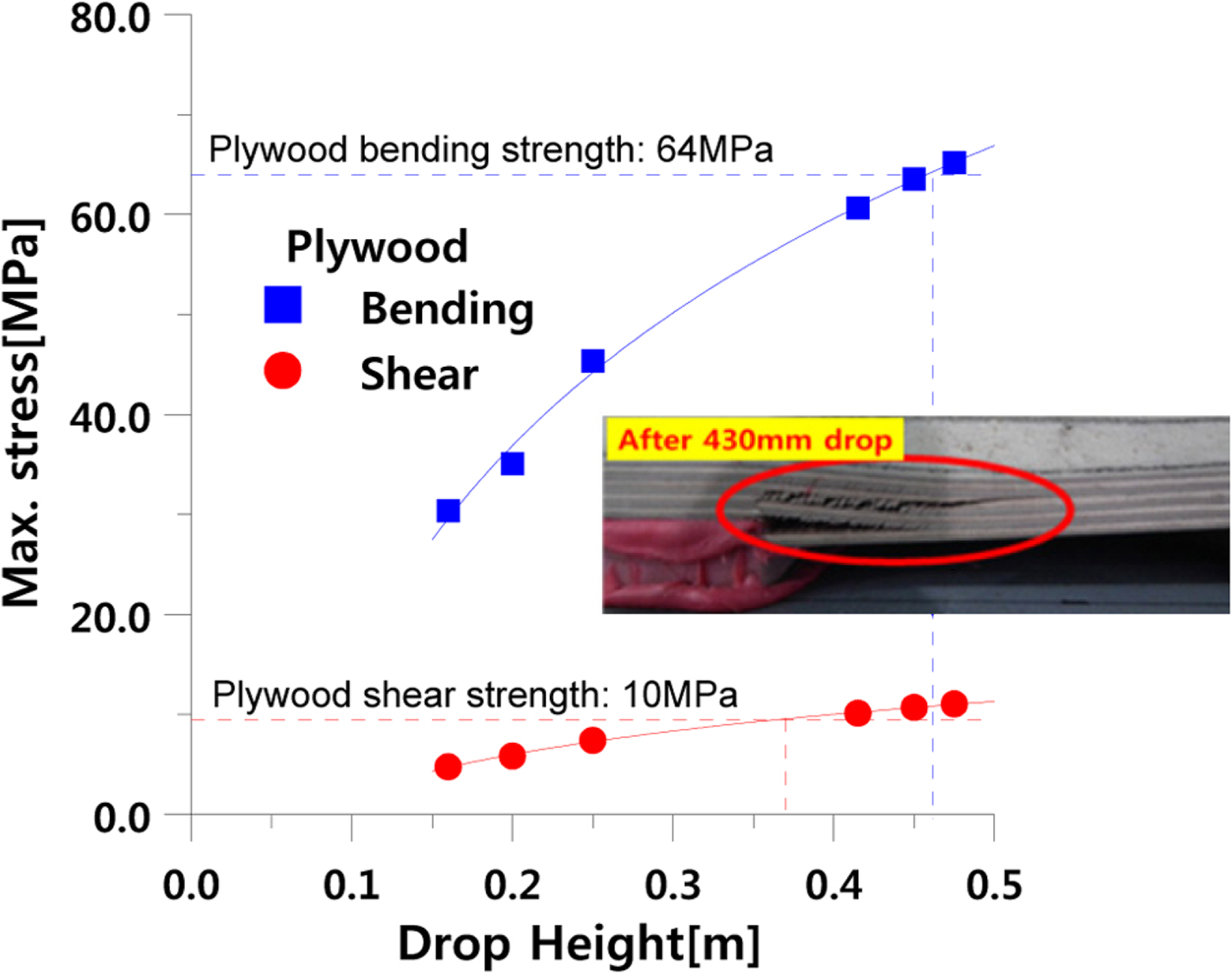
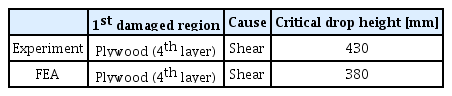
PUF의 동적 거동을 모사하기 위한 FU_CHANG_FOAM 모델을 이용하여 충격 하중하에서 시험체의 동적 강도를 평가하기 위해 다양한 낙하 높이를 변수로 Dry drop 시뮬레이션을 수행하였다. 이 때 시험체의 재료 모델은 전 절에서 기술한 바와 같이 Plywood는 직교이방성 탄성 모델을 사용하였으며 마스틱은 등방성 탄성 모델을 사용하였다. Fig. 14는 Table 6의 적층 구조를 가지는 시험체의 낙하 높이에 따른 Dry drop 시험시 가장 먼저 파단이 발생한 Plywood에서의 최대 응력 변화를 낙하 높이에 따라 도시한 것이다. 이 때, 응력은 충격 하중 작용시 시험체가 상대적으로 취약할 것으로 판단되는 마스틱과 Plywood 접합 단부에서의 전단 응력과 마스틱 로프(Rope) 사이에 발행하는 굽힘 응력으로 선정하였다. Fig. 14와 같이 낙하 높이가 증가함에 따라 직교 탄성 모델을 사용한 Plywood에 작용하는 응력이 선형적으로 증가함을 알 수 있다. 참고로, Dry drop 시험 결과 Plywood는 최초로 430mm의 높이에서 면외 방향 전단에 의해 발생하였다. Fig. 14의 결과로부터 시험체가 최초로 파손되는 순간의 높이로 정의되는 임계 낙하 높이를 평가하고 이를 Table 8에 나타내었다. 임계 낙하 높이를 결정하기 위한 Plywood의 면외 전단 강도와 굽힘 강도는 참고 문헌으로 부터 각각 10MPa (Latvijas, 2017)와 64MPa(Kim et al., 2017)로 선정하였다. Table 8와 같이 시험 결과와 유한요소해석 결과 모두 첫 번째 파손은 Plywood에서 발생하였으며, 파손 원인은 마스틱과 Plywood 접착 단부에서의 면외 방향 전단 응력이다. Dry dorp 시뮬레이션을 통해 평가된 임계 낙하 높이는 380mm로 시험에 의해 평가된 430mm에 비해 약 10% 작게 평가되었다. 그러나, 시험의 경우 육안으로 판별이 가능한 파손 시점을 임계 낙하 높이로 선정한 데 비하여 유한요소해석에서는 국부적인 응력을 기준으로 임계 낙하 높이가 평가되었다는 점을 감안한다면 유한요소해석이 시험 결과를 비교적 잘 예측하고 있으며, Plywood의 동적 강도 특성이 반영된다면 보다 정확한 평가가 가능할 것으로 생각된다. 이상의 결과로부터 본 연구에서 제안한 PUF의 동적 거동을 모사하기 위한 재료 모델링 기법은 향후 충격 하중 조건에서 멤브레인형 LNG CCS의 동적 응답 특성과 동적 강도 평가에 활용 가능함을 알 수 있었다.
5. 결 론
본 연구는 다양한 밀도를 가지는 PUF를 대상으로 온도와 변형률 속도에 따른 정⋅동적 재료 시험 결과와 유한요소해석을 활용하여 극저온 환경에서 충격 하중을 받는 멤브레인형 LNG CCS의 동적 거동 평가에 활용 가능한 PUF 재료 모델링 기법을 제안하고 다음과 같은 결론을 얻었다.
(1) 유리 섬유 강화 PUF의 동적 거동을 모사할 수 있는 재료 모델 개발을 위하여 준정적 압축 시험과 저속 충격 시험을 수행하여 상온과 극저온에서 밀도 및 변형률 속도에 따른 PUF의 거동을 특성화할 수 있는 기계적 물성을 확보하였다.
(2) 재료 시험 결과 모든 조건에서 본 연구에서 대상으로한 멤브레인형 LNG CCS용 PUF는 전형적인 폼 재료가 가지는 점탄소성 거동을 보이며 극저온 충격 조건에서 폼 발포 방향으로 채취된 시편이 발포 수직 방향으로 채취된 시편보다 안정적인 압축 변형 거동을 보임을 알 수 있었다.
(3) 재료 시험 결과를 수치적으로 모사하기 위해 선정한 LS_DYNA의 FU_CHANG_FOAM 모델이 PUF의 동적 거동을 정확하게 예측할 수 있어 FU_CHANG_FOAM 모델이 충격 하중하에서 PUF의 점탄소성 거동을 모사하는데 적합함을 알 수 있었다.
(4) 개발된 PUF의 재료 모델을 검증하기 위해 Dry drop 시험을 수치적으로 시뮬레이션하고 그 결과를 시험과 비교한 결과, 제안된 PUF의 재료 모델을 이용한 수치 해석 결과가 실험으로 계측된 시간에 따라는 반력, 변형 거동 등과 같은 동적 응답 특성과 시험체의 파괴 거동을 잘 예측하였다.
(5) 결론적으로 극저온 환경에서 변형률 속도에 의존하는 PUF의 동적 거동을 수치적으로 모사할 수 있는 재료 모델링 기법을 성공적으로 제안함으로써 향후 유한요소해석을 통해 충격 하중하에서 멤브레인형 LNG CCS의 동적 응답과 강도 평가에 활용 가능한 기반 기술을 확보하였다.