Study on Moonpool Resonance Effect on Motion of Modern Compact Drillship
Article information
Abstract
A drillship is a representative floating offshore installation. The boom in oil and gas field development has dramatically increased the demands for drillships. Drillships have a moonpool in the center area of the ship for the purpose of drilling. This moonpool has an effect on the seakeeping performance of a drillship in the vicinity of the resonance frequency. Because of the moonpool, drillships act in different resonance modes, called the sloshing mode and piston mode. The objective of this study was to find the moonpool effect on the motion of a drillship through the motion analysis of a currently operating modern compact drillship. The predicted resonance frequencies based on Molin's theoretical formula, Fukuda's empirical formula, and BEM-based numerical analysis are compared. The accuracy of the predictions using the theoretical and empirical formulas is compared with the numerical analysis and evaluated. In the case of the piston mode, the difference between the resonance frequency from theoretical formula and the resonance frequency from the numerical analysis is analyzed. The resonance frequency formula for more a complex moonpool geometry such as a moonpool with a cofferdam is necessarily emphasized.
1. Introduction
Drillships have a self-propulsion system which functions very similar with the propulsion system of commercial ships. The self-propulsion system enables a drillship to move from one oil field to another. Drillships have additional systems for drilling which includes a large cavity called a 'moonpool' in the centre area of the ship. Moonpools are constructed in different shapes including circles, squares, rectangles and so on. Among the different shapes of moonpools, rectangular shaped moonpools with and without a cofferdam are common in recently constructed compact drillship.
According to previous studies, the moonpool has an effect on the seakeeping performance of the drillship in the vicinity of resonance frequency. The drillship acts in two different resonance modes called the sloshing mode and the piston mode. The effects of moonpool resonance can be summarized as follows: the change of the drillship motion in the vicinity of resonance frequency and flow inside a moonpool caused by moonpool resonance. While a drillship is in transit, the main concern is added resistance caused by the moonpool.
There have been many studies to predict moonpool resonance and the reduction of flow inside the moonpool. The work by Fukuda on model test are referred as one of the outstanding researches. Fukuda carried out empirical research on the behavior of ship-shaped floating offshore installations (Fukuda, 1977). He observed the flow inside the moonpool using models with circular and square shaped moonpools and studied the effect caused by the violent flow inside the moonpool on vessel motion. Throughout the analysis of model test results, the phenomena of the sloshing mode and the piston mode were described and it was found that they are closely related to the shape of the moonpool and the flow velocity around the vessel.
Recently, Molin conducted theoretical moonpool related research. Molin (2001) has derived theoretical formulas for resonance frequencies of a moonpool in the sloshing mode and the piston mode using velocity potential and boundary condition. He applied those formulas to a barge with a moonpool.
Maisondieu and Ferrant (2003) obtained moonpool resonance frequency from Fast Fourier Transform of time histories of free surface elevation inside a moonpool and it was compared with predicted resonance frequency from theoretical formula.
Gaillarde and Cotteleer (2004) developed several methods and devices to reduce the flow inside a moonpool and confirmed the effect of each device on forward speed.
Veer and Tholen (2008) performed resistance tests on moonpools with various ratios of length to breadth. They studied the correlation between the shape of the moonpool and increase of resistance, and the variation of free surface elevation inside the moonpool according to the ratio of draft to moonpool breadth. On the basis of this study, the prediction model for increase of resistance, called "the 'piston' added resistance prediction model", was suggested.
Park (2009) carried out model tests in 2D wave flume to find the variation of flow inside a moonpool along with a change of breadth of a moonpool and devices for flow reduction and analyzed model test results. Taylor et al. (2009) investigated the viscous effect on the prediction of violent flow inside a moonpool and the difference between potential based prediction results of free surface elevation inside a moonpool and the model test results.
Choi et al. (2010) performed flow analysis for different shaped moonpools using an in-house computational fluid dynamics (CFD) code to investigate the complex mechanism of violent flow inside a moonpool. This study used a model with a cofferdam. The overturn of free surface due to the existence of the cofferdam and the forming process of the complex flow field were examined. On the basis of this study, the optimized shape of a moonpool was suggested after a review of the characteristics of flow inside the moonpool and the added resistance for the different shapes of moonpools. Choi et al. (2011) and Heo et al. (2011) carried out 2D CFD simulations for the forced heave oscillation of a 2D floating body with a moonpool and compared it with the variation of free surface elevation for Faltinsen's 2D model test result. From this study, it was confirmed that the analysis considering viscosity is closely aligned with the model test results. He found that the flow field inside the moonpool could be affected by the generation of a vortex.
Most recently, MARIN (Maritime research institute netherlands) has been studying the moonpool resonance mechanism through model tests in its basin in the "Moonpool Joint Industry Project" organized by MARIN (Kooiker, 2011).
According to previous studies, flow inside a moonpool is very violent in the resonance condition and depends on the size and shape of the moonpool, as well as the draft, and transit speed. In this study, the change of drillhsip seakeeping performance due to the effect of moonpool resonance will be described. In addition, the predicted resonance frequencies based on Molin's theoretical formula, Fukuda's empirical formula and BEM (Boundary element method) based numerical analysis are compared. The accuracy of predictions using theoretical and empirical formula is compared and evaluated. Throughout the motion analysis of a currently operating modern compact drillship, the moonpool resonance effect on the drillship motion will be investigated extensively.
2. Numerical Method
2.1 Ship motion analysis program: PRECAL (Pressure calculation program for 3D seakeeping problems)
For motion analysis of the drillship, PRECAL (Ver.6.5) was used. PRECAL is a 3-dimensional linear ship motion code based on potential theory. The theoretical background of the PRECAL program is in the "PRECAL theory manual" (MARIN, 2009) and the modules and function of each module are as follows:
Main program consists of 4 modules.
- HYDMES: generation of hull surface panel including undisturbed free surface and calculation of static load.
- HYDCAL: calculation of potential components including velocity potential, source strength for hydrodynamic force using Green function.
- RESCAL: motion response and calculation of wave load in regular and irregular wave.
- FINMES: post-processing module for pressure calculation in the centre of hydrodynamic mesh.
2.2 Coordinate System
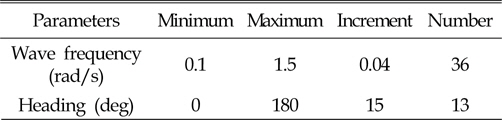
Wave direction and the definition of ship motion are shown in Fig. 1. Wave frequency and heading angle used in the analysis are shown in Table 1
2.3 Models and Conditions of Analysis
In this study, a currently operating drillship was selected as a target vessel for practical application, and the vessel motion analysis of operation conditions were performed. Moonpool dimensions are shown in Table 2. L and B represent vessel length and vessel breadth.
Drillship panel models for the analysis are shown in Fig. 2. To investigate the moonpool effect on drillship motion, analyses of models with and without a moonpool were performed. In the case of the model with a moonpool, analyses of models without a cofferdam and with a cofferdam were carried out. To generate vertical walls and a cofferdam inside the moonpool, Patran was used as a panel modeling tool.
The draft for the model is 11 meters. Operating condition was selected for the practical usefulness.
3. Theory of moonpool resonance: Piston mode and Sloshing mode
3.1 3-dimensional moonpool resonance of piston mode and sloshing mode
In the case of a 3-dimensional moonpool, the resonance frequencies of the piston mode and the sloshing mode due to the effect of a moonpool can be obtained through the following procedure. By assuming equation (1) in heave motion equation, the resonance frequency of this system represents piston mode resonance frequency of the moonpool.


where, m is mass of moonpool, m′ is added mass, c is spring constant respectively.
Since the spring constant and the mass of a moonpool can be obtained by using moonpool length, moonpool breadth, and draft, the resonance frequency of the piston mode can be expressed in (2).
In the case of a 3-dimensional moonpool, the resonance frequencies of the piston mode and the sloshing mode due to the effect of the moonpool can be obtained by the followings.

where, d is draft and d′ is added draft.
Fukuda (1977) expressed added draft as the following empirical formula.

where, S is plane area of moonpool.
Molin (2001) expressed the resonance frequency of piston mode using velocity potential as (5).

where, h =draft, b=moonpool breadth, C = 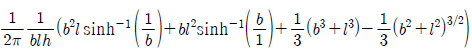
Meanwhile, n-order resonance frequency of sloshing mode is suggested by Newman (1977) as shown in (6).

where, n is order of resonance, l is moonpool length.
Molin (2001) suggested the following formula for the resonance frequency of the sloshing mode including the draft of a moonpool through the derivation of velocity potential.

where, 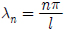
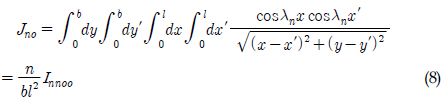
Equation (8) can be presented as the following simple integral form.
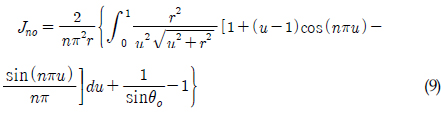
where,  , and tanθo = r- 1
, and tanθo = r- 1
4. Numerical calculations and analysis results
4.1 Motion response and moonpool resonance
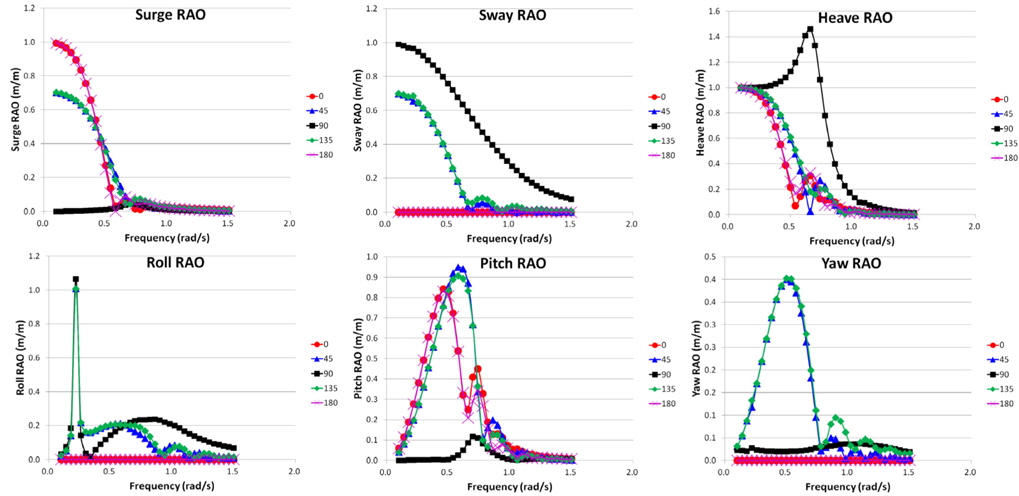
The cases analyzed are as follows: the model with a moonpool and the model without a moonpool. For the latter case, the model with a cofferdam and the model without a cofferdam were considered. The analysis results are summarized in the RAO (Response amplitude operator) forms of motion responses of the drillship as shown in Fig. 3 ~ Fig. 5.
In the case of the model without a moonpool, the form of generally witnessed RAOs for commercial ships is obtained. In the case of the model with a moonpool, the peaks appeared in surge RAO and heave RAO respectively. This represents the phenomenon due to the moonpool and the purpose of this studyis the analysis of it.
4.2 Moonpool resonance
The predictions of resonance frequencies based on Molin's theoretical formula (2001) of a 3-dimensional moonpool reso nance frequencies of the piston mode and the sloshing mode are summarized in Table 3 and Table 4.
Table 5 presents the predicted multiple resonance frequencies of the four lowest sloshing modes based on Molin's theoretical formula.
In the case of the vessel with a moonpool, it is known that the resonance phenomenon of a moonpool appears according to the size of a moonpool, the shape of a moonpool, draft, and vessel speed.
From an operational point of view, it is important to find the resonance frequency of a moonpool. Wave conditions with resonance of a moonpool and violent flow inside a moonpool in the vicinity of resonance frequency need to be evaluated in advance to ensure the safety of workers and to protect the drilling equipments. For the target vessel, the sloshing mode resonance and the piston mode resonance appeared in the analysis results.
In the sloshing mode, the resonance frequencies of 1.02 rad/s and 0.86 rad/s for the models with and without a cofferdam appeared respectively. In the piston mode, the resonance frequencies of 0.78 rad/s and 0.54 rad/s for the models with and without a cofferdam appeared respectively. Comparing the results from motion analysis with the predicted resonance frequency from the theoretical formula of the sloshing mode, the comparison shows good agreement irrespective of a cofferdam. For the model without a cofferdam, the resonance frequency from numerical analysis is a little (0.08 rad/s) higher than the theoretical formula. The model with a cofferdam is slightly lower (0.08 rad/s) than the theoretical formula. The comparison between the model without a cofferdam and the model with a cofferdam shows that the latter is 0.16 rad/s lower than the former.
However, in the piston mode, the resonance frequency of the model without a cofferdam and that from the theoretical formula shows reasonably good agreement. For the case of the model with a cofferdam, the resonance frequency is 0.15 rad/s lower than that from the theoretical formula. This may be due to the following reasons. First, the theoretical formula assumed a barge shaped motionless vessel, and regarded the vessel as an infinite beam. Second, the formula derived from a square moonpool has a limitation for predicting the resonance frequency since the target drillship has complex geometry with a cofferdam inside the moonpool (Fig. 7) compared with the model without a cofferdam (Fig. 6). Physically, it is presumed that the resonance frequency of a moonpool shifted to the different frequency since flow inside a moonpool is restrained due to the effect of the cofferdam and flow becomes complicated.
At the same time, it is known that the resonance frequency of the piston mode is lower than the sloshing mode. The resonance frequency of the sloshing mode is around 1.5 time higher than the resonance frequency of the piston mode. This is shown in Table 6.
4.3 Effect of vessel speed on moonpool resonance
Most of the previous studies did not consider the effect of vessel speed on the prediction of the resonance frequency of a moonpool. In particular, Molin's theoretical formula assumed a motionless vessel. Therefore, the prediction of resonance frequency of a moonpool considering vessel speed is required. In this study, numerical calculations of moonpool resonance were performed in the case of zero speed of a drillship as well as cases with forward speed.
The objective in investigating into forward speed is to find out the moonpool effect on drillship motion during transit. For the purpose of simplicity, the model with a square moonpool is selected as analysis case. Speed ranges are 0 knots in operating condition to 12 knots in design transit speed.
The analysis results are summarized as follows:
- Due to the effect of speed, different resonance frequencies of the moonpool are appeared according to wave direction.
- The sloshing mode and the piston mode resonance frequencies moves to higher or lower frequency according to the incoming wave direction.
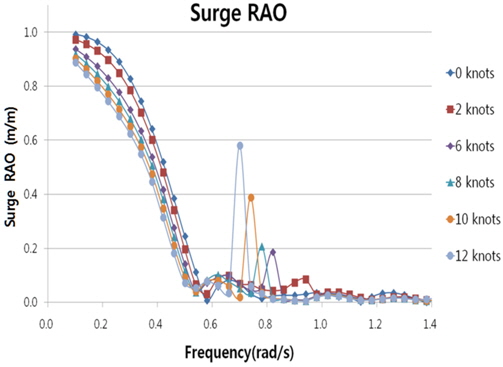
- For head sea condition, the analysis results show an almost linear relation between speed and resonance frequency as shown in Fig. 8
- Not only locations of resonance frequencies in RAOs but also amplitudes of RAOs in resonance frequencies are different for forward speed cases as shown in Fig. 9. This means that the effect of speed to the motion is very complex and varies with the speed of the drillship
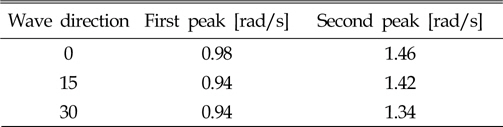
- 0 degree, 15 degree, 30 degree at 4knots in the piston mode presents two peaks. This can be explained as the examples or possibilities of multiple mode resonances as shown in Table 7 and Fig. 10. However, further studies are required to explain these characteristics in moonpool resonance frequencies for forward speed case.
5. Conclusions and Future Work
In this study, the moonpool effect to the motion of a drillship was investigated extensively.
Due to the existence of a moonpool, drillships have two different resonance modes, the sloshing mode and the piston mode, and the moonpool has an effect on the seakeeping performance of the drillship in the vicinity of resonance frequency.
From an operational point of view, the prediction of resonance frequency is very important. In this study, the predictions of resonance frequencies from Molin's theoretical formula and Fukuda's empirical formula are compared and evaluated by numerical analysis result. The following conclusions are drawn from this study on the prediction of resonance frequency of a moonpool.
In the sloshing mode, the model without a cofferdam shows good agreement with Newman's theoretical formula, Molin's theoretical formula, and numerical results. However, in the case of the model with a cofferdam, the resonance frequencies based on theoretical formula and numerical result are slightly different.
In the piston mode, in the case of the model without a cofferdam, Molin's theoretical formula, Fukuda's empirical formula, and numerical analysis show comparable agreement. In the case of the model with a cofferdam, the numerical analysis result is a little lower than those of Molin's theoretical formula and Fukuda's empirical formula. It may be that the effect of a cofferdam and the formula derived from a square moonpool has a limitation for prediction of the resonance frequency for the model with a complex moonpool geometry such as the model with a cofferdam.
For future work, the formula for the prediction of resonance frequency of more complex moonpool geometry in the case of model with a cofferdam is required. In addition, the formula for the prediction of resonance frequency for drillships with transit speed is required for initial design purpose.
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MEST) (No. 2011-0030670)
References
Choi, S.Y., Lee, Y.G., Jung, K.Y., 2010. A Fundamental Study for Internal Flow in Moonpool Using Marker-Density Method by Two-Dimensional Numerical Simulation. Spring Conference of the Society of Naval Architects of Korea, Jeju.
Choi S.Y., Lee Y.G., Jung K.Y.. A Fundamental Study for Internal Flow in Moonpool Using Marker-Density Method by Two-Dimensional Numerical Simulation In : Spring Conference of the Society of Naval Architects of Korea. Jeju; 2010.Choi, S.Y., Lee, Y.G., Jung, K.Y., Ha, Y.G., 2011. Reduction of Added Resistance by Internal Flow Control in the Moonpool of a Drillship. Journal of the Society of Naval Architects of Korea, 48, 544-551.
Choi S.Y., Lee Y.G., Jung K.Y., Ha Y.G.. Reduction of Added Resistance by Internal Flow Control in the Moonpool of a Drillship. Journal of the Society of Naval Architects of Korea 2011;48:544–551. 10.3744/SNAK.2011.48.6.544.Fukuda, K., 1977. Behavior of Water in Vertical Well with Bottom Opening of Ship and its Effects Ship-Motion. Journal of the Society of Naval Architects of Japan, 141, 107- 122.
Fukuda K.. Behavior of Water in Vertical Well with Bottom Opening of Ship and its Effects Ship-Motion. Journal of the Society of Naval Architects of Japan 1977;141:107–122.Gaillarde, G., Cotteleer, A., 2004. Water Motion in Moonpools Empirical and Theoretical Approach, ATMA.
Gaillarde G., Cotteleer A.. Water Motion in Moonpools Empirical and Theoretical Approach ATMA; 2004.Heo, J.K., Park, J.C., Kim, M.H., 2011. CFD Analysis of Two- Dimensional Floating Body with Moonpool under Forced Heave Motion. Journal of Ocean Engineering and Technology, 25(2), 36-46.
Heo J.K., Park J.C., Kim M.H.. CFD Analysis of Two- Dimensional Floating Body with Moonpool under Forced Heave Motion. Journal of Ocean Engineering and Technology 2011;25(2):36–46.Kooiker, K., 2011. Moonpool Mysteries. MARIN Report, 104, 18.
Kooiker K.. Moonpool Mysteries. MARIN Report, 104 2011. 18.Maisondieu, C., Ferrant, P., 2003. Evaluation of the 3D Flow dynamics in a Moonpool. Proceedings of the Thirteenth International Offshore and Polar Engineering Conference.
Maisondieu C., Ferrant P.. Evaluation of the 3D Flow dynamics in a Moonpool In : Proceedings of the Thirteenth International Offshore and Polar Engineering Conference; 2003.Maritime Research Institute Netherlands (MARIN), 2009. PRECAL V6.5 Theory Manual. MARIN Report, 17926-2-CPS, 2009
. PRECAL V6.5 Theory Manual 2009.Molin, B., 2001. On the Piston and Sloshing Modes in Moonpools. Journal of Fluid Mechanics, 430, 27-50.
Molin B.. On the Piston and Sloshing Modes in Moonpools. Journal of Fluid Mechanics 2001;430:27–50. 10.1017/S0022112000002871.Newman, N., 1977. Marin Hydrodynamics. The MIT Press, Cambridge.
Newman N.. Marin Hydrodynamics The MIT Press. Cambridge: 1977.Park, S.J., 2009. Hydrodynamic Characteristics of Moonpool shapes. MSc Thesis PNU.
Park S.J.. Hydrodynamic Characteristics of Moonpool shapes. MSc Thesis PNU; 2009.Taylor, R.E., Sung, L., Taylor, P.H., 2009. Gap Resonances in Focused Wave Groups. Proceedings of the 23rd International Workshop on Water Waves and Floating Bodies.
Taylor R.E., Sung L., Taylor P.H.. Gap Resonances in Focused Wave Groups In : Proceedings of the 23rd International Workshop on Water Waves and Floating Bodies; 2009.Veer, R., Tholen, H.J., 2008. Added Resistance of Moonpools in Calm Water. Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering.
Veer R., Tholen H.J.. Added Resistance of Moonpools in Calm Water In : Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering; 2008.