AQWA User's Manual Version 13 ANSYS Inc.; Southpointe, USA: 2010.
Bela, H.B., Cornelia, M.B.. (The Offshore-ring: A New System Design for the Open Ocean Aquaculture of Macroalgae Institute for Polar and Marine Research, Helgoland, Germany: 2004.
Cummins, W.E.. (The Impulse Response Function and Ship Motions ISST, Hamburg, Germany: 1962.
Fredriksson, D.W., Swift, M.R., Eroshkin, O., Tsukrov, I., Irish, J.D., Celikkol, B.. (Moored Fish Cage Dynamics in Waves and Currents, IEEE Journal of Oceanic Engineering, 2005). 30(1):28-36 10.1109/JOE.2004.841412.

Goda, Y.. (Random Seas and the Design of Maritime Structures World Scientific Publishing Company, New Jersey: 2000.
Jord├Īn, M.A., Beltr├Īn-Aguedo, R.. (Nonlinear Identification of Mooring Lines in Dynamic Operation of Floating Structures, Ocean Engineering, 2004). 31, 455-482 10.1016/S0029-8018(03)00122-7.

Journee, J.M.J., Massie, W.W.. (Offshore Hydromechanics First Edition Delft University of Technology, 2001.
Kim, J.H., Kim, H.J., Hong, S.. (Experiment and Analysis of Mooring System for Floating Fish Cage, Korean Journal of Fisheries and Aquatic Sciences, 2001). 34(6):661-665.
Kim, J, H., Hong, S.Y., Hong., S.W, Hong, S.. (An Experimental Study on Compliant Buoy Mooring System in Shallow Water Proceeding of 2002 Spring Conference Korean Society for Ocean Engineers 2002). 155-160.
Korea-India Joint Research for Ocean Renewable Energy Development Korea Institute of Ocean Sciences and Technology, 2003.
Deep Water Design Wave Prediction II Korea Institute of Ocean Sciences and Technology, 2005.
Strategies to Industrialize the Algae Bio-business and Policy Direction Korea Maritime Institute, 2009.
Lien, E., Oltedal, G., Aarsnes, J.V.. (Application of Computer Simulation Program in Design of Fish Farming Plants Norwegian Marine Technology Research Institute, Trondheim, Norway: 1989.
Lien, E., Oltedal, G., Aarsnes, J.V.. (Flexible Mooring with Multiple Buoys Open Ocean Aquaculture Conference Polk, M Ltd.; Portland: 1996). 93-105.
Nam, B.W., Kim, Y., Yang, K.K., Hong, S.Y., Sung, H.G.. (Numerical Study on Wave-induced Motion of Offshore Structures using Cartesian-grid based Flow Simulation Method, Journal of Ocean Engineering and Technology, 2012). 26(6):7-13 10.5574/KSOE.2012.26.6.007.


Newman, J.N.. (Marine Hydrodynamics The MIT Press, Cambridge, MA, USA: 1997.
Shin, S.H., Hong, K.. (Experimental Study on Wave Overtopping Rate of Wave Overtopping Control Structure for Wave Energy Conversion, Journal of Ocean Engineering and Technology, 2005). 19(6):8-15.
ANSYS AQWA Training (Basic course) Taesung SNE, 2011.
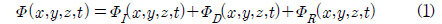
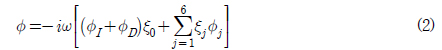
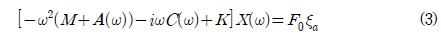
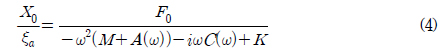
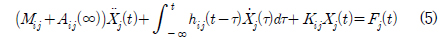
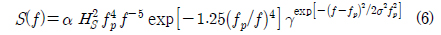
 ,
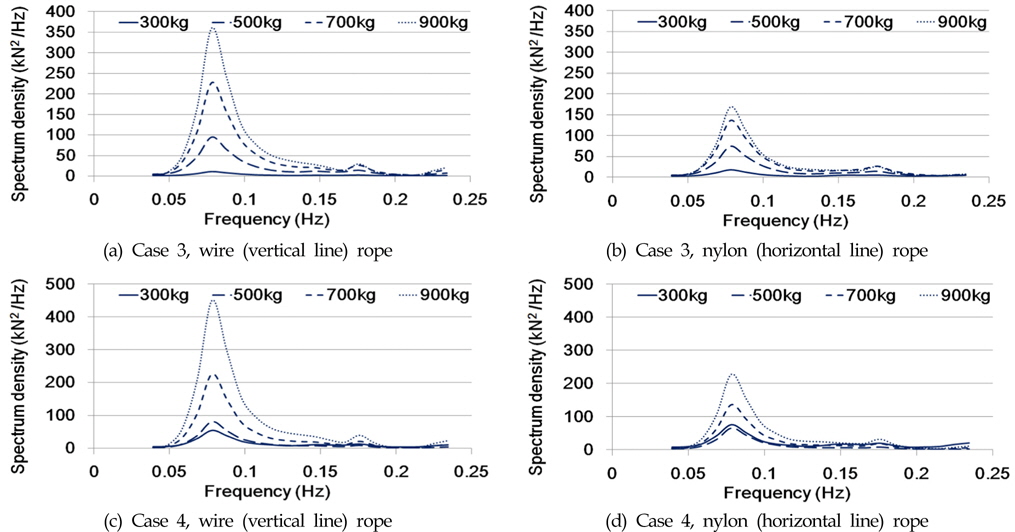
, 





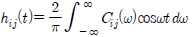 (ņ×äĒÄäņŖżņØæļŗĄĒĢ©ņłś),
(ņ×äĒÄäņŖżņØæļŗĄĒĢ©ņłś),