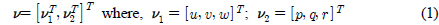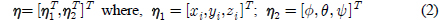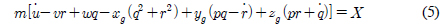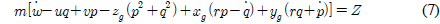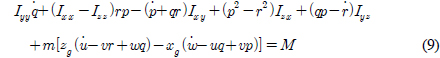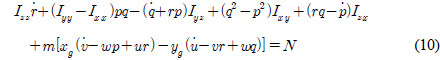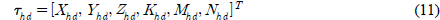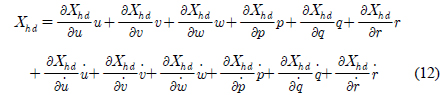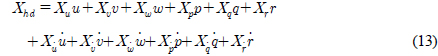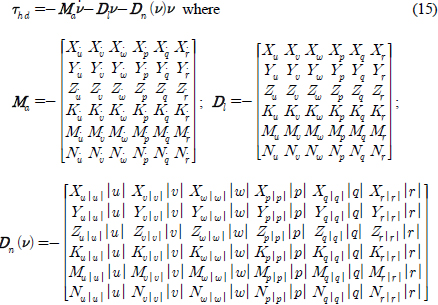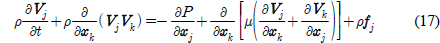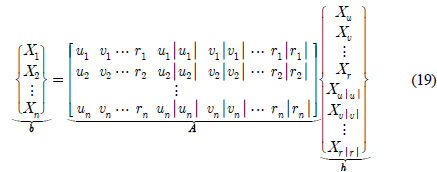|
 |
- Search
| J. Ocean Eng. Technol. > Volume 31(5); 2017 > Article |
|
Abstract
This paper introduces a simulation-based determination method for hydrodynamic derivatives and 6DOF (degrees-of-freedom) motion analysis for an underwater vehicle. Hydrodynamic derivatives were derived from second-order modulus expansion and composed of the added mass, and linear and nonlinear damping coefficients. The added mass coefficients were analytically obtained using the potential theory. All of the linear and nonlinear damping coefficients were determined using CFD simulation, which were performed for various cases based on the actual operating condition. Then, the linear and nonlinear damping coefficients were determined by fitting the CFD results, which referred to 6DOF forces and moments acting on an underwater vehicle, with the least square method. To demonstrate the applicability of the current study, 6DOF simulations for three different scenarios (L-, U-, and S-turn) were carried out, and the results were validated on the basis of physical plausibility.
시뮬레이션을 통한 수중 운동체의 운동성능 평가 방법은 수중 로봇 혹은 수중 운동체에 대한 설계의 효율성 및 운용 안전성 향상에 매우 중요한 정보를 제공해줄 수 있다. 이러한 운동성능을 파악하기 위해서는 해당 수중 운동체에 대한 신뢰성 있는 비선형 6자유도 운동해석이 반드시 필요하다. 수중 운동체에 대한 6자유도 운동방정식은 Fossen(1994) 등에 의해 정립이 되어있기 때문에 6자유도 운동해석에서 가장 중요한 요소는 수중 운동체에 작용하는 외력을 여하히 신뢰성 있는 방법으로 모델링 할 수 있는가 하는 점이다.
수중 운동체의 외력은 일반적으로 정수력, 동유체력, 제어력, 환경하중으로 구분된다. 여기서 정수력은 수중 운동체의 자세에 대한 함수로 정의되어 있기 때문에 수중 운동체의 자세에 따라 자동적으로 결정된다. 또한, 제어력과 환경하중은 시뮬레이션 관점에서 보았을 때 입력 변수이기 때문에 수중 운동체의 6자유도 운동해석에서의 핵심은 동유체력을 모델링하는 것이다. 특히, 자체적인 동력인 아닌 케이블 등에 의해 예인되는 수중 예인체(Tow-fish)의 경우 제어력이 없기 때문에 거동 예측에 있어서 정확한 동유체력 모델링이 매우 중요한 관건이다.
모델링 된 동유체력의 경우 유체력 미계수(Hydrodynamic derivatives)에 의하여 정식화된다. 현재까지 수중 운동체의 유체력 미계수는 포텐셜 이론을 기반으로 한 이론적인 접근방법, 반경험적(Semi-empirical) 방법 그리고 PMM(Planar motion mechanism), RA(Rotating arm) 시험과 같은 수조시험을 통해 결정되어왔다. 이론적인 방법은 부가질량을 예측하는 데는 적합하지만, 점성의 영향을 포함하는 감쇠계수를 결정하는 데는 많은 한계를 가지고 있는 것으로 알려져 있다. 반경험적 방법은 복잡한 형상을 충분히 고려할 수 없다는 단점이 있다. 수조시험은 유체력 미계수를 결정하는데 가장 효과적인 방법으로 널리 적용되고 있으나, 수조시험은 많은 비용을 필요로 할 뿐만 아니라 시간이 오래 걸리기 때문에 경제적인 관점에서 매우 비효율적인 방법이다(Pan et al., 2012; Shadlaghani and Mansoorzadeh, 2016).
최근 CFD(Computational fluid dynamics)에 대한 연구가 활발히 진행됨에 따라 유체력 미계수 결정에 새로운 대안으로 CFD가 활용되고 있다. Tyagi and Sen(2006)은 AUV(Autonomous underwater vehicle)의 유체력 미계수를 CFD 계산으로 결정하였다. 여기서는 좌우동요(Sway)와 관련된 감쇠계수만을 간단한 시뮬레이션을 통해 예측하였지만, 그 결과를 반경험적 방법으로 얻은 결과와 비교하여 CFD로 유체력 미계수를 추정할 수 있음을 보여주었다. Zhang et al.(2010)은 PMM 시험과정을 CFD 시뮬레이션으로 구현하여 AUV의 유체력 미계수를 결정하였고, 여러 가지 조종시험에서 발생하는 AUV의 거동특성을 검증하여 결정된 계수들의 타당성을 증명하였다. Pan et al.(2012)와 Shadlaghani and Mansoorzadeh(2016)은 SUBOFF 잠수함 모델의 유체력 미계수를 CFD로 결정하였다. 전자의 경우 경사예인시험과 PMM 시험을 CFD 시뮬레이션으로 구현하였고, 결과를 실험결과와 비교하였다. 후자는 경사예인시험과 RA 시험을 정상상태에 대한 시뮬레이션으로 구현하여 유체력 미계수를 결정하였다. 국내에서는 CFD를 활용하여 Ahn and Jung(2012)에 의해 단순한 형상의 수중 운동체의 유체력 미계수를 결정한 사례가 있으며, Go et al.(2016a)에 의해 수중 예인체의 유체력 미계수를 결정한 사례가 있다. 회전속도와 관련된 감쇠계수는 Santhakumar et al.(2009)에 의해 형상변화에 따른 민감도가 낮은 것으로 제시된 바 있어, Go et al.(2016a)에서는 회전속도와 관련된 감쇠계수는 유사선형을 값을 차용하고 병진속도에 대한 감쇠계수만을 결정하였다. 이상의 연구들 중에서 CFD해석은 주로 수조실험을 보완하는 방법으로 사용되어오고 있으며, 전체 유체력 미계수 중 일부에 대한 결정에 사용되었을 뿐 동유체력 정식화에 필요한 모든 유체력 미계수를 결정한 사례는 존재하지 않는다.
최근 Go et al.(2016b)의 연구에서는 CFD시뮬레이션을 통하여 결정된 유체력 감쇠계수를 이용하여 실제 수중 예인체의 해상시험 데이터를 성공적으로 예측해 낼 수 있음을 보여 주었다. 이를 통해 CFD 시뮬레이션을 통한 유체력 감쇠계수 결정 방법론의 타당성이 간접적으로 제시되었다고 할 수 있다. 본 연구에서는 CFD 시뮬레이션을 통한 유체력 미계수 결정법에 대한 일련의 수치적인 방법론을 구체적으로 제시하고자 한다.유체력 미계수는 Second-order modulus 전개로 유도하였으며, 부가질량은 포텐셜 이론을 바탕으로 이론적으로 결정하였다(Son et al., 2006; Go et al., 2016a). 모든 감쇠계수는 CFD 시뮬레이션을 통해 결정하였으며, 그 과정은 다음과 같다. 먼저 수중 예인체의 실제 운용조건을 기준으로 다양한 해석 케이스를 설정하였다. 다음으로 설정된 해석 케이스에 대하여 CFD 시뮬레이션을 수행 하였고, 마지막으로 CFD 해석을 통해 얻은 수중 예인체에 작용하는 6자유도 힘과 모멘트를 동유체력 모델링 식으로 커브피팅하여 모든 감쇠계수를 결정하였다. 커브피팅에는 최소자승법(Least square method)이 활용되었다. 이와 같이 본 연구는 일체의 수조시험이나 공학자의 직관에 의존하지 않고 순수 CFD 시뮬레이션만을 통하여 모든 성분의 감쇠계수를 결정했다는 점에서 그 독창성이 있다고 할 수 있으며, 뿐만 아니라 실제운용조건을 기준으로 설정된 가상의 상황을 기반으로 CFD 해석조건을 설정하여 축소 모형시험 등에서 발생되는 상사법칙의 불만족 가능성을 배제하였기에 기존 연구들과 차별화 된다.
본 논문의 나머지 부분은 다음과 같이 구성된다. 먼저 2절에서는 수중 운동체에 대한 6자유도 운동방정식과 동유체력 모델링 기법이 제시된다. 3절에서는 유체력 미계수 결정에 활용된 CFD 시뮬레이션에 대한 내용과 최소자승법으로 유체력 미계수를 결정하는 과정이 기술된다. 4절에서는 결정된 유체력 미계수를 검증하기 위해 수행된 L형, U형 그리고 S형 선회 시나리오에 대한 6자유도 운동해석 조건 및 결과가 제시된다. 마지막으로 5절에서는 본 연구에 대한 결론으로 마무리 된다.
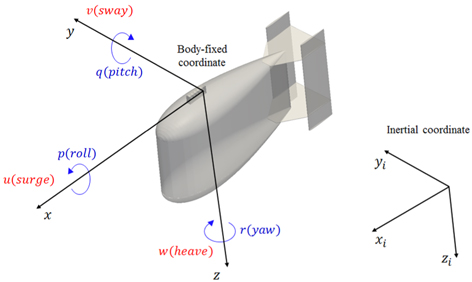
3차원 공간상에서 수중 운동체의 6자유도 운동을 표현하기 위하여 Fig. 1과 같이 물체고정좌표계와 관성좌표계가 활용된다. 일반적으로 수중 운동체의 물체고정좌표계 원점은 부력중심으로 설정되지만, 수중 예인체의 경우 예인 케이블과 연성되어야 되기 때문에 본 연구에서 물체고정좌표계 원점은 Fig. 1과 같이 예인점(Towing point)으로 설정된다. 물체고정좌표계에서 수중 운동체의 속도는 식 (1)과 같이 표현되며, 관성좌표계에서 수중 운동체의 위치 및 자세는 식 (2)와 같이 표현된다.
여기서 ν1과 ν2는 각각 물체고정좌표계에서 수중 운동체의 병진속도와 각속도를 정의하는 벡터이다. η1과 η2는 각각 관성좌표계에서 수중 운동체의 위치 및 오일러 각을 나타내는 벡터이다.
식 (3)과 같이 물체고정좌표계에서 계산된 결과는 변환행렬J(η)을 통해 관성좌표계에 대한 값으로 변환된다. 변환행렬은 zi(ψ)축, yi(θ)축 그리고 xi(ϕ)축 순으로 회전하는 경우에 대하여 식 (4)와 같이 정의된다.
여기서 s(•), c(•), t(•)는 각각 sin(•), cos(•), tan(•)를 의미한다. 물체고정좌표계에서 수중 운동체의 6자유도 운동방정식은 식 (5)-(10)과 같다(Fossen, 1994; Fossen, 2011; Go et al., 2016a; Go et al., 2016b).
여기서 m과 Iij는 각각 수중 운동체의 질량과 관성모멘트이며 xg, yg, zg는 수중 운동체의 무게중심 좌표이다. X, Y, Z, K, M, N은 본 논문의 주요 관심사인 동유체력을 포함하는 모든 외력을 의미한다.
6자유도 방향에 대한 동유체력은 다음과 같이 정의된다.
동유체력은 물체의 움직임에 의해 발생하는 유체력이기 때문에 물체의 가속도와 속도에 대한 함수라고 정의할 수 있다. 따라서 가속도와 속도에 대하여 동유체력을 Taylor-series 전개하면 수학적인 모델링이 가능하다. 이러한 접근방법이 동유체력을 모델링하는데 적용되는 핵심적인 아이디어이다. 동유체력을 1차 미분 항까지 Taylor-series 전개하여 선형화된 모델을 활용하는 것이 가장 기본적인 방법이다. x방향 동유체력을 가속도와 속도에 대하여 1차 미분 항까지 Taylor-series 전개하게 되면 식 (12)와 같이 나타낼 수 있다.
여기서 가속도와 속도 항 앞에 곱해져 있는 항들은 유체력에 대한 미분계수로서 유체력 미계수(Hydrodynamic derivatives)라 정의되며, 가속도와 속도 항 앞에 곱해져 있는 미분계수를 각각 부가질량과 감쇠계수로 정의한다. 일반적으로 유체력 미계수는 보다 효율적인 표기를 위해 식 (13)과 같이 미분변수를 아래첨자로 하여 나타내어진다. 이와 같은 형태가 가장 많이 쓰이고 잘 알려진 유체력 미계수 표기법이다.
식 (13)과 같은 방법으로는 동유체력의 비선형성을 고려할 수 없다. 따라서 비선형성을 고려할 수 있는 모델링 방법이 적용되어야 한다. 본 연구에서는 비선형화 기법으로 물리적인 현상을 보다 더 효과적으로 표현 가능한 것으로 알려져 있는 Second-order modulus 전개방법(Fedyaevsky and Sobolev, 1963)을 활용하여 동유체력을 모델링하였다(Clarke, 2003). Second-order modulus 전개를 통해 동유체력은 식 (14)와 같이 모델링된다.
식 (14)를 하나의 시스템으로 표현하면 식 (15)와 같다.
여기서 Ma는 부가질량 행렬, Dl은 선형 감쇠계수 행렬 그리고 Dn(ν)은 비선형 감쇠계수 행렬이며, 6자유도 운동해석을 위해 결정되어야하는 유체력 미계수는 총 108개이다. 본 연구에서 Ma는 포텐셜 이론에 근거한 이론적인 방법(Son et al., 2006; Go et al., 2016a)으로 결정하고, Dl과 Dn(ν)은 CFD 시뮬레이션으로 결정하였다.
본 연구에서는 CFD 해석을 위해 상용 프로그램인 FLUENT를 사용하였다. 유체의 지배방정식은 비압축성 Navier-Stokes 방정식이며, 이를 FLUENT를 통해 셀 중심 유한체적기법으로 해석하였다. 식 (16)-(17)은 각각 지배 방정식을 구성하는 연속방정식과 운동량 방정식을 아인슈타인 표기법으로 나타낸 것이다.
여기서 ρ, V, P그리고 f는 각각 유체의 밀도, 속도, 압력 그리고 유체에 작용하는 외력을 뜻한다. μ는 유동의 전체 점성계수로 μ = μl +μt, 즉 유체 자체의 물성에 따라 결정되는 층류점성계수 μl과 평균유동에 추가적인 비정상 와류에 의하여 발현되는 난류점성계수 μt의 합으로 정의된다. 본 연구에서 μt는 k-ω SST(Shear-stress transport) 난류모델을 통해 결정된다. 유체의 속도와 압력은 SIMPLE(Semi-implicit method for pressure linked equation) 알고리즘으로 연성된다.
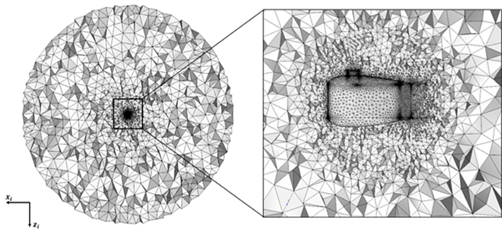
전체 계산영역은 예인체의 기하학적 중심을 중심으로 하고 지름이 예인체 길이의 100배인 구로 설정하였다. 입구 유동조건은 속도에 대한 Dirichlet 조건을 적용하였고, 출구는 Pressure outlet으로 지정하였다. 격자는 상용 프로그램인 POINTWISE를 사용하여 생성하였다. 예인체의 표면을 비정렬 격자로 구성하고 계산영역에 대하여 비정렬 사면체 격자를 생성하였다. 격자생성 결과는 Fig. 2와 같다.
CFD 해석을 통해 유체력 미계수를 결정하기 위해서는 다양한 조건에 대한 해석이 필요하다. 해석 케이스는 수중 운동체의 실제 운용조건을 기준으로 설정되었다. 본 연구에서는 수중 예인체의 운용조건을 바탕으로 기준 움직임은 직진운동으로 설정하고, 기준속도는 운용속도로 지정하였다. 이를 토대로 직진 운동의 방향 및 회전축의 방향을 변화시켜가면서 해석 케이스를 결정하였고, 정상상태에 대한 CFD 해석을 수행하였다. CFD 해석에서 물체의 병진운동은 고정된 물체에 상대속도로 유체가 유입되도록 하여 나타내었고, 회전운동은 MRF(Moving reference frame) 기법으로 표현하였다.
선형 및 비선형 감쇠 계수는 CFD 계산결과를 최소자승법으로 커브피팅하는 방식으로 결정된다. 본 연구에서 수행한 CFD 해석은 정상상태에 대한 해석이기 때문에 가속도와 관련된 항은 무시된다. 따라서 정상상태에 대한 동유체력 모델링 식은 식 (18)과 같이 정의된다.
따라서 x방향에 대하여 다음과 같은 관계식이 성립된다.
여기서 아래첨자로 표현된 숫자는 CFD 해석케이스의 순번을 의미하고 n은 CFD 해석 케이스의 총 계수를 나타낸다. A는 CFD 해석조건인 수중 운동체의 속도로 구성된 n×12 행렬이고 b는 CFD 해석을 통해 얻은 x방향 힘으로 구성된 n×1 벡터이다. h는 예인체의 선형 및 비선형 감쇠계수로 구성된 12×1 벡터이다. A와 b는 각각 CFD 해석의 입력 값과 결과 값으로 구성요소를 이미 알고 있는 행렬 및 벡터이다. h는 식 (19)를 통해 구해야하는 미지수 벡터이다. 본 연구에서 식 (19)는 미지수의 수보다 방정식의 수가 많은 시스템이다. 따라서 식 (19)를 해석하기 위해서는 식 (20)과 같이 정규연립방정식(Normal system)으로 변환되어야 한다.
식 (19)의 양변에 AT를 곱해줌으로써 식 (20)은 미지수와 방정식의 수가 동일한 정규연립방정식이 된다. 따라서 미지수 벡터 h는 다음과 같이 결정된다.
이러한 일련의 과정을 최소자승법이라고 한다. 나머지 방향에 대한 선형 및 비선형 계수도 동일한 방식으로 결정하면 된다.
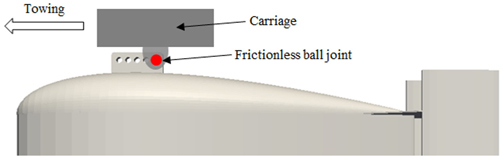
결정된 유체력 미계수의 물리적인 타당성을 검증하기 위해 가상 시나리오에 대한 6자유도 운동해석을 수행하였다. 수중 예인체의 독자적인 운동특성을 파악하기 위하여 본 해석에서는 케이블이 아닌 캐리지에 의해 예인되는 상황을 가정하였다. Fig. 3과 같이 캐리지는 예인체 상단에 위치하는 마지막 예인점(Towing point)과 마찰이 없는 볼 조인트로 체결된다. 따라서 예인체의 병진운동은 캐리지와 동일하게 발생하게 되고, 회전운동은 구속조건 없이 자유롭게 발생하게 된다.
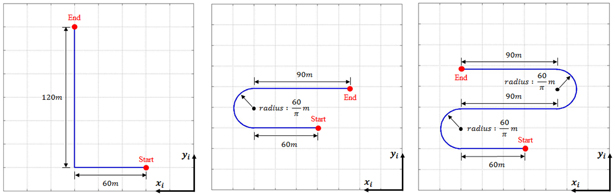
본 해석에서 캐리지는 Fig. 4에 제시된 세가지 시나리오의 경로에 따라 3m/s의 일정한 속력으로 움직이게 된다. 세 가지 예인 시나리오는 다양한 관점에서 예인체의 운동특성을 파악하기 위하여 L형(90도) 선회, U형(180도) 선회 그리고 S형(360도) 선회로 구성된다. L형 선회는 경로의 방향이 순간적으로 90도 변화되기 때문에 실제 운용단계에서 수행될 수 없는 가혹한 조건의 기동이지만 본 논문에서는 수치해석 기법의 강건성을 보여주기 위해 해석 시나리오로 활용되었다.
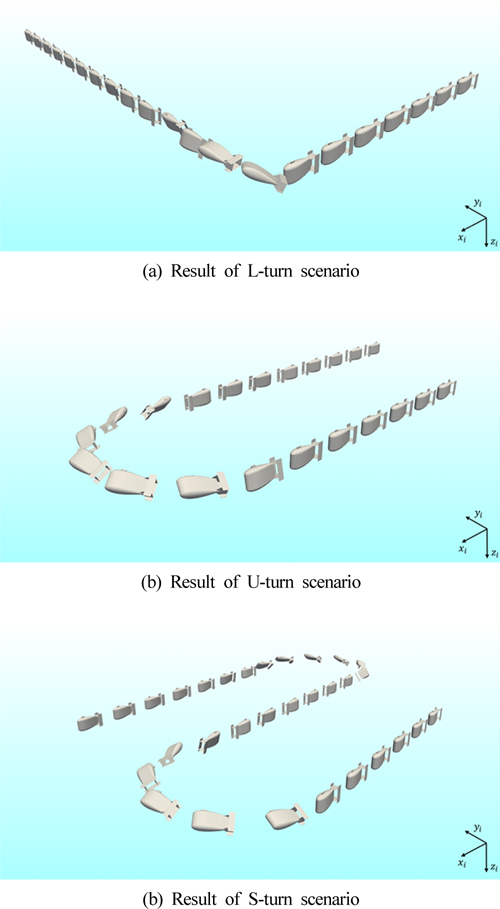
6자유도 운동해석 결과는 Figs. 5-6과 같이 시간에 따른 예인체의 오일러 각 변화 그래프와 스냅 샷으로 제시된다. L형 선회와 U형 선회는 총 21개의 스냅 샷으로 나타내었고, S형 선회는 경로가 상대적으로 길기 때문에 31개의 스냅 샷으로 나타내었다. 스냅 샷에서 제시된 예인체의 크기는 자세변화를 보다 명확하게 구별하기 위하여 2배로 확장하여 나타내었다.
세 가지 시나리오는 모두 직진코스로 시작된다. Fig. 5를 통해 예인체의 자세변화가 첫 번째 직진코스에서 정상상태로 돌입하는 것을 확인할 수 있다. 정상상태에서 예인체의 오일러 각은 횡동요(Roll), 종동요(Pitch), 선수동요(Yaw) 순으로 각각 •0.6도, 0.18도, 0.3도이다. 예인체의 형상은 좌우대칭이며 예인점이 몸체의 상단에 위치하고 있기 때문에 직진 예인시 종동요 각을 제외한 나머지 각들은 모두 0도가 나와야 한다고 판단될 수 있다. 본 연구에서는 유체의 비선형성이 고려된 CFD 해석을 통해 유체력 미계수를 결정하였으며, 6자유도 방향에 대한 유체력 미계수가 모두 고려되었기 때문에 직진코스임에도 불구하고 횡동요 각과 선수동요 각이 모두 0이 아닌 특정 값을 가지고 있는 것으로 판단된다. 그러나 그 크기는 1도 미만으로 무시될 수 있을 만큼 매우 작기 때문에 실제 예인체의 거동을 예측하는데 큰 영향을 미치지 않는다. 이러한 현상을 통해 CFD 해석을 통해 유체력 미계수를 결정하고 동유체력 모델링에 일체의 가정이나 단순화가 고려되지 않았다는 본 연구의 차별성을 확인할 수 있다.
Fig. 5-(a)와 같이 L형 선회가 시작하게 되면 예인체의 자세변화가 급격하게 발생한다. 예인체의 진행방향이 수직으로 꺾이기 때문에 예인체의 횡동요 각이 최대 120도 이상까지 발생하게 되는 것을 확인할 수 있다. 또한, 기존 운동방향에 대한 예인체의 속도가 순간적으로 0이 되기 때문에 관성에 의해 머리올림(Nose up) 방향으로 종동요 각이 약 30도까지 증가하는 것을 확인할 수 있다. 선수동요 각은 진행방향과 동일하게 90도로 수렴해 나가게 된다. 선회가 끝나게 되면 다시 직진코스가 시작되기 때문에 횡동요 각과 종동요 각은 첫 번째 직진코스에서 나타난 값으로 수렴하게 되고 선수동요 각은 약 90도에 수렴한 것이 확인된다.
U형 선회는 일정한 반경을 기준으로 수행되기 때문에 L형 선회에 비해 자세변화가 부드럽게 발생하게 된다. Fig. 5-(b)를 통해 U형 선회가 수행되는 동안 선회중심으로 향하는 속도성분이 발생하여 예인체의 횡동요 각이 선회 중심과 반대되는 방향으로 증가하는 것을 확인할 수 있다. 이와 더불어 예인체가 U형 선회를 절반이상 수행하게 되면 평형상태가 되어 일정한 자세로 나머지 선회를 마무리 하게 되는 것을 확인할 수 있다. 두 번째 직진코스가 시작되면 선수동요 각은 약 180도로 수렴하게 되고 나머지 오일러 각들은 첫 번째 직진코스의 값과 동일해진다. S형 선회는 두 번의 U형 선회가 서로 반대방향으로 수행되는 상황으로 첫 번째 U형 선회와 두 번째 U형 선회시 발생하게 되는 자세변화가 대칭적인 것을 Fig. 5-(c)를 통해 확인할 수 있다.
세 가지 시나리오에서 발생하는 예인체의 자세변화는 Fig. 6을 통해 보다 명확하게 파악할 수 있으며, 이를 통해 각 시나리오 별로 발생하게 되는 예인체의 운동특성이 물리적인 직관과 매우 유사함 확인할 수 있다.
본 연구에서는 수중 예인체에 작용하는 동유체력을 Second-order modulus 전개로 모델링하고, 이를 구성하는 부가질량과 감쇠계수(선형, 비선형)를 각각 이론적인 접근방법과 CFD 시뮬레이션으로 결정하였다. 선형 및 비선형 감쇠계수를 결정하기 위해 수중 예인체의 실제운용조건을 기준으로 CFD 해석 케이스를 설정하였고, CFD 해석을 통해 예측된 수중 예인체에 작용하는 6자유도 힘과 모멘트를 동유체력 모델링 식으로 커브피팅 하였다. 커브피팅 과정에는 최소자승법이 사용되었고, 이와 같은 과정을 통해 모든 선형 및 비선형 감쇠계수를 결정할 수 있었다. 본 연구의 타당성을 검증하기 위해 결정된 유체력 미계수를 적용하여 L형, U형 그리고 S형 선회 시나리오에 대한 6자유도 운동해석을 수행하였다. 이상의 연구를 통해 다음과 같은 결론을 내릴 수 있다.
첫째, 구속모형시험과정 없이 오로지 CFD 시뮬레이션만으로도 유체력 미계수를 결정할 수 있음을 확인할 수 있었다. 둘째, 본 연구에서 제시한 기법은 PMM, RA 시험과 같은 복잡한 구속모형시험과정을 시뮬레이션 상에서 구현하지 않아도 되기 때문에 기존 연구들에서 제시한 기법에 비해 보다 효율적으로 유체력 미계수를 결정할 수 있다. 또한, 동유체력 정식화 과정에 필요한 모든 유체력 미계수를 결정할 수 있다. 마지막으로, 세 가지 다른 시나리오에 대한 6자유도 해석결과가 물리적인 직관과 매우 유사함을 확인할 수 있었으며, 이를 통해 결정된 유체력 미계수의 물리적인 타당성을 검증할 수 있었다.
References
Ahn, J.H., Jung, C.H.. (A Study on the Analysis of Underwater Behaviors of Two Bodies Having Different Weight Characteristics, Journal of the Korea Society for Simulation, 2012). 21(1):35-43.


Clarke, D.. (The foundations of steering and maneuvering Proceedings of International Federation of Automatic Control Conference on Control Applications, Melbourne Australia, Plenary talk Melbourne Australia: 2003.
Fedyaevsky, K.K., Sobolev, G.V.. (Control and Stability in Ship Design State Union Shipbuilding Industry Publishing House, Leningrad: 1963.
Fossen, T.I.. (Guidance and Control of Ocean Vehicles John Wiley & Sons Ltd., Chichester: 1994.
Fossen, T.I.. (Handbook of Marine Craft Hydrodynamics and Motion Control John Wiley & Sons Ltd., Chichester: 2011.
Go, G., Lee, E., Ahn, H.T., Kim, S., Chun, S.Y., Kim, J.S., Lee, B.H.. (6DOF Simulation and Determination of Hydrodynamic Derivatives of Underwater Tow-Fish Using CFD, Journal of the Society of Naval Architects of Korea, 2016a). 53(4):315-328 10.3744/SNAK.2016.53.4.315.


Go, G., Lee, E., Ahn, H.T.. (3D Nonlinear Fully Coupled Simulation of Cable and Tow-fish System, Journal of Ocean Engineering and Technology, 2016b). 30(6):458-467 10.5574/KSOE.2016.30.6.458.


Pan, Y., Zhang, H., Zhou, Q.. (Numerical Prediction of Submarine Hydrodynamic Coefficients Using CFD Simulation, Journal of Hydrodynamics, 2012). 24(6):840-847 10.1016/S1001-6058(11)60311-9.

Son, K.H., Lee, S.K., Ha, S.P.. (Mathematical Model for Dynamics of Manta-type Unmanned Undersea Vehicle with Six Degrees of Freedom and Characteristics of Maneuverability Response, Journal of the Society of Naval Architects of Korea, 2006). 43(4):399-413 10.3744/SNAK.2006.43.4.399.


Santhakumar, M., Asokan, T., Sreeram, T.R.. (Analysis of Parameter Sensitivity Using Robust Design Techniques for a Flatfish Type Autonomous Underwater Vehicle, International Journal of Quality, Statistics, and Reliability, 2009). 1-10.


Shadlaghani, A., Mansoorzadeh, S.. (Calculation of Linear Damping Coefficients by Numerical Simulation of Steady State Experiments, Journal of Applied Fluid Mechanics, 2016). 9(2):653-660 10.18869/acadpub.jafm.68.225.24342.

- TOOLS
-
METRICS

-
- 2 Crossref
- Scopus
- 8,823 View
- 153 Download
- Related article in JOET
-
Prediction of Hydrodynamic Coefficients for Underwater Vehicle Using Rotating Arm Test2016 ;30(1)