CEL기법을 이용한 앵커 끌림 시뮬레이션에 의한 Rock-berm 설계
Design of Rock-berm by Anchor Dragging Simulation using CEL Method
Article information
Abstract
In this study, an anchor dragging simulation was performed using the CEL method to design a rock-berm, which is a protection method for submarine cables. In order to simulate an anchor drag, preliminary simulations were first performed to determine the initial anchor penetration depth, anchor drag velocity, drag angle, and distance between the anchor and rock-berm. Based on the preceding simulation results, a safe rock-berm design for protecting the submarine cables was simulated to calculate the anchor penetration depth by the anchor dragging. As a result, the penetration depth of the anchor was found to be shallower in a hard seabed, and the penetration depth was deeper in a soft seabed. , the height of the rock-berm was determined according to the physical properties of the seabed.
1. 서 론
최근 육지와 도서간 혹은 국가와 국가를 잇는 전력망과 해상 풍력단지의 수요가 증가함에 따라 그에 비례하여 해저케이블(Submarine cable)에 대한 수요가 증가하고 있는 추세이다. 뿐만 아니라 이 같은 해저에 설치되는 케이블은 세계 해양을 연결하여 위성통신과 함께 통신 발전에 크게 이바지 하고 있으며, 그 수요는 앞으로 더욱 증가 할 것으로 예상된다.
하지만 해저에 설치되는 케이블은 육상에 비해 보다 열악한 환경에 노출되어 있어 가동 중 손상을 입을 가능성이 매우 높다. 특히 해저케이블의 외력에 의한 손상 중 가장 큰 위해요인은 어로 활동으로 그중 70% 정도가 크고 작은 어선의 앵커로 인해 수심 200m 이내에서 가장 많이 발생하고 있다(Jung et al., 2007). 그 사례로 2006년 제주도와 해남을 잇는 해저케이블이 외력에 의한 손상으로 제주도 전역에 정전사태가 발생하였고 이는 선박용 앵커 충돌이 원인으로 추정되었다. 이처럼 해저케이블은 안강망 조업 및 새우조망과 같은 어구활동이 활발한 지역과 선박 통행량이 많은 주 항로에 설치되어 사고위험에 항시 노출되어 있다. 해저케이블뿐 아니라 해저파이프라인에 대한 사고 시나리오도 앵커의 끌림 및 저인망 어업활동으로 인해 주로 발생한다(Liu et al., 2013). 또한 Det norske veritas(DNV) RP-107에 따르면, 해저에 설치되는 파이프라인 및 케이블에 대해 손상을 줄 수 있는 것들을 정의하고 설계 시 이들을 고려하도록 권장하고 있으며, 그중 선박용 앵커를 중대한 위험요소 중 하나로 분류하고 있다. 이러한 케이블의 사고로 인한 인명사고 및 환경 오염, 그리고 막대한 경제적 손실의 예방을 목적으로 해양 설비의 설치 및 운영에 대한 엄격한 안전 규제가 요구된다(DNV, 2010).
따라서 해저케이블을 안정적으로 가동하기 위해서는 다양한 충돌 외력으로부터 케이블을 안전하게 보호해야 한다. 이를 위해 해저지반(Seabed)을 굴착하여 매설하는 트렌칭⋅백필링(Trenching and backfilling)시스템이 많이 적용되고 있으며, 락범(Rock-berm)과 보호구조물로 피복하는 등의 다양한 보호공법이 적용되고 있다. 보호공법에 관한 국내 연구는 앵커 충돌 및 끌림에 의한 원통 연결 보호구조물의 최대 응답 해석(Woo and Na., 2010)과 SPH(Smooth particle hydrodynamic)기법을 이용하여 해저지반이 고려되지는 않았지만 락범에 대한 낙하하는 앵커의 충돌 시뮬레이션(Woo et al., 2014)이 수행되는 등 보호공법에 관한 연구가 국내에서도 활발하게 진행되어왔다. 하지만 실제 조업 시 사용되는 앵커와 운항하는 선박의 앵커는 낙하에 의한 충돌 보다 끌림에 의한 충돌을 더 큰 위해요소로 분류하고 있다(DNV, 2010). 그러나 해저지반과의 상호작용을 고려한 앵커 끌림에 의한 충돌 안정성에 관한 연구와 그 결과에 따른 보호 공법인 락범 설계 기준이 없는 실정이다.
따라서 본 연구에서는 해저지반과 앵커 그리고 보호공법인 락범의 상호작용을 고려하여, 앵커의 끌림을 고려한 락범 설계를 제안 하고자 한다. 이를 위해 선박으로부터 투하된 앵커가 조류 및 앵커 회수에 의한 영향으로 발생되는 끌림으로 인해 해저지반 내 매설된 케이블과 충돌하면 케이블은 파괴 및 오작동이 예상되므로 안전하지 않다는 해석상 설정을 하였다. 시뮬레이션에 사용된 선박용 앵커는 스톡리스 앵커(Stockless anchor)이며, 사용된 해석 기법은 Abaqus/Explicit의 CEL(Coupled eulerian lagrangian)방법을 적용하였다. 이를 이용한 끌림 해석(Dragging analysis)을 실시하여, 끌림에 의해 해저지반내로 앵커가 침투하는 깊이를 산정하고, 락범으로 보강하였을 때 앵커가 침투되는 깊이와 비교하여 최종적으로 해저지반 성질에 따른 안전한 락범 설계를 제안하고자 한다.
2. 3차원 유한요소 모델링
2.1 CEL기법을 이용한 대변형 해석
FEM(Finite element method)은 토목 및 기초공학 분야에서 다양하게 활용되어져 왔으며, 특히 지반-구조물 상호작용을 고려한 거동 분석을 모사하는 중요한 도구로 사용되어져 왔다. 하지만 앵커 끌림과 같은 대변형(Large deformation)이 발생되는 해석에는 격자(Mesh)의 왜곡(Distortion) 현상과 접촉면 문제 등으로 인해 경계조건을 풀어내는데 한계가 있다(Kim and Jeong., 2014). 따라서 본 연구에서는 이러한 대변형 문제를 해석하기 위한 대체 해석법인 CEL(Coupled eulerian lagrangian)기법을 사용하여 앵커 끌림 해석을 수행 하고자 한다.
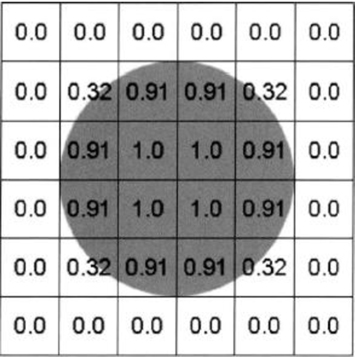
CEL 기법이란 연속체의 거동을 물체의 좌표 및 시간으로 정의하여 주로 구조 및 지반 공학의 해석에 사용되는 Lagrangian 모사법과 공간 좌표 및 시간으로 정의하여 주로 유체역학의 해석에 사용되는 Eulerian 모사법을 합친 것으로, Eulerian으로 모사된 영역내의 Lagrangian 요소의 거동을 각 요소의 체적비인 EVF(Eulerian volume fraction)로 나타내며, Fig. 1(ABAQUS user's manual)과 같이 각각의 Eulerian element는 물성이 채워져 있는 비율로 표현된다. 이러한 Eulerian 모사법의 장점을 바탕으로 대변형에 대한 비틀림이나 왜곡 없이 해저지반 대변형에 의한 앵커 거동 모사가 가능하다. 실제로 CEL기법을 이용한 대변형에 관한 연구가 다양하게 수행되어져 왔으며, CEL해석기법의 대변형 해석적용에 대한 검증이 이루어졌다(Qiu et al., 2011). 또한 CEL기법을 적용하여 락범은 고려하지 않은 상태에서의 모형앵커 끌림의 영향에 관한 Case별 수치해석 연구(Zhao and Liu., 2015)등이 수행되었다.
2.2 유한요소 모델링
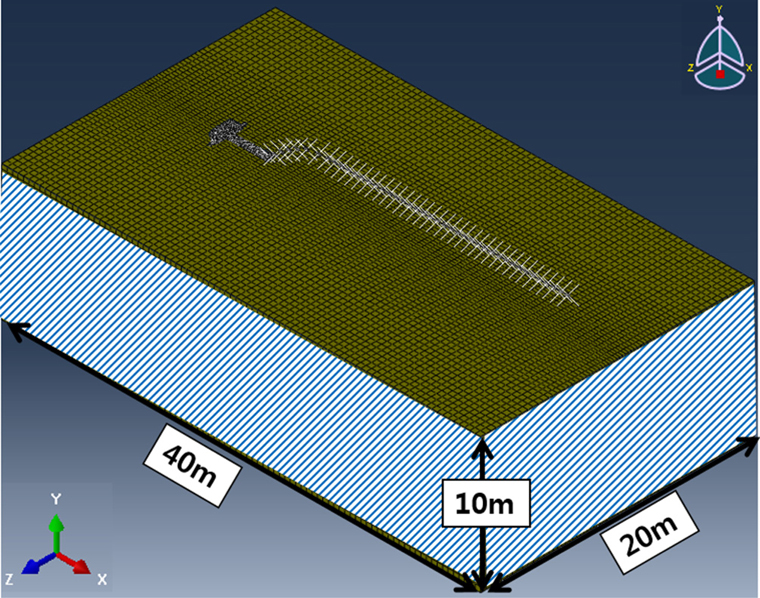
3차원 유한요소 모델링을 위해 Abaqus/Explicit를 이용하여 Fig. 2와 같이 해저지반과 락범을 Eulerian으로 모델링하고, 앵커와 앵커를 연결하는 체인은 Lagrangian으로 모델링 하였고, 약 25만개의 격자가 사용되었다. 경계조건 설정은 모델링된 해저 지반 하단부의 법선방향(Y축) 변위와 모델링된 해저지반 옆면의 접선방향(X, Z축) 변위를 구속하는 조건을 적용하였다.
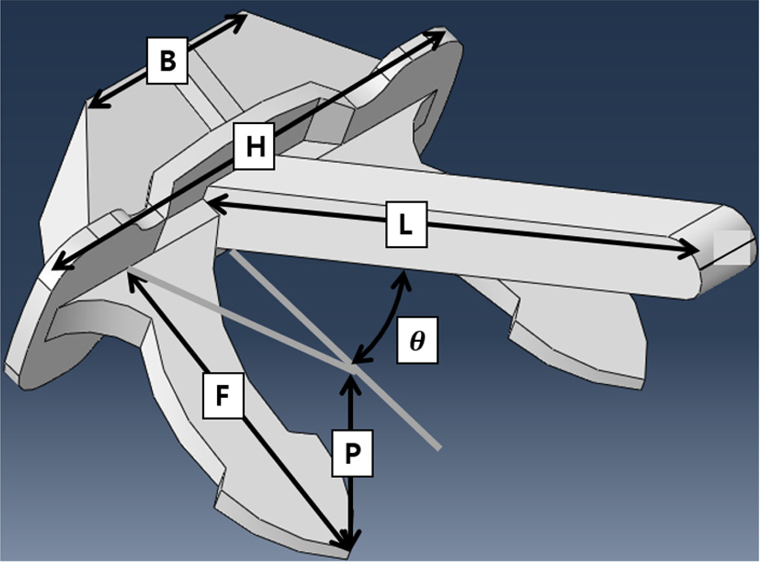
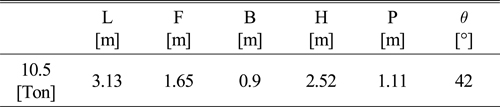
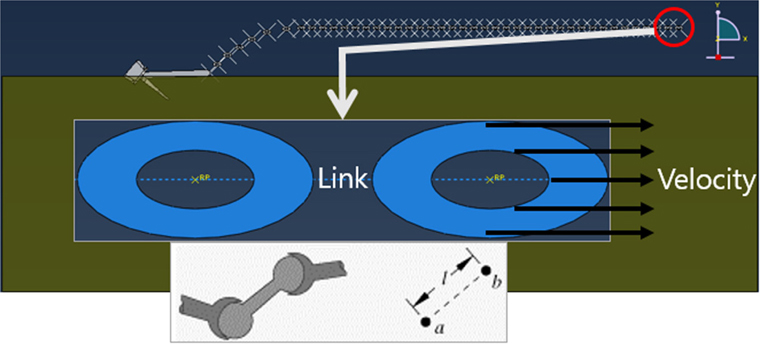
앵커는 10.5ton의 스톡리스 앵커(Stockless anchor)를 선정하여 (SPS-KSA-V3311-5978, 2014) Fluke의 최대 각도인 42°로 모델링하고 강체(Rigid body)로 설정하였으며, 형상은 Fig. 3에 나타내었고 앵커의 제원은 Table 1에 나타내었다. 앵커 체인(Anchor chain)은 Fig. 4와 같이 각각의 체인을 강체로 모델링 한 후 체인과 체인을 연결하는 Link type의 wire로 연결하여, 연결부의 회전을 제어하는 설정을 적용하였다.
해석의 단계(Analysis step)는 1단계에서 해저지반의 초기 토압을 고려하기 위해 중력을 적용하여 안정화 작업을 수행하였고, 2단계는 앵커 체인을 해저지반에 안착시키는 작업을 수행하였고, 마지막 3단계에서는 앵커 체인 연결부 제일 끝 부분에 속도를 주어 앵커가 끌릴 수 있게 설정하였다.
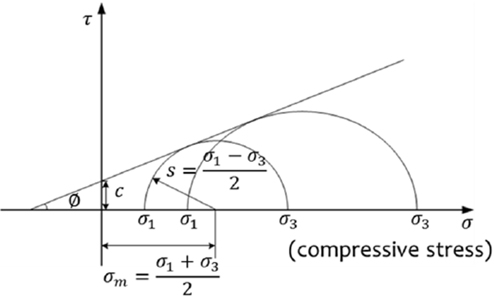
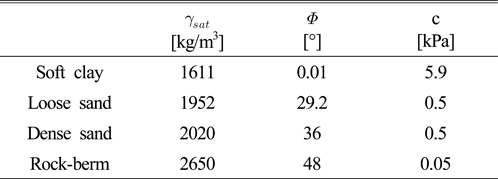
또한 해저지반은 느슨한 모래(Loose sand)와 조밀한 모래(Dense sand) 그리고 연약점토(Soft clay) 총 3가지를 고려하였으며, 변형이 가능한 탄소성체(Elastic-plastic)로 해석에 사용된 해저지반 및 락범에 적용되는 역학적 물성은 다양한 항복기준(Failure criteria)중 재료의 파괴 시 응력이 응력원의 포락선으로 나타나는 Mohr의 파괴 기준과 점착력(Cohesion, c)과 내부마찰각(Friction angle, Φ)의 강도정수를 포함한 직선관계를 갖는다는 Coulomb의 기준을 합성한 Mohr-Coulomb 구성모델을 적용하여 락범과 해저지반을 조성하였다. 일반적인 Mohr-Coulomb의 항복 기준을 Fig. 5에 나타내었고, 적용된 해저지반과 락범의 역학적 물성을 Table 2에 나타내었다(Das, 2009).
3. 해석 시나리오 설정
3.1 해석 시나리오 설정
앵커 끌림 수치 시뮬레이션을 실시하기 위해 끌림 시나리오에 대한 설정은 다음의 순서로 진행하였다. 앵커는 해저지반에 침투하여 해양에서 선박 및 구조물을 정점에 계류시키기 위한 장치이다. 하지만, 다양한 해양환경과 선박의 제원에 의해 끌림에 관한 기준 설정이 모호하다. 따라서 Fig. 6과 같이 모든 설정의 추론 값과 가정이 요구되며, 본 연구에서는 매우 보수적인 시나리오를 설정 하고자 한다.
3.2 시나리오 설정을 위한 선행해석
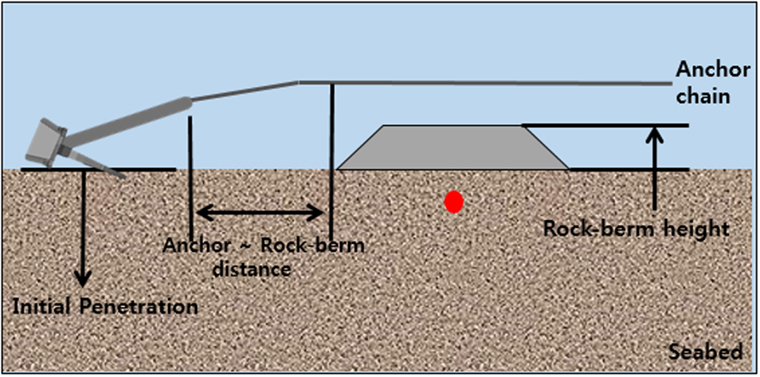
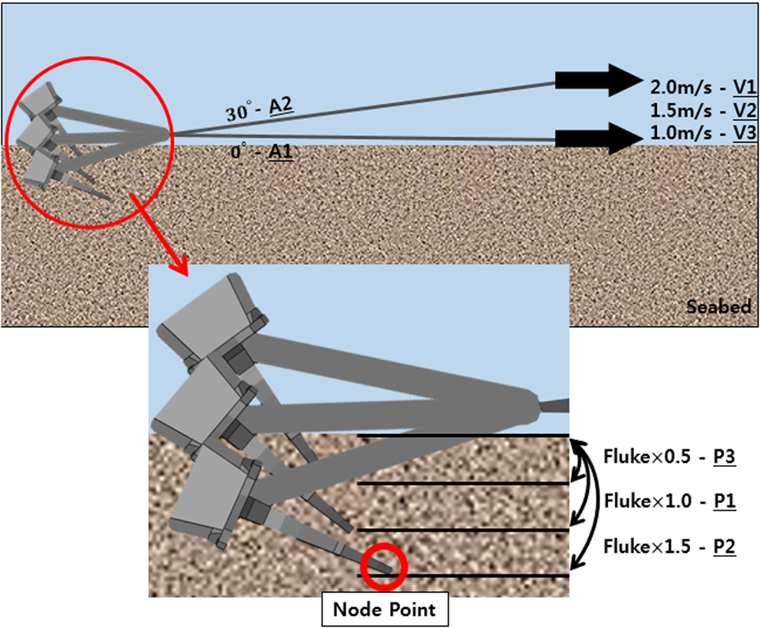
앵커 끌림 시나리오 설정을 위해 락범으로 보강되지 않은 해저지반에서의 앵커 초기 침투깊이(Initial penetration)설정, 앵커 끌림 속도(Drag velocity) 및 끌림 각도(Drag angle) 설정, 그리고 앵커와 락범의 이격거리(Anchor- rock-berm distance)설정을 위한 선행해석을 실시하였다. 선행해석에서 고려된 설정 값들을 Fig. 7에 나타내었으며, Fig. 7과 같이 먼저 앵커의 초기 지반 침투깊이에 대한 설정은 앵커가 낙하(Drop)하여 해저지반에 충돌 시 해저지반의 변위는 0.074m ~ 0.351m까지 지반 물성치와 앵커의 중량에 따라 결과 차이를 보였으며(Shin and Seo., 2017), 해저지반에 나타나는 변위가 곧 앵커가 지반에 침투되는 깊이가 된다. 또한 단단한 지반일수록 앵커가 침투되는 깊이는 얕을 것이며, 앵커가 낙하되어 해저지반에 안착 후 앵커는 지반내로 시간이 지남에 따라 더 깊게 침투할 것으로 예상된다.
따라서 초기 침투깊이 설정을 위해 앵커 Fluke(Fig. 3의 F)이 해저지반에 침투해 있는 상태(P1)와 Fluke의 1.5배(P2), 0.5배(P3)의 초기 침투깊이를 설정하여 해석을 수행하여 비교하였다. 둘째로, 침투되어 있는 앵커가 끌리는 속도와 각도에 대한 설정이 필요하다. 앵커가 끌리는 속도 및 각도에 따라 해저지반내로 침투하는 깊이에 대한 차이가 나타났으며(Zhao and Liu., 2015), 본 연구에서는 앵커 끌림 속도에 따른 비교를 위해 통상 선박이 앵커를 회수하는 속도와 비슷한 2m/s(V1), 1.5m/s(V2), 1m/s(V3)로 설정하였고 또한 끌림 각도를 0°(A1)과 30°(A2)를 비교하여 해석을 수행하였다. 마지막으로, 앵커와 락범의 이격거리에 대한 설정이 필요하며, 이는 모든 선행해석 결과를 분석하여 이격거리를 산정하였다. 앵커 침투깊이 측정은 각 Case별 끌림 시 앵커 최하단부인 Fluke 끝부분 Node point의 궤적을 추적하여 산정하였다. 또한 본 절의 선행 해석은 앵커 끌림에 의한 락범 설계 해석 시 적용돼야하는 시나리오 설정을 위해 진행되었으므로, 선행 해석에서 고려한 해저지반은 3가지로 분류된 지반 물성치 가운데 중간의 강도를 갖는 느슨한 모래를 사용하였다.
3.3 선행해석 결과 분석 및 시나리오 결정
먼저 끌림 각도를 설정하기 위해 초기 침투깊이의 P1과 끌림 각도 A1, A2에 따른 끌림 속도 별 지반 침투깊이 결과를 Fig. 8(a)에 나타내었다. 끌림 각도에 따라 앵커가 지반내로 침투하는 깊이 결과에 많은 차이를 보였으며, 본 연구에서는 보수적인 설정 값을 사용하여 락범 설계를 하고자 끌림 각도는 A1으로 결정하였다. 또한 초기 침투깊이와 끌림 속도를 결정하기 위해 끌림 각도 A1을 적용한 초기 침투깊이 P2, P3에 따른 끌림 속도별 앵커의 지반 침투깊이 결과를 Fig. 8(b), (c)에 나타내었다. 결과를 보면 앵커의 초기 침투깊이 설정을 변경 할수록 끌림에 의한 침투깊이는 끌림 거리에 따라 차이를 보이지만, 끌림 거리 8m 이상에서의 초기 침투깊이 P1, P2, P3에 대한 오차율은 2~5% 대로 비교적 적은 영향을 받는 것을 알 수 있었다. 또한 끌림 속도는 V1일 때는 얕게 침투 하는 결과가 나타났으나, 마찬가지로 끌림 거리 8m 이상의 거리에서 속도 V2와 V3의 결과비교 시 전체적으로 3~6%대로 속도에 의한 차이 또한 비교적 적은 것으로 나타났다.
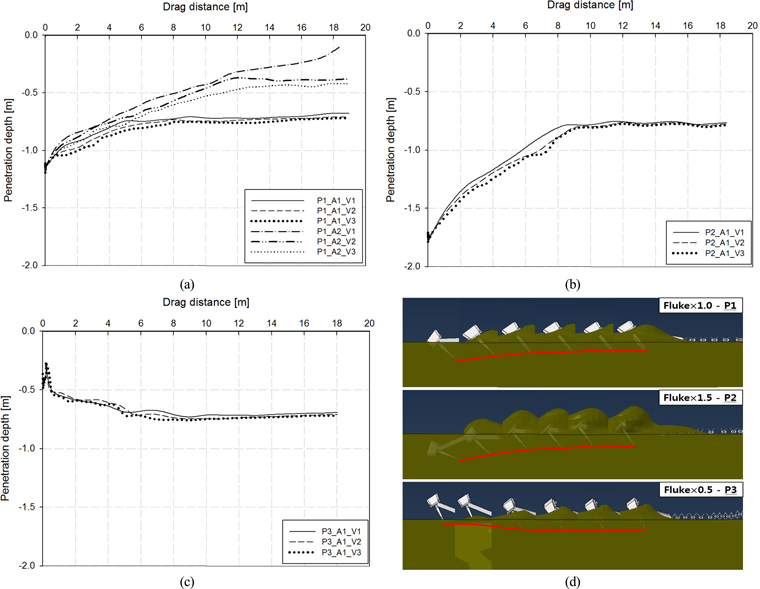
Preceding simulation results of anchor trajectory at different initial penetration, drag velocities and drag angles
따라서 앵커의 초기 침투깊이는 Fluke이 해저지반에 완전 침투해있는 상태(P1)로, 끌림 속도는 1.5m/s(V2)로 결정하였다. 앵커와 락범의 이격거리는 Fig 8(a) P1의 결과와 Fig 8(b) P2의 결과의 경우 앵커 끌림에 의해 침투깊이가 점차 얕아지고 끌림 거리 8m 이후 침투깊이가 일정해지는 경향을 보였으며, 이는 끌림 거리 8m 이전 해저케이블과 충돌해야 보수적인 설정임을 나타내고 있다. 반대로 Fig 8(c) P3의 결과는 앵커 끌림에 의해 침투 깊이가 점차 깊어지고 끌림거리 8m 이후 침투깊이가 일정해지는 경향을 보였으며, 이는 끌림거리 8m 이후 해저케이블과 충돌해야 보수적인 설정임을 나타내고 있다. 이처럼 침투깊이가 일정해 지는 끌림 거리를 반영하여 앵커와 락범의 이격거리는 8m로 결정 하였다.
4. 락범 설계를 위한 해석
4.1 락범 단면 설계
앵커가 끌리면서 해저지반에 매설되어있는 케이블에 부딪히면 케이블은 끊어지며 파괴 된다.
이러한 위험을 방지하기 위한 보호공법으로 매설된 해저지반 상부에 락범을 시공하여 보강한다. 앵커가 체인과 함께 끌릴 때 락범 보강 효과에 의해 해저지반 내로 침투하지 않고 빠져나올 수 있으며, 락범 보강높이 변경에 따라 그 효과도 달라질 것이다. 따라서 락범 설계를 위해 먼저 유한요소 모델링은 사석으로 구성되는 락범의 경우 SPH(Smooth particle hydrodynamic) 기법과 DEM(Discrete element method)와 같은 개별적인 Particle로 모델링 하여 락범 거동을 구현할 수 있다. 하지만 현재까지의 상용 프로그램들은 CEL 기법과 위 두 모델링 기법 간의 연동이 불가능함에 따라 본 연구에서는 설계된 락범 보강 효과에 의한 앵커의 해저지반 침투깊이 영향을 평가하기 위해 락범을 해저지반과 같은 Eulerian으로 모델링 하였다. 설계 검증을 위한 락범 단면을 Fig. 9에 나타내었으며 적용된 물성치를 Table 2에 나타내었다. Fig. 9와 같이 락범 하단부 길이는 3절에서 결정된 앵커와 락범의 이격거리(8m)와 동일한 길이로 설정하였고, 상부 길이는 2m로 고정하였으며, 폭은 모델링된 해저지반의 폭과 맞추어 20m로 모델링 하였다. 또한 락범 높이를 3가지(0.5m, 1.0m, 1.5m)로 변경하며, 결정된 해석 시나리오에 따라 해저지반의 물성치 별 설계된 락범 단면 검증을 위한 앵커 끌림 시뮬레이션을 실시하였다.
4.2 락범 설계 단면 검증을 위한 앵커 끌림 해석
먼저 선행 연구로써 결정된 앵커 끌림 해석 시나리오를 Fig. 10에 나타내었다. 앵커와 락범의 이격거리 8m, 초기 앵커 침투 깊이는 Fluke 깊이(1.11m)만큼이며, 앵커 끌림 속도를 1.5m/s, 앵커 끌림 각도는 0°로 적용하였다. 여기서, 앵커와 락범의 이격거리는 끌림 시 앵커의 최하단부인 Fluke의 끝부분 Node point와 락범이 시작되는 부분 사이의 거리로 설정하였다. 또한 선행 연구와 동일하게 해석을 3단계로 설정하고, 3가지 해저지반 물성치(연약점토, 느슨한 모래, 조밀한 모래) 별 3가지 락범 타입(0.5m, 1.0m, 1.5m)에 따른 해석 case를 설정하였다.
실제 매설된 해저케이블 상부에 락범이 보강되며, 앵커 끌림시 매설된 해저케이블에 의한 해저지반이 끌림에 저항하는 힘 및 변형이 달라질 것으로 예상된다. 하지만 그 영향은 적을 것으로 판단되어 해저케이블의 모델링은 배제하고 락범으로 보강되는 정중앙부 아래 케이블이 매설되어 있다고 가정하였고, 설계된 락범 단면 검증을 위해 앵커 Fluke 끝부분 Node point의 궤적을 추적하여 락범 정 중앙부 하단에 앵커의 끌림에 의한 침투 깊이를 산정하였다.
5. 해석 결과 및 분석
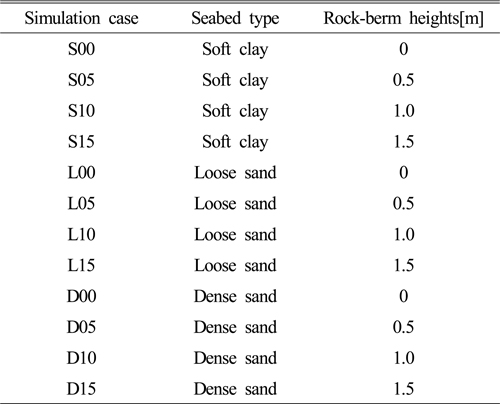
본 결과에서 해저지반 물성 종류와 락범 설계 단면에 따른 해석 Case를 Table 3과 같이 정의하였다. 정의된 해석 Case의 앞 대문자는 분류된 해저지반 물성치의 앞 대문자를 인용한 것 이며, 뒤 숫자는 설계된 락범 단면의 높이를 의미한다. 예를 들어 L10은 느슨한 모래의 해저지반에서 락범 높이 1.0m일 때의 해석 Case를 의미하고 대문자 뒤 00으로 설정된 Case는 락범이 보강되지 않은 Case이다.
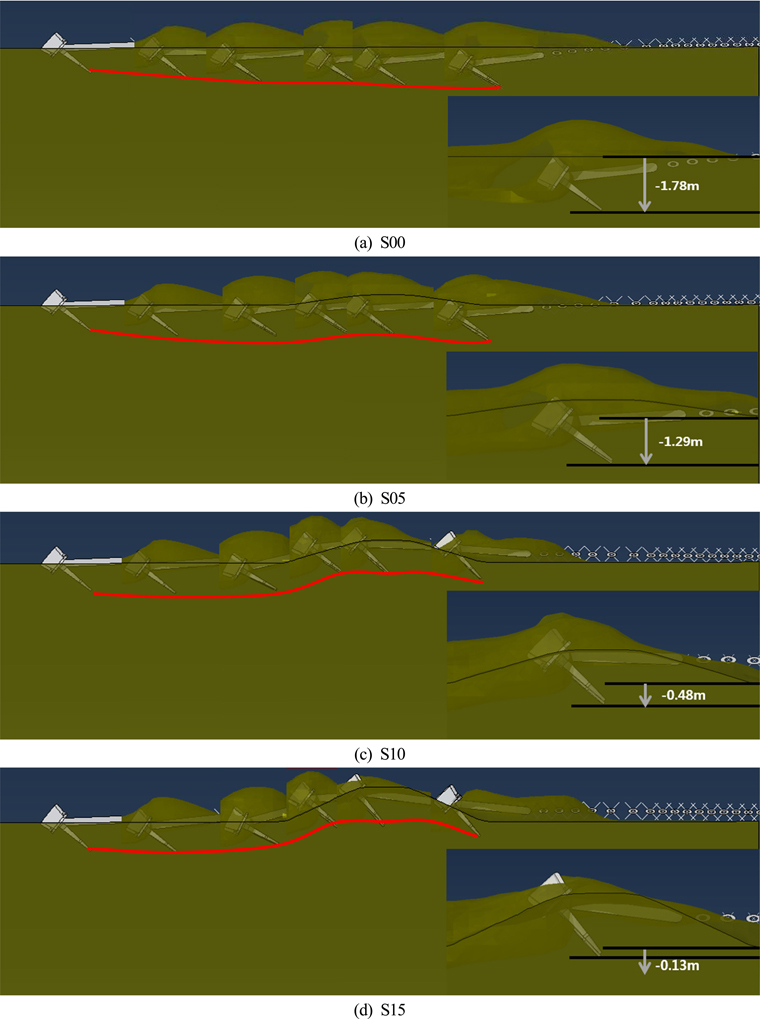
해저지반 물성이 연약점토에서의 락범 높이 변화(S05, S10, S15)에 따른 앵커 끌림에 의한 궤적과 락범 정 중앙에서의 침투 깊이에 대한 해석 결과를 Fig. 11에 나타내었다. 결과를 보면 해저지반 성질이 연약점토이고, 0.5m의 락범이 보강되었을 때, 락범 정 중앙에서의 앵커 침투깊이는 –1.29m로 해저면 기준 아래 (−)로 침투하는 결과를 보였으며, 락범의 보강 효과에 의해 앵커 끌림 시 침투하는 깊이가 점차적으로 줄어드는 것을 확인 할 수 있다. 하지만 설계된 락범 높이의 최대인 1.5m의 락범이 보강되어도 앵커가 침투하는 깊이는 해저면 기준 아래(−)값이 나타났으며, 이는 락범 정 중앙에 0.13m 이하로 매설된 케이블의 경우 앵커 끌림에 의해 충돌할 위험이 있다고 판단 할 수 있다. 또한 락범의 정 중앙을 지난 후 앵커가 끌림에 의해 해저지반에 재침투하는 결과를 보였으며, 이는 0°의 각도로 일정하게 끄는 보수적인 시나리오 설정에 의한 효과로 판단된다.
모든 Case에 대한 해석 결과를 Fig. 12와 같이 그래프로 나타내었다. 결과를 보면 설계된 락범 높이의 증가에 따른 앵커 침투깊이 감소율이 조성된 해저지반 물성 따라 차이를 보였으며, 연약점토는 약 52%, 느슨한 모래는 약 137%, 조밀한 모래는 약 126%씩 감소하는 결과를 보였다. 또한 단단하게 조성된 해저지반일수록 앵커가 침투하는 깊이에 대한 차이를 보였고 실제 느슨한 모래로 조성한 해저지반과 조밀한 모래로 조성한 해저지반에서 락범으로 보강 되지 않았을 때 앵커 침투깊이 결과가 –1.78m와 –0.439m로 75%정도의 차이를 보였다. 따라서 해저케이블이 묻혀있는 해저지반의 성질에 따라 락범 보강을 달리 적용해야 과다 설계 혹은 과소 설계를 방지할 수 있을 것이다.
6. 결 론
본 연구는 해저지반에 매설된 해저케이블을 앵커 끌림에 의한 충돌로부터 보호하기 위해 락범을 설계하고, 대변형 해석이 가능한 Abaqus/Explicit의 CEL기법을 적용한 수치 해석적 모형실험을 실시하였다.
앵커는 10.5ton 스톡리스 앵커를 선정하였으며, 끌림에 의한 락범 설계 검증 해석을 위해 다양한 변수들에 대한 시나리오 설정이 요구되었다. 이를 위해 Mohr-Coulomb 모델을 적용한 해저지반을 모델링 하여 락범으로 보강되지 않은 상태에서 초기 앵커 침투깊이, 앵커 끌림 속도 및 각도에 대한 변수들을 변경하며 앵커의 궤적을 추적하여 침투깊이를 산정하는 선행연구를 수행하였다. 그 결과 매우 보수적인 시나리오 설정을 위해 초기 앵커 침투깊이는 앵커 Fluke의 길이(1.11m)로 결정되었으며, 앵커의 끌림 속도는 1.5m/s, 각도는 0°로, 그리고 앵커와 락범의 이격거리는 8m로 결정 되었다.
다음으로 해저케이블을 보호하기 위한 락범 단면을 하단부 길이는 앵커와 락범의 이격거리인 8m, 상부 길이는 2m이며, 높이를 0.5m, 1.0m, 1.5m의 3가지 타입으로 설계 하였다. 또한 연약점토, 느슨한 모래, 조밀한 모래로 조성된 3가지 해저지반에서의 설계된 락범 단면을 검증 하는 해석을 수행하고, 락범 정 중앙에서의 앵커 침투깊이를 산정하여, 설계된 락범을 검증 하였다.
설계된 락범 검증 해석 결과 모든 해석 case에서 락범 적용에 의해 보강이 됨을 알 수 있었다. 또한 락범이 보강되지 않았을 때 연약점토로 조성된 해저지반과 조밀한 모래로 조성된 해저지반에서의 침투깊이 차이가 75%로 해저지반이 단단할수록 앵커 끌림에 의한 침투깊이가 감소하는 것을 알 수 있었다. 하지만, 연약점토에서는 설계된 락범의 최대 높이인 1.5m를 보강하여도 락범 정 중앙 에서의 앵커 침투깊이가 –0.13m로 해저지반 아래(−)로 침투하는 결과를 보였으며, 이는 해저케이블이 0.13m 이하로 매설된 경우 추가적인 락범 보강이 요구됨을 알 수 있었다. 또한 느슨한 모래로 조성된 해저지반의 경우 1.0m 높이로 설계된 락범 적용 시 락범 정 중앙에서의 앵커 침투깊이가 해저지반 +0.28m로 침투하지 않는 결과를 보였다. 이는 1.0m의 높이로 락범을 보강하면, 해저케이블의 매설된 깊이에 상관없이 충분히 안전하다고 판단할 수 있다. 마찬가지로 조밀한 모래로 조성된 해저지반의 경우 0.5m 높이로 설계된 락범 적용 시 안전한 결과가 나타났다.
따라서 연약점토에서는 1.5m 이상, 느슨한 모래에서는 1.0m, 조밀한 모래에서는 0.5m의 락범 높이를 적용해야 매설된 해저 케이블이 앵커 끌림에 의한 충돌로부터 안전하다고 판단 할 수 있다.
향후 앵커 끌림 실내실험에 의한 해저지반 침투깊이를 산정하고, 앵커 낙하에 의한 충돌 실내실험을 실시하여 락범 설계에 관한 앵커 낙하(Drop) 및 끌림(Drag)의 비교 연구를 진행할 예정이다.
Acknowledgements
본 연구는 2017년 산업통상자원부 지원 산업핵심기술과제 “ARC7 극지환경용 해양플랜트 내빙구조 설계기술 개발 (10063417)” 과제의 지원으로 수행된 결과임.
References
ABAQUS, 2017. ABAQUS User's Manual. ABAQUS 2017, Rhode Island, Dssault Systems.
ABAQUS User's Manual. ABAQUS 2017 Dssault Systems. Rhode Island: 2017.Das, B.M., 2009. Principles of Geotechnical Engineering. 7th Edition, Cengage Learning, USA.
Das B.M.. Principles of Geotechnical Engineering 7th Editionth ed. Cengage Learning. USA: 2009.Det Norske Veritas(DNV), 2010. Recommend and Practice DNV-RP-F107 Risk Assessment of Pipeline Protection. Norway, DNV
. Recommend and Practice DNV-RP-F107 Risk Assessment of Pipeline Protection DNV; Norway: 2010.Jung, J.J., Lee, Y.S., Shin, H.S., 2007. A Study for Construction of Shore-end Submarine Cable. Journal of The Korea Institute of Electronic Communication Sciences, 2(3), 203-209.
Jung J.J., Lee Y.S., Shin H.S.. A Study for Construction of Shore-end Submarine Cable. Journal of The Korea Institute of Electronic Communication Sciences 2007;2(3):203–209.Kim, Y.H., Jeong, S.S., 2014. Analysis of Dynamically Penetrating Anchor based on Coupled Eulerian-Lagrangian (CEL) Method. Journal of the Korean Society Civil Engineers, 34(3), 895-906.
Kim Y.H., Jeong S.S.. Analysis of Dynamically Penetrating Anchor based on Coupled Eulerian-Lagrangian (CEL) Method. Journal of the Korean Society Civil Engineers 2014;34(3):895–906. 10.12652/Ksce.2014.34.3.0895.Liu, Y., Hu, H., Zhang, D., 2013. Probability Analysis of Damage to Offshore Pipeline by Ship Factors. Jounal of the Transportation Research Board, 2326, 24-31.
Liu Y., Hu H., Zhang D.. Probability Analysis of Damage to Offshore Pipeline by Ship Factors. Jounal of the Transportation Research Board 2013;2326:24–31. 10.3141/2326-04.Qiu, G., Henke, S., Grabe, J., 2011. Application of a Coupled Eulerian-Lagrangian Approach on Geomechanical Problems Involving Large Deformations. Computers and Geotechnics, 38, 30-39.
Qiu G., Henke S., Grabe J.. Application of a Coupled Eulerian-Lagrangian Approach on Geomechanical Problems Involving Large Deformations. Computers and Geotechnics 2011;38:30–39. 10.1016/j.compgeo.2010.09.002.Shin, M.B., Seo, Y.K., 2017. Impact Characteristics of Subsea Pipeline Considering Seabed Properties and Burial Depth. Journal of Ocean Engineering and Technology, 31(3), 219-226.
Shin M.B., Seo Y.K.. Impact Characteristics of Subsea Pipeline Considering Seabed Properties and Burial Depth. Journal of Ocean Engineering and Technology 2017;31(3):219–226.SPS-KSA-V3311-5978, 2014. Anchor, Korea Industrial Standards.
Anchor Korea Industrial Standards; 2014. SPS-KSA-V3311-5978.Woo, J.H., Na, W.B., 2010. Analyses of the Maximum Response of Cylinders-Connected Protector under Anchor Colliding and Dragging. Journal of Ocean Engineering and Technology, 24(5), 81-87.
Woo J.H., Na W.B.. Analyses of the Maximum Response of Cylinders-Connected Protector under Anchor Colliding and Dragging. Journal of Ocean Engineering and Technology 2010;24(5):81–87.Woo, J.H., Na, W.B., Yu, J.S., 2014. Anchor Collision Simulation of Rock-berm using SPH Technique. Journal of Korean Society of Coastal and Ocean Engineers, 26(1), 9-15.
Woo J.H., Na W.B., Yu J.S.. Anchor Collision Simulation of Rock-berm using SPH Technique. Journal of Korean Society of Coastal and Ocean Engineers 2014;26(1):9–15. 10.9765/KSCOE.2014.26.1.9.Zhao, Y., Liu, H., 2015. The Drag Effects on the Penetration Behavior of Drag Anchors During Installation. Ocean Engineering, 109, 169-180.
Zhao Y., Liu H.. The Drag Effects on the Penetration Behavior of Drag Anchors During Installation. Ocean Engineering 2015;109:169–180. 10.1016/j.oceaneng.2015.09.011.