철근의 영향과 앵커 충돌각도를 고려한 유연콘크리트 매트리스의 손상평가
Damage Evaluation of Flexible Concrete Mattress Considering Steel Reinforcement Modeling and Collision Angle of Anchor
Article information
Abstract
A flexible concrete mattress (FCM) is a structural system for protecting submarine power or communication cables under various load types. To evaluate its of protection performance, a numerical analysis of an FCM under an anchor collision was performed. The explicit dynamics of the finite element analysis program ANSYS were used for the collision analysis. The influences of the steel reinforcement modeling and collision angle of the anchor on the collision behavior of the FCM were estimated. The FCM damage was evaluated based on the results of the numerical analysis considering the numerical modeling and collision environment.
1. 서 론
해저케이블은 전기공급과 통신망 구축을 위해 사용되며, 최근에는 해양풍력발전과 같은 녹색에너지 개발에서 송전설비로도 활용된다. 남해와 같이 양식이나 조업으로 선박 왕래가 잦은 해역에서는 해저케이블은 손상위험에 노출되어있다. 실제로 2006년 해남과 제주도간의 해저 케이블의 파손으로 인해 제주지역에 광역 정전 사태가 발생한 경우도 있었다. 해저케이블의 손상원인은 해양생물과 지형변화 등에 의한 해양환경적 요인과 조업도구나 선박 앵커에 의한 인위적 요인으로 구분되고, 이를 방지하기 위해 케이블 보호공법이 적용되고 있다(Woo, 2014). 이중 선박의 앵커 충돌이 가장 직접적이고 치명적인 원인으로 고려되고 있다. 케이블 보호공에는 케이블을 해저에 직접 매설하는 기본적인 방법과 구조물을 이용하는 방법이 있는데, 철근콘크리트 구조, 관형 구조, 망태형, 콘크리트 매트리스 등이 사용된다. 보호공의 형태로는 A-duct, U-duct, Rock-berm, Stone bag, 주철관, W-매트리스와 유연 매트리스 등이 있다(Ryu et al., 2015). Fig. 1은 케이블의 보호성능과 시공성 및 경제성이우수한 공법으로 평가되고 있는 유연매트리스 공법의 예를 나타낸 것이다.
해저케이블 보호구조물에 대한 성능평가를 위해서는 모형 및 실증시험과 수치해석적 방법이 가능하다. 케이블 보호공법에 대한 실증실험이 실행되어 성능평가가 수행되고 있으나(Yoon and Na, 2013), 이는 시간과 경제적 요인으로 다양한 손상조건에 대한 평가에 제약이 있다. 수치해석적 방법에 의한 케이블보호구조물의 손상평가는 일부 연구자들에 의해 수행되었다(Cho et al., 2012). Woo and Na(2010)는 원통연결 보호구조물에 대해 앵커충돌 및 끌림 해석을 수행하였고, Ahn et al.(2012)은 해양생물환경을 고려한 다양한 덕트형 구조물에 대해 안정성을 평가하였으며, Woo(2014)는 낙하하는 앵커의 항력계수 및 종단 속도 평가와 A-duct의 앵커 충돌해석에 대해 연구하였고, Ryu et al.(2015)은 유연매트리스 구조물에 대해 콘크리트 재료모델에 따른 거동 특성을 평가 하였다. Woo et al.(2015b)와 Woo et al.(2015c)는 Rock-berm 형태의 보호구조물에 대해 앵커충돌에 대한 동적특성을 파악하고 안정성해석을 수행하였다. 또한 Woo et al.(2015a)은 터널형태의 A-duct형 보호구조물의 앵커충돌 해석을 통해 손상을 평가하였다. 이와 같이 다양한 형상과 재료를 가지는 보호공이 시공되고 있지만, 보호공의 구조거동해석에 대한 기초자료가 부족하여 보호성능에 대한 평가가 필요하다.
따라서 본 논문에서는 보호성능이 우수한 유연 콘크리트 매트리스(Flexible concrete mattress, FCM) 보호공의 앵커 충돌해석에 대한 수치모델링과 충돌환경에 대한 손상거동 평가의 기초자료를 제시하고자 한다. 이를 위해 FCM 보호공의 손상분포에 철근의 모델링이 미치는 영향을 분석하고, 수중 낙하환경에 따라 변화할 수 있는 앵커의 충돌각도에 따른 보호공의 손상영향을 산정하고자 한다. 충돌해석에 사용된 프로그램은 ANSYS explicit dynamics이고 비선형 동적해석을 수행한다.
2. 수치해석 모델
2.1 FCM 모델링
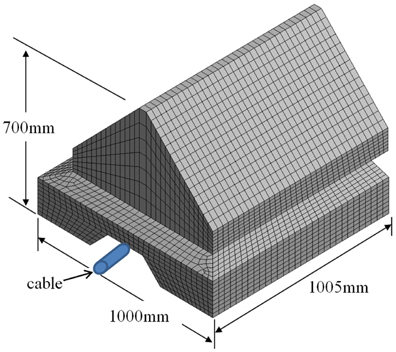
본 연구에서 대상으로 한 유연 매트리스 공법은 AS-FCM (Anchor resistant steel forced-FCM)으로 케이블 보호부분을 블록으로 보강한 형상이다(Fig. 1). AS-FCM은 케이블을 직접 보호하는 역할을 하는 중앙블록과 좌우의 날개 매트리스로 이루어져 있으며 중앙블록의 하부 홈에 케이블이 위치하고, 날개 매트리스 부분은 앵커 등의 끌림에 저항을 갖기 위해 배치된 것이다(New Technology of Electric Power, 2007). FCM 중앙블록 전체의 폭, 길이, 높이는 1,000mm, 1,005mm, 700mm이다.
앵커충돌의 손상을 방지하는 직접적인 역할을 하는 부분은 중앙블록이므로 본 연구에서는 이 부부만을 대상으로 Fig. 2와 같이 모델링을 하였다. 중앙블록의 유한요소모델은 절점 당 3개의 자유도를 가진 8절점 육면체 요소와 4절점 사면체 요소를 사용하여 구성하였다. 유한요소모델의 경계조건은 블록 하단면과 해저지반의 경계에 해당하는 절점의 자유도를 구속하여 설정하였다. 본 연구에서는 블록의 안정성만을 고려하므로 케이블은 모델링에서 제외하였다.
콘크리트 구조물의 충돌해석에 대한 대부분의 연구는 고속 접근하는 충돌체에 대한 것이고, 이와 관련하여 다양한 콘크리트 재료모델이 개발되었으나, 본 연구의 대상은 저속 충돌체에 대해 피충돌체의 안정성을 평가하는 것이다. Ryu et al.(2015)은 자유 낙하하는 앵커와 유연 매트리스 보호공의 해석에 있어서 콘크리트 재료를 탄성-완전소성, Drucker-Prager, RHT(Riedel-Hiermaier-Thoma)의 세 가지 모델로 해석을 수행하여 비교하였다. 해석결과 Riedel et al.(1999)과 Riedel et al.(2009)에 의해 개발된 RHT 모델이 콘크리트 케이블 보호공의 해석에서도 가장 적합하다고 나타났으며, 본 연구에서도 동일한 재료모델을 사용한다. RHT 콘크리트 모델에 사용되는 계수는 주로 정적재하 실험, 관통 실험, 폭발하중 실험 등의 다양한 실험에 의해 결정되는데 기존의 연구결과(Ryu et al., 2015)에 산정된 변수값을 사용하였고 Table 1과 같다.
2.2 앵커 모델링
충돌체는 선박용 앵커 중 하나인 스톡앵커(2.16ton)를 고려하였고, 한국표준협회(Korean Standards Association, KSA)의 규격을 바탕으로 유한요소 모델링을 수행하였다. 요소는 절점당 3개의 자유도를 가지는 4절점 사면체로 구성하였다. 강재 앵커는 콘크리트 보호구조물에 비해 강성이 매우 크고, 충돌 시 손상은 고려치 않으므로 강체로 취급하였다. 앵커의 유한요소 모델은 Fig. 3과 같다.
일반적으로 실증시험에서의 낙하높이는 10m이며, AS-FCM 현장낙하 시험에는 6m, 9m의 두 가지 케이스로 수행되었으며 (New Technology of Electric Power, 2007), 본 논문의 수치모델에서도 동일하게 적용하였다. Woo(2014)가 수행한 앵커충돌 시뮬레이션에서는 앵커의 수중에서의 종단속도를 이용하여 지상에서의 자유낙하 거리를 계산한 결과, 2ton의 스톡앵커와 스톡리스 앵커에 대해 각각 4.46m와 5.20m로 산정되었다. 따라서 낙하높이 6m와 1.5의 안전율을 고려한 9m는 비교적 합리적인 값이라고 생각된다. 실제 낙하높이를 수치해석으로 직접 구현할 경우에는 해석시간이 과도해지므로 콘크리트 보호공에서 50mm 떨어진 위치에서의 낙하속도로 모델링 하였다. 이를 위해 앵커의 운동에너지와 위치에너지의 총량이 보존된다는 조건으로 낙하속도를 계산하여 적용하였다(Ryu et al. 2015).
3. 철근 모델링에 대한 충돌해석 비교
3.1 철근 모델링
일반적으로 FCM은 철근 콘크리트 구조물로 제작된다. 수치 모델을 구성함에 있어 철근의 모델링이 충돌해석 결과에 미치는 영향을 계산하였다. 철근의 직경은 16mm로 가정하였고, 역학적 성질은 철근콘크리트 봉강의 산업규격(KS D3503)을 사용하였으며, 피복두께는 콘크리트 구조기준에 제시한 수중 콘크리트 규정을 적용하였다. 철근은 보요소를 사용했고 콘크리트와 완벽하게 부착된 것으로 가정하였다. 철근의 배치형상은 Fig. 4와 같다. 6m와 9m의 두 가지 낙하높이에 대해 각각 철근 모델링을 한 경우와 하지 않은 경우를 고려하여 4가지의 유한 요소모델을 구성하여 해석을 수행하였다. 즉, 철근을 고려하지 않은 모델은 무근콘크리트로, 철근을 배근한 구조물은 철근콘크리트로 모델링 하였다.
3.2 해석결과
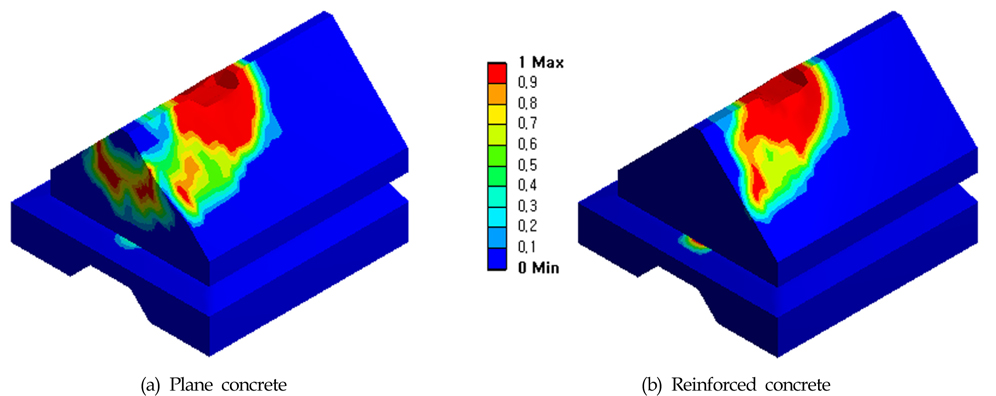
철근 모델링의 유무와 낙하높이에 따른 FCM 보호공의 충돌해석 결과로 손상 Contour를 Fig. 5~8에 나타내었다. 여기서, 손상은 RHT 재료모델에서 충격으로 인한 강도감소를 고려한 파괴변형률에 대한 소성변형률의 비로 계산되는 손상지수(Damage factor)를 나타낸다(Woo et al. 2015a).
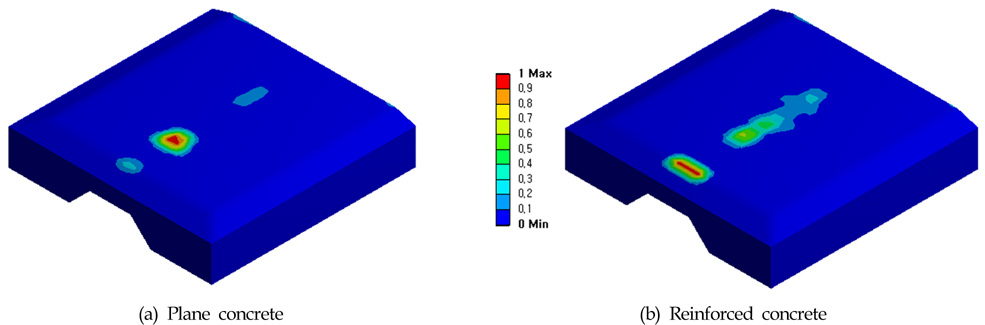
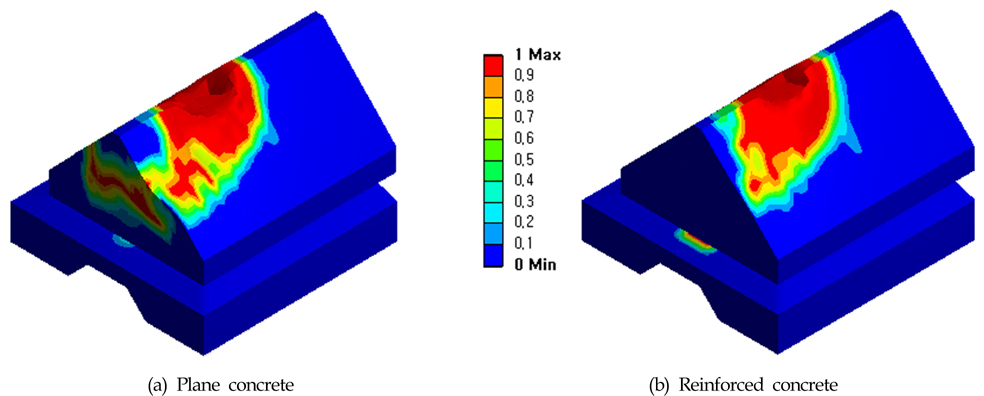
FCM 보호공을 상부블록과 하부블록으로 명칭하고, 전체구조물의 손상과 두 부분에 대한 손상을 구분하여 비교하였다. 초기 충돌부는 상부블록의 윗부분이지만, 충돌부에서 하부블록으로의 손상의 전달정도를 알아보기 위해 두 부분으로 구분하여 결과를 나타내었다. 즉, 케이블을 마지막으로 보호하는 부분은 하부블록이고, 하부블록이 파손되지 않는다면 케이블은 안전하므로 상부블록보다는 하부블록의 손상이 케이블에 직접적 영향을 준다고 고려한다. Fig. 5와 6은 상⋅하부블록으로 구성된 보호공 전체에 대한 결과이고, Fig. 7과 Fig. 8은 보호공의 하부블록에 대한 손상 결과이다.
해석결과에서 낙하높이가 클수록 충돌부에 발생한 크레이터는 더 크게 발생하여 손상면적이 증가하였음을 볼 수 있었다. Fig. 5와 Fig. 6에서 보면 무근 콘크리트에 비해 철근 콘크리트의 표면 손상부위가 전반적으로 감소하였고, Fig. 7과 Fig. 8에서는 하부 블록에서의 손상 패턴이 달라지는 것이 확인되었다. 이는 철근을 모델링하는 것이 상부블록의 강성변화로 나타나 하부블록에 미치는 영향이 달라지는 것으로 판단된다.
상부블록과 하부블록의 손상에 대한 정량적 분석을 위해, 손상이 발생한 절점의 수를 손상정도에 따라 Table 2에 나타내었다. 여기서, Case 1은 낙하높이 6m에 무근콘크리트인 경우이고, Case 2는 6m에 철근콘크리트, Case 3은 9m에 무근콘크리트, Case 4는 9m에 철근콘크리트인 경우이다. Table 2에서 보면 낙하높이가 클수록 상⋅하부 블록 모두에 대해 손상절점의 수가 증가하였다. 낙하높이 6m인 경우에 앵커가 직접 충돌되는 상부 블록에서는 철근 모델링의 영향으로 손상부위가 일부 감소하는 경향이 나타났고, 하부블록에서는 경우에는 철근을 모델링 함에 따라 손상정도가 큰 절점의 수가 발생하는 경향이 확인되었다. 낙하 높이 9m에서는 철근의 모델링 효과로 손상정도가 낮은 (0.5이하) 절점의 수는 대부분 증가하는 것이 나타났다. Fig. 9는 완전 손상(Damage=1.0)된 절점의 개수를 4가지 경우에 대해 비교한 것이다. Fig. 9에서 상부블록의 경우에는 철근의 모델링으로 인해 완전 손상된 절점의 수가 일부 감소하였지만, 하부 블록의 경우에는 완전손상된 절점의 수가 매우 작지만 오히려 증가하는 경향이 나타났다.
철근 모델링에 대한 결과를 보면 상부블록은 손상정도가 낮은 경우에는 철근을 모델링함에 따라 손상절점의 수가 증가 하였고, 손상정도가 높은 경우에는 전반적으로 손상 절점의 수가 감소하였다. 해석결과를 보면 유한요소 모델링 시에 철근을 고려함에 따라 FCM 보호공의 손상거동은 차이가 발생하며, 정밀한 충돌 해석을 위해서는 철근콘크리트 모델링이 필요하다고 판단된다.
4. 앵커 충돌 각도에 대한 영향
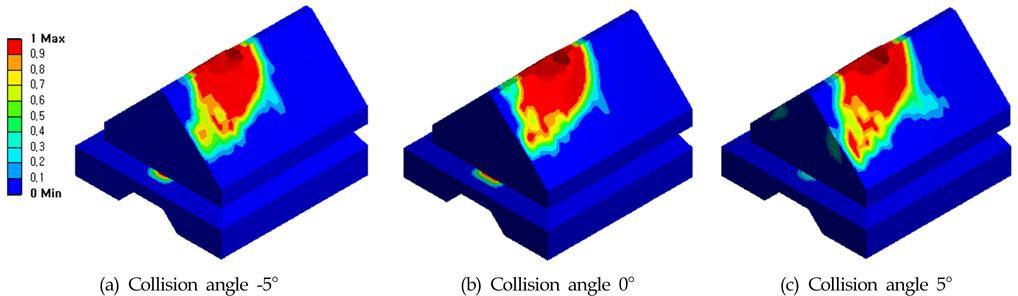
앵커는 해류와 조류 및 수심 등의 수중 낙하환경에 영향을 받아 경사를 가지고 충돌할 수 있다. 남해의 경우 해저 케이블이 주로 설치되는 지역에서의 최대유속을 고려했을 때, 스톡앵커의 최대 기울기는 약 5°정도로 산정된 바 있다(Woo, 2009). 앵커의 충돌 지점과 각도를 Fig. 10과 같이 -5°, 0°, 5°세 가지 경우에 대해 해석하였다. 충돌각도가 0°인 경우는 블록의 중앙으로 수직으로 낙하하는 경우이다. 낙하높이는 해류 및 조류의 영향이 상대적으로 큰 9m인 경우만을 고려하였다. FCM 보호공은 철근 콘크리트 모델로 유한요소모델을 구성하였다.
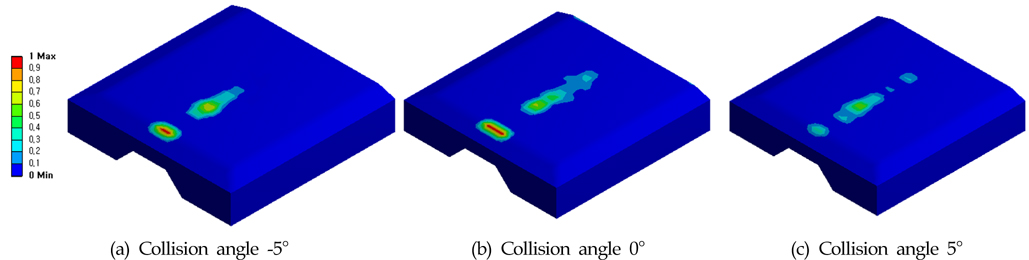
충돌해석 결과로 손상 Contour를 Fig. 11과 Fig. 12에 나타내었다. Fig. 11은 FCM 전체 블록에 대한 해석결과이고, Fig. 12는 하부블록의 결과이다. Fig. 11에서 보면 상부블록에 나타나는 크레이터의 크기는 충돌각도가 -5°, 0°, 5°로 갈수록 크게 나타났다. Fig. 12의 하부블록의 결과에는 분포양상이 충돌각도에 따라 일부 다르게 나타나는 것을 볼 수 있다.
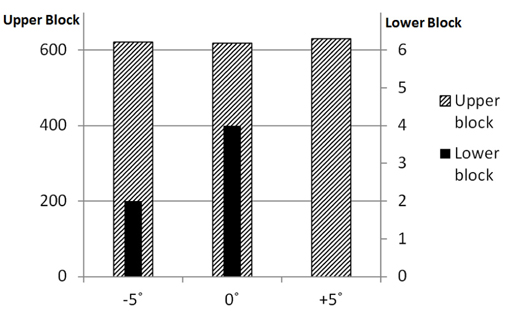
충돌각도에 따라 발생하는 손상절점의 수를 손상정도별로 Table 3에 나타냈다. 전반적인 손상절점의 수는 충돌각도가 5°인 경우가 가장 많고, 다음이 0°, -5°이다. 손상정도 높은 절점의 수는 상부블록의 경우 충돌각도가 5°인 경우가 가장 많았고, -5°인 경우가 가장 작았다. 하부블록의 경우에는 충돌각도가 0°경우에 손상정도가 높은 절점이 가장 많이 발생했다. Fig. 13은 상⋅하부 블록에 대해 완전 손상된 절점의 개수를 충돌각도별로 나타낸 것이다. 상부블록의 경우 5°에서 가장 많이 나타났으나, 세 가지 경우 모두에서 거의 유사하게 계산되었다. 하부 블록의 경우에는 충돌각도 5°에서는 완전손상된 절점이 계산되지 않았고, 충돌각도 0°인 경우에서 가장 많이 발생하였다. 해석결과를 종합해 보면 보호공 전체의 충돌손상은 경사낙하 하는 것이 가장 크게 발생하나 케이블위에 위치한 하부블록의 보호성능을 고려하면 낙하각도가 없이 수직낙하 하는 경우가 가장 치명적임을 나타냈다.
5. 결 론
본 논문에서는 해저케이블 보호구조물의 하나인 FCM에 선박용 앵커가 충돌하는 것에 대한 거동해석을 수치해석을 이용하여 수행하였다. 충돌해석 위해 유한요소해석 프로그램을 사용하였고 비선형 동적해석을 수행하였다. 충돌체인 앵커는 한국표준협회의 규격치수를 사용하여 강체로 모델링 하였고, 피충돌체인 FCM의 콘크리트 재료모델에는 RHT모델을 사용하였다. 유한요소모델을 구성함에 있어 철근의 모델여부가 충돌 해석결과에 미치는 영향을 두 가지 낙하 높이에 대해 분석하였다. 또한 해류나 조류 및 초기 낙하조건 등의 영향으로 발생하는 충돌각도의 변화에 대해 보호공의 충돌거동도 해석하였다. 앵커의 충돌각도는 -5°, 0°, 5°를 고려하였다. FCM을 초기 충돌부인 상부블록과 케이블 보호부인 하부블록으로 구분하여 충돌해석 결과를 분석하였고, 수치해석결과를 요약하면 다음과 같다.
(1) 낙하 높이가 클수록 충돌부위에 발생하는 크레이터는 크게 나타나며 손상면적도 증가하는 것이 확인되었다.
(2) 철근 콘크리트로 모델링한 경우가 무근 콘크리트로 한 경우보다 콘크리트 표면의 충돌 손상부위가 전반적으로 감소되었고, 상⋅하부 블록의 손상 패턴도 다르게 나타났다.
(3) 철근을 모델링할 경우에 상부블록에서는 손상정도가 작은 절점은 증가하였고, 낙하높이가 큰 9m인 경우에 하부블록에서는 손상절점이 전반적 증가하였다. 충돌 에너지가 큰 경우일수록 철근의 모델링이 필요하다는 것으로 판단된다.
(4) 앵커의 충돌각도에 대해 충돌부의 크레이터와 손상면적은 다르게 발생하였는데, 상부블록의 초기 충돌부에서는 크레이터가 충돌각도가 5°인 경우에 가장 크게 나타났고, 다음이 0°, -5°순이었다.
(5) 상부블록의 경우 완전 손상된 절점의 수가 충돌각도가 5°경우에 가장 많이 발생했으나, 세 가지 모두 유사하게 계산되었다. 하부블록은 충돌각도가 0°인 경우에 손상정도가 높은 절점이 가장 많이 발생했다.
FCM의 수치해석을 위한 유한요소 모델에는 배근된 철근의 모델링이 필요함이 확인되었다. 특히 케이블 보호부위인 하부 블록의 보호성능 평가에는 더 많은 영향을 미쳤다. 앵커충돌 각도는 FCM의 손상분포에 영향을 미쳤는데, 경사 낙하할 경우에 전반적인 손상부위는 증가하였지만, 구조물의 전체에서의 유의할 만한 손상과 하부블록에서의 완전손상을 고려한다면 수직 낙하하는 것이 보호성능에 가장 큰 영향을 미치는 경우라는 결론을 얻었다. 충돌해석에 대한 손상 분포특성과 손상 정도를 종합해 보면 보호구조물의 특성상 콘크리트 표면의 손상정도 보다는 보호대상 구조물의 보호성능에 초점을 맞추는 것이 필요하다고 생각된다.
Acknowledgements
이 논문은 부경대학교 자율창의학술연구비(2014년)에 의하여 연구되었음.
References
Ahn, S.H., Hue, H.K., Park, G.W., Hwang, S.B., Shim, W.I., 2012. Analysis of Echo-friendly Submarine Protection Duct. Proceedings of Joint Conference with Korean Association of Ocean Science and Technology Societies, Daegu Korea, 2383-2389.
Ahn S.H., Hue H.K., Park G.W., Hwang S.B., Shim W.I.. Analysis of Echo-friendly Submarine Protection Duct In : Proceedings of Joint Conference with Korean Association of Ocean Science and Technology Societies. Daegu Korea; 2012. p. 2383–2389.Cho, H.M., Kim, S.H., Ryu, Y.S., Kim, J.T., 2012. Numerical Simulation of Burial Submarine Cable Protector under Anchor Collision. Proceedings of Joint Conference with Korean Association of Ocean Science and Technology Societies, Daegu Korea, 1766-1770.
Cho H.M., Kim S.H., Ryu Y.S., Kim J.T.. Numerical Simulation of Burial Submarine Cable Protector under Anchor Collision In : Proceedings of Joint Conference with Korean Association of Ocean Science and Technology Societies. Daegu Korea; 2012. p. 1766–1770.New Technology of Electric Power, 2007. Assemble Type FCM(Flexcible Concrete Mattress) for Submarine Cable Protection. [Online] (Updated August 2007) Available at: <http://www.electricity.or.kr/> [Accessed Jan. 2016].
Assemble Type FCM(Flexcible Concrete Mattress) for Submarine Cable Protection 2007. [Online] (Updated August 2007) Available at: <http://www.electricity.or.kr/>. [Accessed Jan. 2016].Riedel, W., Kawai, N., Kondo, K., 2009. Numerical Assessment for Impact Strength Measurements in Concrete Materials. International Journal of Impact Engineering, 36, 283-293.
Riedel W., Kawai N., Kondo K.. Numerical Assessment for Impact Strength Measurements in Concrete Materials. International Journal of Impact Engineering 2009;36:283–293. 10.1016/j.ijimpeng.2007.12.012.Riedel, W., Thoma, K., Hiermaier, S., Schmolinske, E., 1999. Penetration of Reinforced Concrete by BETA-B-500 Numerical Analysis using a New Macroscopic Concrete Model for Hydrocodes. 9th International Symposium on the Interaction of the Effects of Munitions with Structures, Berlin-Strausberg, Germany, 315-322.
Riedel W., Thoma K., Hiermaier S., Schmolinske E.. Penetration of Reinforced Concrete by BETA-B-500 Numerical Analysis using a New Macroscopic Concrete Model for Hydrocodes In : 9th International Symposium on the Interaction of the Effects of Munitions with Structures. Berlin-Strausberg, Germany; 1999. p. 315–322.Ryu, Y.S., Cho, H.M., Kim, S.H., 2015. Collision Behavior Evaluation of Flexible Concrete mattress Depending on Material Models. Journal of Ocean Engineering and Technology, 29(1), 70-77.
Ryu Y.S., Cho H.M., Kim S.H.. Collision Behavior Evaluation of Flexible Concrete mattress Depending on Material Models. Journal of Ocean Engineering and Technology 2015;29(1):70–77. 10.5574/KSOE.2015.29.1.070.Woo, J., 2014. Behavior Characteristics of Submarine Power Cable Protectors under Anchor Collision. Doctoral dissertation, Pukyong National University.
Woo J.. Behavior Characteristics of Submarine Power Cable Protectors under Anchor Collision. Doctoral dissertation Pukyong National University; 2014.Woo, J., Na, W.B., 2010. Analysis of Maximum Response of Cylinders-connected Protector under Anchor Colliding and Dragging. Journal of Ocean Engineering and Technology, 24(5), 81-87.
Woo J., Na W.B.. Analysis of Maximum Response of Cylinders-connected Protector under Anchor Colliding and Dragging. Journal of Ocean Engineering and Technology 2010;24(5):81–87.Woo, J., Na, W.B., Kim H.T., 2009. Numerical Simulation of Arch-type Submarine Cable Protector under Anchor Collision. Journal of Ocean Engineering and Technology, 23(1), 96-103.
Woo J., Na W.B., Kim H.T.. Numerical Simulation of Arch-type Submarine Cable Protector under Anchor Collision. Journal of Ocean Engineering and Technology 2009;23(1):96–103.Woo, J., Kim, D., Na, W.B., 2015a. Damage Assessment of a Tunnel-type Structure to Protect Submarine Power Cables during Anchor Collisions. Marine Structures, 44, 19-42.
Woo J., Kim D., Na W.B.. Damage Assessment of a Tunnel-type Structure to Protect Submarine Power Cables during Anchor Collisions. Marine Structures 2015;44:19–42. 10.1016/j.marstruc.2015.07.005.Woo, J., Kim, D., Na, W.B., 2015b. Application of Numerical Simulation of Submersed Rock-berm Structure Under Anchor Collision for Structural Health Monitoring of Submarine Power Cables. Smart Structures and Systems, 15(2), 299-314.
Woo J., Kim D., Na W.B.. Application of Numerical Simulation of Submersed Rock-berm Structure Under Anchor Collision for Structural Health Monitoring of Submarine Power Cables. Smart Structures and Systems 2015;15(2):299–314. 10.12989/sss.2015.15.2.299.Woo, J., Kim, D., Na, W.B., 2015c. Safety Analysis of Rock-berms that Protect Submarine Power Cables in the Event of an Anchor Collision. Ocean Engineering, 107, 204-211.
Woo J., Kim D., Na W.B.. Safety Analysis of Rock-berms that Protect Submarine Power Cables in the Event of an Anchor Collision. Ocean Engineering 2015;107:204–211. 10.1016/j.oceaneng.2015.07.057.Yoon, H.S., Na, W.B., 2013. Anchor Drop Tests for a Submarine Power-cable Protector. Marine Technology Society Journal, 47(3), 72-80.
Yoon H.S., Na W.B.. Anchor Drop Tests for a Submarine Power-cable Protector. Marine Technology Society Journal 2013;47(3):72–80.