다양한 수직방향 무게중심을 고려한 사항 중 탱커 선체에 작용하는 유체력에 관한 연구
Study on Hydrodynamic Forces Acting on Tanker Hull with Consideration of Various Vertical Centers of Gravity in Drift Test
Article information
Trans Abstract
An investigation was conducted to determine whether the changes in the maneuvering forces and moments acting on a hull could be affected by changing the vertical center of gravity (VCG) of a tanker. The changes in the hydrodynamic forces and moment acting on a hull according to the restraint conditions of motion were examined using CFD for cases where the VCG was located at the design draught (100% of draught), under the design draught (75% of draught), and at half of the design draught (50% of draught). The following motion restraint conditions were selected: (1) fixed restraints for everything; (2) heave, pitch, and roll free restraint; and (3) heave and pitch free restraints. It was found that restraint condition (2) had the best agreement with the model experiment results. In addition, it was found that the hydrodynamic forces and moment acting on the hull with restraint condition (2) could be greatly affected in the model tests and CFD calculations by the various configurations for the vertical center of gravity of the hull. Finally, it was concluded that the location of the vertical center of gravity of the hull could be an important factor when more accurate hydrodynamic maneuvering forces and moment are estimated.
1. 서 론
최근 조선 산업에서 부상하고 있는 탄소배출량 규제 등의 친환경적인 이슈들은 에너지효율 설계지수(EEDI, Energy efficiency design index) 규제와 관련된 사항들이 저항 추진분야 뿐만 아니라 조종성 분야에서도 대두되고 있는 실정이다. 따라서 EEDI에 관련된 제약 사항을 만족시키기 위해서 각 조선소에서는 성능 향상을 위한 연구에 집중하고 있는 추세이다. 이러한 가운데 국제해사기구(IMO, Interantional Maritime Organization) 산하의 해양환경보호위원회(MEPC, Marine Environment Protection Committee)는 기술력의 뒷받침이 되지 않는 일부 조선소에서 EEDI에 대한 규제를 만족시키기 위해 선박의 엔진 성능 등을 낮추어 선박을 건조하여 선박의 조종성능을 저하시킬 수 있다는 점을 우려하여 2013년에는 황천 중 조종성능에 관한 조항을 만들 것을 제안하였다(MEPC.232(65))(IMO, 2013). 따라서, 유럽에서는 SHOPERA (Ship operation) 프로젝트를 발족하여 지속적으로 이와 관련된 연구를 수행했으며, 국내에서도 이에 대한 연구를 수행하고 있는 실정이다.
한편, 선박의 조종성능에 대한 연구는 과거 20년간 많은 연구기관에 의해 모형시험, 수학모델 연구 및 이론해석 등 다양한 방법으로 수행되어 왔으며 최근에는 IT분야의 비약적 발전 및 보급으로 인해 선박의 초기 설계단계에서 조종성능 추정에 활용할 목적으로 Computational fluid dynamics(CFD)의 활용이 적극적으로 시도되어 왔다. 초기의 CFD를 활용한 연구에서는 주로 사항 중 선체에 작용하는 유체력에 관한 정확도 향상을 목적으로 난류모델, 격자크기 및 자유수면의 유무에 따른 영향을 살펴보는 연구를 주로 수행하여 구속모형 시험 결과와 비교하였다. Toxopeus(2011)는 그의 연구에서 선형별, 격자별 사항 및 선회시 선체에 작용하는 횡력 및 선회모멘트를 CFD를 사용하여 계산한 후 구속모형시험 결과와 비교하였다. Toxopeus(2011)의 연구에서는 자유수면의 효과와 선체의 자세변화는 고려되지 않았다. Toxopeus(2011)의 연구에서 비교대상이 된 선체인 HTC (Hamburg test case) 및 KVLCC(KRISO very large crude-oil carrier)2는 각각 HSVA(Hamburgische Schiffbau-Versuchsanstalt) 및 INSEAN(Istituto Nazionale di Studied Esperienze di Architettura Navale)에서 구속모형시험을 실시하였으며, HTC의 경우는 6자유도(Degree of freedom, DOF) 방향 모두 구속되어 모형시험이 수행되었다. 또한, KVLCC2의 경우 종동요(pitch) 및 상하동요(heave)를 제외한 운동에 대해 구속이 이루어진 상태로 모형시험이 수행되었다. 하지만, Toxopeus(2011)는 KVLCC2에 대한 CFD 계산에서 자유수면 및 자세변화를 고려하지 않았으며, INSEAN에서 수행된 구속모형시험에 대한 상세한 정보 또한 공개되지 않아 계산 및 모형시험이 동일한 조건으로 고려되었는지는 정확히 밝혀진 바가 없다. 또한, Toxopeus et al.(2013)는 다양한 점성유동 해석자(REFRESCO, Star-CCM+, ISIS-CFD 및 CFDShip-Iwoa)를 이용하여 KVLCC2의 제한된 수역(협수로 및 천수역)에서 조종운동하는 선체에 작용하는 유체력 추정에 대한 다양한 검토(자유수면의 유무, 종동요 및 상하동요의 구속여부)를 수행하였다. 비교 계산 조건으로는 모형시험을 포함하여 다양한 결과가 존재하는 사항각 4도를 선정하였으며, 각각의 해석자의 결과를 모형시험과 비교 분석하였다. 그의 연구결과에 따르면 자유수면의 유무 및 운동의 구속여부를 점성유동 해석에서 고려하는 지의 여부에 따라 결과의 정확도가 달라질 수 있음을 보였다. 그의 연구에서 주목해야할 내용 중의 하나는 유동해석의 결과와 모형시험 결과를 비교할 때, 상호간의 조건의 차이가 결과에 영향을 미칠 수 있음을 보였다. 이는 Sung and Park(2015)의 계산에서도 확인되는 사항으로 Sung and Park (2015)의 연구에서는 대각도 사항 시에도 모형시험과 비교적 잘 일치함을 보여주고 있으며 조종유체력에 대한 점성유동 계산 시 횡동요 및 상하동요의 구속 여부가 계산의 정확도에 영향을 미칠 수 있음을 보여주고 있다고 판단된다.
일반적으로 점성유동 계산을 수행하고 모형시험과 비교를 수행할 때 계산과 모형시험이 동일한 조건에서 수행되지 않거나, 비교를 위해 참고하는 정보가 정확하지 않기 때문에 발생할 수 있는 오차에 대한 검토가 면밀히 검토되지 않을 수 있다고 판단된다. 이러한 사항은 모형시험을 수행하는 기관 또는 연구자와 점성유동 계산을 수행하는 기관 또는 연구자가 다르거나 비교를 위한 선택된 모형시험 결과가 계산보다 선행되는 경우가 일반적이기 때문에 빈번히 일어 날 수 있다고 판단된다. 특히, 조종유체력 획득을 위해 수행 되는 구속모형시험의 경우 수행기관에 따라 모형시험 조건이 달라질 수 있을 것이며 이에 대한 충분한 정보가 공개되지 않기 때문이라고 말 할 수 있을 것이다.
따라서, 본 연구에서는 상기에서 언급한 내용들에 주목하여 사항운동 중 횡방향 동요에 대해서 수직방향 무게중심의 변화가 조종유체력의 변화에 미치는 영향에 대한 검토를 점성유동 계산을 통해 수행하였다. 모형시험에 대한 비교적 정확한 정보 획득을 위해 Sung and Park(2015)의 연구에서 검토된 KVLCC1 및 KVLCC2 중 KVLCC1를 비교 대상선으로 선택하였으며, KVLCC1의 수직방향 무게중심(Vertical center of gravity, VCG)을 임의로 변경 했을 때 선체에 작용하는 유체력의 변화를 살펴보았다.
2. 수치해석 방법
점성유동 해석을 위한 지배방정식은 비압축성 난류 유동에 대한 지배방정식인 연속방정식과 Reynolds averaged Navier-Stokes (RANS) 방정식이다. 본 연구에서 사용된 CFD 해석자는 Open-source tool-kit인 OpenFOAM(Open-source field operation and manipulation, 이하 오픈폼)을 사용하였다. 오픈폼에서 사용되는 수치계산방법은 운동량 및 질량에 대한 보존법칙을 만족시키기에 용이하도록 적분하여 기초방정식을 이산화하는 방법인 유한체적법을 사용한다. 계산에 사용된 난류모델은 k-ω SST(Shear stress transport)이고, 시간항에 대해서는 1차 정확도의 암시적(Implicit) Euler기법을 사용하였다. 공간항에 대해서는 대류항의 경우는 2차정확도인 LinearUpwind를 적용하였고, 확산항의 경우는 2자 정확도인 중심 차분법을 적용하였다. 자유수면은 VOF(Volume of fluid) 기법을 활용하였다.
2.1 대상 선박
계산에 사용된 선박은 선박해양플랜트 연구소의 공개 선형인 KVLCC1을 사용하였다. 축척비는 Sung and Park(2015)의 연구에서 수행된 모형시험에 사용된 1/46.426이며, 주요 제원은 아래 Table 1을 통해 확인해볼 수 있다. Table 1에서 Lpp는 해당흘수에서의 수선간장길이, B는 선박의 폭, T는 흘수를 의미한다.
2.2 격자 시스템
계산에 사용된 대상선은 KVLCC1으로 최근 SIMMAN(2008)을 통해 많은 비교 데이터가 공개되었고, Sung and Park(2015)에 의해 재현 연구가 발표되었기 때문에 본 연구에서도 대상선으로 채택하였다. 격자생성에 사용된 소프트웨어는 Trimmer 형태의 격자를 생성하는데 용이한 NUMECA사의 Hexpress를 사용하였다. Hexpress는 계산 대상의 관심 있는 표면을 세분화하여 격자를 생성할 수 있다는 장점을 가지고 있으며, 비교적 우수한 질의 격자를 생성할 수 있다. 계산 영역의 설정은 선체 길이를 단위로 설정하여 대상 선박이 변경되더라도 비슷한 격자 생성이 되도록 하였다. 각 경계층의 설정은 유동이 선박에 반사되어 발생할 반사파로 인하여 실제 계산에 정확성을 감소시키는 것을 막고자 유동의 선미부로부터 출구경계까지 1.5Lpp, 선수로부터 유동의 입구경계까지 0.8Lpp, 각 선측면으로는 선체 중심 기준 1.5Lpp, 선체 중심 기준으로부터 수저경계까지 1.5Lpp, 상층경계까지는 0.5Lpp로 설정하였다. 전체 격자 개수는 계산 시간과 직결되기 때문에 유동장이 급격하게 변하는 선체 주위는 미소하게 격자를 구성하고 상대적으로 유동장의 변화가 적은 경계층 부근은 크게 설정하는 Trimmer 격자 기법을 활용하였다. 또한, 선체의 움직임을 고려하였을 때 횡동요와 종동요의 연성으로 인해 선체의 상하 방향으로의 변위가 상대적으로 크게 발생하여 자유 수면의 VOF 기법을 적용하는 데에 무리가 있음을 인지하여 자유 수면 부근의 격자를 좀 더 미소하게 생성하였다. 추가적으로 선체 표면의 유동을 좀 더 정확하게 계산할 수 있도록 경계층 격자(Prism layer)기법을 사용하여 선체 표면으로부터 5~7개의 격자 층을 적용하였다. 그 결과 최종적으로 230만개의 격자로 구성하였다. 작성된 전체 도메인의 형상은 Fig. 1을 통해 확인할 수 있다. Fig. 1로부터 도메인의 좌표계는 선수에서 선미방향을 양(+)의 x, 선수를 바라볼 때 우측을 양의 y 및 연직 상방향을 양의 z로 정의된다.
3. 수치해석 결과
3.1 이산화 기법 및 시간 간격 결정
본 연구에서는 CFD 계산에 있어 계산의 정확도 및 효율성을 위하여 대류항의 이산화 기법 및 시간간격의 변화가 조종 유체력에 끼치는 영향을 살펴보았다. 가장 효율적인 이산화 기법과 시간 간격을 선정하기 위하여 Table 2에 나타난 바와 같은 조건으로 계산을 수행하였다. 주어진 계산 조건에서 3자유도 운동(상하동요, 종동요 및 횡동요)에서 유체력에 대한 차이를 확인하기 위하여 비교적 대각도 사항각인 20도로 설정하였다. 사항각은 선체를 고정시킨 상태에서 유동의 방향을 원하는 각도만큼 벡터로 표현하여 고려하였다. 한편, Table 2에서 Types 및 Variable에 표기된 fvScheme(Finite volume scheme), LinearUpwind(Linear upwind), interfaceCompression(Interface compression), limited Grad(Limited gradient) 등은 전산유체역학에서 사용되는 용어들을 오픈폼에서 사용하기 위하여 생성된 표기법으로 일종의 변수명이라고 생각하면 이해에 도움이 되리라 판단된다.
3.1.1 대류항 이산화 기법별 조종 유체력 계산 및 결과비교
본 연구에서는 수직방향 무게중심의 변화에 따른 조종 유체력의 변화에 대한 검토를 수행하기 전에 VOF 및 운동량방정식에 존재하는 대류항에 대한 이산화 기법별 해석의 정확도를 살펴보았다. Figs. 2-5는 VOF 및 운동량방정식의 대류항을 이산화한 기법에 따른 계산결과 및 모형시험과의 비교를 보여주고 있다. Fig. 2 및 Fig. 3의 결과에 따르면 VOF 방정식의 대류항을 2차 정확도의 LinearUpwind limitedGrad 기법을 사용했을 때 사항각 20도에서의 선체에 작용하는 횡력 및 모멘트가 비교적 모형시험 결과와 차이가 작음을 알 수 있다. 또한, Fig. 4 및 Fig. 5로부터 2차 정확도인 Gauss linear 기법이 가장 좋은 결과를 산출함을 알 수 있다. 하지만, 본 연구에는 기재하지 않았지만 다른 사항각도에 대해서도 계산을 수행한 결과 Gauss linear 기법은 상황에 따라서 불안정한 거동을 보였기 때문에 모든 사항각에서 안정성 및 정확도를 보인 2차 정확도의 LinearUpwind limitedGrad 기법을 추후 계산에서 적용하도록 결정하였다.
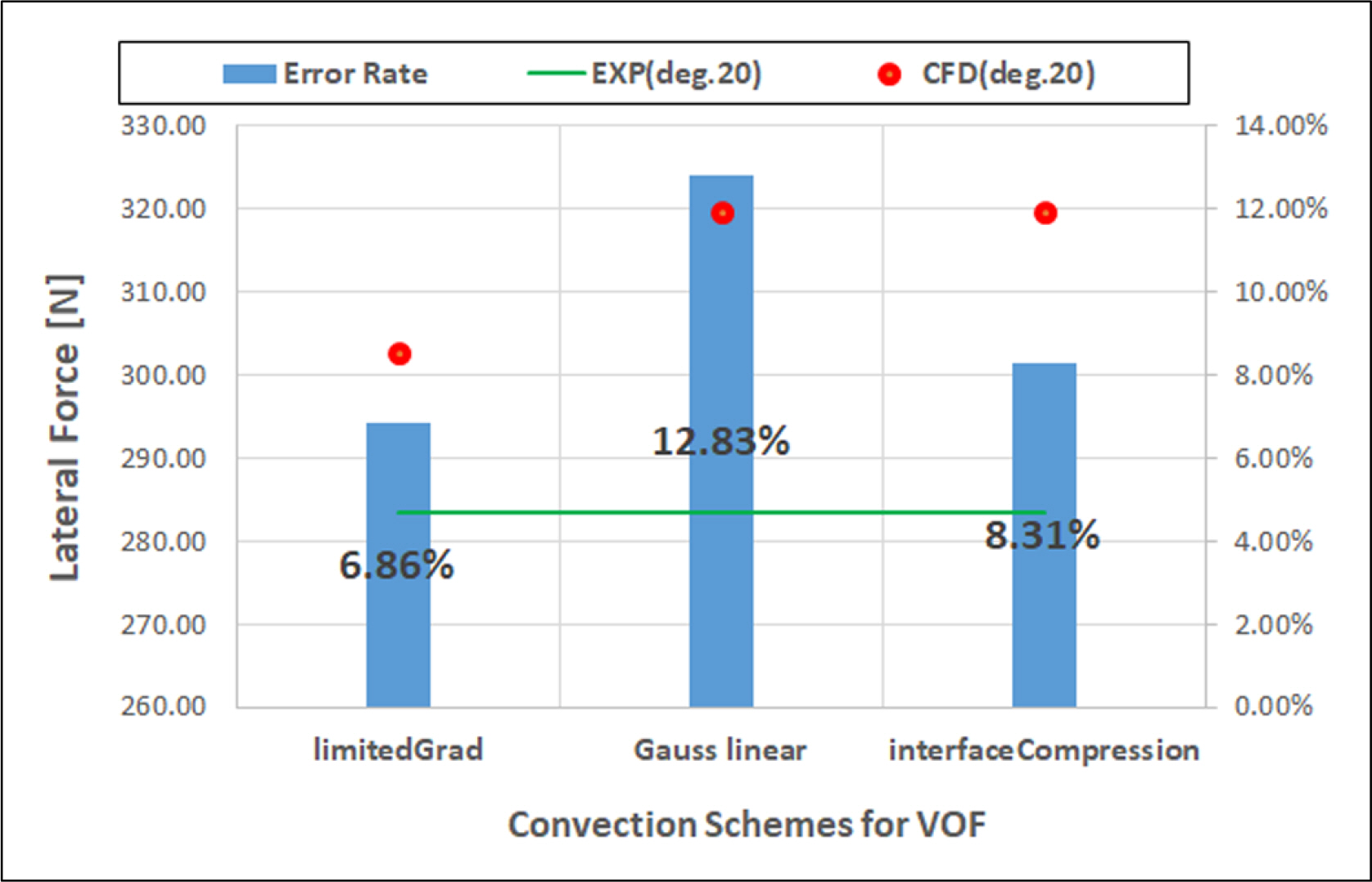
Comparison results between experiment and calculation in lateral forces with different convection scheme of VOF

Comparison results between experiment and calculation in yaw moment with different convection scheme of VOF
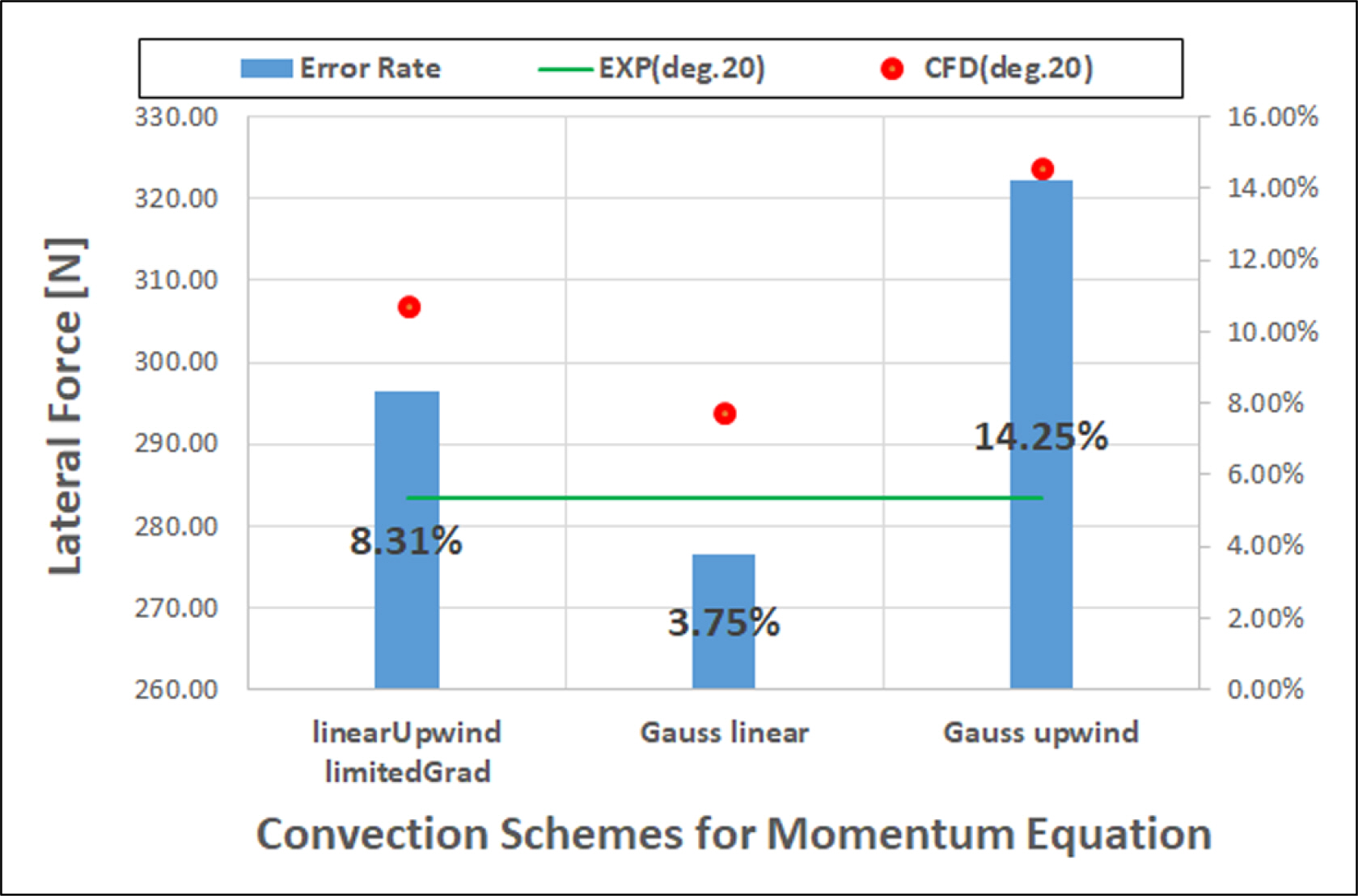
Comparison results between experiment and calculation in lateral forces with different convection scheme of momentum equation
3.1.2 시간 간격별 조종 유체력 계산 및 결과비교
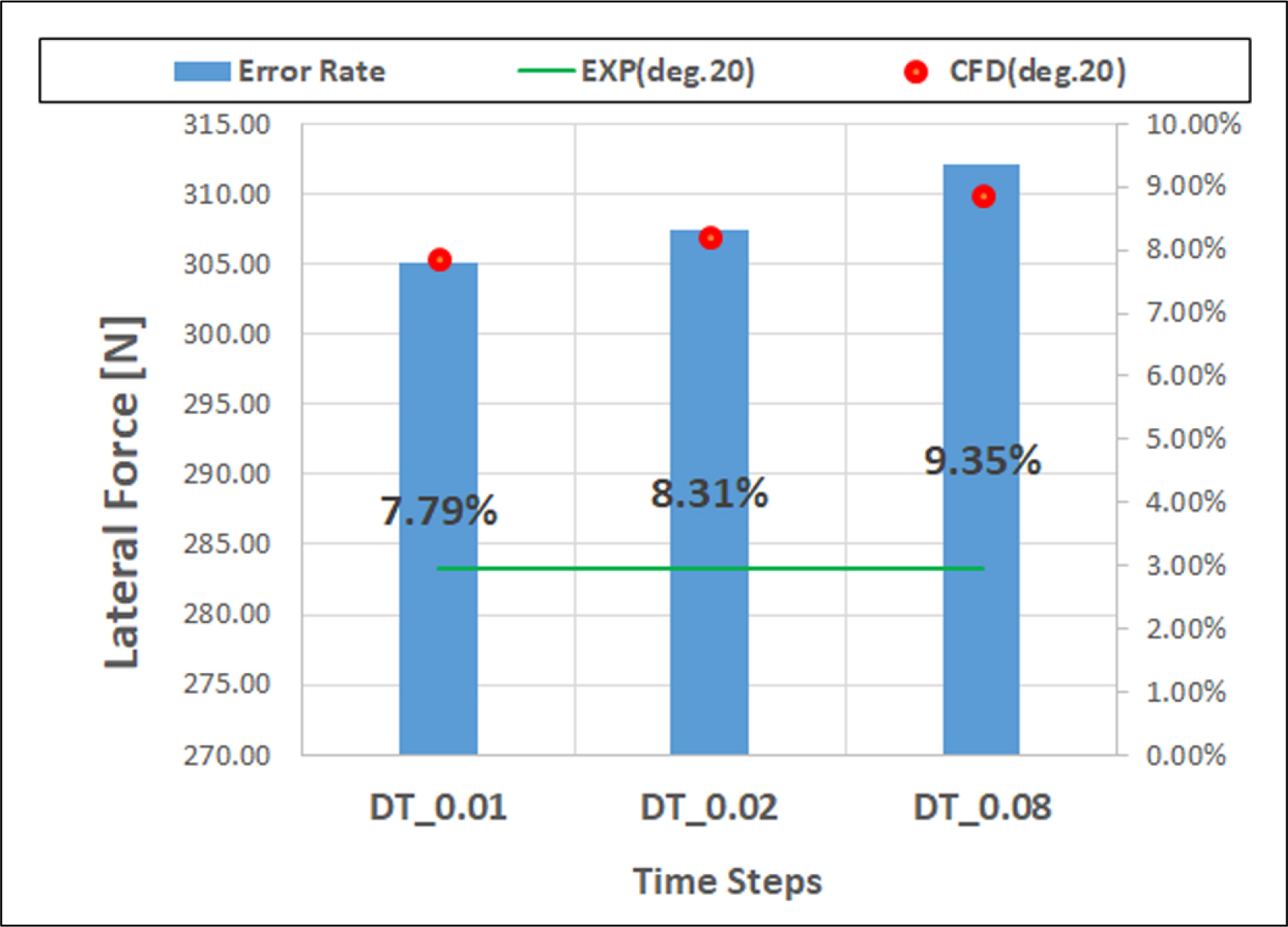
본 연구에서는 선체의 사항중 선체의 3자유도 계산을 무게중심의 변화별로 검토를 수행하기 때문에 계산의 정확도 보다는 안정성이 중요할 것으로 판단되어 시간항의 이산화 기법으로 1차 정확도의 암시적 Euler법을 사용하였다. 또한, 계산결과의 수렴성 확인 및 계산의 효율성을 살펴보기 위해 시간 간격별 유체력 계산을 수행한 후 앞 절과 마찬가지로 모형시험 결과와 비교하였다.
Fig. 6과 Fig. 7로부터 알 수 있듯이 시간 간격이 줄어들 수 록 계산의 결과와 모형시험과의 차이가 줄어드는 경향을 보인다. 하지만, 시간 간격이 0.01인 경우 계산양의 증가가 불가피 함으로 계산양의 효율성을 고려하여 본 연구에서는 시간 간격을 0.02로 설정하여 추후 계산을 수행하였다.
3.2 수직방향 무게중심의 위치 변화별 조종 유체력 계산 및 결과비교
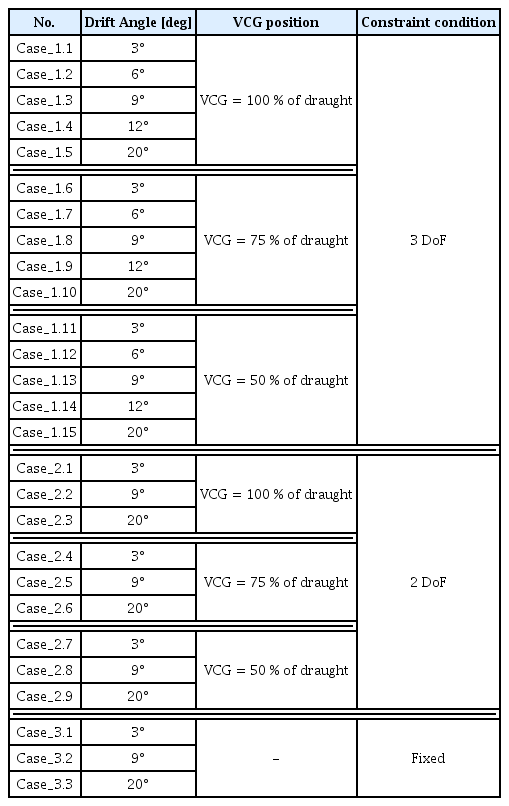
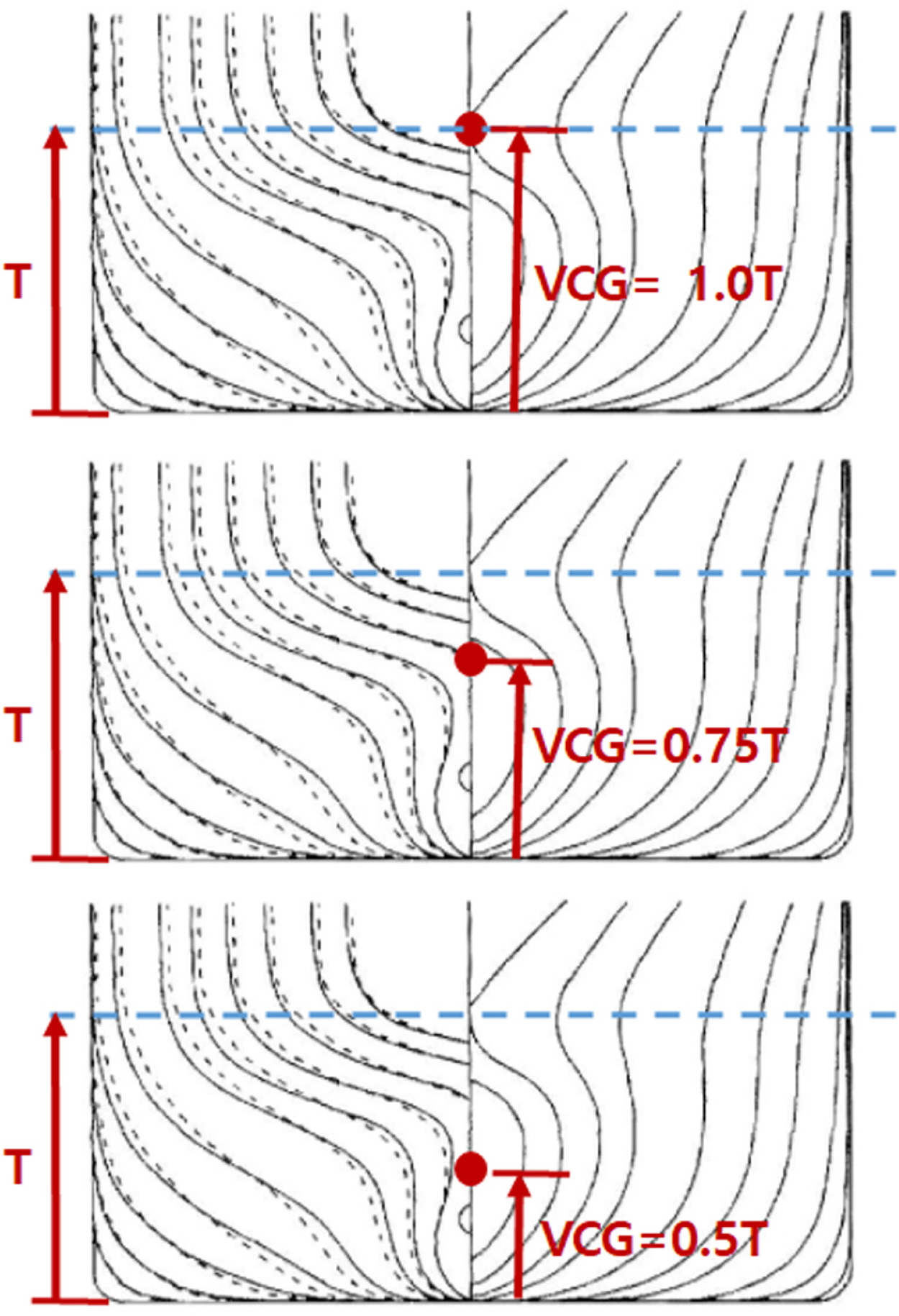
수직방향 무게중심의 위치 변화별 조종 유체력의 변화를 살펴보기 위하여 검토는 크게 (1) 사항각, (2) 수직방향 무게중심의 위치 변화 및 (3) 구속 조건 변화의 3가지로 구분되며, 각각의 조건에 따른 계산 매트릭스를 구성하였다. Table 3에서 확인할 수 있듯이 사항각은 소각도인 3도부터 대각도인 20도까지 Sung and Park(2015)에서 수행된 사항시험을 기준으로 설정하였다. Sung and Park(2015)은 명시적으로 모형시험의 구속조건 및 VCG에 대한 정보를 명시하지 않았지만, KVLCC 선형에 대한 모형시험 시 상하동요, 종동요 및 횡동요에 대해 구속을 하지 않은 조건으로 모형시험을 수행하였다고 판단된다. 또한, 모형선의 무게 중심은 SIMMAN(2008)에서 명시된 횡동요 고유주기 및 GM(Metacentric height)을 이용하여 모형선의 수직방향 무게중심을 결정하였다고 판단된다. 따라서, 본 연구에서 대상선으로 선택된 KVLCC1의 경우 탱커선으로 수직방향 무게중심이 상부 갑판을 기준으로 연직 하방향으로 분포하고 있다고 가정하여, Fig. 8에 나타낸 바와 같이 선저로부터 설계흘수까지의 거리를 기준으로 하여 흘수의 100%, 75% 및 50% 3가지의 위치에 수직방향 무게중심이 분포하는 것으로 상정하여 무게중심의 위치변화를 고려하였다.
끝으로 운동의 구속 조건은 실험 조건인 횡방향동요(Roll), 상하방향동요(Heave) 및 종동요(Pitch)의 3방향의 운동 구속을 해제한 운동(3DoF, Degree of freedom)과 선수동요(Pitch)와 상항동요(Heave)의 2방향의 운동만을 구속 해제한 2자유도(2DoF) 운동 그리고 모든 방향으로의 운동을 구속(Fixed)한 경우의 3가지 조건에 대해 선체에 작용하는 조종 유체력의 차이를 살펴보았다. 모든 계산의 결과는 주기적으로 변하면서 수렴을 하기 때문에 계산이 수렴하는 구간을 기준으로 3주기 값의 평균값을 최종 결과 값으로 선택하였다. 계산 종료 시간은 60초로 제한하였는데 이는 계산의 효율을 고려하기 위함이었으며, 힘의 시계열 값을 확인하면서 계산을 수행하여 계산의 수렴을 고려하였다.
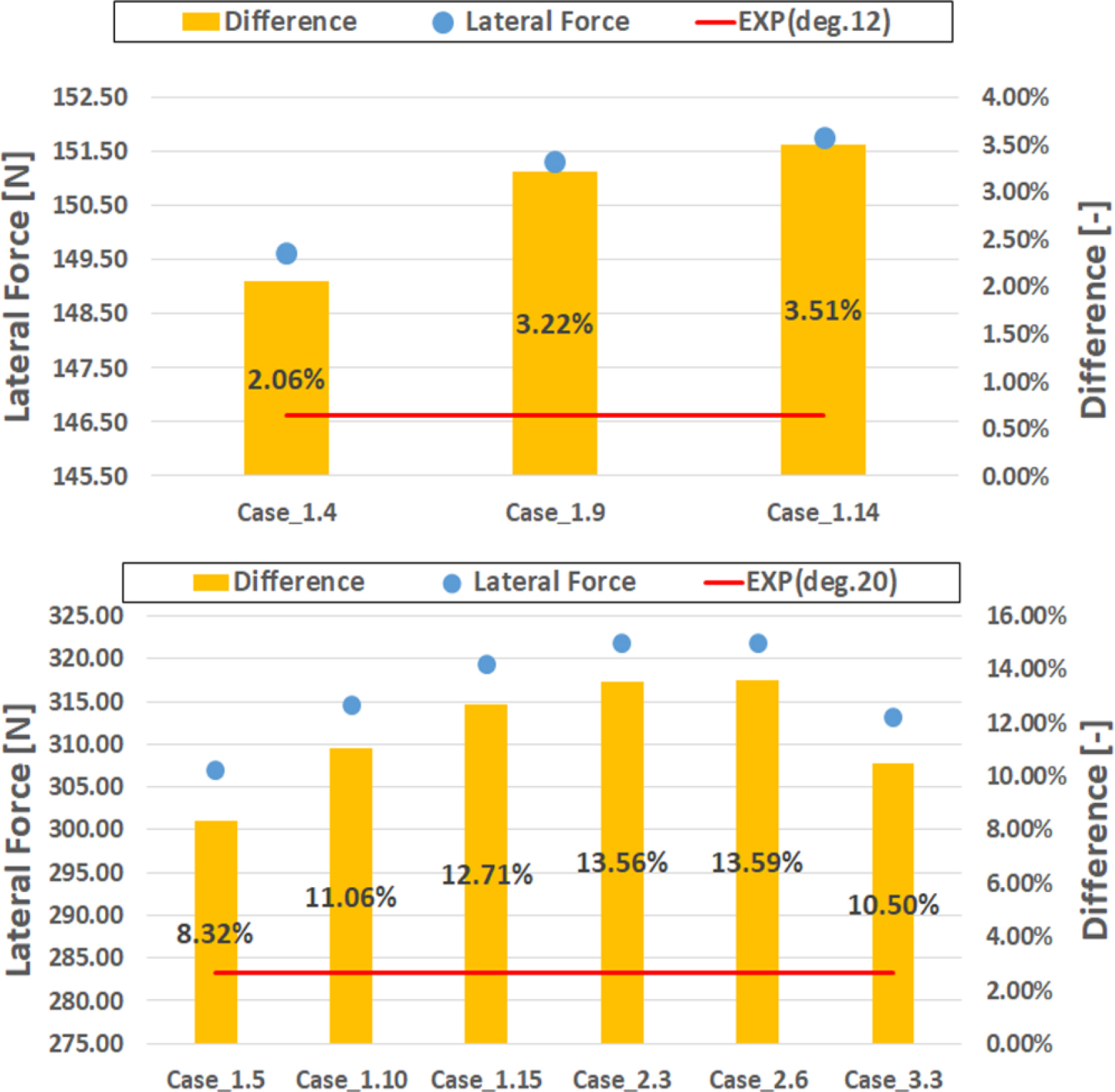
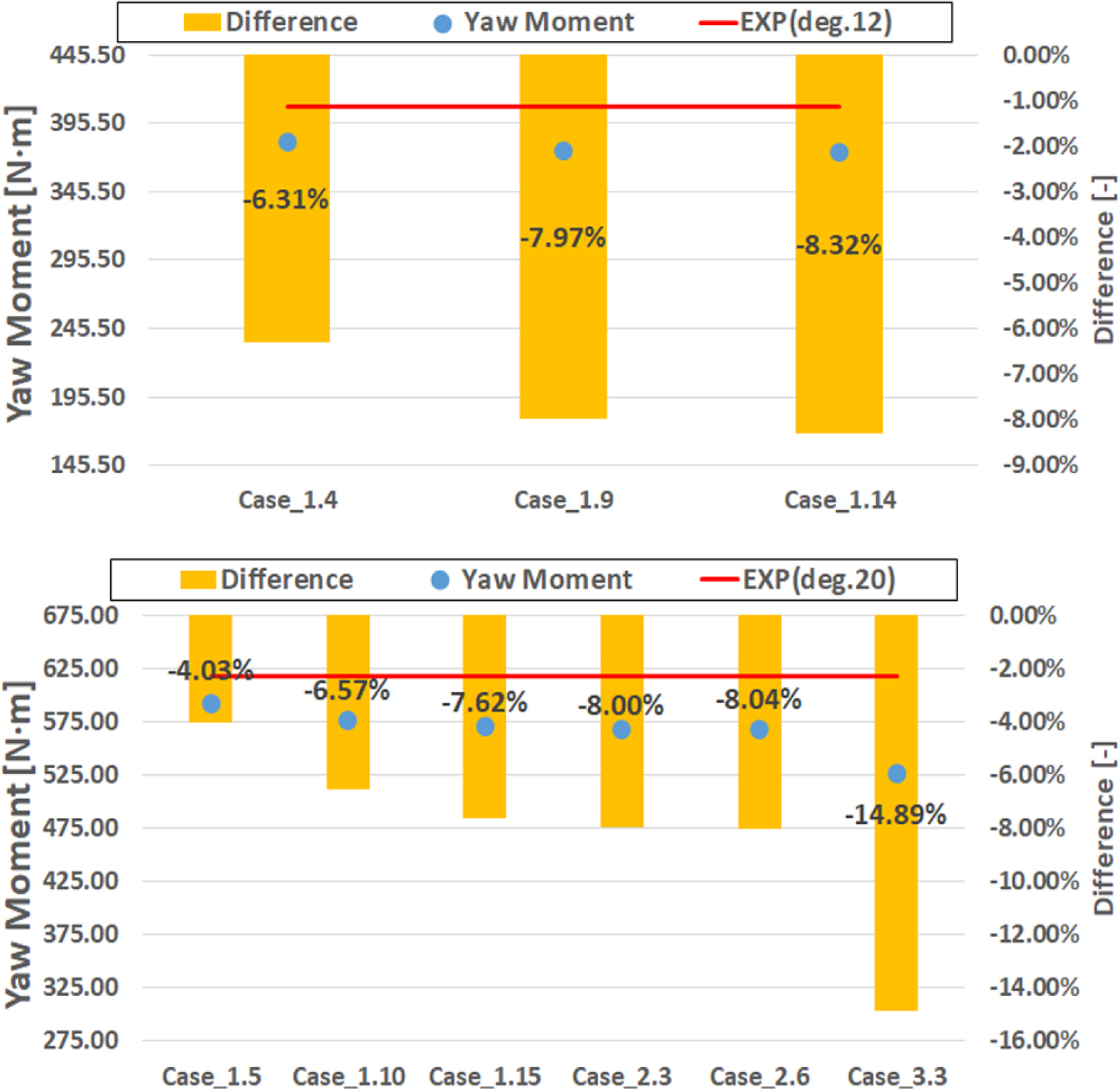
Fig. 9는 수직방향의 무게중심의 변화(100%, 75% 및 50%)에 따른 3자유도, 2자유도 및 완전 구속 상태에서의 사항각별 선체에 작용하는 횡력 및 선수동요 모멘트에 대한 계산결과와 HMRI_EXP(Sung and Park(2015))로 표시된 모형시험과의 비교를 나타낸 그림이다. 사항운동시 선체에 작용하는 횡력의 경우 Fig. 9에 나타낸 바와 같이, 사항각이 비교적 소각도일 때는 계산의 결과에서 차이가 거의 발생하지 않음을 알 수 있으나, 사항각이 커지는 경우부터 그 차이가 비교적 뚜렷하게 나타남을 알 수 있다. 선수동요 모멘트의 경우는 소각도에서 부터 차이가 서시히 나타나서 대각도가 될 때 횡력과 마찬가지로 그 차이가 뚜렷해짐을 알 수 있다. 서론에서 언급한 바와 같이, 수직방향의 무게중심위치의 차이가 횡력 및 모멘트에 차이를 발생 시킬 수 있고 그 차이가 무시하지 못할 수준이라는 것을 나타내고 있다고 판단된다. 각각의 계산 설정 조건별 모형시험 대비 계산과의 차이를 Fig. 10 및 Fig. 11에 나타내었다. 각 그림에서 선으로 표시한 것은 모형시험 결과를 나타내고, 막대 그래프는 모형시험 결과와 계산과의 차이를 표시한다. 또한, 원으로 나타낸 심볼은 계산 결과를 나타내고 있다. 그림에서 왼쪽 축은 물리량을 나타내고 오른쪽 축은 모형시험과 계산결과와의 차이를 비율로써 나타낸 것이다.
각 계산 조건별 횡력에 대한 결과 비교를 나타내고 있는 Fig. 10과 선수동요 모멘트에 대한 결과 비교를 나타내고 있는 Fig. 11을 좀더 구체적으로 살펴보도록 한다. 사항각 12도에 대해서 상하동요, 횡동요 및 종동요에 대한 자유도(이하 3DoF)를 부여한 후 수직방향의 무게중심을 변화시킨 조건(Case 1.4, 1.9 및 1.14)에 대한 결과를 살펴보면, 3DoF이면서 수직방향 무게 중심이 흘수와 일치 하는 조건(Case 1.4)에서 횡력 및 선수동요 모멘트에 대한 계산이 모형시험 결과와 가장 일치하고 있음을 보여 주고 있으며 무게중심이 아래쪽으로 이동할수록 횡력 및 선수동요 모멘트가 모형시험대비 차이가 커짐을 알 수 있다. 이는 일반적으로 탱커의 경우 수직방향 무게중심이 수면아래쪽에 위치한다는 것을 고려했을 때 반대의 경향을 보이는 결과로써, 계산에 사용된 해석자의 정확도가 결과에 영향을 미쳤을 가능성이 있다고 판단된다. 사항각 20도(Case 1.5, 1.10 및 Case 1.15)에서도 동일한 경향을 보이고 있다. 한편, 상하동요 및 종동요에 대한 자유도를 부여한 경우는 횡동요를 고려하지 않았기 때문에 수직방향 무게중심의 변화에 따른 횡력 및 선수동요 모멘트에 변화는 없으나 3DoF에서의 결과와는 차이를 보이고 있으며 모형시험과의 차이가 더욱 증가함을 알 수 있다. 한편, 모든 자유도를 구속한 경우, 횡력의 경우는 3DoF의 결과보다 모형시험에 더욱 가까운 결과를 보이고 있으나 선수동요 모멘트에서 가장 큰 차이를 보이고 있음을 알 수 있다. 따라서, 좀더 정확한 횡력 및 선수동요 모멘트를 추정하기 위해서는 계산 시 수직방향을 무게중심을 정확히 고려한 후 3DoF로 사항 시 선체에 작용하는 유체력 계산을 수행해야 함을 알 수 있다.
4. 결 론
본 연구에서는 수직방향 무게중심의 변화에 따른 횡방향력과 선수동요 모멘트의 차이에 대하여 Open source tool kit인 오픈폼을 이용한 검증을 진행하였다. 검증에 사용된 선형은 조종 성능 연구의 표준 선형인 KVLCC1이 사용되었다.
수직방향 무게중심의 변화를 선저에서부터 흘수까지의 거리를 기준으로 하여 무게중심이 정확히 자유수면상에 존재할 때를 VCG 100%, 흘수의 75%에 존재할 때를 VCG 75% 및 흘수의 50%에 존재할 때를 VCG 50%로 하여 VCG의 변화를 주면서 구속조건을 변경시켜 사항계산을 실시하였으며, 다음과 같은 결과를 도출하였다.
(1) 상하동요, 횡동요 및 종동요에 대해 자유도를 부여한 경우(Case_1.5, Case_1.10 및 Case_1.15)
- 횡력의 경우 수직방향 무게중심의 변화에 따른 계산의 차이는 사항각이 커짐에 따라 증가하며 사항각 20도의 경우, Case_1.5(VCG가 흘수와 같은 위치)의 모형시험대비 오차와 Case_1.15(VCG가 흘수의 절반에 위치)의 모형시험대비 오차간의 차이는 약 4.3%의 차이를 보인다.
- 선수동요 모멘트의 경우 횡력과 마찬가지로 사항각이 커짐에 따라 차이가 증가하는 경향을 보이며, 상기와 마찬가지의 기준으로 살펴보면 사항각 20의 경우 약 3.5%의 차이를 보인다.
- 모형시험 결과와 비교했을 때 차이가 비교적 제일 작은 결과로 횡력과 모멘트를 추정하였다.
(2) 상하동요 및 종동요에 대해 자유도를 부여한 경우(Case_2.3 및 Case_2.6)
- 횡동요가 구속되어있기 때문에 수직방향 무게중심의 변화와 무관하게 힘과 모멘트를 추정함.
- 3DoF의 결과와 비교해서 횡력의 경우, 사항각이 20도의 경우 최대 약 5.2%(Case_2.3의 오차와 Case_2.6의 오차간의 차이)의 차이를 보이고 선수동요 모멘트의 경우 최대 약 4%의 차이를 보인다.
(3) 모든 운동에 대해 구속한 경우(Case_3.3)
- 횡력의 경우 최대 약 2.2%, 선수동요 모멘트의 경우 최대 약 11%의 차이를 보인다.
- 선수동요 모멘트에서 비교적 큰 차이를 보이고 있다.
상기 결과를 바탕으로 판단했을 때, RANS를 활용한 조종유체력 추정에 있어서 자세변화를 고려하는 것이 결과에 영향을 미침을 알 수 있었으며 특히, 모형시험 결과와 비교할 경우 모형시험에서 선정된 조건을 엄밀히 고려할 필요가 있음을 알 수 있다.
한편, 본 연구에서는 탱커 선형에 한정되어 자세변화에 따른 선체에 작용하는 횡력 및 선수동요 모멘트에 대한 연구를 진행하였다. 하지만, 탱커의 경우 컨테이너선 및 LNG 선에 비해 횡동요가 비교적 작은 선형으로써 자세변화의 고려에 따른 횡력 및 선수동요 모멘트의 차이는 다른 선형에 비해 상대적으로 작다고 판단되며, 추후 컨테이너선을 대상선으로 하여 동일한 조건으로 계산을 수행할 필요성이 있다고 판단된다.
Acknowledgements
본 연구는 2016학년도 한국해양대학교 신지교수정착연구비 및 2018년도 한국연구재단의 이공학 개인기초연구지원사업(NRF-2017R1D1A3B03030423)지원으로 수행된 연구결과 중 일부임을 밝히며, 연구비 지원에 감사드립니다.