|
 |
- Search
| J. Ocean Eng. Technol. > Volume 32(6); 2018 > Article |
|
Abstract
This paper introduces a new method of ice load generation in the time domain for the station-keeping performance evaluation of Arctic offshore structures. This method is based on the ice load spectrum and mean ice load. Recently, there has been increasing interest in Arctic offshore technology for the exploration and exploitation of the Arctic region because of the better accessibility to the Arctic ocean provided by the global warming effect. It is essential to consider the ice load during the development of an Arctic offshore structure. In particular, when designing a station-keeping system for an Arctic offshore structure, a consideration of the ice load acting on the vessel in the time domain is essential to ensure its safety and security. Several methods have been developed to consider the ice load in the time domain. However, most of the developed methods are computationally heavy because they consider every ice floe in the sea ice field to calculate the ice load acting on the vessel. In this study, a new approach to generate the ice load in the time domain with computational efficiency was suggested, and its feasibility was examined. The ice load spectrum and mean ice load were acquired from a numerical analysis with GPU-event mechanics (GEM) software, and the ice load with the varying heading of a vessel was reconstructed to show the feasibility of the proposed method.
최근 전 지구적 온난화에 따라 북극해의 빙해 면적이 지속적으로 감소하고 있으며, 2050년대가 되면 1950년대와 비교하여 빙해 면적이 약 50% 까지 줄어들 것으로 예측되고 있다(NOAA, 2017). 이러한 북극 빙해 면적 감소는 북극 지역으로의 해양 접근성 향상을 가져오고 있으며, 최근에는 여름철 북극해를 항해하는 경제적인 북극 항로의 활용이 점점 부각되고 있다. 더욱이 북극 지역의 석유 및 가스 자원 매장량이 전 세계 매장량의 22%에 이를 것이라는 연구 결과가 최근 발표되었다(US Congressional Hearign, 2009). 이러한 북극 개발과 관련한 여건 조성에 따라 북극해를 포함하는 북극지역 개발을 위한 기술 개발이 이루어지고 있으며, 북극해 연안 국가들을 중심으로 극지 자원 탐사 및 생산을 위한 극지해양구조물 기술 개발이 활발히 이루어지고 있다.
극지 빙해 지역의 자원 탐사 및 생산을 위해 설계되는 부유식 극지해양구조물은 그 위치 및 자세를 유지하기 위한 위치유지(Station-keeping) 시스템이 필요하다. Fig. 1은 2004년 북극 지역에서 수행된 Integrated ocean drilling program(IODP)에서 두 대의 쇄빙선(Iebreaker)을 활용한 빙해관리(Ice-management) 작업과 추진시스템을 활용한 동적위치유지시스템(Dynamic positioning system)을 사용하여 빙해에서 위치유지를 하고 있는 드릴쉽(Drillship) 선단을 보이고 있다(Moran et al., 2006). 그림에서 보이는 바와 같이 유빙으로 가득한 극지 해양에서 극지해양구조물이 위치를 유지하기 위해서는 해빙을 필수적으로 고려해야 한다. 특히 선체 주변 해빙에 의한 빙하중(ice load)은 극지해양구조물의 위치유지시스템 설계 및 운영을 위해 필수적으로 고려되어야 한다. 대표적인 극지해양구조물 위치유지방법으로 계류시스템(Mooring system)을 사용하는 방법, 동적위치유지시스템(Dynamic positioning system)을 사용하는 방법, 계류시스템과 동적위치유지시스템을 함께 사용하는 방법 등을 고려할 수 있으며, 이러한 위치유지시스템 설계 단계에서 시간역(Time-domain) 빙하중 고려를 통한 극지해양구조물의 위치유지 성능 평가 및 안전성 평가가 필수적이다.
극지해양구조물의 성능 평가와 관련하여 국내에서는 연구 목적 쇄빙선 아라온(Araon)에 대한 쇄빙성능평가 연구가 경험식, 모형시험, 실선계측의 방법을 활용한 비교 연구로 진행된 바 있다(Lee et al., 2011; Lee et al., 2014). 최근에는 빙하중 추정 경험식을 기반으로 유빙 입사각에 따라 극지해양구조물에 작용하는 빙하중을 추정하는 기법 개발이 수행되었다(Kim and Lee, 2018).
국외에서는 극지해양구조물에 작용하는 빙하중을 시간역에서 고려하기 위해 다양한 수치해석기법들이 제안되었으며, 극지해양구조물에 영향을 주는 많은 수의 유빙(Ice floe)에 대한 운동을 계산하고 유빙-유빙 상호작용, 유빙-극지해양구조물 상호작용을 고려하여 극지해양구조물 선체에 작용하는 빙하중을 추정하는 Discrete element method(DEM) 방법이 가장 활발히 연구되어 왔다. 이러한 DEM 방법은 많은 수의 유빙 운동을 계산하고 유빙 간의 접촉을 포함하는 상호작용을 고려해야 하므로 많은 계산량과 계산 시간을 필요로 한다(Løset, 1994; Kjerstad and Skjetne, 2014; Kjerstad et al., 2015). 이러한 빙하중 추정 수치해석법의 한계를 극복하고자 유빙-유빙 및 유빙-구조물 간의 약한 연성 관계를 고려하고, 병렬구조를 가지면서 뛰어난 부동소수점 연산 성능을 갖는 Graphics processing unit(GPU)를 수치 계산에 직접 활용하는 GPU-event-mechanics(GEM)이 개발된바 있다(Daley et al., 2012; Daley et al., 2014a). Daley 등은 일반적인 그래픽 카드를 갖는 개인 컴퓨터에서 GEM으로 부유식 극지해양구조물에 약 72시간 동안 작용하는 빙하중을 계산하는데 약 36시간이 소요됨을 보였고, 이는 LS-DYNA 기반에서 DEM으로 동일 조건을 계산할 경우 수만 일이 소요됨을 소개하였다(Daley, et al., 2014b).
본 연구는 시간역에서 빙하중을 고려하는 새로운 접근법을 제안하고 그 활용성을 검토하고자 한다. 제안하는 시간역 빙하중 생성 기법은 빙하중이 평균 빙하중(Mean ice load)과 변동 빙하중(Oscillatory ice load)으로 구성됨을 가정하고, 빙해 조건 및 극지해양구조물 운동 상태에 따른 평균 빙하중과 변동 빙하중 요소를 정의하는 빙하중 스펙트럼(Ice load spectrum)을 도입한다. 평균 빙하중과 빙하중 스펙트럼을 기반으로 선박 운동 조건에 따른 빙하중을 합성함으로써 시간역 빙하중을 고려한다.
본 장에서는 모형시험과 수치해석을 통해 획득한 시간역 빙하중 데이터를 분석하여 빙하중이 평균 빙하중과 변동 빙하중요소로 구성되어 있음을 보이고자 한다. 또한 두 빙하중 요소를 활용하여 시간역에서 빙하중을 합성하는 방법을 소개하고, 합성된 빙하중과 모형시험 및 수치해석을 통해 획득한 빙하중을 비교하여 제안한 시간역 빙하중 생성법의 유효성을 검토한다.
본 절에서는 극지해양구조물에 작용하는 빙하중의 특성을 분석한다. 선박해양플랜트연구소(Korea Research Institute of Ships and Ocean Engineering, KRISO) 빙해수조에서 수행된 모형시험을 통해 선박형 극지해양구조물에 작용하는 빙하중을 측정하여 그 결과를 Fig. 2에 도시하였다. 모형시험의 빙해 조건은 빙관리(Ice management) 작업을 통해 큰 해빙들이 적절한 크기의 빙편들로 나누어진 빙해 조건(Managed ice field)이다. 본 모형시험은 200m급 극지용 탱커를 대상으로 수행하였으며, 모형빙은 빙 밀집도(Ice concentration ratio) 10/10의 Pre-swan 조건이며, 빙 두께(Ice thickness) 1.7m, 빙 강도(Ice strength) 1.2MPa이며, 유빙 진행 속도는 0.13m/s이다. 모형시험은 KRISO 빙해수조 Pre-swan 모형시험 절차를 따라 수행되었다(Kim et al., 2018; Jeong et al., 2011). 선수 방향에서 선미 방향으로 유빙이 진행하는 조건에서 극지해양구조물의 전후동요(Surge) 방향으로 작용하는 빙하중의 시계열을 Fig. 2 상단에 도시하였다. 빙하중 시계열의 주파수역 분석 결과인 파워스펙트럼밀도(Power spectral density, PSD)를 그림의 하단에 도시하였고, 빙하중 스펙트럼 형상을 명확히 보기위해 이동평균(Moving average)을 취한 빙하중 파워스펙트럼밀도(Moving average filtered power spectral density, MAF PSD)를 그림에 같이 표시하였다. 빙하중 스펙트럼으로부터 측정된 빙하중은 평균 빙하중과 변동 빙하중으로 구성됨을 확인할 수 있다.
본 연구에서 제시하는 빙하중 생성 기법은 해빙이 존재하지 않는 일반 해역에서의 조류력(Current force)과 1차 파랑 기진력(First order wave exciting force) 생성 방법을 기반으로 개발되었다. 따라서 본 절에서 시간역에서 조류력과 1차 파랑 기진력을 생성하는 일반적인 방법을 소개한다.
일반적으로 해빙이 존재하지 않는 일반 해역에서 해양구조물에 작용하는 조류력은 조류속도와 해양구조물로 입사되는 조류 방향을 나타내는 조류 입사각에 의해 결정되며 조류력 계수(Current force coefficients)를 활용하여 다음과 같은 관계식으로 표현된다.
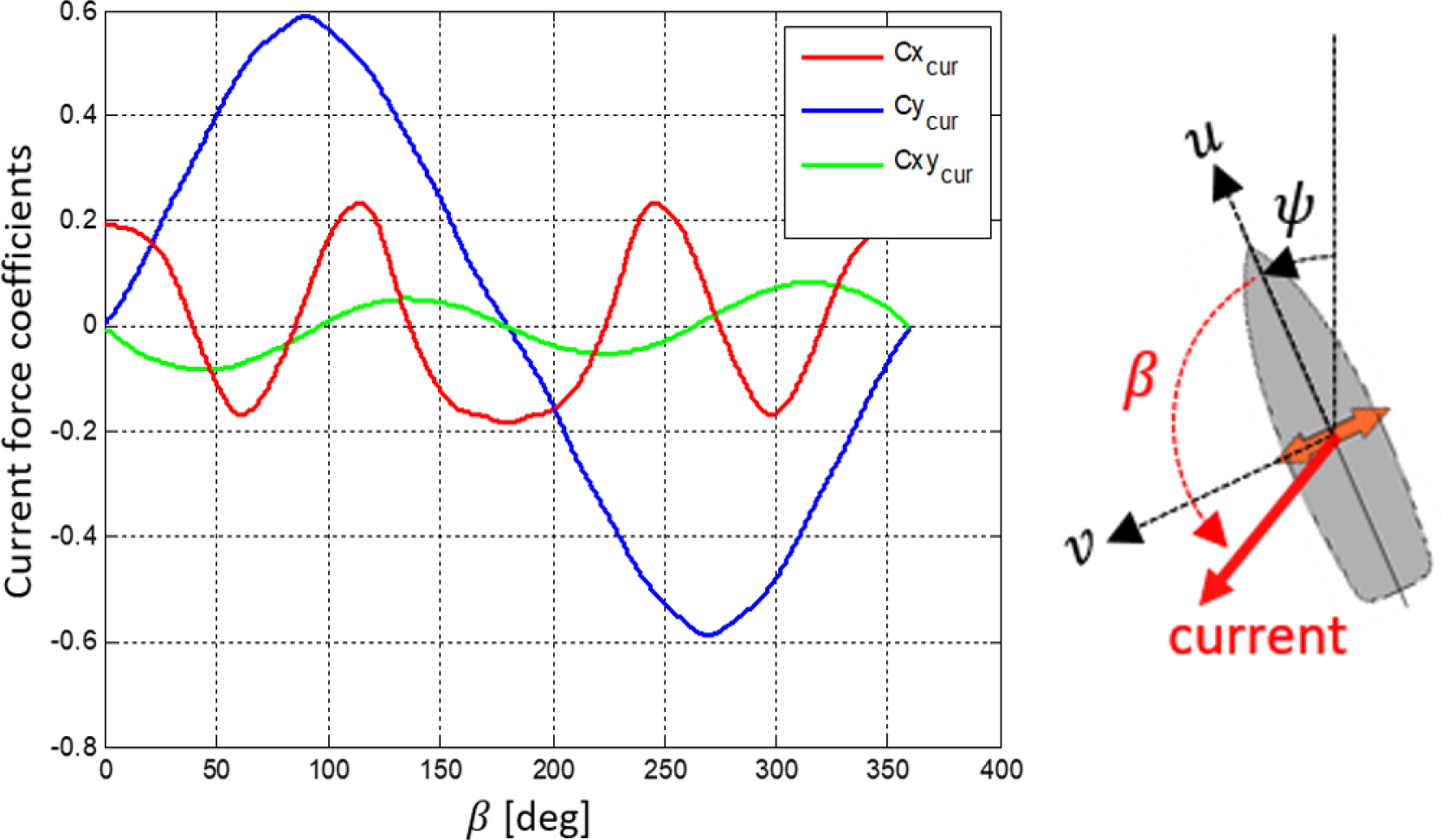
여기서 τcur는 해양구조물에 작용하는 수평면 방향 조류력을 나타내는 조류력 벡터이고, ρw는 물의 밀도이며, Ucur는 조류속도이다. Afc, Asc는 조류의 영향을 받는 흘수 아래 선형의 전후동요(Surge)방향 및 좌우동요(Sway) 방향 투영면적(Projection area)이며, L은 선박의 길이이다. CXcur, CYcur, CXYcur는 각각 전후동요, 좌우동요, 선수동요 방향의 조류력 계수를 나타내며, β는 선박의 몸체고정좌표계(Body-fixed coordinate)에서 정의되는 조류 입사각이다. 아래 Fig. 3은 선박 형상 해양구조물에 대한 조류력 계수와 조류 입사각 β의 정의를 나타낸다. 조류력 계수는 모형시험 또는 CFD (Computational fluid dynamics) 해석을 통해 확보하는 것이 일반적이며, 비슷한 형상 및 비슷한 크기의 선종에 대한 조류력 계수가 존재할 경우 그 크기를 고려한 내삽(Interpolation) 또는 외삽(Extrapolation)을 통해 확보한다(Fossen, 2011).
파랑에 의해 기진되는 1차 파랑 표류력은 파고와 해양구조물에 작용하는 파랑 입사각에 의해 결정되며, 선형전달함수(Linear transfer function, LTF)를 활용하여 다음의 식으로 표현된다.
여기서 τ 1 s t w a v e i L T F R i ( ω j , β ) L T F I i ( ω j , β )
앞서 소개한 조류력 생성 방법과 1차 파랑 기진력 생성 방법을 고려하여 새로운 시간역 빙하중 생성 기법을 다음의 식으로 제안한다.
여기서 i-운동 방향 평균 빙하중 τ ¯ i c e i S i c e i τ ¯ i c e i S i c e i
극지해양구조물의 운용 영역이 결정되어 빙해 조건이 확정되었고 위치유지를 수행하고 있다고 가정하면, 식 (3)은 식 (4)와 같이 단순화 될 수 있다. 실제로 빙해에서 유빙 입사각과 상대속도는 수 시간 동안 급격한 변화를 보이는 경우가 있으나, 다른 빙 파라미터들인 빙 평균 두께, 빙 평균 강도, 빙 밀집도 등은 상대적으로 느린 변화를 보이는 것으로 알려져 있다. 따라서 본 논문에서는 유빙의 진행 방향 또는 극지 해양구조물의 선수각이 변화한다는 조건을 가정하고 식 (4)와 같이 평균 빙하중 τ ¯ i c e i S i c e i
제안한 빙하중 생성기법의 유효성을 검토하기 위해 본 논문의 2.1절에서 소개한 KRISO 빙해수조에서 수행된 200m급 극지용 탱커에 작용하는 빙하중 평가 모형시험 결과를 활용하였다. 모형시험을 통해 계측한 선박형 극지해양구조물의 전후동요 방향 빙하중을 평균 빙하중과 변동 빙하중으로 분석하고 이를 시간역에서 합성한 결과를 Fig. 5에 도시하였다. 또한 계측된 빙하중과 합성된 빙하중 시계열을 통계 분석한 결과를 Table 1에 정리하였다. 합성된 빙하중의 파워스펙트럼밀도는 계측된 빙하중의 파워스펙트럼밀도를 잘 재현하여 주파수 전 영역에서 일치를 보이고 있으며, 빙하중 시계열은 최대값 및 진동 특성이 비슷하게 보이고 있다. 전 주파수 영역에서 일치를 보이는 파워스펙트럼밀도는 합성된 빙하중이 측정된 빙하중의 에너지 량과 주파수 특성을 잘 재현하고 있음을 보이는 것이며, 이는 극지해양구조물의 위치유지 성능평가에서 극지해양구조물에 작용하는 해빙에 의한 외력 에너지 특성을 정성적으로 잘 재현할 수 있음을 의미한다. 또한 Table 1에 정리한 통계분석 결과로부터 평균 빙하중(Mean ice load), 빙하중 실효값(Root mean square of ice load), 빙하중 표준편차(Standard deviation of ice load), 최대 빙하중(Maximum ice load) 등 빙하중이 갖는 대표 통계 특성이 약 5% 이내로 잘 일치하고 있음을 알 수 있다. 본 연구에서는 빙하중을 기술할 때 Fig. 3에 보인 몸체고정좌표계(Body-fixed coordinate system)를 사용하므로, 선수에서 선미 방향으로 작용하는 빙하중은 음의 부호를 갖는다. 극지 해양구조물의 위치유지 성능평가를 위한 시간역 해석에서 주요하게 평가되어야 하는 항목은 극지해양구조물이 정해진 기준 위치로부터 벗어나는 정도와 계류시스템을 사용할 경우 계류삭에 작용하는 최대 장력이다. 이러한 특성을 고려하여 극지해양구조물의 위치유지성능을 평가할 때, 유빙이 이동하는 방향과 같은 방향으로 작용하는 빙하중이 앞서 언급한 위치와 장력에 주요한 영향을 미친다. 따라서 유빙이 선수에서 선미방향으로 흐른다는 가정을 가지고 수행된 본 모형시험 결과에서는 음의 부호로 작용하는 빙하중 최대값이 위치유지성능에 주요한 영향을 미치는 인자이다.
빙히중 추정 수치해석 소프트웨어인 GEM을 사용하여 Han et al.(2017)이 계산한 극지용 Floating production storage and offloading (FPSO)에 작용하는 빙하중 결과를 활용하여 제안한 빙하중 생성기법의 유효성을 다시 검토하였다. Han et al.(2017)의 연구를 통해 계산된 240m급 선박형 극지해양구조물에 작용하는 빙하중 시계열을 평균 빙하중과 빙하중 스펙트럼으로 분석하고 이로부터 빙하중을 합성하여 결과를 Fig. 6에 나타내었다. 방하중 계산에서 환경 조건은 빙 밀집도 8/10, 빙 두께 1m, 빙 강도 2MPa이었으며, 유빙 진행 속도는 0.5m/s로 가정하였고, 이 환경 조건을 Table 3에 정리하였다. 앞서 소개한 모형시험 결과를 활용한 빙하중 합성 결과와 마찬가지로, 수치해석을 통해 추정된 빙하중의 파워스펙트럼 밀도와 제안한 방법으로 합성된 빙하중의 파워스펙트럼 밀도가 좋은 일치를 보이고 있다. 이로서 제안한 빙하중 합성기법이 수치해석을 통해 획득된 빙하중의 주파수 특성을 잘 재현하고 있음을 확인할 수 있다. 또한 수치해석을 통해 계산한 빙하중과 시간역 생성 기법으로 합성된 빙하중의 통계 분석 결과를 Table 2에 정리하였다. 빙하중의 평균값, 실효값, 표준편차, 최대값을 비교하였고 모든 통계 결과의 상호 오차가 약 3% 이내로 좋은 일치를 보이고 있음을 확인하였다.
모형시험을 통해 확보한 빙하중과 수치해석을 통해 계산한 빙하중을 활용하여 본 논문에서 제안하고 있는 빙하중 합성 방법의 유효성을 검토하였다. 모형시험 빙하중과 수치해석 빙하중을 사용하여 제안된 빙하중 합성법을 적용하여 시간역에서 빙하중을 생성하였을 경우, 빙하중의 에너지 량과 주파수 특성이 잘 재현됨을 확인하였다. 더욱이 통계 분석을 통해 합성된 빙하중이 입력으로 사용된 모형시험 및 수치해석 빙하중의 시계열 특성을 약 5% 이내 오차로 잘 재현 하고 있음을 확인하였다. 따라서 제안하는 빙하중 합성 기법을 적용하여 극지해양구조물의 성능평가를 수행할 경우 시간역에서 선수각 변화가 자유롭게 이루어지는 위치유지 작업에서의 위치유지성능과 안전성 검토에서 유효하게 빙하중을 생성할 수 있을 것으로 판단된다.
시간역 빙하중 생성을 위한 준비 및 실행 결과를 본 장에서 다룬다. 앞서 소개한 빙하중 수치해석 소프트웨어인 GEM을 이용하여 Han et al.(2017)이 계산한 빙하중 결과를 사용하여 극지해양구조물의 위치유지 성능평가를 위한 시간역 빙하중 생성 예를 보이고자 한다.
Han et al.(2017)은 GEM 소프트웨어를 활용하여 Table 3에 정리한 빙해환경 조건에서 선박형 극지해양구조물에 작용하는 빙하중을 계산하였다. 몸체고정 좌표계 기준으로 180°부터 130°까지 10°간격 유빙 입사각(β)에 대한 빙하중을 추정하였고 선박형 극지해양구조물의 좌우 대칭성을 고려하여 130°부터 230°까지 10°간격의 유빙 입사각에 대한 평균 빙하중을 분석하여 Fig. 7과 같이 도출하였다. 앞서 언급한 바와 같이 극지해양구조물의 운용 영역이 결정되어 빙해 조건이 확정되고 위치유지를 수행하고 있다고 가정하여 평균 빙하중으로 계산하였으므로 평균 빙하중은 그림에서 보이는 바와 같이 오직 유빙 입사각에 대한 함수로 정리된다. 따라서 극지해양구조물의 위치유지 작업 중 선박의 선수동요만을 고려하여 선체에 작용하는 평균 빙하중을 계산할 수 있으며, GEM 소프트웨어를 통해 계산하지 않은 선수각에 대한 평균 빙하중을 보간법으로 추정할 수 있다.
변동 빙하중을 표현하는 빙하중 스펙트럼을 GEM 추정 빙하중 계산 결과로부터 분석하여 획득하였다. 수치해석을 통해 확보된 빙하중 시계열을 주파수 분석법을 통해 파워스펙트럼밀도로 표시하였고, 유빙 입사각과 변동 빙하중 표현을 위한 주파수 성분에 대한 함수로 가정하여 Fig. 8과 같이 2-파라미터 곡면 그래프(2-parameter surface)로 도시하였다. 평균 빙하중의 경우와 마찬가지로 선박형 극지해양구조물 특성을 고려하여 130°부터 230°까지 10°간격의 유빙 입사각에 대한 그래프 데이터를 구성하였다. 주파수 성분은 파스펙트럼(Wave spectrum)으로부터 파랑 생성시 추천되는 100개 이상의 주파수 개수를 고려하여 결정하였다. 변동 빙하중도 평균 빙하중과 마찬가지로 미리 확보하지 못한 선수동요 운동이 극지해양구조물 운동 중 발생할 경우 보간법을 통해 해당 선수동요 운동에 대한 빙하중 스펙트럼을 추정할 수 있다.
본 논문에서 제시하는 시간역 빙하중 생성 방법을 적용하여 생성된 시간역 빙하중 결과를 Fig. 9에 도시하였다. 새롭게 제안되는 시간역 빙하중 생성법은 극지해양구조물에 작용하는 빙하중을 유빙 입사각에 따라 극지해양구조물에 작용하는 평균 빙하중과 변동 빙하중의 합으로 정의한다. 유빙의 진행 방향이 일정하다고 가정하고 위치유지 작업을 수행하고 있는 극지해양구조물의 선수동요가 발생할 경우, 유빙 입사각은 선박의 선수동요 운동에 의해 결정 된다. 극지해양구조물의 선수동요 운동에 따라 변화하는 유빙 입사각을 가정하여 Fig. 9의 (a)에 도시하였다. 그림에서 보이는 바와 같이 선박의 선수동요 운동은 선수각 ±40°이내에서 장주기 운동과 단주기 운동을 함께 한다고 가정하였고 그 결과 유빙 입사각이 140°에서 220°까지 변화한다고 가정하였다. 가정된 유빙 입사각에 대하여 극지해양구조물에 작용하는 빙하중을 전후동요, 좌우동요, 선수동요 방향에 대하여 각각 Fig. 9의 (b), (c), (d)에 도시하였다. 그림에 도시한 결과로부터 극지해양구조물의 선수동요 운동 또는 유빙 입사각 변화에 따라 극지해양구조물에 작용하는 빙하중 변화가 잘 표현되고 있음을 확인 할 수 있다. 이러한 시간역 빙하중 합성 방법을 통해 극지해양구조물에 작용하는 빙하중을 극지해양구조물의 상태 변화에 따라 적절히 생성할 수 있으며, 계류시스템과 동적위치유지시스템의 성능평가를 위한 시간역 해석에서 빠른 빙하중 생성이 가능함을 확인하였다.
본 논문에서는 극지해양구조물의 위치유지 성능평가 및 운동 성능평가에 활용할 수 있는 시간역 빙하중 생성 기법을 새롭게 제시하였다. 또한 모형시험 결과와 수치해석 결과를 활용하여 새로이 제안된 빙하중 생성 기법의 유효성을 검토하고 그 활용 가능성을 보였다. 제안하는 시간역 빙하중 생성 기법은 극지해양구조물에 작용하는 빙하중이 평균 빙하중(Mean ice load)과 변동 빙하중(Oscillatory ice load)으로 구성됨을 가정하고, 유빙 입사각에 따라 변화하는 평균 빙하중과 변동 빙하중 요소를 정의하는 빙하중 스펙트럼을 도입하였다. 도입된 평균 빙하중과 변동 빙하중을 극지해양구조물 운동 조건, 즉 선수각 변화에 따른 유빙 입사각 변화를 고려하여 시간역에서 합성함으로써 극지해양구조물의 운동 성능평가에 활용할 수 있는 시간역 빙하중을 생성하였다. 제안한 시간역 빙하중 합성 기법의 유효성을 보이기 위해, GEM 소프트웨어를 활용하여 다양한 유빙 입사 조건에 대한 빙하중 시계열 계산결과를 확보하고 시간역 빙하중 합성을 위한 평균 빙하중 데이터와 빙하중 스펙트럼 데이터를 분석하여 제시하였다. 제시된 데이터를 제안된 시간역 빙하중 합성 기법에 따라 생성함으로써 선수각이 변화하는 극지해양구조물에 작용하는 빙하중을 시간역에서 빠르게 생성하였다. 합성된 빙하중은 극지해양구조물의 선수각 변화에 대한 빙하중 변화를 잘 모사하였으며, 극지해양구조물의 초기 설계 단계에서 운동성능 및 위치유지성능 평가를 시간역에서 빠르게 수행할 수 있는 가능성을 보였다.
향후, 제안된 시간역 빙하중 합성 기법을 극지해양구조물 위치유지성능 및 운동성능 평가에 활용할 예정이며, 빙하중 생성에 기여하는 파라미터들의 상관관계를 분석하여 시간역 빙하중 합성을 위한 수식을 고도화 하고자 한다.
후기
본 연구는 선박해양플랜트연구소 주요사업 ‘선박의 빙해역저항성능 고도화 및 위치유지성능 시험평가 기반구축(2/3)’과제(PES9452)와 산업통산자원부 지원의 ‘위치유지와 계류 시스템을 적용하여 ARC7 조건에서 연중운용이 가능한 북극해 기반 부유식 해양구조물 형상 개발’과제(10063405, PNS3170)의 지원으로 수행되었음을 밝히며, 연구비 지원에 감사드립니다.
Fig. 1.
Arctic station-keeping operation of a drillship with ice-management support by icebreakers (Source: IODP): a drilling platform Vidar Viking in the foreground, and icebreakers Oden and Sovetskiy Soyuz in the background managing the drifting sea ice by breaking ice floes to keep the position of the drilling platform stable

Fig. 4.
Linear transfer function (LTF) for 1st wave force in surge direction: (a) real part of the LTF, (b) imaginary part of the LTF
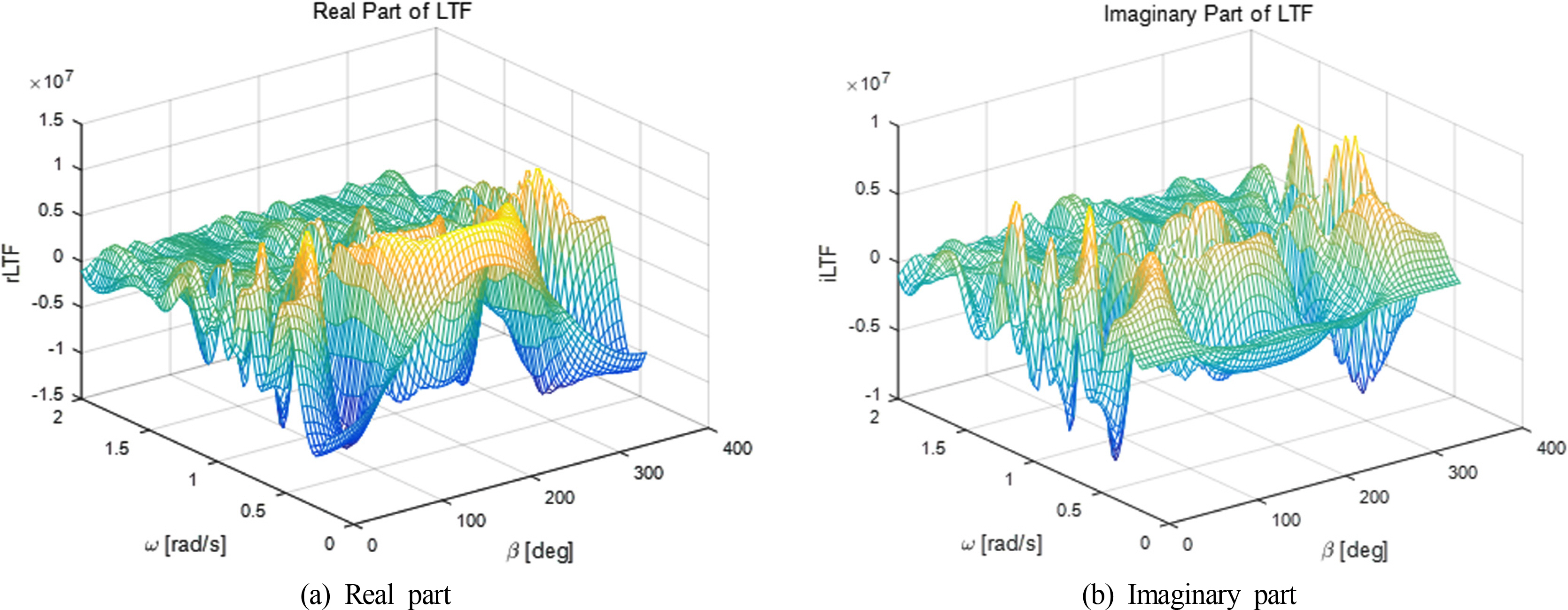
Fig. 5.
Measured ice load in a model test in ice tank of KRISO and reconstructed ice load with the proposed ice load reconstruction method
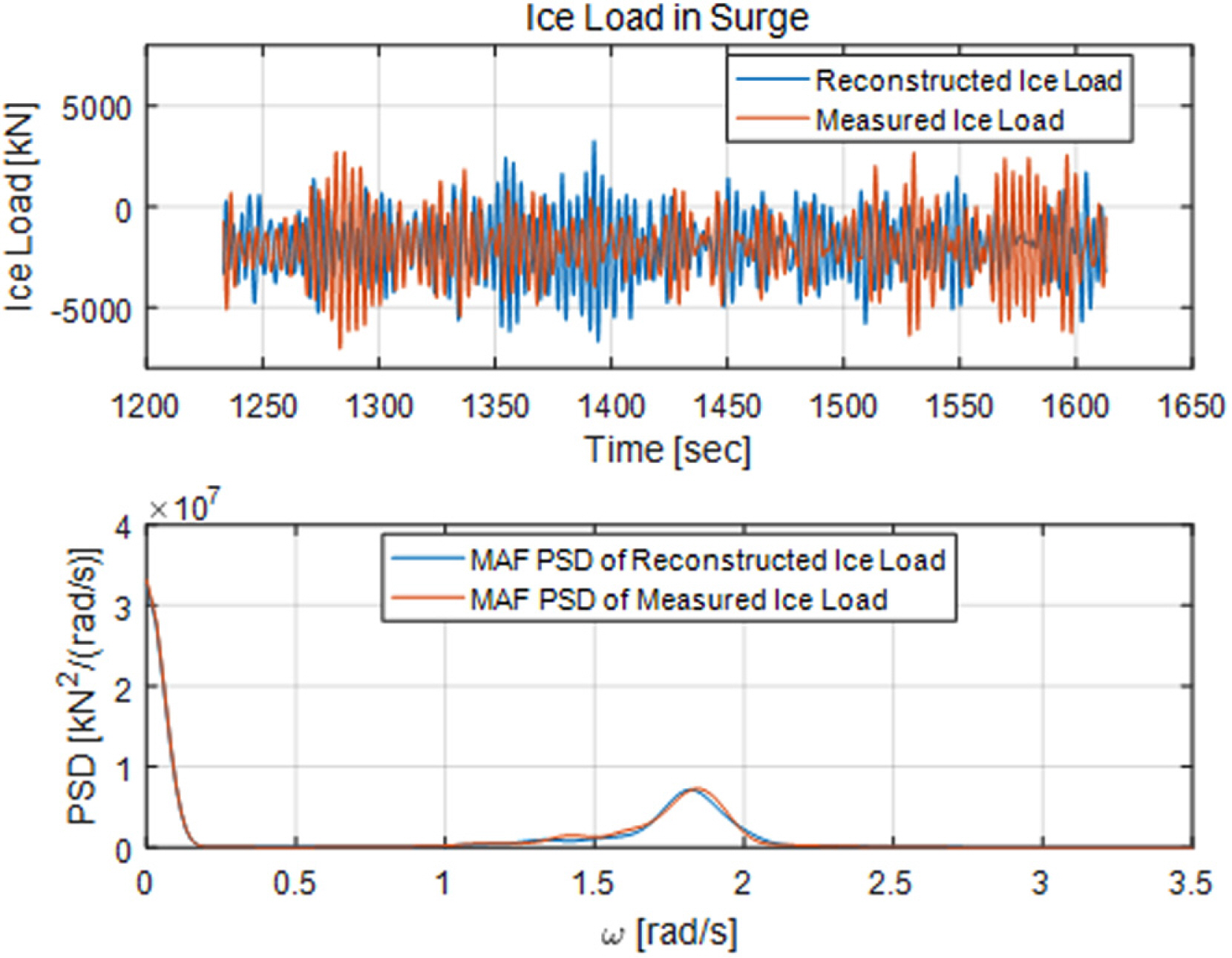
Fig. 6.
Simulated ice load by GEM software and reconstructed ice load with the proposed ice load reconstruction method

Fig. 8.
Ice load spectrum (power spectral density) with the angle of attack by the ice floe drifting
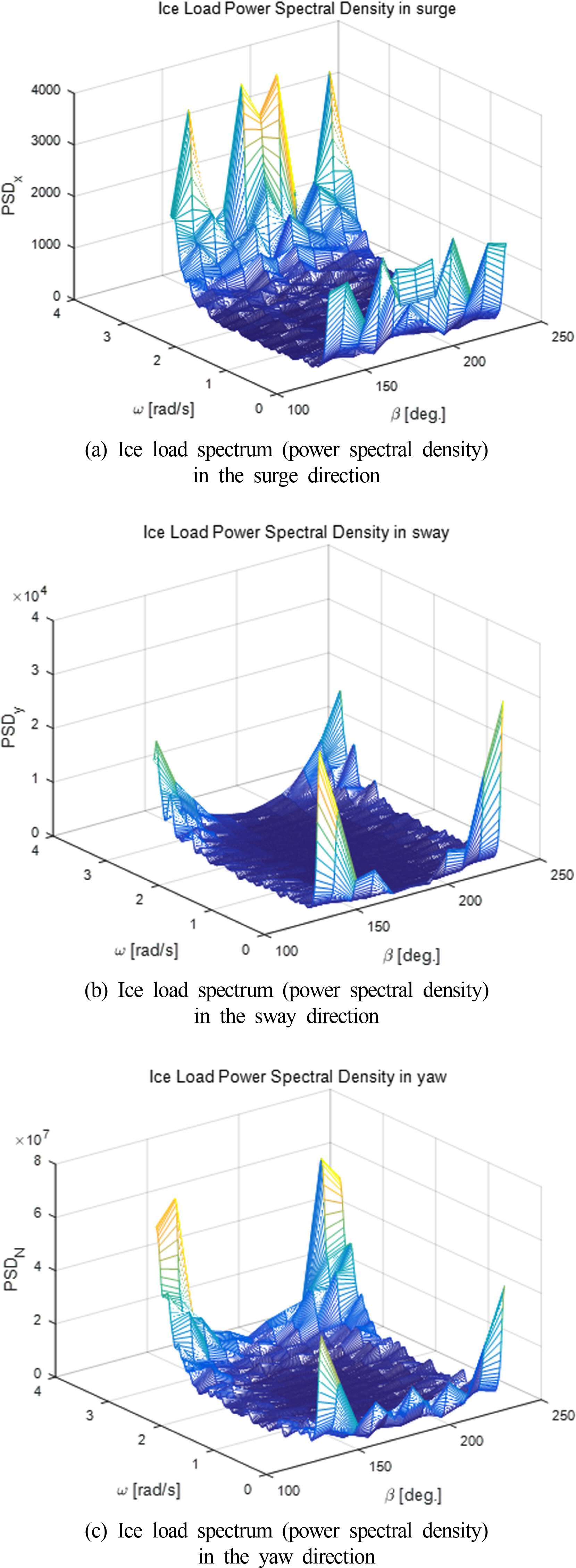
Fig. 9.
Ice load generated in time-domain by the proposed ice load generation method based on the mean ice load and the ice load spectrum
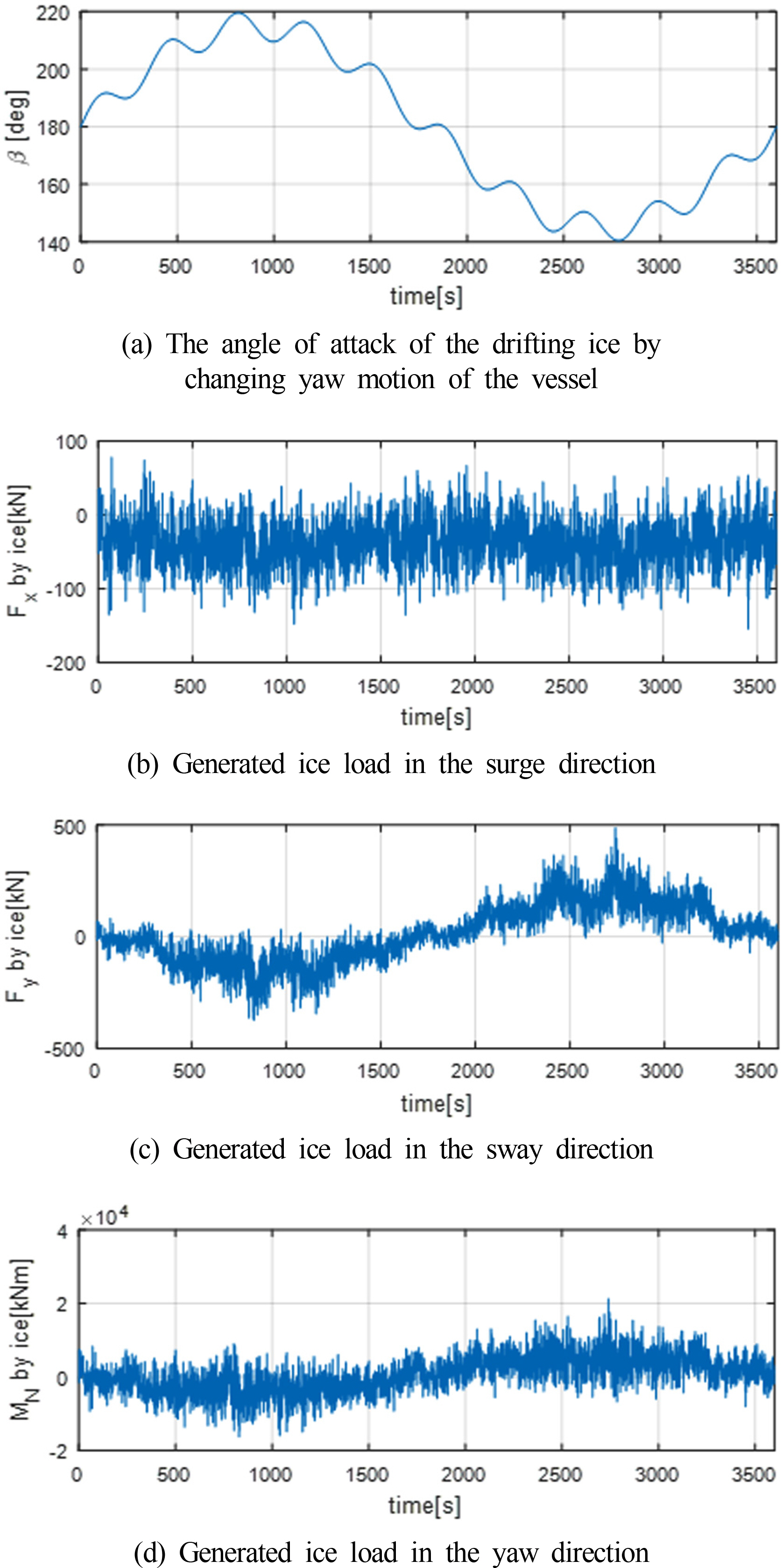
Table 1.
Statistical comparison between measured ice load from a model test and reconstructed ice load by the proposed ice load reconstruction method
Table 2.
Statistical comparison between the simulated ice load by GEM software and reconstructed ice load by the proposed ice load reconstruction method
References
Daley, C., Alawneh, S., Peters, D., Blades, G., & Colbourne, B. (2014b). Simulation of Managed Sea Ice Loads on a Floating Offshore Platform Using GPU-event Mechanics.. International Conference and Exhibition on Performance of Ships and Structures in Ice IceTech; 14.


Daley, C., Alawneh, S., Peters, D., & Colbourne, B. (2014a). GPU-event-mechanics Evaluation of Ice Impact Load Statistics.. OTC Arctic Technology Conference, Offshore Technology Conference..

Daley, C., Alawneh, S., Peters, D., Quinton, B., & Colbourne, B. (2012). GPU Modeling of Ship Operations in Pack Ice. International Conference and Exhibition on Performance of Ships and Structures in Ice Banff; Alberta, Canada.


Fossen, TI. (2011). Handbook of Marine Craft Hydrodynamics and Motion Control. John Wiley & Sons.
Han, S., Kim, HJ., Lee, DY., & Kim, B. (2017). Capability Analysis of Dynamic Positioning for the Arctic FPSO in ICE.. The 24th Port and Ocean Engineering under Arctic Conditions Pusan, Korea.
Jeong, SY., Lee, CJ., Cho, SR., & Chun, EJ. (2011). Component-Based Ice Resistance Prediction Method for Standard Model Ship of MOERI Ice Model Basin. Journal of the Ships and Ocean Engineering, 51(1), 57-64.
Kim, HS., Jeong, SY., Woo, SH., & Han, D. (2018). Study on the Procedure to Obtain an Attainable Speed in Pack Ice. International Journal of Naval Architecture and Ocean Engineering, 10(4), 491-498.

Kim, HS., & Lee, JB. (2018). Estimation Method for Ice load of Managed Ice in an Oblique Condition. Journal of Ocean Engineering and Technology, 32(3), 184-191.

Kjerstad, ØK., Metrikin, I., Løset, S., & Skjetne, R. (2015). Experimental and Phenomenological Investigation of Dynamic Positioning in Managed Ice. Cold Regions Science and Technology, 111, 67-79.

Kjerstad, ØK., & Skjetne, R. (2014). Modeling and Control for Dynamic Positioned Marine Vessels in Drifting Managed Sea Ice. Modeling, Identification and Control, 35(4), 249.

Lee, CJ., Kim, HS., & Choi, KS. (2014). Comparative Study of Ice Breaking Performance According the Scale of Sea Ice on Ice Field. Journal of Ocean Engineering and Technology, 28(1), 28-33.

Lee, SK., Kim, MC., Lee, WJ., Kim, HS., & Lee, CJ. (2011). Study on the Correction Method of Ice Strength and Thickness Applied to the Sea Trial Condition Based on the Ice Model Test Results. Journal of the Society of Naval Architects of Korea, 48(5), 457-464.

Løset, S. (1994). Discrete element Modeling of a Broken Ice Field - Part I: Model Development. Cold Regions Science and Technology, 22(4), 339-347.

Moran, K., Jan, B., & John, WF. (2006). Deepwater Drilling in the Arctic Ocean’s Permanent Sea Ice. Procceeding IODP 302.

National Oceanic and Atmospheric Administration (NOAA). (2017). National Oceanic and Atmospheric Administration Website.. [Online] Available at: <https://celebrating200years.noaa.gov/breakthroughs/climate_model/modeling_seaice.html> [Accessed 01 July, 2018
US Congressional Hearing. (2009). Strategic Importance of the Arctic in Us Policy.. Technical report..
- TOOLS
-
METRICS

-
- 5 Crossref
- Scopus
- 5,052 View
- 100 Download
- Related article in JOET