1. 서 론
조류발전은 조수간만 차로 발생하는 강한 유동 에너지를 터빈의 기계적 회전에너지로 변환하여 전력을 생산하는 해양 재생에너지의 한 종류이다. 정확한 발전량을 예측이 용이하며 댐과 같은 대형 구조물이 필요 없어 기존 생태 환경에 미치는 영향이 매우 적다는 장점이 있다.
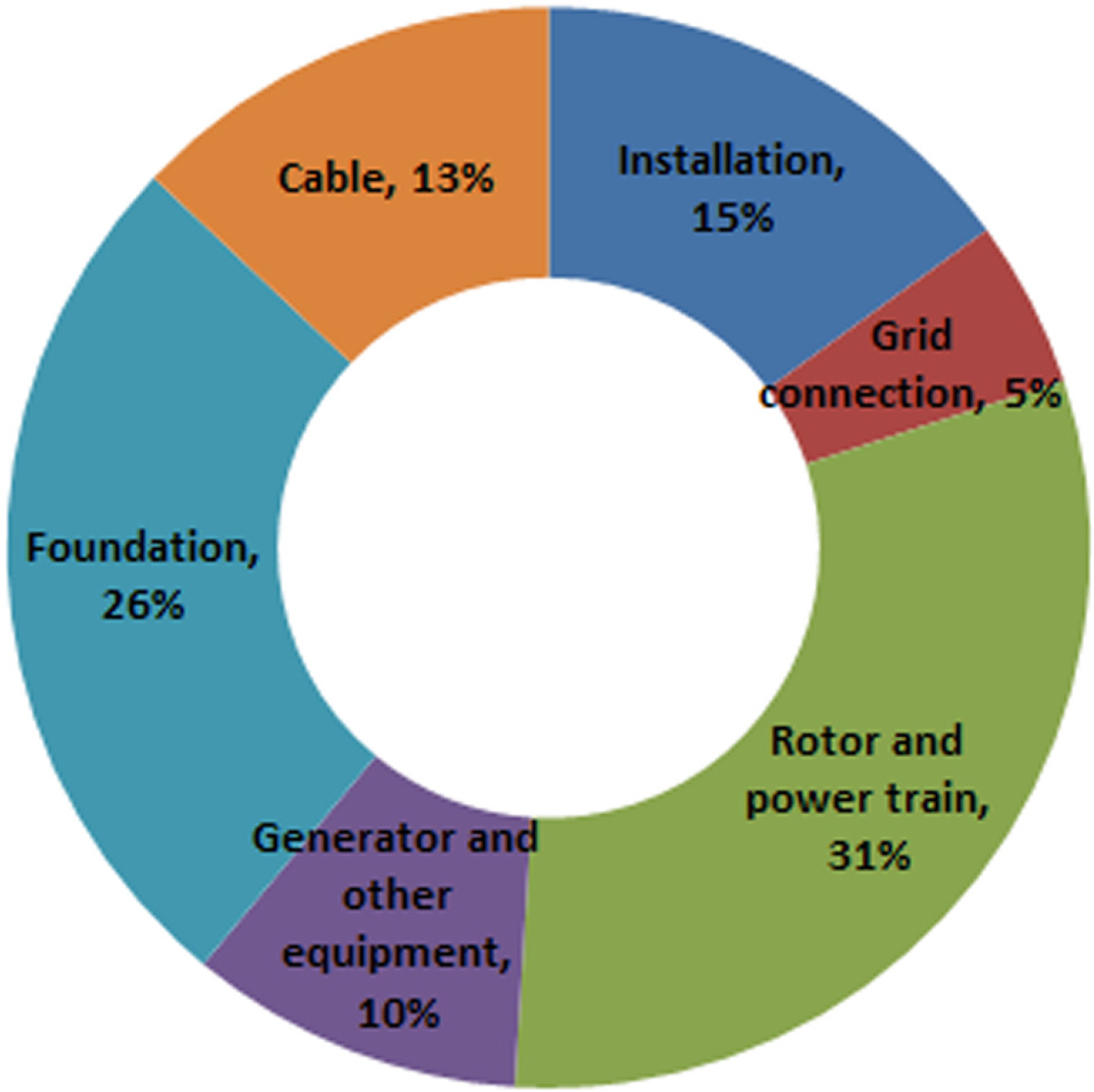
기존의 조류발전장치는 대부분 파일 및 자중 고정식을 사용하였다. 하지만 전통적인 방식의 조류발전 시스템은 지지구조물과 설치비용이 전체의 약 41%를 차지해 실증 연구와 상용화에 큰 걸림돌이 되고 있다(Fig. 1). 또한 지지방식의 특성상 상대적으로 깊은 수심에서 설치 및 유지보수 비용은 매우 높게 증가함으로 현재까지 중대수심에서는 조류에너지의 활용이 제한되었다.
Fu and Johnstone(2017)는 수치해석을 통해 터빈 익형 특성에 따른 다자유도 운동 해석에 관한 연구를 수행하며 다양한 해상 상태에서 계류라인에 작용하는 인장력 및 터빈의 궤적을 분석하였다. Jeffcoate et al.(2016)는 직접 개발한 ProteusDS의 수치해석 프로그램을 이용하여 계류라인에 작용하는 인장력 및 플랫폼의 거동을 분석하였으며 실험을 통해 이를 검증하였다. 뿐만 아니라 계류식 조류발전장치의 실험적 운동성능 고찰에 관한 연구(Jo et al., 2017), 일점계류를 적용한 수평축 조류발전장치에 관한 연구(Jo et al., 2015a) 및 덕트 형상 변화에 따른 부유식 조류발전장치의 운동성능 분석(Jo et al., 2015b) 등 최근 설치 및 유지보수 비용 절감을 위해서 최근 다양한 계류 시스템이 적용된 조류발전장치의 운동특성에 관한 연구가 다수 진행되고 있다.
하지만 이와 같은 연구들은 터빈에 입사하는 유속의 상대속도 변화 등을 고려하지 않아, 계류삭에 작용하는 하중을 정확히 판단할 수 없다. 따라서 본 연구에서는 터빈, 부유체의 연성 효과를 고려하기 위해 부유체-터빈간의 연성 해석을 수행하였다. 조류발전은 현재 일부 선진국을 중심으로 실증연구가 이루어지고 있으며 본 연구를 통해 다루어진 부유식 조류발전장치의 경우 비교할 수 있는 관련연구가 부족하나, 풍력발전의 사례에서 부유식 고정방식을 적용함으로써 설치 및 유지보수 비용을 저감하고 발전 장치의 경제성을 확보한 사례가 있다(Kim et al., 2015). 계류식 지지구조 방식을 적용한다면 구조물의 제작 및 설치는 물론 유지보수 비용을 상당부분 절감할 수 있기에 조류발전 개발에 경제성을 높일 수 있다고 기대되고 있다.
본 연구에서는 터빈과 부유체의 연성해석을 위해 상대속도에 의해 추가적으로 발생하는 터빈의 추력과 모멘트를 도출하였으며, 유의파고, 첨두주기, 유속, 유향 등을 달리하여 총 18개의 Case 설정하여 각각의 환경조건에 대한 부유체의 운동 및 계류라인 안정성을 검토하였다. 또한 터빈의 동작 유무에 따른 부유체의 운동 및 계류라인에 인장력에 미치는 영향에 대해서 분석하였다.
2. 운동해석
2.1 운동 방정식
계류 해석에는 상용 프로그램인 OrcaFlex 10.1a가 사용되었으며, 시간영역 해석을 위한 부유체 운동 방정식은 식 (1)과 같다(Cummins, 1962).
M은 질량, a는 부가질량 계수, B는 감쇠 계수, C는 복원성 계수이며, F는 구조물에 작용하는 각종 외력들을 나타낸다. 각 유체력 계수들은 포텐셜 유동 기반의 방사/산란 문제를 통해 도출할 수 있다. 본 연구에서는 선형 포텐셜 이론 기반의 상용 프로그램인 Wadam으로부터 구조물의 유체력 계수를 도출하였다. 또한 h(t-τ)는 전달함수로서 Convolution 적분을 통해 시간 영역에서의 부유체의 거동 기억 효과를 고려할 수 있다.
2.2 해석 조건
BEMT(Blade element momentum theory)는 블레이드 국부 단면에 작용하는 힘의 관계와 운동량 이론이 서로 결합된 이론으로써, 터빈의 형상 설계 및 하중을 계산할 때 주로 사용된다. Fig. 2와 같은 블레이드 익형 주위의 유동을 보면, 날개요소의 회전 방향 속도(Vw)에 의해 익형으로 입사되는 상대유속(Vr)의 크기와 방향이 결정되며, 상대유속에 의해 수직방향으로 양력, 수평 방향으로 항력이 발생되며 두 힘은 다시 회전방향의 토크와 회전면에 수직인 추력 성분으로 나눌 수 있다.
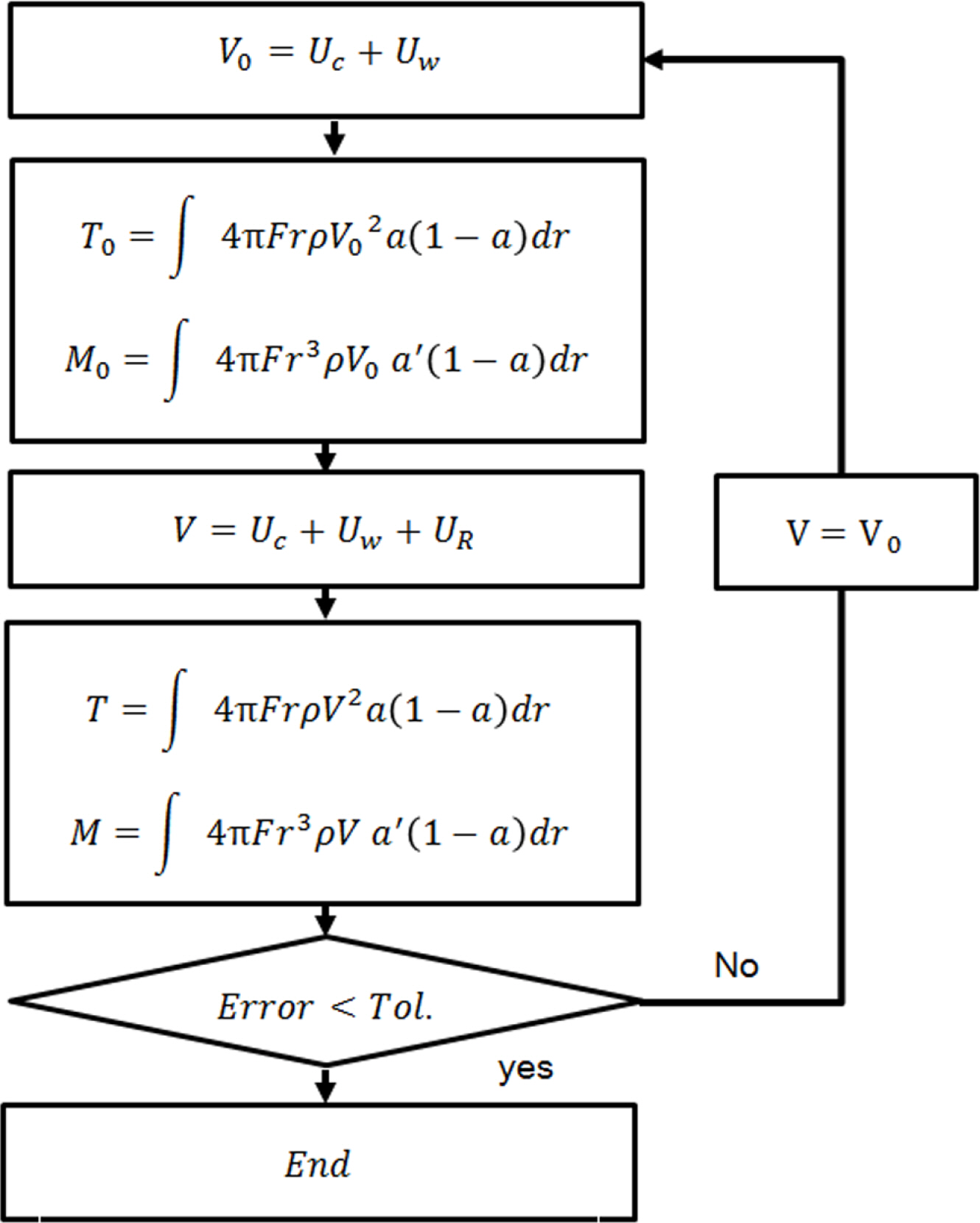
터빈과 부유체 운동의 연성효과를 고려하기 위해 Matlab을 이용한 OrcaFlex 구동 알고리즘을 구성하였다(Fig. 3). V0는 조류와 파도에 의한 터빈으로 입사되는 초기 유속이며, 해양 환경력이 같은 방향으로 입사하는 보수적인 조건을 고려하였으므로 조류속(Uc)와 파입자의 수평속도(Uw)를 단순 합산하였다.
BEMT코드를 통해 파랑 및 조류환경과 더불어 부유체 운동에 영향을 미치는 외력으로 산정되고, 운동 해석에 적용된다. 하지만 부유체의 운동으로 인해 터빈으로 입사하는 유속은 달라지고 발생하는 추력과 모멘트 역시 변화한다. 이를 고려하기 위해 해석이 진행된 후, 부유체 거동으로 인해 발생한 터빈에서의 상대유속(UR)을 도출하고 상응하는 터빈 하중을 계산하여 초기값을 통해 계산된 하중과의 오차를 파악한다. 오차율을 만족하지 못하면 마지막 해석에서 터빈 하중을 발생시킨 유속을 이용하여 재해석이 진행되며 본 연구에서는 속도의 시간 평균을 활용하여 2%의 오차율을 적용하였다.
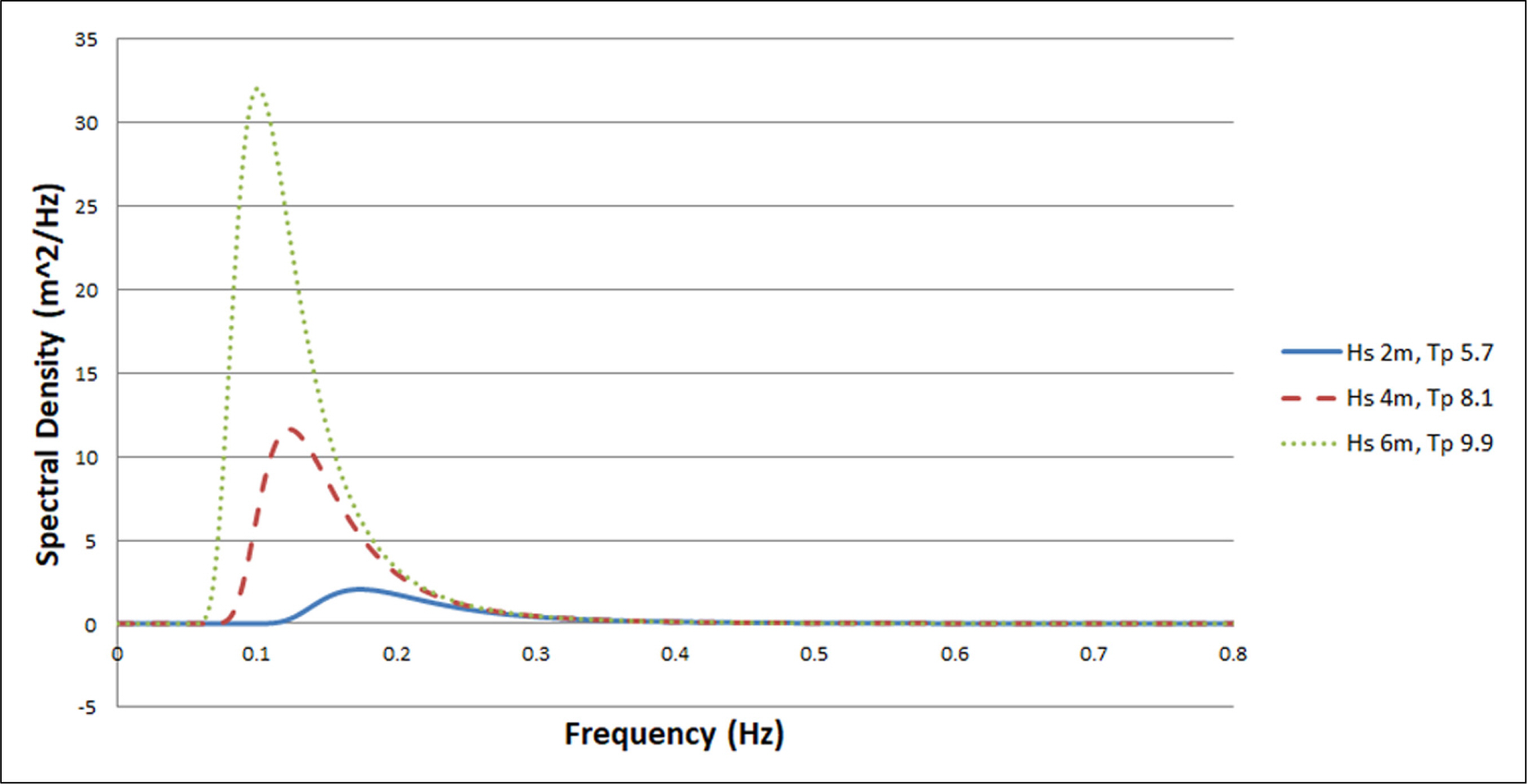
시간 영역 운동해석은 80m 수심을 대상으로 이루어졌으며 유의파고 최대 6m의 ISSC(International ship and offshore structure congress) 스펙트럼 및 Power law 조류 프로파일이 사용되었다(Fig. 4). 경제적으로 조류발전을 적용할 수 있는 최소 유속은 통상 약 1.5m/s로, 국내에선 서남해안에서 제한적으로 발전 가능한 최소 유속이 발생하고 있다. 이는 높은 조수간만의 차와 병목현상을 유발하는 섬지형 등이 요구되기 때문인데, 이러한 환경의 특성을 고려하고 보다 실질적인 연구결과를 도출하기 위해 천해 조건 및 Wave spectrum을 적용하여 다양한 주기의 파도가 복합적으로 작용하는 해석 환경을 부여하였다. 불규칙한 파고와 파주기 및 다양한 유속의 조류가 복합적으로 작용하는 환경에서 터빈과 부유체의 연성 운동 경향을 파악하기 위해 유의파고, 첨두주기, 해양 외력의 작용 방향 등을 구분하여 아래와 같이 18개의 Load case를 산정하였다(Table 1).
1MW급으로 가정한 터빈 2기와 반잠수식 구조물을 이용한 부유식 조류시스템이 구성되었다(Fig. 5). 반잠수식 구조물은 외력에 대해 바지형 형태보다 안정적인 자세 유지성능으로 터빈으로 입사하는 유동의 방향을 유지시킬 수 있으며, Ballasting이 용이하여 수평유지는 물론 계류시스템에 장력을 제어할 수 있는 장점이 있고 이동 및 설치에 용이하다. 본 연구에서는 부유식 조류발전장치의 적용 가능성을 확인하는 차원에서 다양한 해양환경을 가정하였으며 특정 환경에 구조물을 최적화 시키는 것이 아닌, 보편적으로 사용되는 반잠수식 해양구조물을 대상으로 운동성능에 대한 고찰이 이루어졌다. Table 2를 통해 해석에 사용된 반잠수식 구조물의 제원을 나타내었다. OrcaFlex 상에서 제공하는 6D Buoy 모델을 이용하여 터빈을 구현하였으며, Matlab 코드를 이용하여 산정된 추력 및 모멘트를 작용 외력으로 사용하므로 항력과 양력 계수는 고려하지 않았다.
2.3 해석 결과
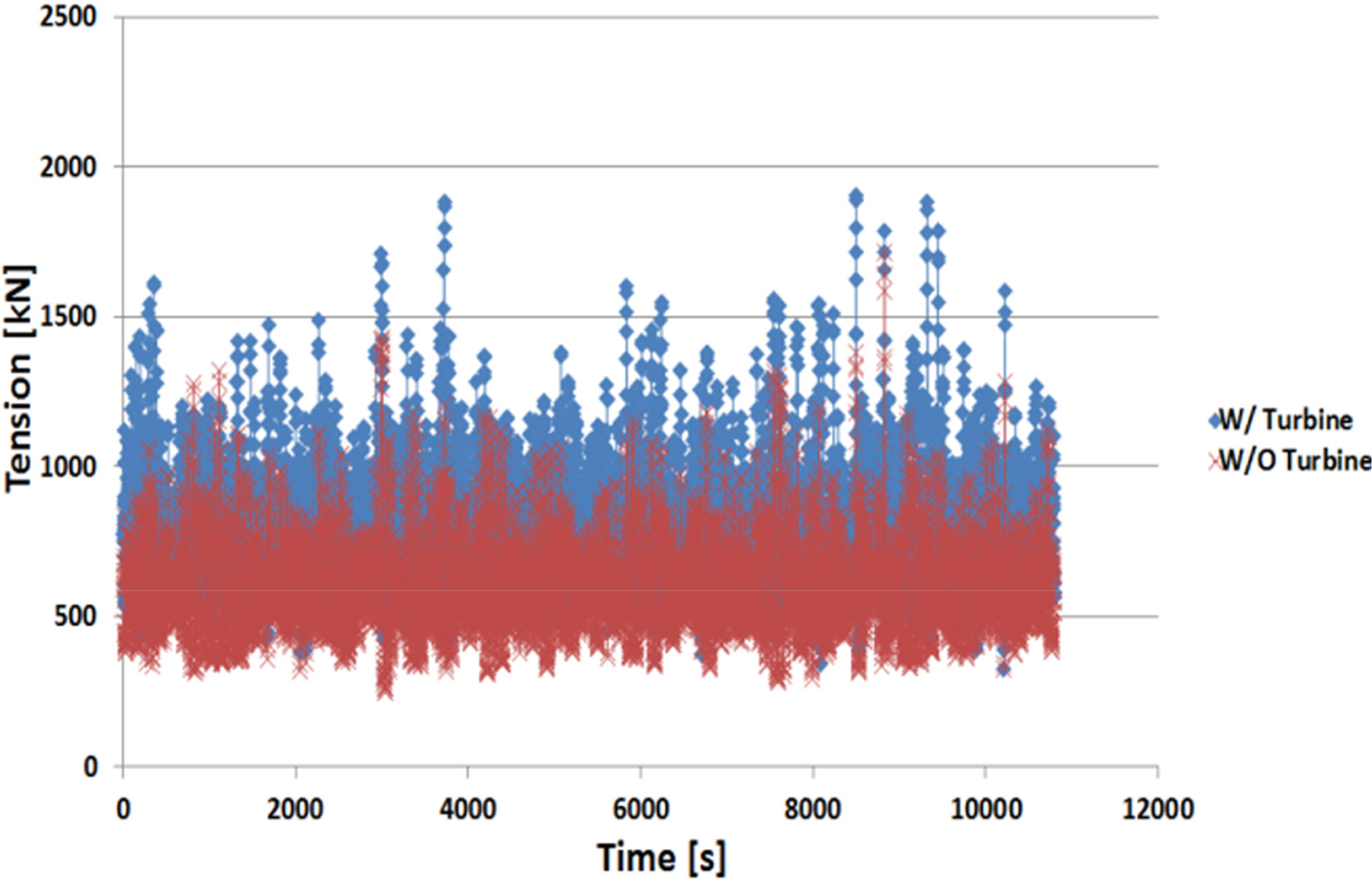
파도와 조류를 포함하는 유속에 부유체 운동으로 발생하는 상대 속도를 고려한 터빈 추력과 모멘트 평균값을 Table 3에 나타냈다. 터빈발생하중은 작용하는 유속의 제곱에 비례하여 증가하는 경향을 확인할 수 있었으며 최대 추력 및 모멘트는 864.4kN 및 564.1kNm로 강한 조류와 파도가 터빈과 수직으로 작용하는 Case 9에서 발생하였다.
3. 계류 안정성 평가
설계된 조류발전장치의 운동해석을 통해 얻어진 계류 체인 발생 하중을 API RP 2SK(Design and analysis of station-keeping for floating structures)를 이용하여 검증하였다(API, 2015). 설계규정에서 제시하는 최소 계류 체인 안전계수는 Table 5와 같이 Intact condition에서 Dynamic 해석 방법을 사용했을 때 1.67로 규정된다.
계류 체인은 Nominal diameter 64mm의 Studless R4 Grade chain으로 구성되었으며 3867kN의 MBL(Minimum breaking load)을 가진다. Table 6에 계류시스템 구성에 사용된 체인의 사양이 나타내었다, 해양 구조물 수명동안의 체인 부식을 고려하여 실제 체인 단면의 직경 90%만을 사용한 MBL의 사용을 제안하고 있으며(DNV, 2012) 본 연구에서도 MBL 감소율 19%를 가정한 Corroded MBL을 설계 기준으로 사용하였다.
계류 체인에서 발생한 최대하중은 1,944kN으로, 가장 큰 유의 파고와 조류속이 적용되어 하중이 In-line condition으로 작용하는Lload case19에서 발생하였다. 이는 Corroded MBL 3,534.8kN 대비 안전계수 1.82를 확보하는 값으로 최소 요구 안전계수 1.67을 상회하는 값이다. Table 7은 사용된 계류 체인의 MBL 및 해석에서 발생한 계류 체인 최대 인장력과 안전 계수를 나타낸다.
4. 결 론
본 연구에서는 조류발전 장치개발 비용 약 41%를 차지하는 유지보수 및 지지구조 비용을 절감할 수 있는 부유식 조류발전장치 운동해석에 관한 연구가 수행되었다. 약 2만 5천톤의 반잠수식 구조물에 1MW급 조류발전 2기를 장착하여 진행된 운동 해석과 계류 설계가 이루어졌으며 부유체 거동에 따른 상대 유속 증가를 고려하기 위해 작성된 Matlab 코드가 활용되었다.
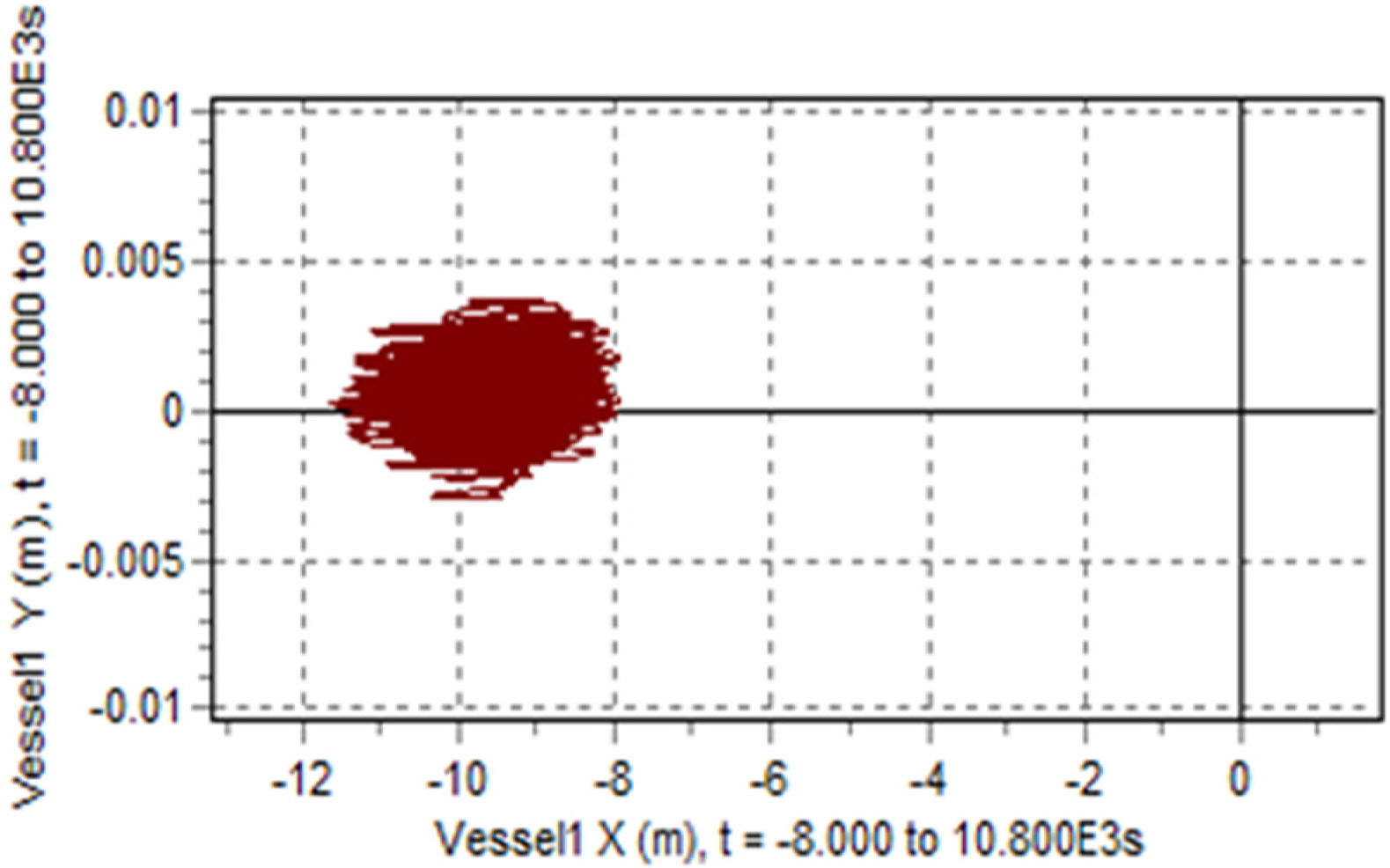
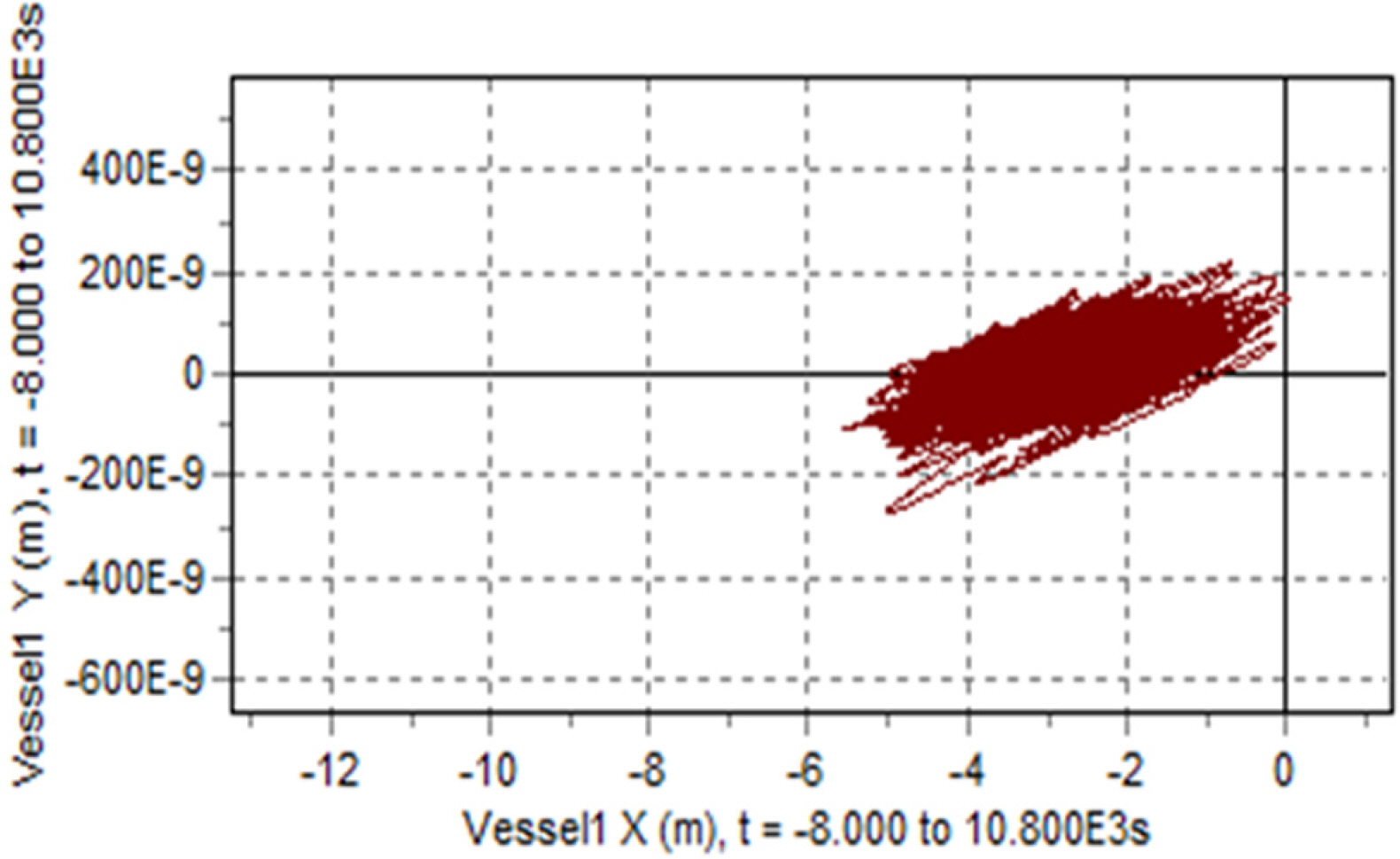
해석 결과, 터빈 하중 최대값은 조류 및 파도가 터빈과 수직으로 입사하는 Case 9에서 발생했지만, 가장 강한 계류 체인 하중은 조류와 파도가 In-line condition으로 작용하는 Case 18에서 발생하였다. 터빈 최대 추력 및 모멘트는 약 864.4kN 및 약 564.1kN.m로 계류 체인 하중 1,903kN에 대해 터빈을 고려하지 않았을 때보다 약 200kN의 인장 하중을 증가시키는 것으로 확인되었다. 또한 터빈은 부유체의 거동 반경을 약 53% 증가시켰으며 최대 거동 반경은 약 11.7m로 확인되었다. 계류시스템은 64mm Studless R4 grade 계류체인 12개를 이용하여 구현하였고, Case 18에서 1.82의 최소 안전 계수를 확보했으며 이는 API (American Petroleum Institute)에서 제시하는 설계 안전 계수 1.67을 상회하는 값이다.
본 연구를 통해 터빈의 동적 효과를 고려한 부유체의 거동 특성을 파악할 수 있었으며 API 기준을 만족하는 계류 시스템이 설계되었다. 연구 결과를 통해 부유식 조류발전장치의 설치 가능성을 확인하였고 추후 이루어질 실증 연구의 기초 자료로 활용될 것으로 기대한다. 특히 부유식 고정 방식을 적용한 조류발전장치에 관한 연구는 개발비용의 상당부분을 차지하는 설치 및 유지보수 비용을 대폭 절감시켜 발전 단가를 경제적인 수준으로 저감시키고 조류발전의 상용화에 큰 도움이 될 것이라 기대한다.