|
 |
- Search
| J. Ocean Eng. Technol. > Volume 32(6); 2018 > Article |
|
Abstract
This paper presents an estimation method for the static configuration of a steel lazy wave riser (SLWR) using the dynamic relaxation method applied to estimate the configuration of structures with strong geometric non-linearity. The lumped mass model is introduced to reflect the flexible structural characteristics of the riser. In the lumped mass model, the tensions, shear forces, buoyancy, self-weights, and seabed reaction forces at nodal points are considered in order to find the static configuration of the SLWR. The dynamic relaxation method using a viscous damping formulation is applied to the static configuration analysis. Fictitious masses are defined at nodal points using the sum of the largest direct stiffness values of nodal points to ensure the numerical stability. Various case studies were performed according to the bending stiffness and size of the buoyancy module using the dynamic relaxation method. OrcaFlex was employed to validate the accuracy of the developed numerical method.
심해 석유 및 가스의 개발이 진행됨에 따라 심해역의 탐사 및 생산 활동이 증가하고 있다(Yang and Li, 2011). 따라서 비용이 저렴한 SCR(Steel catenary riser)은 고온/고압 저항성이 강해 심해 석유 및 가스 생산에 널리 이용되고 있다(Park et al., 2015; Yoo and Joo, 2017). 하지만 초심해(Ultra deep water) 환경에서 SCR은 과도한 자중과 라이저/지반 상호 접촉으로 인한 피로손상의 위험으로 적용에 한계가 존재한다. 이를 극복하기 위해 라이저 중간 부분에 부력재(Buoyancy module)를 설치한 SLWR (Steel lazy wave riser) 개념이 고안되어 개발되고 있다. SLWR은 부력재를 통해 라이저의 인장력을 감소시키고 파도에 기인한 상부 부유구조물의 운동과 라이저를 분리시켜 그 영향을 최소화함으로써, 라이저/지반 접촉으로 인한 피로손상을 감소시키는 장점이 있다(Wang and Duan, 2015). 유연라이저에 비하여 경제적으로 유리한 장점 때문에, SLWR을 심해 석유 및 가스의 생산과 수송에 적용하기 위해 많은 연구가 진행되고 있다.
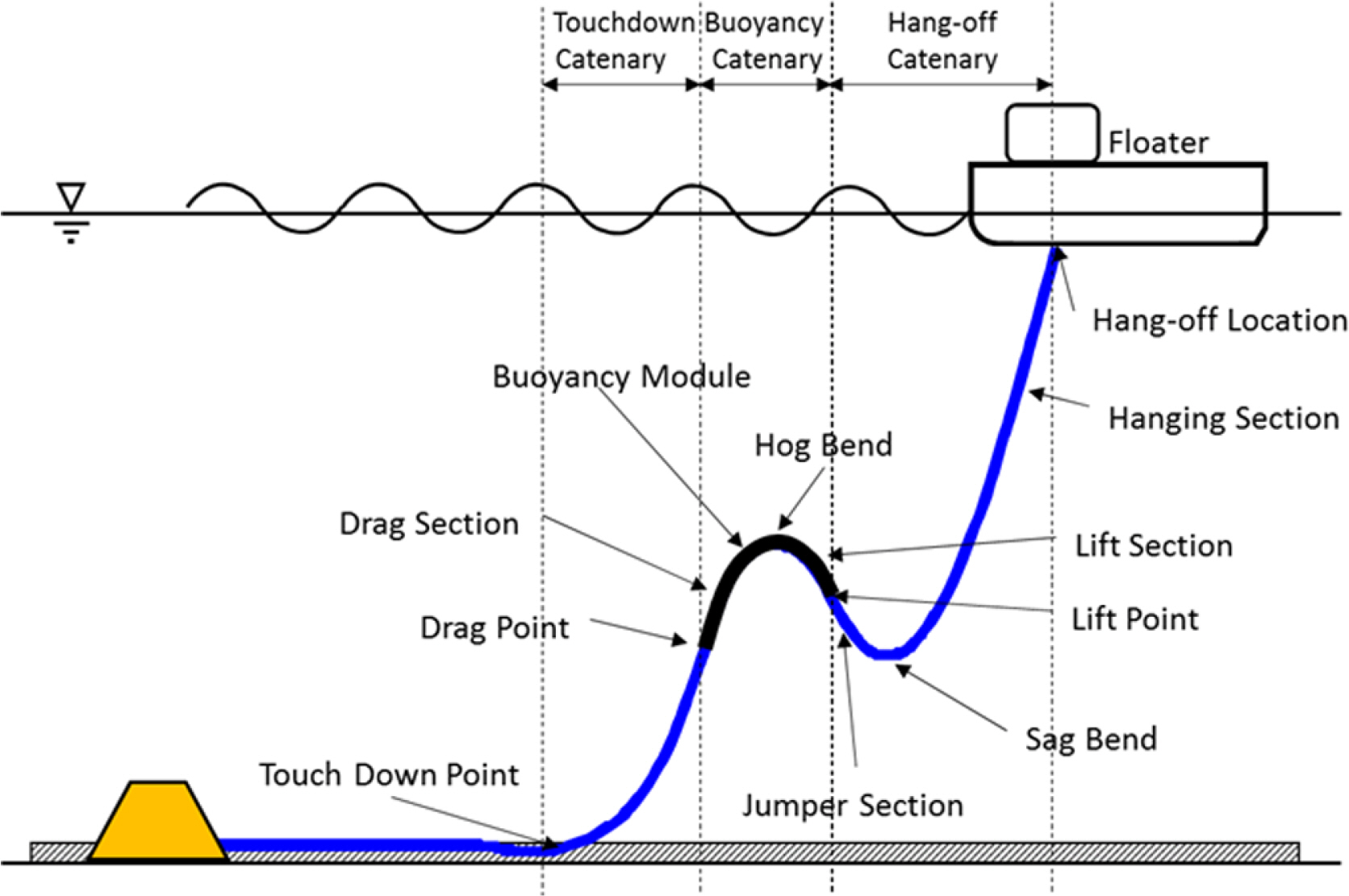
SLWR은 설치되는 부력재에 의하여 Sag/Hog 부분이 형성되어 장력이 비교적 적게 발생한다. 반면, Sag/Hog 영역에서는 기하학적 비선형성이 강하게 나타나기 때문에, SLWR의 정적형상 해석은 라이저 부재의 치수를 결정하는 설계의 중요한 요소이다. Fig. 1에서는 전형적인 SLWR의 전체 형상을 보여주고 있는데, 기하학적으로 비선형성과 굽힘강성을 고려한 정확한 정적형상의 추정이 요구된다.
라이저의 장력이 굽힘강성 성분에 비하여 지배적이지 않은 경우에는, 기하학적 비선형으로 인하여 수치적으로 매우 불안정하다(Jung, 2005). Wang et al.(2013)은 유한차분법을 이용하여 기하학적 대변형의 SLWR의 정적형상을 계산하였다. 그리고 Ruan et al.(2014)은 해석적 방법을 이용하여 탄성지반의 효과를 고려한 SLWR의 비선형 정적해석을 수행하고 OrcaFlex를 이용하여 검증하였다. 이 외에 많은 연구자들에 의해 SLWR의 개념 설계, 정적 및 동적 거동, 그리고 라이저/해저지반 상호작용 등과 같은 광범위한 연구가 수행 되었다(Tahar and Kim, 2003; Ruan et al., 2016; Kim, 2016; Park et al., 2017; Park et al., 2018).
본 논문에서는 동적이완법(Dynamic relaxation method)을 이용하여 저장력(Low tension) 특성을 나타내며 기하학적 비선형성이 강한 SLWR의 정적형상 추정법을 개발하였다. Day(1965)에 의해 제안된 동적이완법은 정적 명시적 비선형 해석법으로 강성행렬을 직접 구하지 않기 때문에 수치해석 알고리즘이 단순하고 계산이 빠르다(Lee and Han, 2008). 따라서 본 연구에서는 동적이완법의 점성 감쇠 정식화를 수치계산에 도입하여 정적해석을 수행하였다. 집중질량모델(Laumped mass model)을 이용하여, 라이저 각 절점에 작용하는 장력, 전단력, 중력, 부력 그리고 라이저/지반 접촉력이 반영된 정적 평형식을 구성하였고 이를 통해 라이저의 유연 구조를 반영였다. 각 절점의 직접강성으로부터 정의된 가상질량을 통해 수치적 안정성을 확보하였다(Barnes, 1994; Hüttner et al.,2015). 수치검증을 위하여 굽힘강성과 부력재의 크기와 같은 SLWR의 주요제원의 변화에 대한 다양한 조건의 수치계산을 수행하였다. 제원 변화에 따른 SLWR의 특성을 확인하고 상용 소프트웨어인 OrcaFlex의 결과와 비교검증하였다.
SLWR 정적 평형 해석을 수행하기 위해 집중질량모델을 도입하였다. 집중질량모델에서는 Fig. 2와 같이 N개의 라인과 N+1의 절점으로 이산화 한다(Hall and Goupee, 2015). 각 절점 Xi는 i의 지점에서 x i , z i T
여기서 ti+1/2는 라이저의 축 강성에 의한 장력, sfi+1/2는 라이저의 굽힘 모멘트에 의한 전단력, wi는 절점에 작용하는 습윤중량(Wet weight)에 의한 자중, 그리고 bi는 지반에 작용하는 수직반력을 의미한다.
장력 ti+1/2는 식 (2)와 같이 정의할 수 있다(Hall and Goupee, 2015).
여기서 EA는 축 강성을 의미한다. 라이저는 유연체로 음의 장력(X i + 1 - X i < l i + 1 / 2
전단력 sfi+1/2는 식 (3)과 같이 정의할 수 있다(Masciola et al., 2014).
여기서 EI는 라인에서 정의된 굽힘강성, mbd, i+1는 절점에서 정의된 굽힘 모멘트 그리고 nx, i+1/2는 라인에서 정의된 법선벡터(Normal vector)이다. 굽힘 모멘트는 식 (4)로 정의되며 각 절점에서 곡률의 계산이 필요하다. 본 연구에서는 효율적인 계산을 위해 Menger 곡률을 사용하였고 식 (5)를 이용하여 계산할 수 있다.
Menger 곡률의 경우, Fig. 4와 같이 3 Point로 계산되기 때문에 스플라인을 이용한 곡률계산에 사용되는 행렬연산이 없어 계산이 효율적이다. 본 연구의 대상인 라이저는 급격한 곡률 변화가 발생하는 경우가 드물기 때문에 Menger 곡률 사용은 타당한 것으로 판단된다.
습윤중량에 의한 체적력은 식 (6)과 같이 부력 그리고 라이저의 내부유체의 중량과 건조중량에 의한 체적력의 상관관계에 의해 정의할 수 있다. 각 체적력은 라인 i+1/2에서 정의되므로 식 (7)-(9)와 같이 평균을 이용하여 절점 i에서 정의하였다.
여기서 ρw는 해수 밀도(1025kg/m3), ρi n는 내부 유체의 밀도, Douter, i+1/2는 외경, Dinner, i+1/2는 외경 그리고 g는 중력가속도(9.807m/s)를 의미하고 e z ^
지반에 작용하는 수직 반력은 식 (10)으로 정의할 수 있다.
여기서 Acon은 접촉면적 zbottom는 해저지면 그리고 kb는 해저의 단위 면적당 강성을 의미한다.
상기 정의된 라이저 절점의 작용하는 내력과 외력들이 정적 평형식이 식 (1)이 모든 절점에서 만족하게 되면 정적 평형을 이루었다고 할 수 있다. 본 연구에서는 기하학적 비선형성을 가지는 SLWR의 정적 평형 상태를 결정하기 위하여 다음 장에 소개할 동적이완법을 사용하였다.
동적이완법은 기하학적으로 비선형성이 큰 케이블 및 박막구조의 형상 찾기(Form finding)에 사용되는 수치기법으로 Day (1965)가 제안한 이후 여러 연구자들(Lewis, 2003; Lee and Han, 2008; Hüttner et al., 2015)에 의해 사용되어 발전되고 있다. 본 방법은 정적 명시적 비선형 해석법으로 강성행렬을 직접 구하지 않기 때문에 수치해석 알고리즘이 단순한 장점이 있다. 즉 정적 비선형 평형식을 수정없이 그대로 적용할 수 있으며 해석결과 역시 강성행렬을 이용한 해석결과와 정확히 일치한다(Lee and Han, 2008).
동적이완법은 식 (11)의 가상 동적평형방정식을 이용하여 정적 평형을 만족시킨다.
여기서 R i t
식 (15)에서 정의된 속도를 이용하여 증분변위를 계산할 수 있으며 이를 통해 절점의 새로운 위치를 식 (16)과 같이 추정할 수 있다. 잔류력 R i t
동적이완법의 경우, 가상질량과 가상감쇠를 적절히 선택함으로써 수치계산의 안정성과 수렴성을 향상시킬 수 있다(Hüttner et al.,2015). 본 연구에서는 수치안정성을 위해 가상질량 Mi를 식 (17)과 같이 설정하였다(Barnes, 1994).
여기서 Si는 절점에 작용하는 최대 강성을 의미하며 식 (18)과 같이 정의하였다.
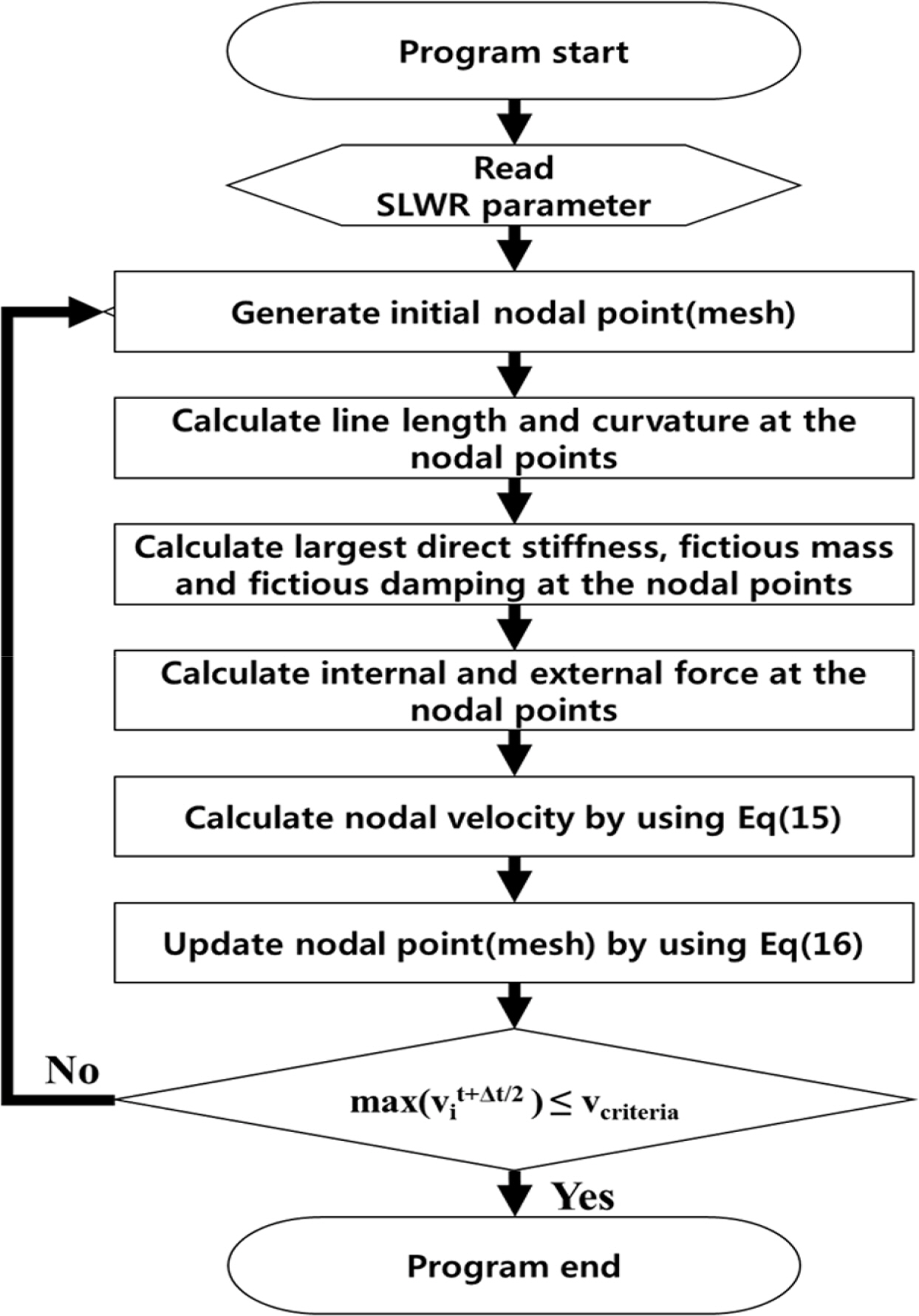
여기서 ζ는 감쇠비를 의미한다. 이상과 같이, 가상감쇠를 이용한 동적완화법을 점성 감쇠 정식화 동적이완법이라 하며 본 연구에 적용하였다. 본 방법의 계산은 Fig. 5와 같이 진행된다.
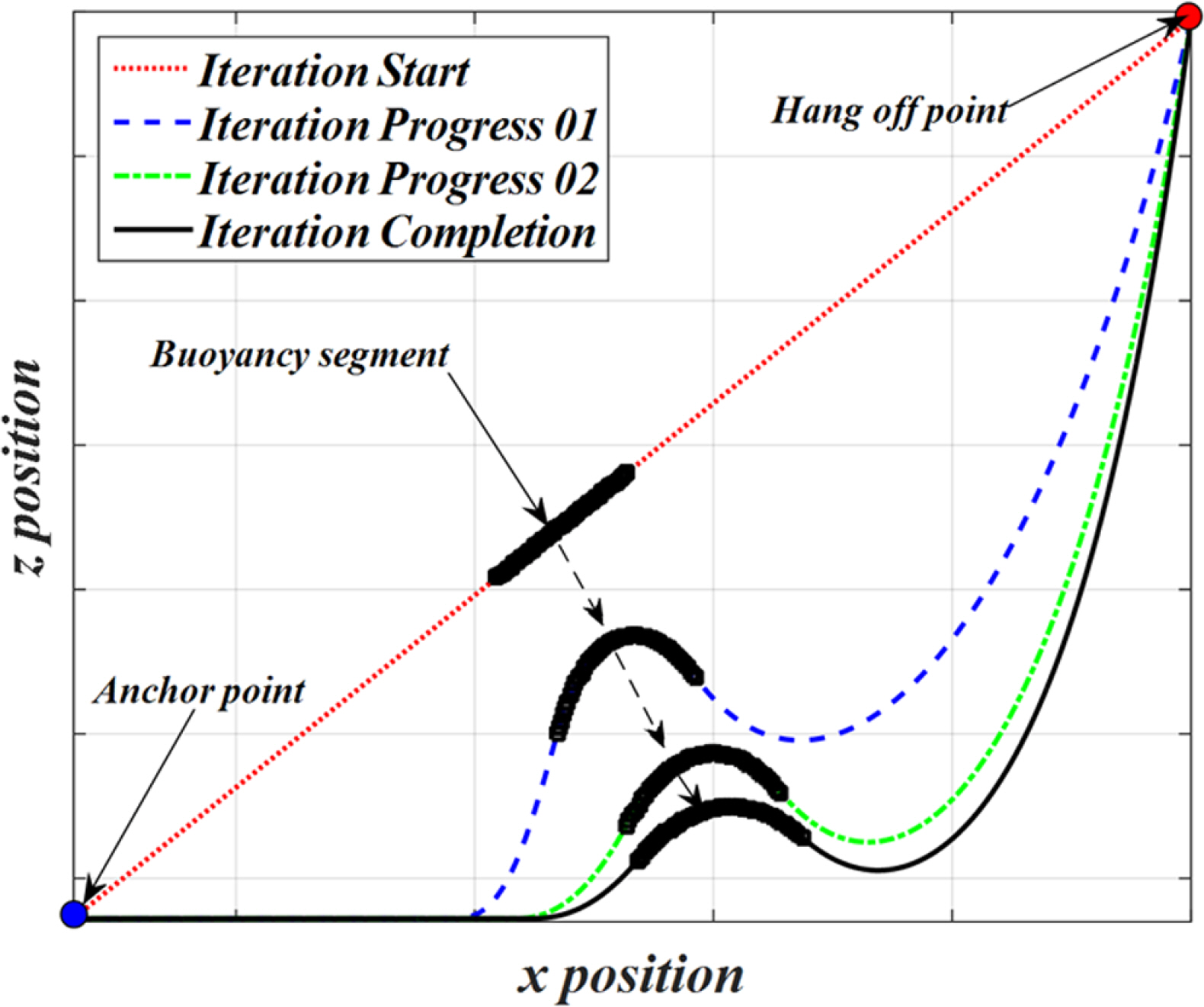
본 장에서는 개발된 수치해석기법을 검증하기 위하여, 다양한 입력조건에서 SLWR의 정적 수치해석 결과를 Orcaflex 값과 비교하여 검증한다. Park et al.(2018)은 SLWR의 주요제원인 부유구조물의 수평운동에 기인한 Hang-off 지점, 부력재의 크기, 내부유체의 밀도 그리고 지반조건의 변화가 SLWR의 초기형상에 미치는 다양한 영향을 보고한 바 있다. 따라서 본 연구에서 제시한 수치계산법이 다양한 조건에서 SLWR의 정적형상을 적절히 모사할 수 있는지 검증하기 위하여, 굽힘강성과 부력재의 크기 변화에 대한 정적 평형 해석을 수행하였다. 부력재 크기의 경우 부력에 직접적인 영향을 주기 때문에 라이저 형상의 대변형을 발생시키는 원인이다. 따라서 부력재의 변화를 통해 다양한 변형에 대한 수치 검증을 하고자 한다. 일반적인 라이저는 길이와 직경의 비가 아주 크기 때문에, 유연한 케이블로 가정할 수 있어 굽힘강성이 미치는 영향이 적다. 본 연구에서는 장력이 굽힘강성 성분에 비하여 지배적으로 크지 않은 비선형성을 모사하고, 극단적인 굽힘강성의 범위까지 검증함으로서 수치방법의 강건성(Robustness) 또한 확인하고자 한다. 검증을 위해 상용소프트웨어인 OrcaFlex의 계산 결과와 비교하였다. 계산에 사용된 SLWR의 제원은 Ruan et al.(2016)에 의해 제시된 Table 1의 제원을 활용하였다.
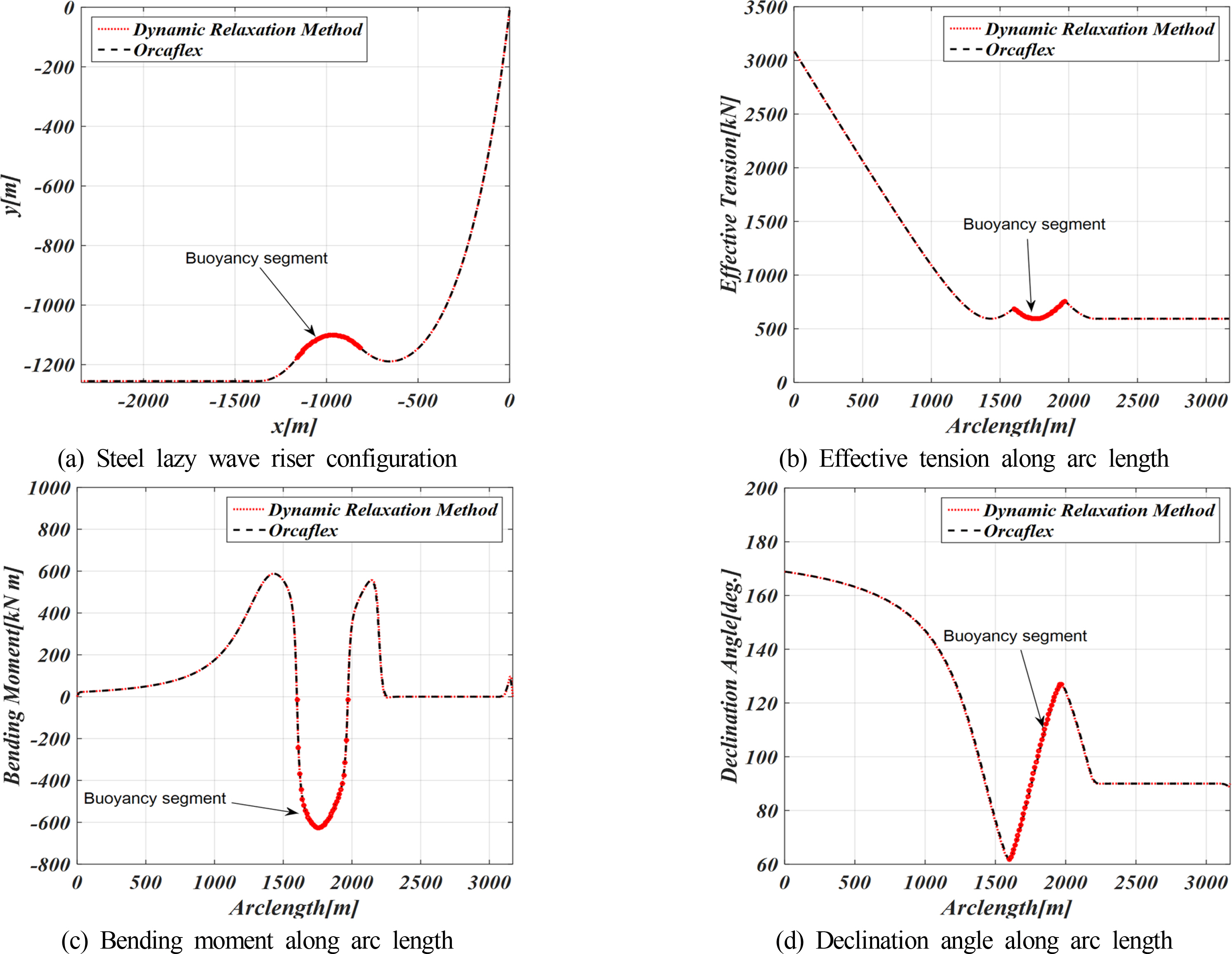
Table 1에 제시된 제원을 이용하여 SLWR의 정적 수치계산을 수행하였다. Hang-off 지점을(0m, -10m), 그리고 앵커 지점을(-2,340m, -1,255m)로 선정하였다. 정적해석의 결과로 형상, 유효장력, 굽힘 모멘트와 경사각을 OrcaFlex와 비교하여 Fig. 7에 도시하였으며, 비교 결과는 Table 2에 요약하였다. 여기서 Ttop는 Hang-off에서 유효장력, Tbot는 해수면 바닥에서 유효장력, Msag는 최대 Sagging 모멘트, Mhog는 최대 Hogging 모멘트, θtop는 Hangoff에서 경사각, XTDP는 해저접촉영역의 x지점 그리고 MTDPMax는 해저접촉영역에서의 최대 굽힘 모멘트를 나타낸다. 대부분의 결과들의 차이가 약 0.5% 이내로 본 연구에서 개발된 동적이완법이 잘 일치함을 확인하였다.
Fig. 7에서는 SLWR의 유효장력, 굽힘모멘트, 경사각 등 중요 변수들의 길이에 따른 변화를 보여준다. 부력재가 설치된 지점에서 Sag/Hog 형상이 나타나며, 유효장력과 굽힘모멘트는 강한 변곡점이 발생하는 것을 볼 수 있다. SCR의 응답값과 비교할 때, SLWR은 강한 비선형 현상이 나타나는 것을 알 수 있으며, 이것은 부력재 설치에 기인하는 것을 알 수 있다.
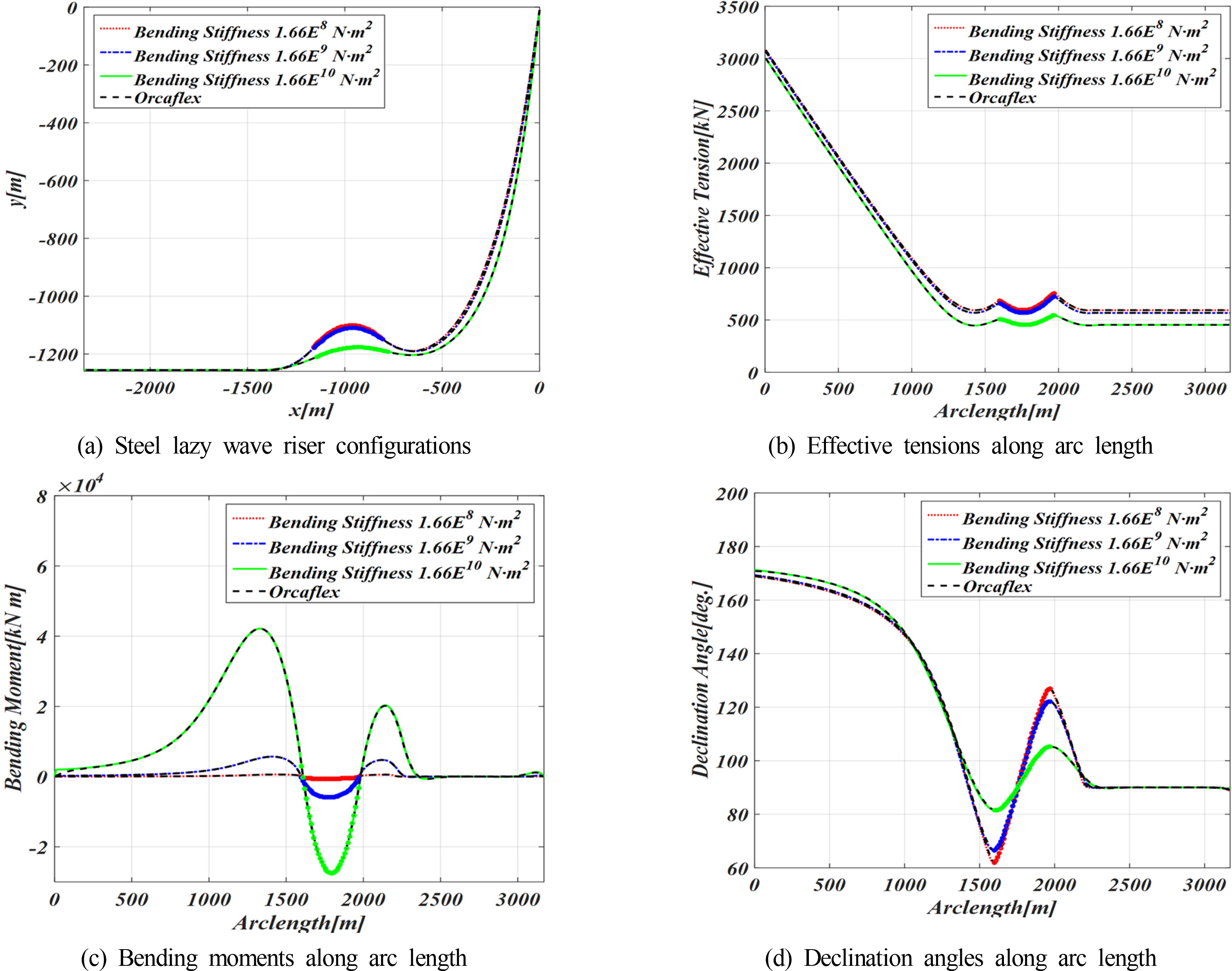
제안된 수치해석 기법의 강건성을 증명하고자, 굽힘강성값 변화에 따른 SLWR의 정적해석값을 분석하였다. 4.1장에서 사용한 굽힘강성(1.66E8N·m2)을 기준으로 1.66E9N·m2 그리고 1.66E10N·m2에 대하여 해석을 수행하였다. 정적해석 결과로 형상, 유효장력, 굽힘모멘트와 경사각을 OrcaFlex와 비교하여 Fig. 8에 도시하였다. 비교 결과는 Table 3에 요약하였다. 대부분의 주요 결과가 OrcaFlex와 1%이내로 잘 일치함을 확인하였다. 굽힘강성이 증가함에 따라 라이저의 곡률변화에 대한 저항이 증가하는 것을 볼 수 있다. 특히, 굽힘강성 증가에 따라 Sag와 Hog 부분의 곡률이 감소하며, 1.66E10N·m2 조건에서는 Sag와 Hog의 변곡점간의 연직거리가 매우 작아서 부력재 부분에서 유효장력값이 크게 변하지 않는 것을 볼 수 있다. 그러나, 굽힘강성의 절대적인 크기로 인하여 굽힘모멘트는 가장 크게 나타난다. 강성의 극단적 증가는 초기 수치적 불안정성이 발생할 수 있지만, 가상 점성 감쇠를 조정함으로 쉽게 해에 수렴시킬 수 있다.
부력재 크기는 SLWR에 직접적으로 작용하는 부력의 영향을 주며 정적형상을 크게 변화시키는 주요 매개변수로, 실제 설계에서 부력재의 길이 및 크기를 통해 SLWR의 설계 형상을 결정한다. SLWR의 기하학적 대변위 해석의 검증을 위해 부력재 크기 변화(직경 변화)에 따른 정적해석을 수행하였다. 형상, 유효장력, 굽힘 모멘트와 경사각을 OrcaFlex와 비교하여 Fig. 9에 도시하였으며, 비교결과를 Table 4에 요약하였다. 대부분의 주요 결과가 OrcaFlex와 0.4%이내로 잘 일치함을 확인하였다. 외경 0.487m의 경우 부력재가 없는 것으로 SCR을 의미하며, 그 형상을 Fig 9에서 확인할 수 있다. 부력재가 큰 외경 1.137m 조건에서는 대변형의 큰 굽힘 형상을 잘 반영하고 있으며, SLWR이 해저면과 맞닿는 터치다운 지점 부근에서도 비선형적인 굽힘모멘트 분포가 나타나는 것을 알 수 있다(Fig. 9(a), Fig. 9(c)).
본 연구에서는 기하학적 비선형이 강한 구조물의 형상추정에 적용되는 동적이완법을 이용하여, SLWR의 정적형상 추정 수치기법을 개발하였다. 라이저의 유연한 구조특성을 반영하는 집중질량모델에서는 라이저의 인장에 의한 장력 및 굽힘 모멘트의 의한 전단력이 내력으로 반영되었고 라이저의 자중, 부력 그리고 라이저/지반 접촉력이 외력으로 반영되었다. 정적 평형 해석을 위해 점성 감쇠 정식화를 이용한 동적이완법이 적용되었다. 수치적 안정성을 확보하기 위해 각 절점의 직접강성으로부터 가상질량을 정의하였다. 개발된 수치해석 기법은 상용 소프트웨어인 OrcaFlex를 이용하여 검증되었다. SLWR의 기하학적 비선형성이 두드러지는 조건인 큰 굽힘강성과 큰 부력재 조건에 대한 해석을 통하여, 개발된 수치기법의 강건성을 검증하였다. 굽힘강성과 부력재의 크기 변화에 따른 수치해석기법의 결과는 Orcaflex 결과와 대부분 1% 이하의 오차율을 나타내어, 개발된 수치기법이 타당하다는 것을 증명하였다.
향후 본 연구에서 개발된 정적형상 추정법을 이용하여 최적형상 추정을 위한 파라메트릭 연구와 라이저 동적해석 프로그램의 수렴성 향상을 위한 초기형상 추정에 활용할 계획이다.
Table 1.
Steel Lazy wave riser parameter (Ruan et al., 2016)
Table 2.
Comparisons for static configuration
Table 3.
Comparison for static configurations according to the variation of bending stiffness
| Item | Unit | Case A (EI = 1.668E8) | Case B (EI = 1.668E9) | Case C (EI = 1.668E10) |
|---|---|---|---|---|
| Ttop | [kN] | 3080.264 (0.04 %)* | 3066.405 (0.064 %) | 3000.97 (0.048 %) |
| Tbot | [kN] | 592.951 (0.227 %) | 567.277 (0.386 %) | 453.469 (0.055 %) |
| Msag | [kN·m] | −625.794 (0.435 %) | −5927.724 (0.606 %) | −27439.516 (0.587 %) |
| Mhog | [kN·m] | 587.879 (0.119 %) | 5686.466 (0.191 %) | 42147.454 (0.019 %) |
| θtop | [deg.] | 168.879 (0.017 %) | 169.301 (0.083 %) | 171.316 (0.290 %) |
| XTDP | [m] | −1359.541 (0.063 %) | −1378.144 (0.113 %) | −1406.521 (0.278 %) |
| MTDPMax | [kN·m] | 556.847 (0.382 %) | 4749.34 (0.506 %) | 20322.152 (1.027 %) |
Table 4.
Comparison for static configurations according to the variation of size of buoyancy module
| Item | Unit | Outer diameter 0.487 m | Outer diameter 1.137 m | Outer diameter 1.256 m |
|---|---|---|---|---|
| Ttop | [kN] | 3224.552 (0.012 %)* | 3080.264 (0.040 %) | 2827.758 (0.055 %) |
| Tbot | [kN] | 598.45 (0.149 %) | 592.951 (0.227 %) | 666.2 (0.178 %) |
| Msag | [kN·m] | - | −625.794 (0.435 %) | −1098.243 (0.382 %) |
| Mhog | [kN·m] | 552.456 (0.404 %) | 587.879 (0.119 %) | 523.924 (0.007 %) |
| θtop | [deg.] | 169.28 (0.01 %) | 168.879 (0.017 %) | 166.335 (0.013 %) |
| XTDP | [m] | −665.341 (0.192 %) | −1359.541 (0.063 %) | −1622.203 (0.002 %) |
| MTDPMax | [kN·m] | - | 556.847 (0.382 %) | 501.217 (0.207 %) |
References
Barnes, MR. (1994). Form and Stress Engineering of Tension Structures. Structural Engineering review, 6(3), 175-202.
Belyaev, AG. (1999). A Note on Invariant Three-point Curvature Approximation.. Singularity Theory and Differential Equations, RIMS, 157-164.
Day, AS. (1965). An Introduction to Dynamic Relaxation. The Engineer, 219, 218-221.
Hall, M., & Goupee, A. (2015). Validation of a Lumped-mass Mooring Line Model with DeeoCwind Semisubmersible Model Test Data. Ocean Engineering, 104, 590-603.

Hüttner, M., Maca, J., & Fajman, P. (2015). The Efficiency of Dynamic Relaxation Methods in Static Analysis of Cable Structures. Advances in Engineering Software, 89, 28-35.

Jung, DH., Park, HI., Wataru, K., & Kim, HJ. (2005). Vibration of Highly Flexible Free Hanging Pipe in Calm Water. Ocean Engineering, 32(14), 1726-1739.

Kim, SJ. (2016). Fatigue Damage of Lazy-wave SCR for Deepwater Offshore Platforms. Journal of the Institute of Industrial Technology(Daejeon University), 27(1), 27-34.
Lee, KS., & Han, SE. (2008). The Development of New Nonlinear Analysis Algorithm by Dynamic Relaxation Method. Journal of the Architectural Institute of Korea Structure & Construction, 24(7), 19-28.
Lewis, WJ. (2003). Tension Structures: from and Behavior.. Thomas Telford: London.
Masciola, M., Jonkman, J., & Robertson, A. (2014). Extending the Capabilities of the Mooring Analysis Program: a Survey of Dynamic Mooring Line Theories for Integration into FAST.. Proceedings of 33rd International Conference on Ocean, Offshore and Arctic Engineering San Francisco, USA: OMAE2014-23508.

Park, BW., Jung, D., Jung, JH., & Kwon, YJ. (2017). Introduction on BOD(Basis of Design) for Concept Design of Steel Lazy Wave Riser. Proceedings of the Annual Autumn Meeting the Korean Society of Ocean Engineers, 370-375.
Park, BW., Jung, D., Jung, JH., & Kwon, YJ. (2018). A Study on the Initial Configuration of SLWR(Steel Lazy Wave Riser) Considering the Effect of Internal Fluid Density and Buoyancy Arrangement.. Proceedings of the Joint Conference of the Korean Association of Ocean Science and Technology Societies (KAOSTS) Jeju, Korea.
Park, KS., Choi, HS., Kim, DK., Yu, SY., & Kang, SC. (2015). Structural Analysis of Deepwater Steel Catenary Riser using OrcaFlex. Journal of Ocean Engineering and Technology, 29(1), 23-34.

Ruan, W., Bai, Y., & Cheng, P. (2014). Static Analysis of Deepwater Lazy-wave Umbilical on Elastic Seabed.. Ocean Engineering, 91, 73-83.

Ruan, W., Liu, S., Li, Y., Bai, Y., & Yuan, S. (2016). Nonlinear Dynamic Analysis of Deepwater Steel Lazy Wave Riser Subjected to Imposed Top-end Excitations.. Proceedings of 35th International Conference on Ocean, Offshore and Arctic Engineering Busan, South Korea: OMAE2016-54111.

Tahar, A., & Kim, MH. (2003). Hull/Mooring/Riser Coupled Dynamic Analysis and Sensitivity Study of a Tanker-based FPSO. Journal of Applied Ocean Research, 25(6), 367-382.

Jung, DH., Park, HI., Koterayama, W., & Kim, HJ. (2005). Vibration of Highly Flexible Free Hanging Pipe in Calm Water. Ocean Engineering, 32(14), 1726-1739.

Wang, J., Duan, M., Fan, J., & Liu, Y. (2013). Static Equilibrium Configuration of Deepwater Steel Lazy-wave Riser. Proceedings of 23th International Offshore and Polar Engineering Conference Anchorage, Alaska, USA: ISOPE; 1: 995-998.

Wang, J., & Duan, M. (2015). A Nonlinear Model for Deepwater Steel Lazy-wave Riser Configuration with Ocean Current and Internal Flow. Ocean Engineering, 94, 155-162.

- TOOLS
-
METRICS

-
- 4 Crossref
- Scopus
- 5,484 View
- 86 Download
- Related articles in JOET