|
 |
- Search
| J. Ocean Eng. Technol. > Volume 32(5); 2018 > Article |
|
Abstract
After an accident involving mooring link failures in an offloading buoy, verification of the fatigue safety in terms of the out-of-plane bending (OPB) and in-plane bending (IPB) moments has become a key engineering item in the design of various floating offshore units. The mooring links for an 8 MW floating offshore wind turbine were selected for this study. To identify the OPB stiffness (OPB moment versus interlink angle), a numerical simulation model, called the 3-link model, is usually composed of three successive chain links closest to the fairlead or chain hawse. This paper introduces two numerical simulation techniques for the 3-link analyses. The conventional and advanced approaches are both based on the prescribed rotation approach (PRA) and direct tension approach (DTA). Comparisons of the nominal stress distributions, OPB stiffnesses, hotspot stress curves, and stress concentration curves are presented. The multiple link analyses used to identify the tension angle versus interlink angle require the OPB stiffness data from the 3-link analyses. A convergence study was conducted to determine the minimum number of links for a multi-link analysis. It was proven that 10 links were sufficient for the multi-link analysis. The tension angle versus interlink angle relations are presented based on multi-link analyses with 10 links. It was found that the subsequent results varied significantly according to the 3-link analysis techniques.
ššÚŠÎ˜š¿Çš šÊš¿Š Girassol šš ÚšÙ ÚŠ¨Ú¥š õ°ŠË šýÇš¡ šš š˜õ° šÇÚš š˜Š˜ š¯õç˜ ÚŠš ÚçÚš˜ OPB(Out-of-planebending) Šˆ´ŠˋÚ¡õ¯ õ°ŠË šýÇš¡š Úš šš¡ššÇ Š¯ÚšÀŠÊ(Jean et al., 2005; Melis et al., 2005; Rampi and Vargas, 2006).
Lim et al.(2010) Š¯ Kim and Kim(2017)š ŠÏÚ˜ õ¯š ŠÏš¯¯ õ°š, õýš˜ ښʚ Ú˜õ¡¯, š¡šËŠ Ëš Ú˜õ¡¯, ŠÏÚ˜š õ°çš¿Ù šÏŠÎ, õñ¡ŠÎ˜õ° ŠÏÚ˜ šš˜õ¯ OPB õ¯šÝš Š₤¡š¿Š šÚËš šÀ¯š˜ÚšŠÊ. 2006Š
ŠÑÚ¯ 2013Š
õ¿šÏ SBM OffshoreŠ šš ãChain out of plane bendingã JIP(Joint industry project)ŠË¥ ÚçÚš˜ ŠÊšÚ OPB õÇŠ ´ š¯õç˜ õý¯õ°¥ŠË¥ š šÚšŠÊ(Rampi et al., 2016a; Rampi et al., 2016b). šÇ JIPŠË¥ ÚçÚš˜ ŠÊšÚ šÊÚš š¯õç˜ Š¯ šš¿ ÚÇš š¯õç˜õ¯ šÚŠšŠÊ. šÇŠÊš šÊš šÊš¥š¥ õ°ŠË šýÇš¡ ŠÏÚ˜š ŠÚ Ú¥ŠÀ šÊÚš šÚÚš˜ ŠˋÇš¡ õç§Ú Ú¥ŠÀŠË¥ Úõ¯ÚšŠÊ. ŠÚ šÊÚ Šˆ´Š¡š ŠÚ š Ú šš ÚÇšš šÚÚšŠÊ. ÚŠšÊ š õ¡š JIP š¯õç˜ õý¯õ°¥ŠË¥ Š¯Úš¥ŠÀ OPB õ¯šÝš šÑš Ú š šŠ õý§Úšš š šÚšŠÊ(BV, 2014).
OPB õ¯šÝš šš¿ ÚÇšš ÚçÚš˜ ŠšÑÚõ¡¯ šÚÇš Úçš 3õ¯ ŠÏÚ˜ŠÀ õ瘚݊ Šˆ´Š¡šÇ šÇšˋŠŠÊ. šÇŠË¥ Š°¡ š¯õ瘚šŠ 3-ŠÏÚ˜ ÚÇšš¥ŠÀ Šˆ
Šˆ
ÚŠÊ. ššš š¡õ¡Š š Ú š¯õ瘊ʚ 3-ŠÏÚ˜ ÚÇš šÊšš OPB Šˆ´ŠˋÚ¡ŠË¥ õ¯š ŠÀ š Š¯šÚÊõ¡¯ šÚš˜ õ¯š Š°š(Prescribed rotation)ŠË¥ š šˋÚšŠÊ. õ¯š Š°šš õ¡¯Š¯Ú 3-ŠÏÚ˜ ÚÇšŠýš š¯š šÀ¯õÝÇš ŠÏšÀÝÚŠŠÀ šý¨ŠýšÏ¡ ŠÏÚ˜ŠË¥ š š Ú õ° š Ú Ú, š¡ŠýšÏ¡ ŠÏÚ˜š š¡šËŠ Ëõ°¥ õ¯š Š°šŠË¥ šš¯´š š¥ŠÀ ŠÑš˜ÚŠ Š¯ˋŠýšÇŠÊ. Š°¡ š¯õ瘚šŠ šÇŠ˜Ú 3-ŠÏÚ˜ ÚÇšŠýš PRA(Prescribed rotation approach)Š¥ Šˆ
Šˆ
ÚŠÊ.
Š¯ŠˋÇ, 3ŠýšÏ¡ ŠÏÚ˜š OPB š¡šËõ¯(Tension angle)š õ¯šÏŠ š¡šËŠ Ë(Tension load)š šÏš ŠÑš˜ÚŠ õ¡¯ŠýšÇ šŠÀšÇ š šŠšŠÊ(Choung and Han, 2016a; Choung and Han, 2016b; Choung and Lee, 2018). Š°¡ š¯õ瘚šŠ šÇŠ˜Ú 3-ŠÏÚ˜ ÚÇšŠýš DTA(Direct tension approach)Š¥ Šˆ
Šˆ
ÚŠÊ. õñ¡ŠÊš DTAõ¯ PRAŠ°ÇŠÊ ښʚ š¡ OPB Šˆ´ŠˋÚ¡š šŠ Ëš š Š¯Ú š šŠ Š¯ˋŠýšÇŠ¥õ° šÈ¥šËÚšŠÊ.
3-ŠÏÚ˜ ÚÇšŠýš Š¯Š¥ õçÙŠÑ šŠ Ë(Hotspot stress)õ°¥ š¡Ú¯ŠÏÚ˜ õ¯(interlink angle)š õÇõ°Š š˜õ¯Ú šÚËš Š¯š š šŠÊ. Š¢ŠÏ šŠŠ¥ 3-ŠÏÚ˜ ÚÇššš š£š OPB õ¯šÝ(OPB Šˆ´ŠˋÚ¡š š¡Ú¯ŠÏÚ˜ õ¯(Interlink angle)š õÇõ°)š OPB š¡šËõ¯õ°¥ š¡Ú¯ŠÏÚ˜ õ¯š õÇõ°ŠË¥ õñŠˆ
Úõ¡¯ šÚ ŠÊšÊ-ŠÏÚ˜ ÚÇšŠý(Multi-link analysis)š š
Š Ë Š¯šÇÚ¯ŠÀ š˜šˋŠŠÊ. Š¯Š¥š 3-ŠÏÚ˜ ÚÇš õý¯õ°¥õ¯ ÚÚ õý¯õ°¥š Š₤¡š¿Š šÚËš ŠÏÊš¯ š˜õ¯ÚŠÊ.
Š°¡ š¯õ瘚šŠ 8MWõ¡ ŠÑš š ÚÇš ÚŠ Ë Š¯š õ¡¯(Li et al., 2018)š õ°çš¿Ù šÏŠÎ 107mm õ°ŠË ŠÏÚ˜õ¯ š˜šˋŠšš õý§š¯ŠË¥ õ¯š Úš˜ ŠýÊš¿ŠÏÚ˜ ÚÇšš šÚÚ õýšÇŠÊ. Šõ¯šÏ 3-ŠÏÚ˜ ÚÇšŠý(PRA Š¯ DTA)š Š¯ŠË¡ ŠÏÚ˜ šÊšŠÑš šŠ Ë šÚŠË¥ Š¿õçÚ õýšÇŠÊ. ŠÚ PRA, DTA, BV õ¯šÇŠŠ¥š¡(BV, 2014)š Š¯ŠË¡ OPB õ¯šÝ, õçÙŠÑ šŠ Ë, õñ¡ŠÎ˜õ° šŠ Ë šÏšÊ õ°šŠË¥ Š¿õçÚ õýšÇŠÊ. ŠÊšÊ-ŠÏÚ˜ ÚÇšš š ÚˋÚ ŠÏÚ˜š õ¯šŠË¥ š¯ƒõ¡¯ šÚ šŠ ÇŠ ÚÇššÇ šÏÚŠ õýšÇŠÊ. 3-ŠÏÚ˜ ÚÇššš š£š OPB õ¯šÝš ŠÊšÊ-ŠÏÚ˜ ÚÇšš š šˋÚš˜ š¡šËõ¯-š¡Ú¯ŠÏÚ˜ õ¯š š šÚ õýšÇŠÊ.
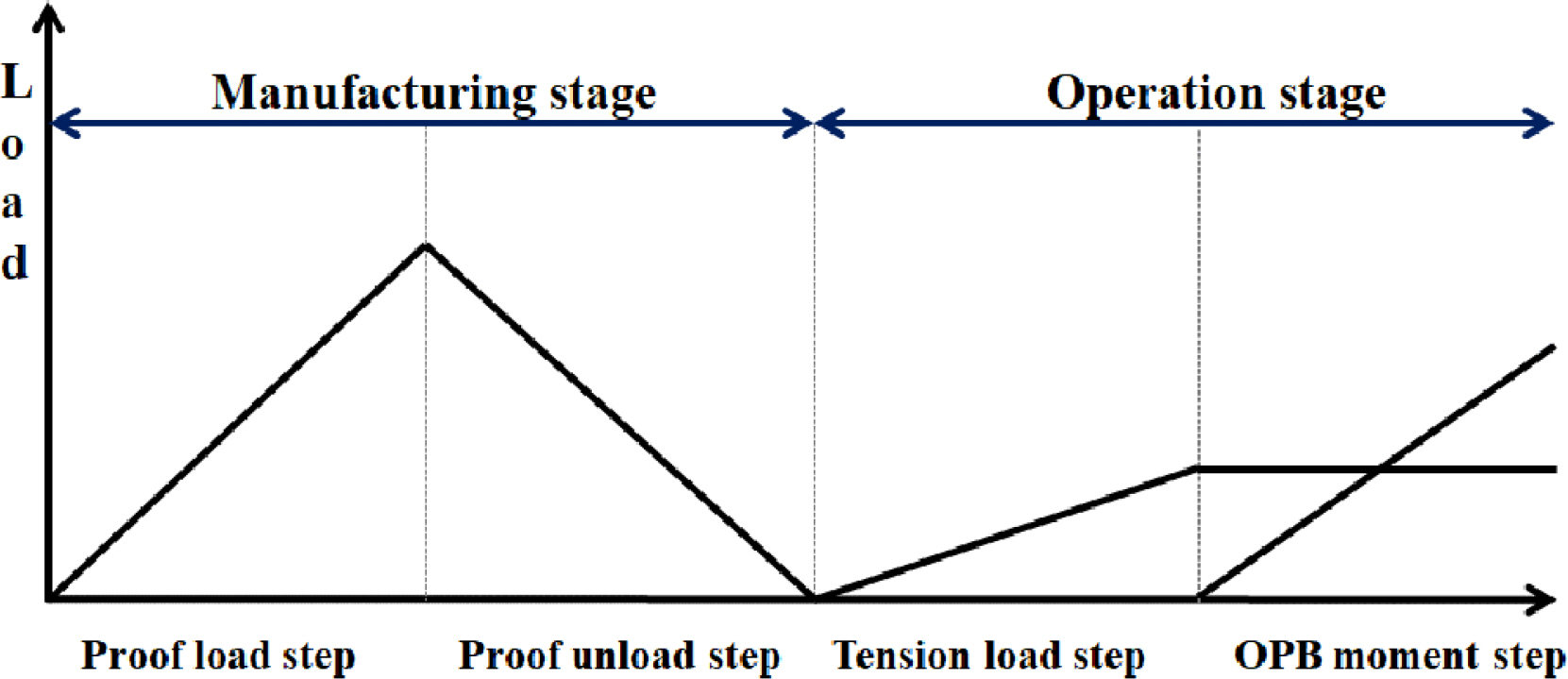
ÚÇš ÚŠ¨Ú¥š š šˋŠŠ Šˆ´Š õ°ŠË ŠÏÚ˜Š šš¯ Š´õ°šš õýš˜ ÚšÊ(Proof load) Ú
šÊÚ¡ŠË¥ õݯš¿ŠÊ. õýš˜ ښʚ šçš ÚŠ´ ÚšÊ(Minimum breaking load, MBL)š 70%ŠË¥ š šˋÚŠÊ(DNV, 2010). šÇš õ¯šÇ Šš õýš˜ ښʚ¥ŠÀ š¡Úš˜ õ°ŠË šýÇš¡ ŠÏÚ˜ š˜šÇš š šÇŠˋÇš ššÝ Š°ÚšÇ Š¯šÚš˜ ŠÏÚ˜Š¥ŠÎ˜ š šÇ ŠˋÇš šÇ ŠšÇšÏŠÊ. ŠšÇšÏ š šÇ ŠˋÇš š šÊš¿ Ú šÇšˋ Š´õ°šš OPB Šˆ´ŠˋÚ¡ŠË¥ š Š¯ÚŠ šš¡šÇ ŠŠÊ. š š¡õ¡Ú õ°¥š š Fig. 1š Š°Çš¡ Š¯š õ¯šÇ 4Š´õ°ŠÀ ŠÑŠËÚ š šŠÊ. šÇŠ õýš˜ ÚšÊ Š´õ°(Proof load step), õýš˜ š Ú Š´õ°(Proof unload step), š¡šËŠ Ë Š´õ°(Tension load step), OPB Šˆ´ŠˋÚ¡ Š´õ°(OPB moment step)šÇŠÊ.
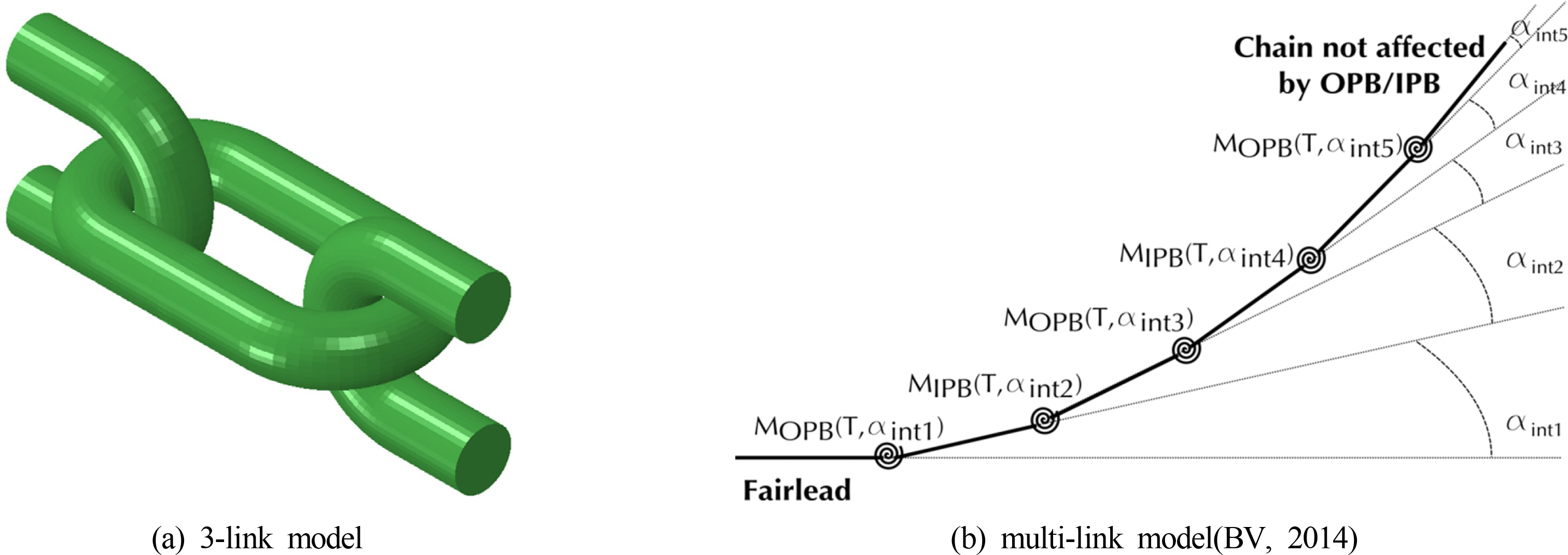
OPB Š¯š õ¡¯õ瘊˥ šÊŠˆ
Úõ¡¯ šÚš˜ 3õ¯š ŠÏÚ˜ŠË¥ Fig. 2š ŠšÚÚšŠÊ. ŠÏÚ˜ #1š š šýÇš õ¯šË õ¯õ¿šÇ ŠÏÚ˜šÇŠˋ¯, ښNJΘŠ(Fairlead) ŠŠ šýÇš¡ Ú¡šÊ(Chain hawse)š šÚš˜ šš Ú õ瘚ŠšŠÊõ° õ¯š ŠŠÊ. ŠÏÚ˜ #2Š OPB Šˆ´ŠˋÚ¡ŠË¥ õý§ÚÚŠ ŠÏÚ˜šÇŠÊ. ŠÏÚ˜ #2š OPB Šˆ´ŠˋÚ¡Š ŠÏÚ˜ #1õ°¥ ŠÏÚ˜ #3õ°¥š ŠÏš¯¯Š Ëš šÚš˜ Š¯šÚŠÊ. šÎ ŠÏÚ˜ #2Š ŠÏÚ˜ #1š ŠÏš¯¯Š Ëš šÚš˜ šÏšÏŠõ° , ŠÏÚ˜ #3š šÚš˜ ÚÀÚšÊšÇ õ¯Úǚϊ š¡ÚŠ°ÇŠÀ õ¯šÈ¥Š š šŠÊ. š¡šËŠ Ë Tš š¡ÚŠ°Çš šÏõçÚŠ šÝŠÑšÇ OPB Šˆ´ŠˋÚ¡ŠË¥ š Š¯ÚŠ₤ŠÀ, š (1)õ°¥ õ¯šÇ OPB Šˆ´ŠˋÚ¡ŠË¥ š šÚ š šŠÊ. š˜õ¡¯š öÝToŠ š¡šËŠ Ë Tš š¡šËõ¯š, öÝinto1Š ŠÏÚ˜ #1õ°¥ ŠÏÚ˜ #2š˜šÇš š¡Ú¯ŠÏÚ˜ õ¯(šý¨ ŠýšÏ¡ š¡Ú¯ŠÏÚ˜ õ¯), Lš š¡ÚŠ°Ç(ŠÏÚ˜)š õ¡¡šÇšÇŠÊ. DTAŠ šÇŠ˜Ú OPB Šˆ´ŠˋÚ¡ Š¯š õ¡¯õ瘊˥ š Š¯ÚŠŠÀ õ¯Š¯Š Š¯ˋŠýšÇŠÊ.
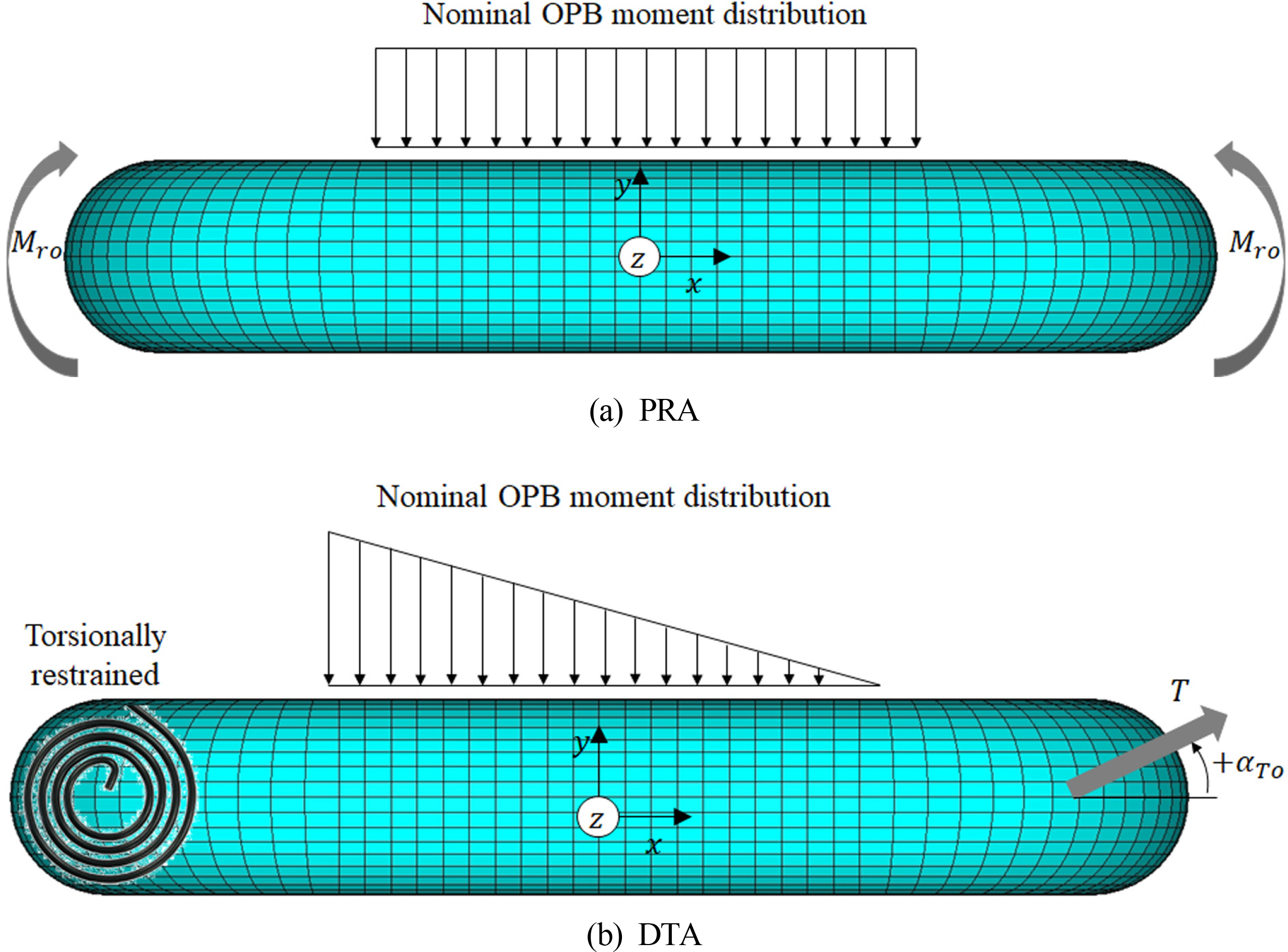
Fig. 2š Š°Çš¡ Š¯š õ¯šÇ ŠÏÚ˜ #3õ°¥ ÚÚÚ š¡šËŠ Ë(T')š ŠÑš˜Ú Ú õ¯š Úš š šÚ Š¯Š Ë Šˆ´ŠˋÚ¡(Reaction moment, MTo)ŠË¥ š Š¯šÚÊŠ Š¯ˋŠýšÇ PRAšÇŠÊ. Š¯Š Ë Šˆ´ŠˋÚ¡Š OPB Šˆ´ŠˋÚ¡š šÈ¥š šÝŠÑšÇŠ₤ŠÀ š (2)š š¯š¡À ŠŠýšÏ¡ ÚÙš šÂ
šÂ
Š˜ÇšŠõ¡¯Š ÚŠÊ. š (2)šš T'Š ŠÏÚ˜ #3š ÚÙš ÚÚÚ õ¯šš š¡šËŠ ˚NJˋ¯, öÝ'ToŠ š¡šËŠ Ë T'š š¡šËõ¯š šŠ₤¡ÚŠÊ.
Choung and Lee(2018)Š 3-ŠÏÚ˜ ÚÇš(Fig. 3(a) š¯¡šÀ¯)š ÚçÚ õ°ŠË šýÇš¡ ŠÏÚ˜š OPB Ú¥ŠÀ Úš šš¡À š š¯´ŠË¥ š šÚšŠÊ(Fig. 4 š¯¡šÀ¯). šÇ š š¯´š šý¨ ŠýšÏ¡Š š šýÇŠšÙÚ ÚÇšš ÚçÚš˜ õ°ŠËš š ššˋÚŠ š¡šËŠ Ë Š¯ š¡šËõ¯š šõ°šÇ Š¯šÇÚ¯ŠË¥ ÚŠ°ÇÚŠ õýšÇŠÊ. šõ°šÇ Š¯šÇÚ¯ŠË¥ Š¯Úš¥ŠÀ š¡šËŠ Ë Š¯ š¡šËõ¯š šçŠõ¯ Š¯ šçšõ¯š ÚŠ°ÇÚŠÊ. š¡šËŠ Ë Š¯ š¡šËõ¯ ŠýšŠË¥ š š Ú õ¯šŠÀ ŠÝŠÑÚš˜ õ¯ ŠÝŠÑš ŠÏŠÊ 3-ŠÏÚ˜ ÚÇšš šÚÚš˜ š¡Ú¯ŠÏÚ˜ õ¯š Š¯ŠË¡ õçÙŠÑ šŠ Ë(Hotspot stress)š š¯š ÚŠÊ. Úçš šçŠ šÈ¥šŠ Ëš õçÙŠÑ šŠ Ëš¥ŠÀ õ¯šÈ¥ÚŠÊ. Fig. 4šš Š
¡Šš š
š 3-ŠÏÚ˜ ÚÇš Š¯ ŠÊšÊ-ŠÏÚ˜ ÚÇš õ°¥š š šŠ₤¡ÚŠÊ. š¡Ú¯ŠÏÚ˜ õ¯š Š¯ŠË¡ õçÙŠÑ šŠ Ëš Fig. 5š 3š¯´šš¥ŠÀ ŠšÚÚšŠÊ. š˜õ¡¯š öÝTiŠ ŠˋÇŠÇ õç§Ú(In-plane bending, IPB) š¡šËõ¯š, Ú šý´š jŠ šÎŠÑ ššŠË¥ šŠ₤¡ÚŠÊ.
3-ŠÏÚ˜ ÚÇšš ÚçÚš˜ š£š õçÙŠÑ šŠ Ëš š¡Ú¯ŠÏÚ˜ õ¯š Ú´ššÇõ¡¯ ŠŠ˜¡š ŠÊšÊ-ŠÏÚ˜ ÚÇšš ÚçÚš˜ š¡Ú¯ŠÏÚ˜ õ¯õ°¥ š¡šËõ¯š õÇõ°ŠË¥ ŠšÑÚ Úšõ¯ šŠÊ. Fig. 3(b)š Š°Çš¡ Š¯š õ¯šÇ Úçš šõ¯ šÇšš ŠÏÚ˜ŠË¥ Ú˜Ú´ÚŠŠÀ ŠÊšÊ-ŠÏÚ˜ ÚÇš Šˆ´Š¡š ššÝÚŠÊ. õ¯ ŠÏÚ˜ š˜šÇš Š¿š Ú šÊÚŠÏ ššŠË¥ Š¯¯š¿Úõ° , 3-ŠÏÚ˜ ÚÇššš š£š OPB õ¯šÝš šÊÚŠÏ ššš Úš õ¯šÝš¥ŠÀ š šÚŠÊ. 3-ŠÏÚ˜ ÚÇššš š£š š¡Ú¯ŠÏÚ˜ õ¯-õçÙŠÑ šŠ Ëš õÇõ°š ŠÊšÊ-ŠÏÚ˜ ÚÇššš š£š š¡Ú¯ŠÏÚ˜ õ¯-š¡šËõ¯š õÇõ°ŠË¥ õý¯ÚˋÚš˜ Š¿ŠÀš š¡šËõ¯-õçÙŠÑ šŠ Ëš õÇõ°õ¯ ššÝŠŠÊ. šÇŠ˜Ú õ°¥š š Fig. 6š š šÚšŠÊ. OPB Šˆ´ŠˋÚ¡š OPB šŠ Ë šÏšÊ õ°š(öÑo)ŠË¥ õ°ÝÚõ° , šÇŠË¥ ŠÏÚ˜š OPB Š´ŠˋÇ õ°š(Zo)ŠÀ ŠŠšÇ õçÙŠÑ šŠ Ëš ŠšÑÚŠ Š¯ˋŠýšÇ š šŠšÇ šŠÊ(BV, 2014). õñ¡Š˜Š õçÙŠÑ šÏš šš šŠ Ë šÏšÊ õ°šŠ š¡šËŠ Ë ŠŠ š¡šËõ¯(š¡Ú¯ŠÏÚ˜ õ¯)š Š¯ŠË¡ Š¿š ښݚ Š°Çš˜šÈ¥Š₤ŠÀ, Š¿š Ú šŠ Ë šÏšÊ õ°šŠË¥ ÚŠ°ÇÚšÏ šŠ Ú õњˊŠ õçÙŠÑ šŠ Ë š¯š ŠýšÇ šŠŠÊ.
šÇŠ₤¡ šÊŠˆ
Ú Š¯š õ¯šÇ, 3-ŠÏÚ˜ ÚÇšš š¡Ú¯ŠÏÚ˜ õ¯-õçÙŠÑ šŠ Ë ŠŠ š¡Ú¯ŠÏÚ˜ õ¯-OPB Šˆ´ŠˋÚ¡ (OPB õ¯šÝ)ŠË¥ ŠšÑÚõ¡¯ šÚš˜ šÚŠŠÊ. 3-ŠÏÚ˜ ÚÇš Šˆ´Š¡š Úçš õ° šýÇ šš(Solid element)ŠÀ õ瘚݊Šˋ¯, šˋšÇÚ š šÇ šÀ¯õÝÇš õç˜Úõ°¥ ŠÏÚ˜ ÚŠˋÇ šŠ Ëš ŠšÑš šÚš˜ õ° šýÇ šš ÚŠˋÇš ŠÏ šŠ Ë šš(Membrane element)ŠË¥ š§Ú
ÚŠÊ.
3-ŠÏÚ˜ ÚÇšš ŠÏÚ˜ #1õ°¥ ŠÏÚ˜ #3š õ¡¡šÇ Š¯ˋÚËš¥ŠÀ Šš¿Ù Šˆ´Š¡š š˜šˋÚŠÊ. Fig. 1šš Š°ÇŠ Š¯š õ¯šÇ õýš˜ ÚšÊ šÊÚ
, õýš˜ ÚšÊ š Ú šÊÚ
, š¡šËŠ Ë šÊÚ
š ŠÏÚ˜š õ¡¡šÇ Š¯ˋÚË ÚšÊšÇŠ₤ŠÀ Šš¥Ú õý§õ° šÀ¯õÝÇšÇ š šˋŠšÏŠÏ, OPB Šˆ´ŠˋÚ¡ šÊÚ
šŠ Š°Šš õý§õ° šÀ¯õÝÇšÇ š šˋŠšÇš¥ ÚŠÊ. 3-ŠÏÚ˜ ÚÇšš š šˋŠŠ õý§õ° šÀ¯õÝÇ Š¯ ÚšÊ šÀ¯õÝÇš š ŠÎ˜Úš˜ Table 1š š šÚšŠÊ.
Fig. 7(b)š Š°Çš¡ Š¯š õ¯šÇ DTAššŠ ŠÏÚ˜ #3š š¡šËõ¯š õ¯šÏŠ š¡šËŠ Ëš õ¯Úš˜ OPB Šˆ´ŠˋÚ¡ŠË¥ š Š¯šÚ´ŠÊ. Š¯ŠˋÇ, PRAš OPB Šˆ´ŠˋÚ¡Š õ¯š Úš š šÚš˜ ššÝŠõ¡¯ ŠŠ˜¡š, šÇŠ šÊš õ瘚À¯Š˜¥ššš OPB Šˆ´ŠˋÚ¡ ššÝ õ¡¯õ瘊À õ¯šÈ¥Šõ¡¯ šÇŠ çŠÊ.
ŠÏÚ˜ #2ššš OPB Šˆ´ŠˋÚ¡ ŠÑÚ˜ŠË¥ šÇšÚÚš˜ Fig. 8š š šÚšŠÊ. šÊš õ°ŠËš šš õ¯š Úš šÇ ššˋÚ š šõ¡¯ ŠŠ˜¡š OPB Šˆ´ŠˋÚ¡Š Fig. 8(b)š õ¯šÇ ŠÑÚ˜Ú õýšÇŠÊ. õñ¡Š˜Š PRAŠË¥ š šˋÚ õý§š¯ Fig. 8(a)š õ¯šÇ OPB Šˆ´ŠˋÚ¡õ¯ ŠÑÚ˜ÚŠÊ. šÇŠ˜Ú šÇš ŠÀ DTAŠ ÚšÊõ°¥ š š˜Ú OPB Šˆ´ŠˋÚ¡ Š¯š õ¡¯õ瘊˥ õ¯šÏŠ õýšÇŠÊ.
š¡šËŠ Ë ŠŠ õ¯š Úš š ŠÏÚ˜ #3š š¯š¡Àš š¯¡šÀ¯ š š (Reference node)š ŠÑš˜ŠŠÊ. šÇŠ š¡šËŠ Ë ŠŠ õ¯š Úš Š°šŠË¥ ŠÏÚ˜ š š š š Š˜Úõ¡¯ šÚš˜ Š°š š£ÊÚŠÏ(Kinematic coupling) ŠŠ ÚšÊ š£ÊÚŠÏ(Distributing coupling)šÇ š šˋŠŠÊ. ÚšÊ š£ÊÚŠÏš ŠÏÚ˜ #3š š¯š¡À Šš¿ÙŠˋÇšÇ ÚŠˋÇš š šÏÚšÏ Šˆ£Úõý ŠŠ˜¡š õњˊšÏ šŠŠÊ. Š°š š£ÊÚŠÏš š˜šˋÚ õý§š¯ šš š¡ šÊÚ
õ°¥ OPB Šˆ´ŠˋÚ¡ šÊÚ
š š šˋŠŠ š¯¡šÀ¯ š š õ°¥ šÂ
š š š š˜šÇš šÂ
ššÝ(Dependency)šÇ šŠÀ ŠÊŠËÇõ¡¯ ŠŠ˜¡š, ÚÇš ŠšÊ Šˆ´Š¡š Š°õý§ÚŠ õ° Šš šš¿ ÚÇš õ¡¯ŠýšÇ šõ瘊ŠÊ. Choung and Han(2016a)š Choung and Han(2016b)Š š Ú ÚšÊ šÊÚ
š Š°š, šŠ Ë, Š°ÚŠË ŠÝš š Š°ÇŠÏš ÚÚ šÊÚ
šš ššŠ¯š šŠÀšÇ Š°š š£ÊÚŠÏ šÂ
š šÀ¯õÝÇš š šÚŠ õ¡¯Šýš š šÚ Š¯ šŠÊ.
šõ¯ ššÙ š šýÇŠŠ ËÚ ÚÇšš¥ŠÀŠÑÚ¯ š¡šËŠ Ë šÇŠ Ë Š¯ š¡šËõ¯ šÇŠ Ë, 3-ŠÏÚ˜ ÚÇšš¥ŠÀŠÑÚ¯ OPB õ¯šÝš š£š Ú, š¡šËõ¯-OPB Šˆ´ŠˋÚ¡ õÇõ°ŠË¥ ŠšÑÚõ¡¯ šÚš˜ ŠÊšÊ-ŠÏÚ˜ ÚÇššÇ šõ瘊ŠÊ. Fig. 3(b)š Š°Çš¡ Š¯š õ¯šÇ, š ÚÚŠ š¡Ú¯ŠÏÚ˜ õ¯ŠŠ ÚÚÚŠ š¡Ú¯ŠÏÚ˜ õ¯ŠŠ°ÇŠÊ Ú˜ŠÊ. šŠË¥ ŠÊšÇ mõ¯š ŠÏÚ˜õ¯ šŠÊŠˋÇ, öÝinto1 > öÝinto2 > öÝinto3...> öÝ(into(m-1)š õÇõ°õ¯ šÝŠÎ§ŠŠÊ. öÝ(into(m-2) ã öÝ(into(m-1)šŠÏšÀÝÚŠŠÀ šÑˋŠÑÚ ŠÏš ŠÏÚ˜š õ¯šõ¯ ŠÊšÊ-ŠÏÚ˜ ÚÇšš š˜šˋŠšÇš¥ ÚŠÊ. BV(2014)š šÚŠˋÇ 20õ¯ šÇšš ŠÏÚ˜ŠË¥ š˜šˋÚ õýš õÑšËÚŠÊ.
ŠýÊš¿ŠÏÚ˜ šÊÚ¯ŠŠË¥ šÚš˜ 8MWõ¡ ÚÇš ÚŠ Ë Š¯š õ¡¯š š˜šˋŠ õ°ŠËš š Ššš¥ŠÀ š šˋÚšŠÊ(Li et al., 2018). ÚÇš ÚŠ Ë Š¯š õ¡¯ Úšš Fig. 9š õ¯ŠÊ. šÇŠÊšÇ š˜šˋÚ ŠÏÚ˜š Ú¡š¿Ù šÏŠÎ(Nominal diameter)š 100mm(D100)šš¥Š, Š°¡ š¯õ瘚šŠ 107mm(D107)ŠÀ õ¯š ÚšŠÊ. ŠÚ ŠÏÚ˜š šš˜ ŠÝõ¡š R4šŠÊ. Ú¡š¿ÙšÏŠÎõ°¥ ŠÝõ¡š šÇšˋÚš˜ õýš˜ ÚšÊ(Ppf), šçš ÚŠ´ ÚšÊ(Pmbl), Š´š õ¡¡šÇŠ¿ šÑ õ¯šÝ(Axial stiffness, Ka)š Table 1š š šÚšŠÊ(DNV, 2010). ŠÚ Table 1š š šŠ õ¯Š õ°š(K)š õ¯õ°ç õý§Úõ°š(n)ŠË¥ õ°šŠÀ õ¯šÏŠ ŠˋÝ Šýš¿(Power law)ŠË¥ šÇšˋÚš˜ šš˜š š Š šŠ Ë(Flow stress)ŠË¥ š šÚšŠÊ.
Fig. 3(a) Š¯ Fig. 7š š šŠ õ瘚À¯ ÚÇš Šˆ´Š¡š ŠýÊš¿ ŠÏÚ˜ šÊÚ¯Šš 3-ŠÏÚ˜ ÚÇšš š šˋÚšŠÊ. ššˋ ÚÇš ÚŠÀõñ¡Š´ ABAQUS V6.8š šÇšˋÚš˜ 3-ŠÏÚ˜ ÚÇššÇ šÚŠšŠÊ. õç§Úš ŠÚ Š¿š ÚˋšÝš õ¯š Ú 8ŠˋÇšýÇ õ¯š¯´ š ŠÑ õ° šýÇ šš(C3D8RI)ŠË¥ šÇšˋÚš˜ ŠÏÚ˜ŠË¥ Šˆ´Š¡ŠÏÚšŠÊ. ŠÏÚ˜ ÚŠˋÇššš š ŠÂ¯šÝ šŠ šŠ Ë ÚŠ°Çš ŠÏÚ˜ õ¯ šˋšÇÚ š šÇš õç˜ÚÚõ¡¯ šÚš˜, Š˜ÇšÚ ŠÏÚ Šõ£ŠË¥ õ¯šÏŠ õ¯š¯´ š ŠÑ ŠÏ šŠ Ë šš(M3D4R)ŠË¥ ŠÏÚ˜ ÚŠˋÇš š§Ú
ÚšŠÊ. 3Šý ŠÏÚ˜š š¯š¡Àš šš¿Ú š¯¡šÀ¯ š š õ°¥ ŠÏÚ˜š Š´ŠˋÇš Š¯¯š¿Š šÂ
š š š š Š°š š£ÊÚŠÏ ššŠÀ õý¯ÚˋÚšŠÊ. šÇŠ 1Šý šÊÚ
ŠÑÚ¯ 3Šý šÊÚ
õ¿šÏš š¯¡šÀ¯ š š õ°¥ šÂ
š š š š˜šÇš x-ÚŠˋÇ Šš¿Ù šÂ
ššÝš ŠÑš˜ÚšŠÊ. Š¯ŠˋÇ ŠÏšÏŠÏ ÚšÊ šÊÚ
(OPB šÊÚ
)šš šš õ瘚 šÂ
ššÝš ŠÑš˜ÚšŠÊ(Choung and Han, 2016a; Choung and Han, 2016b; Choung and Lee, 2018). 3-ŠÏÚ˜ ÚÇšš šÚš˜ š šˋŠ šš õ¯šŠË¥ Table 2š š ŠÎ˜ÚšŠÊ.
3-ŠÏÚ˜ ÚÇšš šý¨ŠýšÏ¡ šÊÚ
š Table 1š š šŠ Ppfõ¯ š šˋŠšš¥Šˋ¯, ŠŠýšÏ¡ šÊÚ
šš Ppfõ¯ š õݯŠšŠÊ. š¡ŠýšÏ¡ šÊÚ
šš šÊš š¡šËŠ Ë(T)šÇ š¯¡šÀ¯ š š š ŠÑš˜ŠšŠÊ. 3-ŠÏÚ˜ ÚÇš õý¯õ°¥Š š¡šËŠ Ëõ°¥ š¡šËõ¯š Ú˜õ¡¯š Š¯Š¥ Š°Šš šÇŠÊ. šÊš š¡šËŠ Ëš Ú˜õ¡¯Š Pmblš šÇõ°¥Ú š ššÏŠÏ, õ°ŠËš š ššˋÚŠ š¡šËŠ ËšÇ 0.5 Pmblš šÇõ°¥ÚšÏ šŠŠÀ šš š´š õ¯šÏŠŠÀ šÊõ°ÚŠ õýšÇ š¥Š¯š šÇŠÊ. Š°¡ š¯õ瘚šŠ T = 0.1Pmbl, 0.3Pmbl, 0.5Pmblš õ°ŠË šýÇš¡ ŠÏÚ˜š ššˋÚŠ š¡šËŠ Ëš¥ŠÀ õý¯š ÚšŠÊ. ŠÊ ŠýšÏ¡ šÊÚ
šš OPB šý¨ ŠýšÏ¡ š¡Ú¯ŠÏÚ˜ õ¯(öÝinto1)šÇ 5Š šÇš Š¯šÚŠŠÀ š¡šËõ¯š ŠÑš˜ÚšŠÊ. õ¯ šÊÚ
Š°ŠÀ š šˋÚ õý§õ° šÀ¯õÝÇš Table 3š š ŠÎ˜ÚšŠÊ. ÚÇš šÊÚ šÀ¯õÝÇš õ¯šÚš˜ ŠÏÚ˜ õ¯š ŠÏš¯¯ õ°š ö¥=0.3š š šˋÚšŠÊ(BV, 2014).
ŠÏÚ˜ #2š šÊšŠÑ Š´ŠˋÇš šŠ Ëš ššÑõ°¥ š¡šËš¥ŠÀ ŠŠšÇ Fig. 10š š šÚšŠÊ. 0.5Pmblš š¡šËŠ Ëš š šˋÚš õý§š¯ šŠ ËŠÑÚ˜Š Fig. 10(a)š õ¯ŠÊ. õýš˜ ÚšÊ š Ú Úš šÊšŠÑ Š´ŠˋÇš š šýÇš š¥ŠÀ Š´ššŠ ššÑ šŠË šŠ ËšÇ š¡šËŠ Ëš šÚš˜ ŠŠÑŠÑ š¡šË šŠ Ëš¥ŠÀ Š°Úõ° , Š´ŠˋÇ š¡õ°§ š¥ŠÑš ššÑ šŠ ËšÇ ššÀÇÚŠ õýš Fig. 10(a)šš Úš¡šÇ õ¯ŠËÚŠÊ. šš š¡šËŠ Ë ššˋÚ Š ŠÏÚ˜ #2š ÚÚŠÑõ¯ ššˆ§š¥ŠÀ õ¯õ¿ššÏŠ Š¯ˋÚË(z-Š¯ˋÚË)š¥ŠÀ Š°ÚÚõ¡¯ ŠŠ˜¡š, Š´ŠˋÇ š¡õ°§š ššÑ šŠ ËšÇ šÀÇš˜ÚŠ õýš¥ŠÀ šÑš ŠŠÊ.
DTAš õ¡¯Š¯Ú OPB Šˆ´ŠˋÚ¡ŠË¥ ššˋšÚ˜ õý§š¯ ŠÏÚ˜ #2š ššÑšŠ Ë ŠÑÚ˜Š Š¿õçš š õý Š°ÚŠ õýš Fig. 10(b)ŠÀŠÑÚ¯ Úš¡šÇ õ¯ŠËÚŠÊ. Š¯ŠˋÇ, PRAš õ¡¯Š¯Ú OPB Šˆ´ŠˋÚ¡ŠË¥ ššˋšÚ˜ õý§š¯ ŠÏÚ˜ #2š y-Š¯ˋÚË ÚŠÑõ¿šÏ ššÑ šŠ ËšÇ Š¯Š˜ÚŠ õýš Fig. 10(c)šš Úš¡Ú š šŠÊ. šÇŠ ÚÇš Š¯ˋŠýš Š¯Š¥š ŠÏÚ˜ #2 šŠ Ëš ŠÑÚ˜õ¯ Ú˜õý Š°Šš šÇŠ¥Š šÎõݯšÇŠÊ.
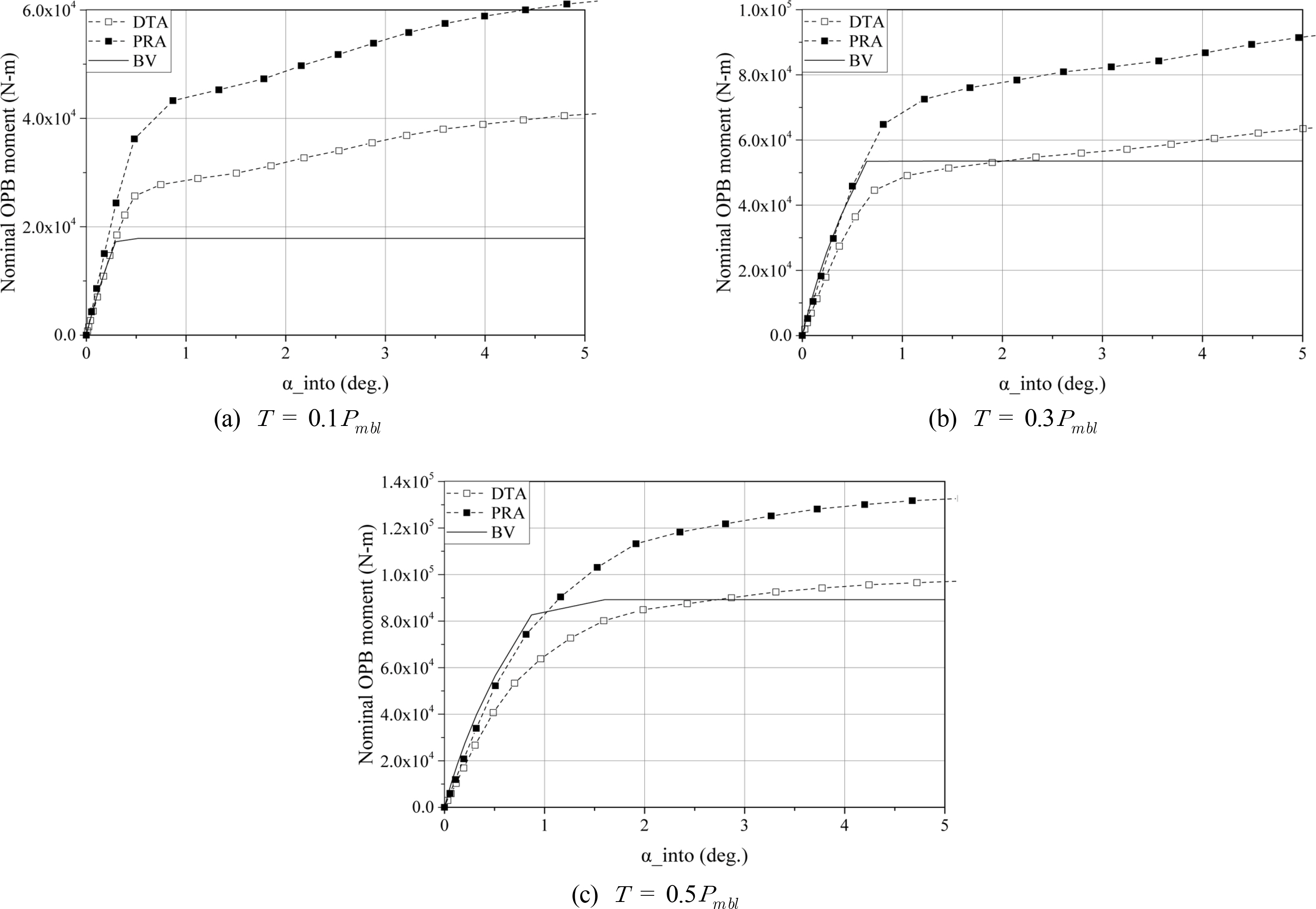
Fig. 11(a), (b), (c)Š õ¯õ¯ Pmblš 10%, 30%, 50%ŠË¥ š¡šËŠ Ëš¥ŠÀ ššˋšÚ˜ Š, DTA, PRA, BV õ¯šÇŠŠ¥š¡š šÇšˋÚš˜ õ°š¯Š OPB õ¯šÝš ŠÚŠ¡ŠÊ. šÇŠ š šˋÚ BV õ¯šÇŠŠ¥š¡š š (3)š š ŠÎ˜Úš˜ ŠÚŠŠÊ. š¡šËŠ ËšÇ õ¯šË šš Š(0.1Pmbl)ŠË¥ š š¡Úõ° , DTA õ¡¯Š¯ OPB õ¯šÝšÇ BV õ¯šÇŠŠ¥š¡ õ¡¯Š¯ õý¯õ°¥š Š¿õçš š š˜Ú õýš Úš¡Ú š šŠÊ. Š¯ŠˋÇ PRA õ¡¯Š¯ OPB õ¯šÝš š¡šËŠ Ë Ú˜õ¡¯š õÇõ°ššÇ Ú˜õý šš¡ÀŠšŠÊ. BV õ¯šÇŠŠ¥š¡š šÚ õ瘚Šˆ´Š õ¯šÝ(Locking mode stiffness)Š PRA õ¡¯Š¯ õý¯õ°¥š šŠ¿Ú š¥š¿ÚŠ õý§ÚËš ŠÚŠ¡ŠÊ. š (3)š õý§Úššš õ¯šÚ Š PRA õ¡¯Š¯š¥ŠÀ ŠšÑŠšš õýš¥ŠÀ šÑš ŠŠÊ. ŠÚ š (3)š õ¡¯Š¯Ú Š₤¡ŠŠÎ¥ Šˆ´Š õ¯šÝš š¡šËŠ Ë Ú˜õ¡¯š õÇõ°ššÇ 0š šŠ ÇÚŠ õýš Úš¡Ú š šŠÊ. Š¯ŠˋÇ PRA Š¯ DTA õ¡¯Š¯ Š₤¡ŠŠÎ¥ õ¯šÝš Š˜ÇšÚ š šõ° , ŠšÝšÇ õ瘚 Šˆ´Ššš Š₤¡ŠŠÎ¥ Šˆ´ŠŠÀš šýšÇŠË¥ Šˆ
ÚÚõý õ瘊ÑÚ š šŠÊ. šÇŠ˜Ú õý§ÚËš ŠÛš š¡šËŠ Ëšš Š ŠŠ ñÚŠÊ. ŠÛš š¡šËŠ Ëšš ŠÏš¯¯š šÚ õ瘚Š ËŠ šõ¡¯ ŠŠ˜¡š šÇ õý§ÚËš Š˜¥ŠÎ˜š š¥ŠÀ ÚŠ¿Ú õý¯õ°¥ŠÀ š˜ŠÈŠŠÊ.
where
P(öÝinto)=öÝinto+0307öÝ i n t o 3 öÝ i n t o 5
a(öÝinto)=0.439+0.532tanh(1.02öÝinto)
b(öÝinto)=0.433-1.640tanh(1.32öÝinto)
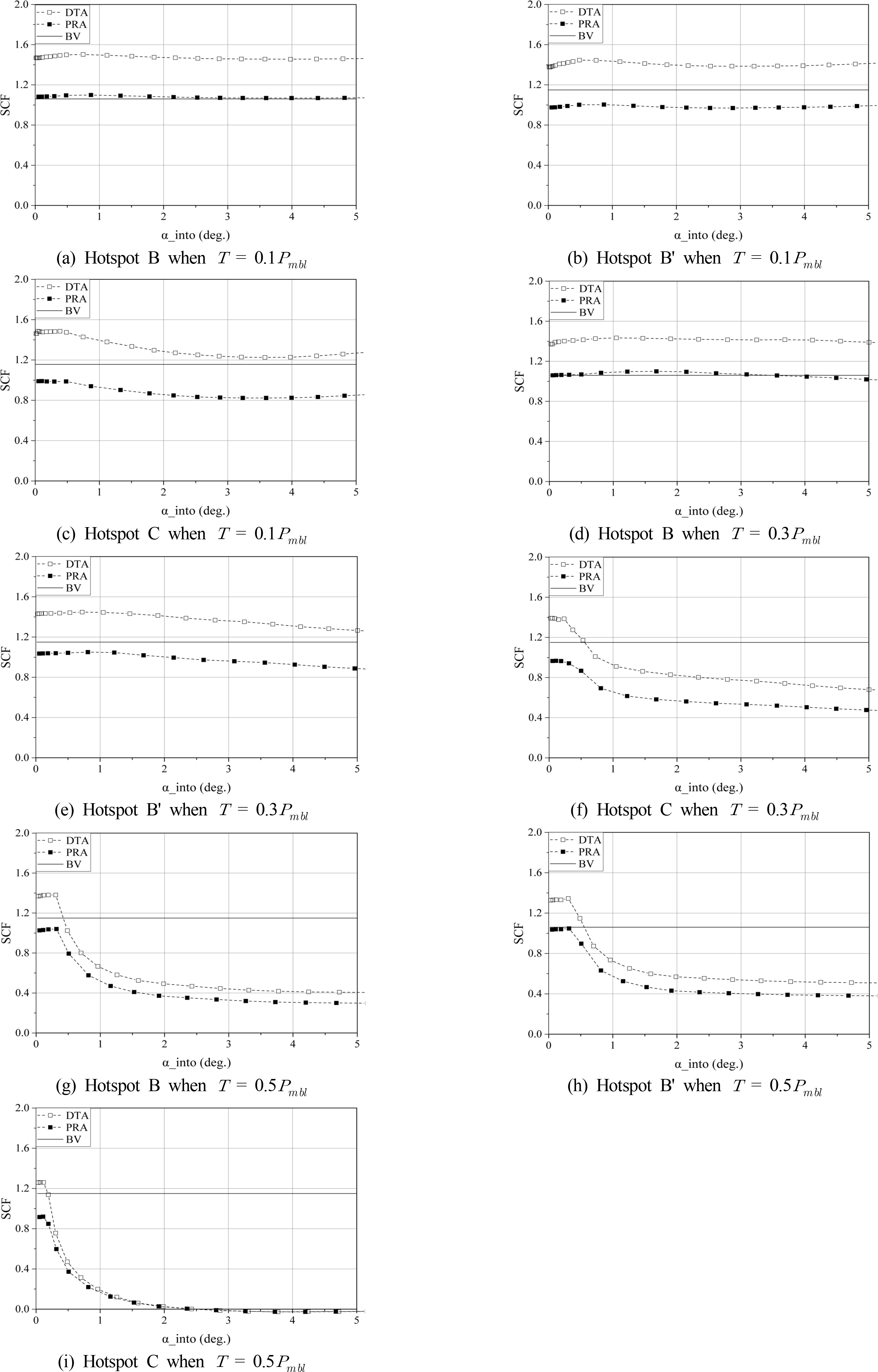
BV õ¯šÇŠŠ¥š¡šÇ š šÚŠ 3õ¯š õçÙŠÑ šÏš (B, B', C)š Fig. 12š ŠÚŠÇšŠÊ(Rampi et al., 2015). 3õ¯š õçÙŠÑ šÏš š ŠÚ õçÙŠÑ šŠ Ëõ°¥ š¡Ú¯ŠÏÚ˜ õ¯š õÇõ°ŠË¥ 3-ŠÏÚ˜ ÚÇšš¥ŠÀŠÑÚ¯ ŠšÑÚšš¥Šˋ¯, šÇŠË¥ Fig. 13š š šÚšŠÊ. š¡šËŠ Ë ššÊšÇ 0.1Pmblš¥ Š BV õ¯šÇŠŠ¥š¡š õçÙŠÑ šŠ Ëš šŠ¿Ú õ°¥š Úõ¯Úõ° ššš Figs. 13(a)-13(c)ŠÀ ŠÑÚ¯ Úš¡Ú š šŠÊ. ŠÏÚ˜ #1õ°¥ õ¯šË õ¯õ¿šÇ õçÙŠÑ šÏš š CšÇŠˋ¯, šÇ šÏš ššš DTA õ¡¯Š¯ õçÙŠÑ šŠ Ëš PRA õ¡¯Š¯ õçÙŠÑ šŠ Ëõ°¥ šŠ¿Ú š¥š¿ÚŠ õýš Fig. 13(c)ŠÀŠÑÚ¯ Úš¡Ú š šŠÊ.
š¡šËŠ ËšÇ 0.3PmblŠÀ šÎõ¯ÚŠˋÇ šÊÚŠ Ê BV õ¯šÇŠŠ¥š¡šÇ õçÙŠÑ šŠ Ëš õ°¥š Úõ¯Úõ° ššš Fig. 13(f)ŠÀŠÑÚ¯ Úš¡šÇ õ¯ŠËÚŠÊ. š¡šËŠ ËšÇ 0.5PmblŠÀ šÎõ¯ÚŠˋÇ BV õ¯šÇŠŠ¥š¡ õ¡¯Š¯ õçÙŠÑ šŠ Ëš DTA õ¡¯Š¯ õçÙŠÑ šŠ Ë ŠŠ PRA õ¡¯Š¯ õçÙŠÑ šŠ Ëš Š¿Úš˜ ššýÙŠõý Ú˜ŠÊŠ š˜šÊš Úš¡Ú š šŠÊ(Figs. 13(g)-13(i) š¯¡šÀ¯). Š¯ŠˋÇ š¡šËŠ Ëš šÎõ¯š Š¯Š¥ DTAš PRAš šÚ õçÙŠÑ šŠ Ëš šŠÀ š¥š¿ÚŠ õýš Úš¡Ú š šŠÊ.
Fig. 13š š šŠ õçÙŠÑ šŠ Ëš ŠÏÚ˜ #2š Š´ŠˋÇ õ°šŠË¥ õ°ÝÚõ° šÇŠË¥ OPB Šˆ´ŠˋÚ¡ŠÀ ŠŠŠˋÇ š (4)š õ¯šÇ OPB šŠ Ë šÏšÊ õ°š öÑo (Stress concentration factor, SCF)ŠË¥ ŠšÑÚ š šŠÊ. ÚššÝ ÚÇšš Š¿š ÚšÝ Š¯ š šÇ Š˜¡š š Š¿š ښݚ õ° Š ÊÚŠˋÇ öÑoŠ Š¿š Úš¥ŠÀ šš¡ÀŠŠÊ. šÇŠË¥ õÇš¯¯Úõ¡¯ šÚš˜ Fig. 14š öÑoŠË¥ š šÚšŠÊ. ŠÛš ÚšÊ(0.1Pmbl)šš õçÙŠÑ šÏš š õÇõ°ššÇ Š¿õçš š¥š Ú šŠ Ë šÏšÊ õ°šõ¯ š šÏŠŠ õýš Úš¡Ú š šŠÊ(Figs. 14(a)-14(c) š¯¡šÀ¯). Š¯ŠˋÇ š¡šËŠ ËšÇ 0.3PmblŠÀ šÎõ¯Ú õý§š¯, ŠÏÚ˜ #1š õ¯šË õñ¥š Ú õçÙŠÑ šÏš š¡ Cšš SCFŠ šŠ¿Ú Š¿š ښNJÊ. š¡šËŠ ËšÇ 0.5PmblŠÀ šÎõ¯Ú õý§š¯, õçÙŠÑ šÏš š õÇõ°ššÇ šÇõ¡¯ SCFŠË¥ š šÏÚšÏ Šˆ£Úõ° š¡Ú¯ŠÏÚ˜ õ¯šÇ šÎõ¯ÚŠˋÇš SCFõ¯ õ¡õýˋÚ õ¯šÚŠ Úšš õÇš¯¯Ú š šŠÊ. OPB Šˆ´ŠˋÚ¡Š õƒ¡šÊÚ šÎõ¯ÚŠŠ¯ Š¿ÚÇ, OPB õçÙŠÑ šŠ ËšÇ õ¡õýˋÚ õ¯šÚÇš Š¯šÚ ÚššÇŠÊ. BV õ¯šÇŠŠ¥š¡š õçÙŠÑ šÏš š Š¯ŠË¡ SCFŠË¥ š õ°çÚõ° ššÏŠÏ, š¡Ú¯ŠÏÚ˜ õ¯š Š¯Š¥ Š°ŠÚŠ SCFŠË¥ š õ°çÚšÏ šŠŠÊ. šÇŠ˜Ú šÇš ŠÀ š¡Úš˜ BV õ¯šÇŠ Š¥š¡š š¡šËŠ ËšÇ šÎõ¯Úš Š õçÙŠÑ šŠ Ëš õ°¥Š Úõ¯ÚŠÊõ° šÑš ŠŠÊ.
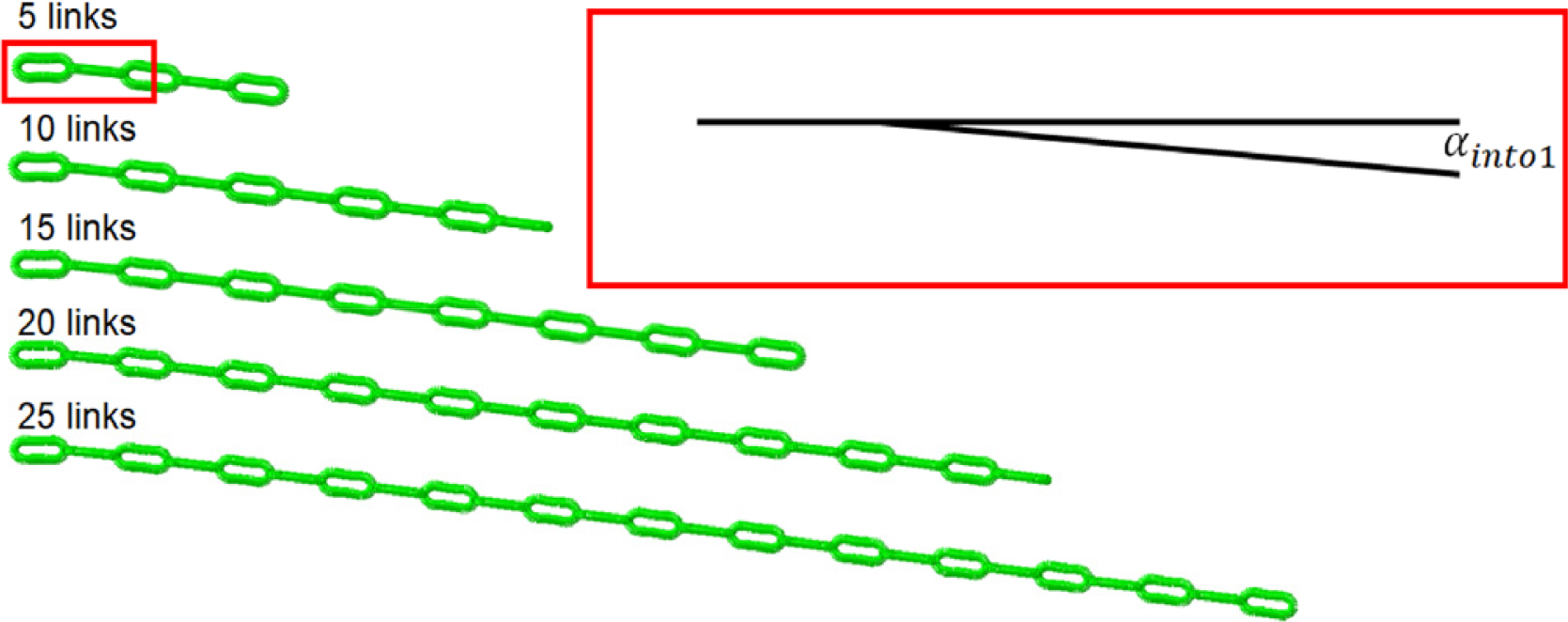
Fig. 3(b)š š šŠ õ瘚À¯ ÚÇš Šˆ´Š¡š ŠÚ ŠÏÚ˜ õ¯š Úõ¯ŠË¥ šÊšÚšŠÊ. ŠÊšš 3š¯´š Š°Ç šš(B31)ŠË¥ šÇšˋÚš˜ 1õ¯ ŠÏÚ˜š õ¡¯ÚÚš Úšš šçŠÚ õç˜ÚÚšŠÊ. ŠÏÚ˜ 1õ¯Š¿ š˜šˋÚ Š°Ç ššš õ¯šŠ šÏš ŠÑ 4õ¯, ŠÏõ°ÀŠÑ 16õ¯, šÇ 20õ¯šÇŠÊ. 3-ŠÏÚ˜ ÚÇšš š šˋŠ š˜ŠÈ ššÝš ŠÊšÊ-ŠÏÚ˜ ÚÇšš š šˋÚšŠÊ. ŠÏÚ˜õ¯ ŠÏŠŠ š š š Úš šš ŠŠË¥ š õݯښ˜ ŠÏÚ˜õ¯ Úš šÇ õ¯ŠËÚŠŠÀ ÚšŠÊ. šÇÚ ŠÏÚ˜õ¯ ŠÏŠŠ š š š šÊÚŠÏ ššŠË¥ Š¯¯š¿Úõ° Fig. 11š š šÚ DTA õ¡¯Š¯ OPB õ¯šÝš ŠÑš˜ÚšŠÊ. ŠÊšÊ-ŠÏÚ˜ ÚÇšš š šˋŠ õý§õ° šÀ¯õÝÇš 3-ŠÏÚ˜ ÚÇšš š šˋŠ õý§õ° šÀ¯õÝÇõ°¥ Šš¥ÚŠÊ. šÇŠ š šˋÚ š¡šËŠ Ëš T = 0.5PmblšÇŠˋ¯ š¡šËõ¯š öÝTo = 1.5ô¯šÇŠÊ. Š°¡ š¯õ瘚šŠ ŠÏÚ˜š õ¯šŠË¥ õý¯š Úõ¡¯ šÚš˜ Fig. 15š õ¯šÇ 5šÂ
ŠËš ŠÏÚ˜ õ¯š(5õ¯, 10õ¯, 15õ¯, 20õ¯, 25õ¯)ŠË¥ šÊŠ¿ÚšŠÊ. ššˋ ÚÇš ÚŠÀõñ¡Š´ ABAQUS V6.8š šÇšˋÚš˜ ŠÊšÊ-ŠÏÚ˜ ÚÇšš šÚÚšŠÊ.
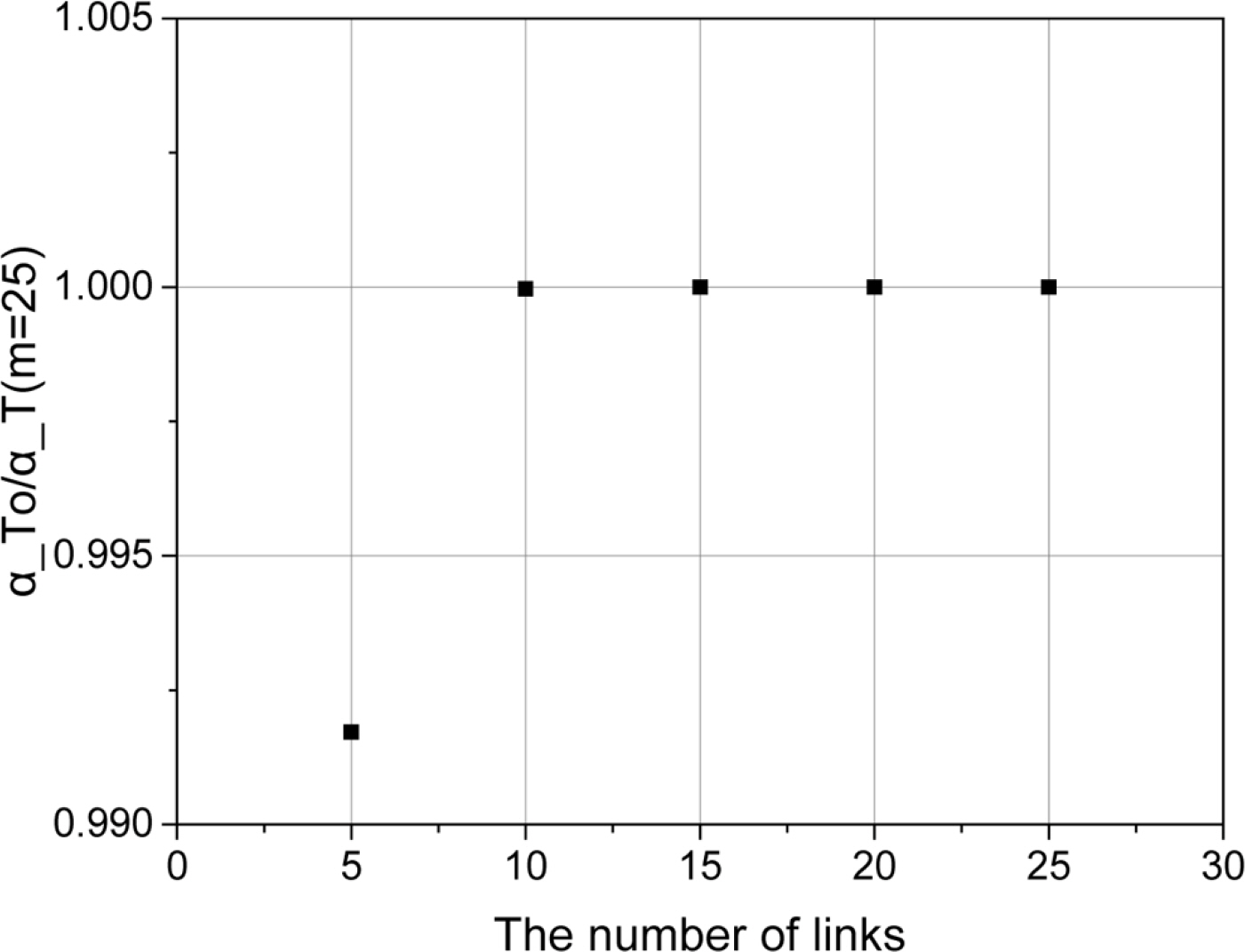
Fig. 16š ŠÏÚ˜š õ¯šš Š¯ŠË¡ Š˜Çš¯´š öÝinto1(šý¨ ŠýšÏ¡ š¡Ú¯ŠÏÚ˜ õ¯)šÇŠÊ. ŠÏÚ˜š õ¯šõ¯ 25õ¯(m=25)š¥ Šš öÝinto1ŠË¥ š Šçš¥ŠÀ õ¯šÈ¥Úõ° ŠÏÚ˜ õ¯šš Š¯ŠË¡ öÝinto1ŠË¥ Š˜Çš¯´šÚš˜ Fig. 16š š šÚšŠÊ. ŠÏÚ˜š õ¯šõ¯ 10õ¯ šÇšš¥ õý§š¯ šŠ ÇÚŠ öÝinto1š š£š š ššš¥Šˋ¯, Š¯Š¥š ŠÊšÊ-ŠÏÚ˜ ÚÇšš š šˋŠŠ ŠÏÚ˜š šçš õ¯šŠ 10õ¯ŠÀ š šÚŠÊ.
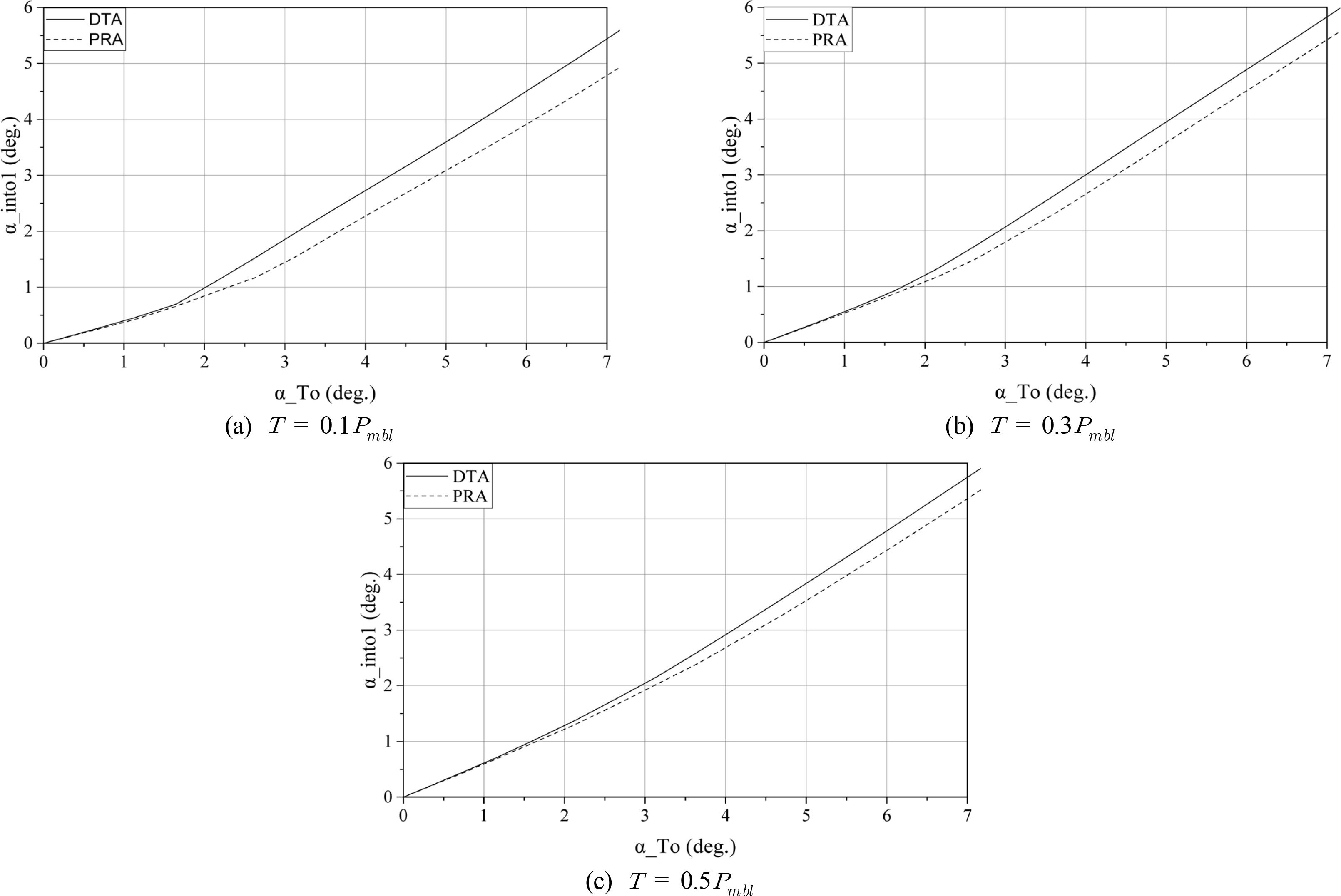
ŠÏÚ˜š õ¯šŠË¥ 10õ¯ŠÀ ŠÊšÊ-ŠÏÚ˜ ÚÇšš šÚÚ Ú š¡šËõ¯(öÝTo)õ°¥ šý¨ ŠýšÏ¡ š¡Ú¯ŠÏÚ˜ õ¯(öÝinto1)š õÇõ°ŠË¥ š ŠÎ˜Úš˜ Fig. 17š š šÚšŠÊ. šš¡ÀÚŠŠÀ DTA õ¡¯Š¯ OPB õ¯šÝš š šˋÚ öÝTo-öÝinto1š õÇõ°Š PRA õ¡¯Š¯ öÝTo-öÝinto1š š¯´šÇŠË¥ Š°ÇšŠÊ. 3-ŠÏÚ˜ ÚÇšŠýš õçÙŠÑ šŠ Ë Úõ¯šŠ šÚËš Š₤¡š¿ Š¢ŠÏ šŠŠ¥, ŠÊšÊ-ŠÏÚ˜ ÚÇššŠ šÚËš Š₤¡š¿ŠÊŠ šÎõݯšÇŠÊ.
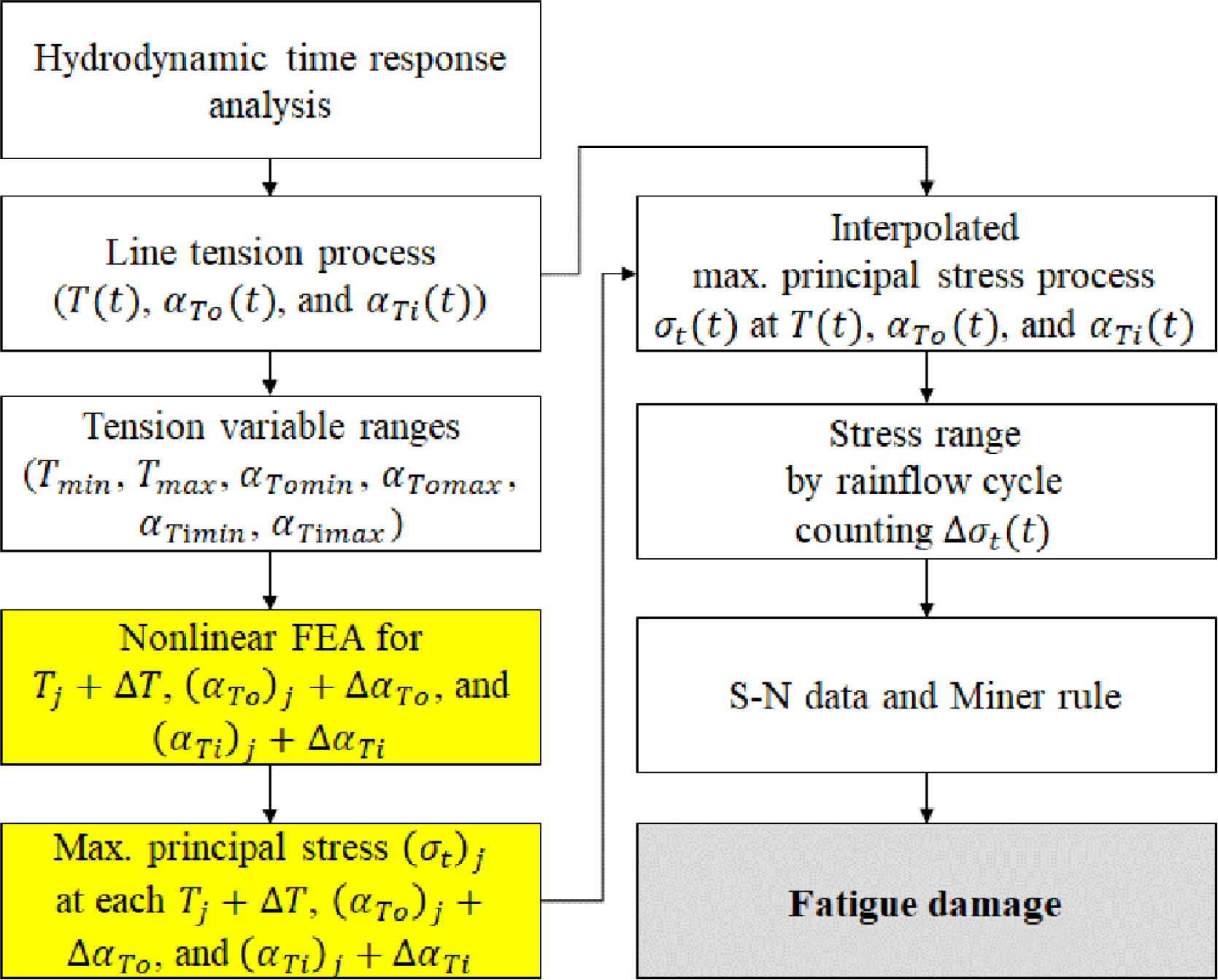
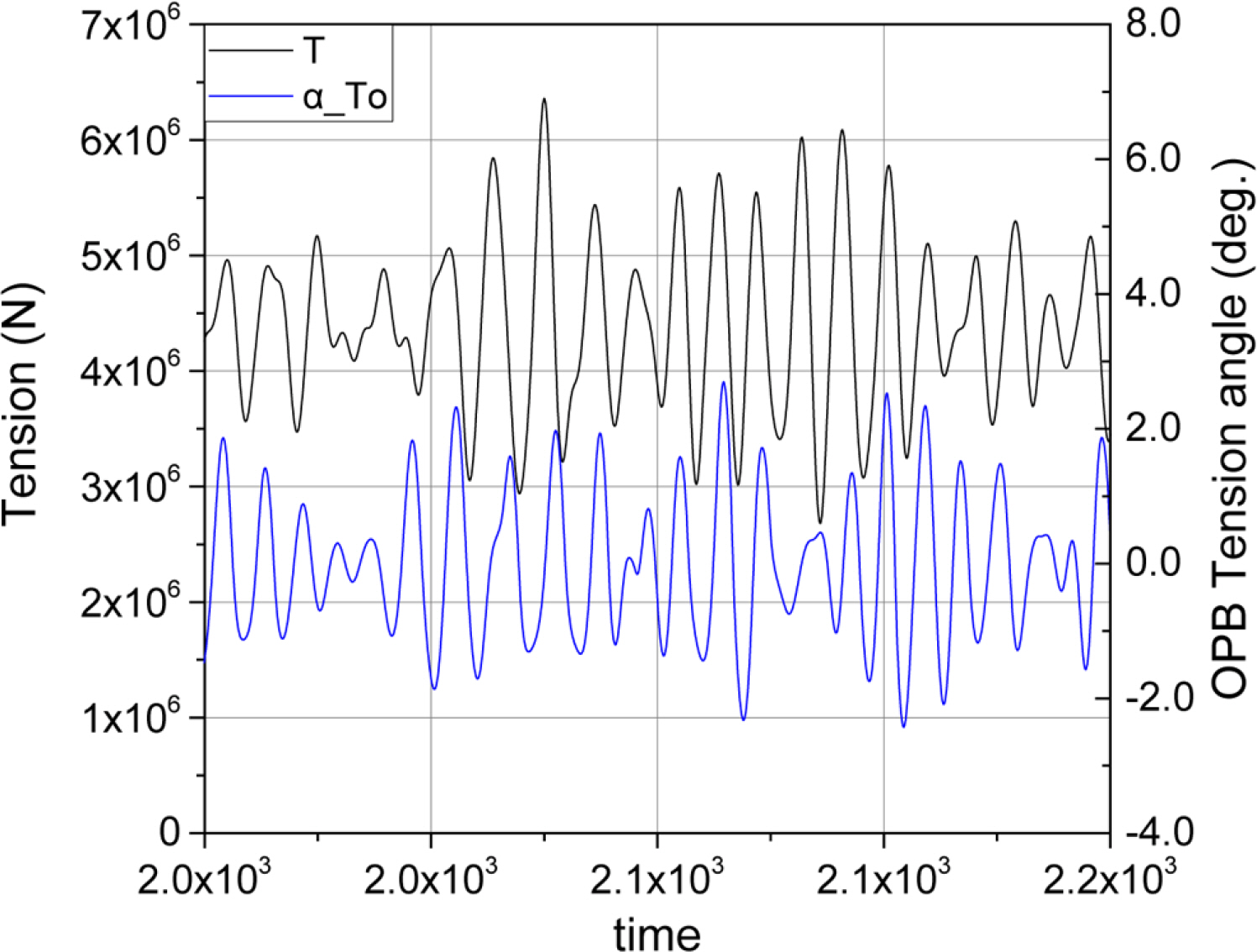
OPBŠË¥ õ° Š ÊÚ Šš Ú¥ŠÀŠË¥ š¯š Úõ¡¯ šÚÇšŠ Fig. 4š š šŠ š š¯´ŠË¥ Š¯Š¥š¥ ÚŠÊ. šÎ š šýÇŠšÙÚ ÚÇšš ÚçÚš˜ š¡šËŠ Ëš šÇŠ Ëõ°¥ š¡šËõ¯š šÇŠ Ëš š£šÇš¥ ÚŠÊ. Fig. 18š Fig. 9š š šÚ ÚŠ Ë Š¯š õ¡¯š šõ¯ šŠç ÚÇšš ÚçÚš˜ š£š 1Šý õ°ŠËš š š¡šËŠ Ë šÇŠ Ëõ°¥ š¡šËõ¯ šÇŠ Ëš ŠÚŠ¡ŠÊ. š¡šËŠ Ëš Úõñ õ¯š šš šÇõ¡¯ š¡šË(Pre-tension)õ°¥ šÀ¯ŠË ŠÝš šÚš˜ Š¯šÚ ÚÙŠ Ëš šÚ š¡šËŠ Ëš Ú˜Ú´ÚŠÊ.
õñ¿Ú ښʚ õÇš šš š¡šËŠ Ëš Úõñ õ¯š ŠÏÊš¯ šÊšÚŠÊ. Š¯ŠˋÇ, š¡šËŠ Ë-šŠˆ
š Š ŠŠ šŠ Ë-šŠˆ
š ŠŠ šŠ Ë Š¿ ŠŠ ÚšÊ Š¿õ¯ 0šÇ ŠŠŠÀ šÊÚÚš˜ š£š õýšÇŠ₤ŠÀ, Úõñ š¡šËŠ Ë ŠŠ Úõñ šŠ Ëš Ú´õ°¥õ¯ šÇŠ₤¡ š¡šËŠ Ë-šŠˆ
š Š ŠŠ šŠ Ë-šŠˆ
š Šš Ú˜Ú´Š õýš¥ŠÀ õ¯šÈ¥ÚŠÊ. šÇŠ˜Ú šÇš ŠÀ Ú¥ŠÀš õÇš šš š¡šËŠ Ëš ŠýšŠÏš š˜šˋÚŠˋ¯, Rainflow šÏõ°Šýš šÇšˋÚš˜ š¡šËŠ Ëš ŠýšŠË¥ šÏõ°Ú š šŠÊ.
Fig. 18š š šŠ š¡šËõ¯š ŠÑš šýÇš šÇŠ šÇŠ Ëõ°¥ š¡šËŠ Ëš šÇŠ Ëš Ššš õ° Š ÊÚš˜ ššÝŠšÇš¥ ÚŠÊ. šÎ ښNJΘŠ ŠŠ šýÇš¡ Ú¡šÊ ŠÝšÇ š˜šˋŠ õý§š¯, ŠÑš šýÇš šÇŠš õ° Š ÊÚ OPB š¡šËõ¯š Úõñ õ¯š ÚÙš 0š õ¯šÏŠŠÀ š õñÚŠšÇš¥ ÚŠÊ. Fig. 18š š šŠ š¡šËõ¯š Úõñ š 0šš šÏõÇš š¥ŠÀ š š šŠÊ.
OPB Šˆ´ŠˋÚ¡š Š¯š õ¡¯õ瘊˥ šÊŠˆ
Úšš¥Šˋ¯, PRAš DTAš õ¡¯Š¯Ú 3-ŠÏÚ˜ ÚÇšš ŠÚš˜ šõ¯ÚšŠÊ. ŠÚ 3-ŠÏÚ˜ ÚÇš Š¯ ŠÊšÊ-ŠÏÚ˜ ÚÇšš õ° Š ÊÚ OPB Ú¥ŠÀ ÚÇš š š¯´š ŠÚš˜ šõ¯ÚšŠÊ. PRAš DTAš õ¡¯Š¯Ú 3-ŠÏÚ˜ ÚÇšš š¯´šÇš š ŠÚš˜ šš¡Ú šõ¯ŠË¥ ÚšŠÊ. Ú¿Ú OPB Šˆ´ŠˋÚ¡š ŠÑÚ˜ŠË¥ Š¿õçÚš˜(šõ¡¯) Š Š¯ˋŠýš š¯´šÇš š Úš¡ÚšŠÊ. ŠÊšÊ-ŠÏÚ˜ ÚÇšš ÚššÝš ŠÚš˜ õ° š¯¯ÚšŠÊ.
8MWõ¡ ŠÑš š ÚÇš ÚŠ Ë Š¯š ÚŠ¨Ú¥š š˜šˋŠ õ°ŠËš š ŠýÊš¿ŠÏÚ˜ šÊÚ¯Š Šˆ´Š¡ŠÀ š ÚÚšš¥Šˋ¯, õ°çš¿Ù šÏŠÎ 107mm, šš˜ ŠÝõ¡ R4ŠË¥ õ¯š Úš˜ ŠÏÚ˜š ššÝš DNV õñš (DNV, 2010)š šõݯښ˜ š šÚšŠÊ. 3-ŠÏÚ˜ ÚÇš Šˆ´Š¡š õ瘚ÝÚŠ õ°¥š õ°¥ šÇš š šˋŠ ÚšÊ Š¯ õý§õ° šÀ¯õÝÇš ŠÚš˜ š šÚšŠÊ. PRA õ¡¯Š¯ Š¯ DTA õ¡¯Š¯š 3-ŠÏÚ˜ ÚÇš õý¯õ°¥ŠÀš šŠ Ëš ŠÑÚ˜ŠË¥ Š¿õçÚšš¥Šˋ¯, Š õ¡¯Šý õ¯š šŠ¿Ú šŠ Ë ŠÑÚ˜š š¯´šÇõ¯ ššš Úš¡ÚšŠÊ. ŠÚ PRA Š¯ DTAš õ¡¯Š¯Ú 3-ŠÏÚ˜ ÚÇšŠýõ°¥ BV õ¯šÇŠŠ¥š¡(BV, 2014)š õý§Úšš šõݯښ˜ OPB õ¯šÝš 3õ¯šÏ š¡šËŠ Ë ššÊŠ°ŠÀ Š¿õçÚšŠÊ. 3õ¯šÏ õ¯šÝ šÑš Š¯ˋŠýš Š¯Š¥ OPB õ¯šÝš Ú¯ š¯´šÇõ¯ ššš Úš¡ÚšŠÊ. ŠÚ PRA Š¯ DTAš õ¡¯Š¯Ú 3-ŠÏÚ˜ ÚÇšŠýš õ瘚 Šˆ´Ššš š˜Š¥šÇŠˋ Šˆ´ŠŠÀš Šˆ´Š šýšÇŠË¥ õ瘊ÑÚõ¡¯ šÇŠ Êš ŠÊ. õçÙŠÑ šŠ Ëš 3õ¯šÏ Š¯ˋŠý(PRA Š¯ DTA õ¡¯Š¯š 3-ŠÏÚ˜ ÚÇšŠýõ°¥ BV õ¯šÇŠŠ¥š¡)š Š¯Š¥ Š¿õçÚ õý¯õ°¥, BV õ¯šÇŠŠ¥š¡š ŠÛš š¡šËŠ Ëšš õçÙŠÑ šŠ Ëš õ°¥š Úõ¯Úõ° Šš š¡šËŠ Ëšš õçÙŠÑ šŠ Ëš õ°¥Š Úõ¯ÚŠ õýš Úš¡ÚšŠÊ. 3-ŠÏÚ˜ ÚÇšŠýš š¡Ú¯ŠÏÚ˜ õ¯š šÎõ¯š Š¯Š¥ Š¿š Ú šŠ Ë šÏšÊ õ°šŠË¥ š šÚšš¥Š, BV õ¯šÇŠŠ¥š¡š Š¿š Ú šŠ Ë šÏšÊ õ°šŠË¥ õ° Š ÊÚ š ššŠÊ. ŠÚ Šš š¡šËŠ Ëšš õ¡õýˋÚ õçÙŠÑ šŠ Ëš õ¯šŠÀ š¡Úš˜ šŠ Ë šÏšÊ õ°šŠ ŠÏÊš¯ šššÏ š ššš 3-ŠÏÚ˜ ÚÇšŠýš¥ŠÀŠÑÚ¯ š£š š ššŠÊ.
ŠÏÚ˜š šçš õ¯šŠË¥ õý¯š Úõ¡¯ šÚ ŠÊšÊ-ŠÏÚ˜š šŠ ÇŠ ÚÇšš ÚçÚš˜ 10õ¯š ŠÏÚ˜õ¯ šçš õ¯ššš šÎŠˆ
ÚšŠÊ. ŠÚ š¡šËõ¯-š¡Ú¯ŠÏÚ˜ õ¯š õÇõ°ŠË¥ 10õ¯š ŠÏÚ˜ŠË¥ š šˋÚ ŠÊšÊ-ŠÏÚ˜ ÚÇšš ÚçÚš˜ ŠšÑÚ õý¯õ°¥ 3-ŠÏÚ˜ ÚÇššš š£š OPB õ¯šÝšÇ š¡šËõ¯-š¡Ú¯ŠÏÚ˜ õ¯š õÇõ°šŠ Š˜ÇšÚšÏ Šˆ£Ú šÚËš Š₤¡š¿ŠÊŠ š˜šÊš šÎŠˆ
ÚšŠÊ.
šõ¯ ššÙ š šýÇŠšÙÚ ÚÇšš ÚçÚš˜ š£š š¡šËŠ Ë šÇŠ Ëõ°¥ š¡šËõ¯ šÇŠ Ëš õ¯õ¯ šŠÀ š šÚššÏŠÏ, šÊš ÚšÊ š¥šÇšÊŠË¥ õ° Š ÊÚ š šýÇŠšÙÚ ÚÇšš ÚçÚ šÊšÎšÇ šõ瘊ŠÊ. ŠÚ õçÙŠÑ šŠ Ë õ°š¡ÀšÇŠ OPB Šˆ´ŠˋÚ¡ õ°š¡À šÊÚš ÚçÚš˜ 3-ŠÏÚ˜ ÚÇšŠýš š ÚŠš ŠÚš˜ õýšÎÚ Úšõ¯ šŠÊ. Š°¡ š¯õ瘚šŠ DTAõ¯ PRAš Š¿Úš˜ šÂŠ š˜šÊš õñ¥š˜Úš˜ OPB Úšš šŠÛ˜Š šÇš
Ú š šŠÊõ° šÊŠˆ
ÚššÏŠÏ, šÇš ŠÚ šÂŠ š Šš š¡ õñ¥õݯõ¯ šõ瘊ŠÊ.
Úõ¡¯
šÇ Š
¥Š˜¡š 2018Š
ÚÇššš¯ŠÑ š˜šš¥ŠÀ ÚõçÙÚÇšõ°¥Úõ¡¯š šÏÚËšš šÏšš Š¯š šÚŠ š¯õ瘚(ÚÇššŠšÏ šçŠ°çÚˋ š¡Š ËššÝ).
Fig.ô 5.
Response surface of hotspot stresses as function of OPB- and IPB-interlink angles (Choung and Lee, 2018)
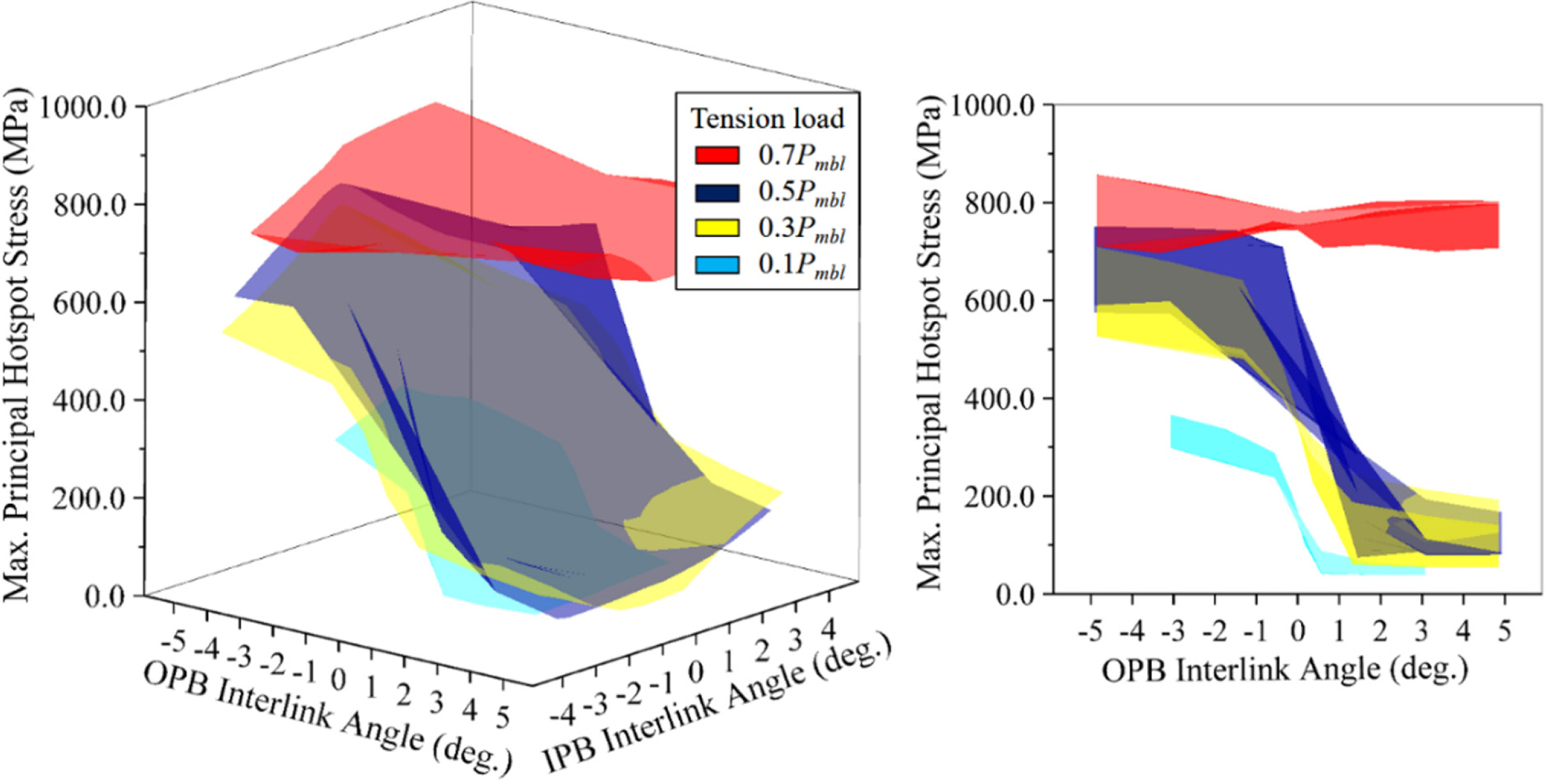
Fig.ô 6.
Flowchart for relationship of hotspot stress-interlink angle using 3-link analysis and multi-link analysis

Fig.ô 10.
Tensile and compressive stress distributions in mid-span section of the link #2 (Lee et al, 2018)

Tableô 1.
Information for nominal size D107 chain link
Tableô 2.
Summary of the number of elements.
| Element Type | Number of element |
|---|---|
| C3D8I | 60,000 |
| M3D4R | 8,000 |
| Displacement coupling | 1 |
| Sum | 68,001 |
Tableô 3.
Applied load and boundary conditions in the DTA (Choung and Lee, 2018)
References
Bureau Veritas(BV). (2014). Fatigue of Top Chain of Mooring Lines due to In-plane and Out-of-plane Bendings: Guidance Note NI 604 DT R00E. BV, France.
Choung, J., & Han, S. (2016a). A Novel Procedure for Mooring Chain Fatigue Prediction based on Maximum Principal Stress Considering Out-of-Plane and In-Plane Bending Effects. Journal of the Society of Naval Architects of Korea, 53(3), 237-248.


Choung, J., & Han, S. (2016b). A Novel Approach to Predict Mooring Chain Fatigue Considering Out-of-Plane and In-Plane Bending Effects.. Proceedings of 1st International Conference on Ships and Offshore Structures Hamburg, Germany..
Choung, J., & Lee, J. (2018). Study on Prediction of Stresses by Out-of-Plane and In-Plane Bending Moments in Offshore Mooring Chain.. Ships and Offshore Structures. 1-15.

Det Norske Veritas(DNV). (2010). Offshore Mooring Chain: Offshore Standard DNV-OS-E302., DNV, Norway.
Jean, P., Goessens, K., & LãHostis, D. (2005). Failure of Chains by Bending on Deepwater Mooring Systems.. Proceedings of the Offshore Technology Conference Houston Texas, USA..

Kim, M., & Kim, Y. (2017). Nonlinear Finite Element Analysis for Mooring Chain Considering OPB/IPB. Journal of Ocean Engineering and Technology, 31(4), 299-307.


Li, CB., Choung, J., & Noh, MH. (2018). Wide-banded Fatigue Damage Evaluation of Catenary Mooring Lines using Various Artificial Neural Networks models. Marine Structures, 60, 186-200.

Lim, Y., Kim, K., Choung, J., & Kang, C. (2010). A Study on Out-of-Plane Bending Mechanism of Mooring Chains for Floating Offshore Plants. Journal of the Society of Naval Architects of Korea, 47(4), 580-588.

Melis, C., Jean, P., & Vargas, P. (2005). Out-of-Plane Bending Testing of Chain Links.. Proceedings of 24th International Conference on Offshore Mechanics and Arctic Engineering Halkidiki, Greece..


Rampi, L., & Vargas, P. (2006). Fatigue Testing of Out-of-Plane Bending Mechanism of Chain Links.. Proceedings of 25th International Conference on Offshore Mechanics and Arctic Engineering Hamburg, Germany..


Lee, JB., Koo, W., & Choung, J. (2018). Out-of-Plane Bending Moment-Induced Hotspot Stress Evaluation Using Advanced Numerical Technique.. Proceedings of the 37th International Conference on Offshore Mechanics and Arctic Engineering Madrid, Spain..


Rampi, L., Dewi, F., & Vargas, P. (2015). Chain Out of Plane Bending(OPB) Joint Industry Project(JIP) Summary and Main Results.. Proceedings of the Offshore Technology Conference Houston Texas, USA..

Rampi, L., Dewi, F., Francois, M., Gerthoffert, A., & Vargas, P. (2016a). Chain out of Plane Bending(OPB) Fatigue Joint Industry Project(JIP) Static Test Program and OPB Interlink Stiffness.. Proceedings of the 35th International Conference on Offshore Mechanics and Arctic Engineering Busan, South Korea..


Rampi, L., Bignonnet, A., Cunff, CL., Bourgin, F., & Vargas, P. (2016b). Chain out of Plane Bending(OPB) Fatigue Joint Industry Project(JIP) Fatigue Test Program Results and Methodology.. Proceedings of the 35th International Conference on Offshore Mechanics and Arctic Engineering Busan, South Korea.


- TOOLS
-
METRICS

-
- 2 Crossref
- Scopus
- 6,553 View
- 103 Download