1. 서 론
파력발전이란 변환장치를 이용하여 파랑에너지를 인간이 사용할 수 있는 전기에너지로 변환하는 과정을 말하며, 에너지 변환과정을 크게 파랑에너지→ 기계에너지 → 전기에너지 순으로 나타낼 수 있다. 여기서 파랑에너지로부터 기계에너지로 변환하는 과정을 1차 변환이라 하며, 기계에너지에서 전기에너지로 변환하는 과정을 2차 변환이라 한다. 파랑에너지로부터 가능한한 많은 양의 전기에너지를 추출하기 위해서는 변환장치의 효율이 매우 중요하다. 많은 연구자들은 각 변환과정에서 에너지 추출효율을 높이고자 다양한 형태의 파력발전장치들을 제안하였고 관련 연구를 수행해 왔다(
Drew et al., 2009).
수직운동을 이용한 기존의 점 흡수식(Point absorber) 파력발전장치들은 대부분 원기둥 형상을 갖는 1개 또는 2개 부이(Buoy)로 구성된다. 1차 변환과정에서 에너지 추출효율을 높이기 위한 방법으로 설치지점에서 파랑에너지가 가장 밀집되어 있는 파랑스펙트럼의 최대주파수(Peak frequency)와 부이의 수직운동 고유주파수(Heave natural frequency)를 일치시키도록 설계한다(
Budar and Falnes, 1975). 이 경우, 에너지 밀도가 높은 입사파의 주파수 대역에서 공진(Resonance)이 일어나 부이의 수직운동이 크게 증가되어 1차 변환 효율을 높일 수 있다. 그러나 부이가 공진되는 주파수 대역이 좁기 때문에 공진주파수 영역에서는 부이 운동이 크게 증폭되어 에너지 흡수효율은 높아지지만 공진주파수를 벗어난 주파수 영역에서는 흡수효율이 급격히 떨어지는 단점을 가지고 있다. 따라서 실제 해상과 같이 다양한 주파수들이 섞여 있는 불규칙 파랑 중에서 가능한한 많은 에너지를 추출하려면 높은 효율을 가짐과 동시에 넓은 주파수 대역에서 에너지를 흡수할 수 있는 파력발전장치 개발이 필요하다.
이중 부이(Dual-buoy)로 구성된 파력발전장치의 대표적인 예로 Wavebob과 Power buoy 등이 있다. Wavebob은 원형 단면을 갖는 도넛형상의 흘수가 짧은 외부 부이와 원기둥 형상의 흘수가 긴 내부 부이로 구성된다. 외부 부이는 파를 따라 상하운동을 하는 반면, 내부 부이는 입사파와의 공진에 의해 크게 증폭된 수직운동을 한다. 이때 발생하는 내·외부 부이의 상대 수직운동으로부터 전기에너지를 생산한다(
Weber et al., 2009). Power buoy는 Wavebob과 비슷한 형상을 갖지만 내부 부이 바닥면에 수직운동을 저감시키는 감쇠판(Damping plate)을 부착하여 내부 부이의 수직운동을 최대한 억제하도록 설계되었다. 따라서 파를 따라 운동하는 외부 부이와 수직운동을 거의 하지않는 내부 부이 간의 상대운동을 이용하여 전기를 추출한다.
Mavrakos(2004)는 동심원상에 놓인 이중 부이의 방사문제를 고유함수전개법(Matched eigenfunction expansion method)을 이용하여 풀어 동유체력계수(부가질량, 방사감쇠계수)를 구하였다.
Chau and Yeung(2010)은
Mavrakos(2004)의 해석모델에서 외부와 내부 부이 사이의 간격이 없을 때 수직운동에 의한 동유체력을 고유함수전개법을 사용하여 구하였다.
Engstrőn et al.(2011)은 로프로 연결된 2개의 부이(원기둥+구)와 선형발전기로 구성된 파력발전장치에 대한 효율을 구하였다. 불규칙파 중에서 공진 발생 시 약 80% 파워 취득비를 얻을 수 있으며 공진발생은 설치해역의 파랑스펙트럼의 형태에 민감하게 반응함을 밝혔다. 국내에서는
Bae and Cho(2013)은 내부가 빈 원기둥 형상의 부이의 수직운동 특성을 해석하기 위하여 회절과 방사문제를 고유함수전개법을 사용하여 해석하였다. 여기서 계산된 파기진력 및 동유체력을 운동방정식에 대입하여 부이의 수직 운동특성을 살펴보고 모형실험 결과와 비교하였다.
본 논문에서는 넓은 주파수 대역에서 파랑에너지를 흡수할 수 있을 뿐만 아니라 높은 효율을 갖는 파력발전장치를 개발하기 위해 다중 공진개념을 이용하였다. 다중 공진을 발생시키기 위하여 외부와 내부 부이로 구성된 이중 부이 파력발전장치 모델을 제안하였다. 외부 부이로 내부가 빈 단순한 원기둥 형상을 갖는 기본형(Model 1)과 기본형 바깥 수면 근처에 고리 모양의 부가물을 부착한 개량형(Model 2) 모델을 사용하였다. 개량형 모델은 외부 부이의 수선면적을 늘려 외부 부이의 수직운동 고유주파수를 인위적으로 높이기 위함이다. 단순 원기둥 형태의 내부 부이는 외부 부이의 빈 공간에 위치한다. 2차 변환장치로 도입하려고 하는 선형발전기는 영구자석과 코일의 상대운동으로부터 전기를 생산하는 장치이다. 따라서 영구자석을 외부 부이에 고정하고, 코일을 내부 부이에 설치하면 내·외부 부이의 상대 수직운동이 발전효율에 중요한 요소가 된다. 본 연구에서는 선형발전기를 배제한 상태에서 파랑 중 이중 부이의 수직운동 변위를 제주대학교 2차원 수조에서 측정하였다. 모형실험은 2종류(기본형, 개량형)의 외부 부이 모델에 대하여 내부 부이의 흘수를 변경시켜가면서 각 부이의 수직운동을 측정하고 이로부터 1차 변환효율을 결정짓는 상대 수직운동을 구하였다. 이중부이 파력발전장치 중에서 개량형 외부 부이를 사용한 모델이 기본형 외부 부이 모델보다 불규칙파와 같이 넓은 주파수 대역에서 더욱 효과적으로 에너지 추출할 수 있음을 모형실험결과를 통하여 입증하였다.
2. 모형실험
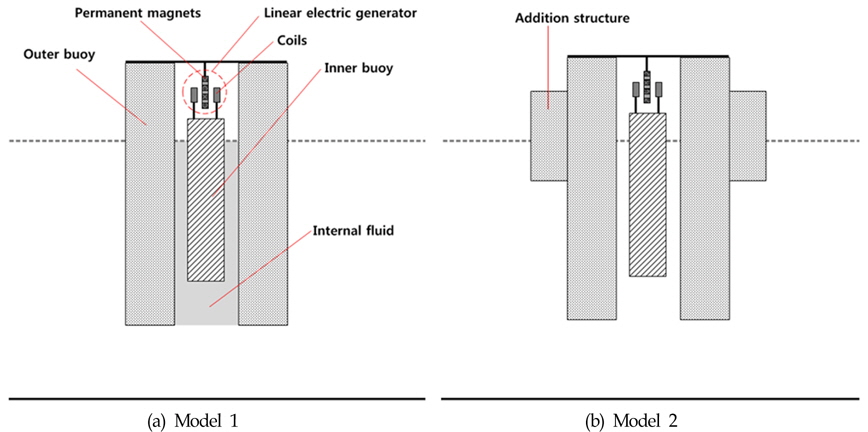
다중 공진을 발생시키기 위한 핵심은 외부 부이의 형상에 있다. 기본형(Model 1) 외부 부이는 공진을 일으키는 2개의 고유 주파수(Natural frequency)를 갖고 있다. 하나는 외부 부이 자체가 지닌 수직운동 고유주파수이며, 다른 하나는 외부 부이 안쪽 빈 공간에 채워진 내부 유체(Internal fluid)의 피스톤-모드(Piston-mode) 고유주파수이다(
Fig. 1(a) 참조). 특히 입사파 주파수와 내부 유체의 고유주파수가 일치되면, 공진에 의해 내부 유체의 상하운동이 커지게 된다. 공진으로 크게 진동하는 내부 유체를 따라 내부 부이의 수직운동도 커지게 된다. 또한 내부 부이도 외부 부이와 마찬가지로 자체의 수직운동 고유주파수를 갖고 있기 때문에 특정 주파수에서 공진에 의해 수직운동이 커질 수 있다. 따라서 내부 부이 운동에 영향을 미치는 내부 유체 공진주파수 또는 내부 부이 수직운동 공진주파수에서 내부 부이의 운동특성을 살펴보는 것이 중요하다.
Fig. 1에 제시된 이중부이 파력발전장치는 에너지 추출효율을 높이기 위하여 다중 공진을 이용하는 새로운 개념의 파력발전장치이다. 이 장치의 성능을 모형실험을 통하여 살펴보기 위하여 2차원 조파수조에 서 여러 설계 변수들을 바꿔가면서 다양한 실험을 수행하였다.
Fig. 1
Definition sketch of experimental models for a dual-buoy WEC(wave energy converter) (a: Only hallow shape, b: attached addition structure of ring shape)
2.1 실험 모델
모형실험에서는
Fig. 2와 같이 총 6개의 실험 모델을 대상으로 규칙파중 운동실험을 실시하였다.
Mij는 모형실험에서 사용한 총 6개의 실험모델을 쉽게 나타내기 위한 기호이다. 여기서
i는 외부 부이 형상을 나타내는 모델 번호를,
j는 내부 부이의 흘수를 나타내는 번호를 뜻한다. Model 1과 2는 각각 기본형과 개량형 외부 부이를 뜻한다.
j는 내부 부이의 흘수에 따라 3가지로 나타내었다. 즉, 내부 부이의 흘수가 외부 부이의 흘수보다 짧을 때는
j = 1, 같을 때는
j = 2 그리고 긴 경우는
j = 3로 구분된다. 모든 실험에서 외부 부이의 흘수는 350mm로 고정하였으며, 개량형에 부착된 고리형 부가물의 흘수는 50mm이다. 그리고 내부 부이의 흘수는 290mm(
j = 1), 350mm(
j = 2), 그리고 400mm(
j = 3)이다. 각 부이의 제원을
Table 1에 정리하였다.
Fig. 2
Six combination of experimental models for a dual-buoy WEC
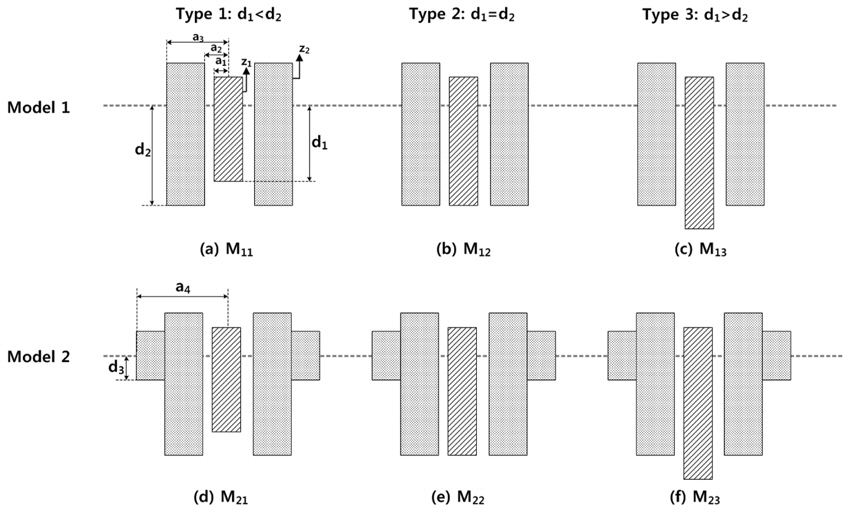
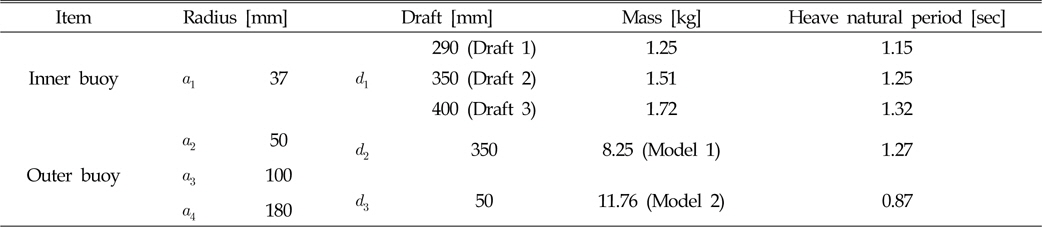
Table 1
Specification of a dual-buoy WEC
내·외부 부이의 수직운동 고유주기(
Ti)는 식 (1)과 같이 계산할 수 있으며, 내부 유체의 고유주기(
Tf)는
Fukuda(1977)가 제안한 식 (2)로부터 계산할 수 있다.
여기서
mi은 부이의 질량,
μi는 부가질량(Added mass),
ρ는 물의 밀도,
g는 중력 가속도,
Si는 수선면적을 나타낸다. 밑첨자 1은 내부 부이를, 2는 외부 부이를 뜻한다. 그리고
Sf은 내부 유체의 수선면적이다. 기본형(Model 1)과 개량형(Model 2) 외부부이의 고유주기는 각각 1.27s, 0.87s이며, 내부 유체의 고유주기는 1.25s로 기본형 외부 부이의 고유주기와 비슷한 값을 갖는다. 한편, 흘수 변화에 따른 내부 부이의 수직운동 고유주기는 각각 1.15s(
j = 1), 1.25s(
j = 2), 1.32s(
j = 3)이다.
Fig. 3은 2차원 조파주소 내에 설치된 실험 모델의 사진을 보여주고 있다.
Fig. 3
Photographs of a dual-buoy WEC in the wave tank

2.2 실험 조건
모형실험은 제주대학교 2차원 조파수조에서 실시하였다. 수조의 제원은 길이 20m, 폭 0.8m이며 수심은 0.6m이다.
Fig. 4는 모형실험의 구성도를 보여주고 있다. 수조 한쪽 끝에는 피스톤 타입의 조파기가 있으며, 반대쪽에는 경사형 소파장치가 설치되어 있다. 내·외부 부이의 수직운동 변위를 측정하기 위하여 1축 가속도계(AS-1GB)를 부이의 무게중심 위치에 설치하였다. 외부 부이에는 회전운동 변위도 함께 측정하기 위하여 2개의 가속도계를 사용하였다. 조파기로부터 약 2.8m 떨어진 위치에 용량식 파고계를 설치하여 입사파를 계측하였다. 또한 외부 부이의 무게 중심으로부터 수조 벽까지 약한 강성을 갖는 4줄의 스프링으로 연결하여 운동을 구속하지 않으면서 표류력(Drift force)으로 부이가 밀려나가는 것을 방지하였다.
Fig. 5는 조파수조
(a)와 계측 시스템
(b) 그리고 무게중심 위치에 가속도계를 설치한 내부 부이
(c)를 보여주고 있다.
Fig. 4
Schematic sketch of experimental set-up(top view)
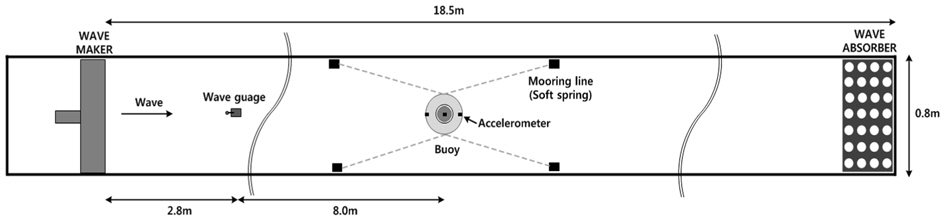
Fig. 5
Photographs of the wave tank(a), measurement systems(b) and inner buoy(c)

파랑 중 운동실험은 규칙파에 대해서 수행하였으며 내·외부 부이의 수직운동 고유주기와 내부 유체의 고유주기를 모두 포함하는 범위[0.8s 1.5s]내에 있는 총 15개의 주기에 대하여 실험을 실시하였다. 이때 파형 경사(Wave steepness: H/λ)는 0.009~0.018사이의 값을 사용하여 입사파의 파고를 정하였다.
3. 모형실험 결과 및 고찰
모형실험에서 계측한 부이의 수직운동 진폭(zai)을 입사파 진폭(A)으로 나눈 무차원화된 값(zai/A)을 운동특성을 나타내는 값으로 사용하였고, 이를 수직운동 RAO(Response amplitude operator)라 부른다. 여기서 i=1은 내부 부이, i=2는 외부 부이를 나타낸다. 실험데이터는 소파장치가 놓인 수조 끝단으로부터의 반사파가 실험모델에 도달하기 전까지의 유효한 데이터를 추출하여 분석하였고, 샘플링 주파수는 200Hz이다. 입사파의 진폭과 내·외부 부이의 수직운동 진폭 그리고 상대 운동진폭은 입사파의 파형(ζa(t))과 내부 부이 운동변위(z1(t)), 외부 부이 운동변위(z2(t)), 상대 운동변위(z2(t)–z1(t))의 시계열 자료로부터 Zero-crossing 방법을 사용하여 구한 평균값이다.
Fig. 6과
7은
Fig. 2에 나타난 기본형(Model 1)과 개량형(Model 2) 외부 부이의 수직운동 RAO를 보여주고 있다. 두 그래프 모두 측정 주기 범위 내에 1개의 피크 값을 보이며 그때의 주기는 기본형은 1.30s, 개량형은 0.85s이다. 이 값들은
Table 1에 정리한 외부 부이의 고유주기와 일치한다. 즉, 공진으로 인하여 공진주기에서 외부 부이의 수직운동 RAO는 큰 값을 갖는다. 또한 각 공진주기에서 기본형과 개량형의 수직운동 RAO의 값 차이가 나타남을 볼 수 있는데, 이는 고리모양의 부가물 부착으로 수직운동 시 점성에 의한 박리가 발생하여 감쇠효과가 증가하여 개량형의 RAO가 크게 줄어들었다. 기본형에서 외부 부이의 수직운동 RAO(
za2/
A)의 피크값은
M11 =4.3,
M12 =3.5,
M13=3.8으로 내부 부이의 흘수 변화에 따라 약간의 차이를 보이고 있다. 그러나 개량형인 경우에는 외부 부이의 피크 값은 약 2.15로 내부 부이의 흘수 변화에 관계없이 동일한 값을 준다. 이는 외부부이와 내부 부이 사이의 연성효과로 설명할 수 있다.
Fig. 8에서 살펴보듯이 기본형인 경우 주기 1.30s 부근에서 내부 부이의 수직운동 증폭비는 매우 크게 나타나서 외부 부이의 운동에 영향을 준 반면에
Fig. 9에 나타난 개량형인 경우 외부 부이의 공진주기인 0.85s에서 내부 부이의 수직운동은 거의 일어나지 않아 외부 부이의 운동에 영향을 주지 않았기 때문이다.
Fig. 6
Comparison of heave RAO of the outer buoy for Model 1 as a function of inner buoy's draft

Fig. 7
Comparison of heave RAO of the outer buoy for Model 2 as a function of inner buoy's draft
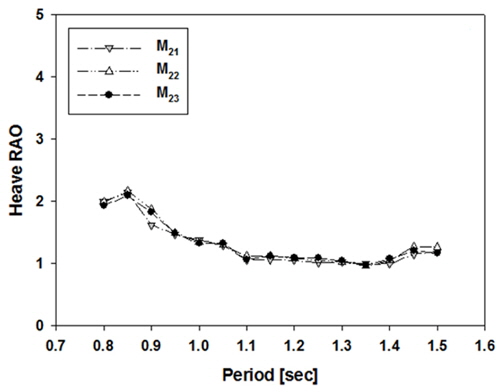
Fig. 8
Comparison of heave RAO of the inner buoy for Model 1 as a function of inner buoy's draft
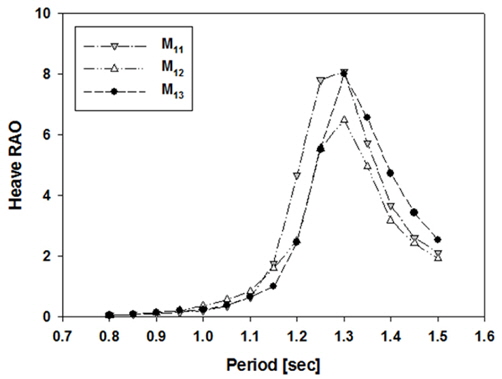
Fig. 9
Comparison of heave RAO of the inner buoy for Model 2 as a function of inner buoy's draft
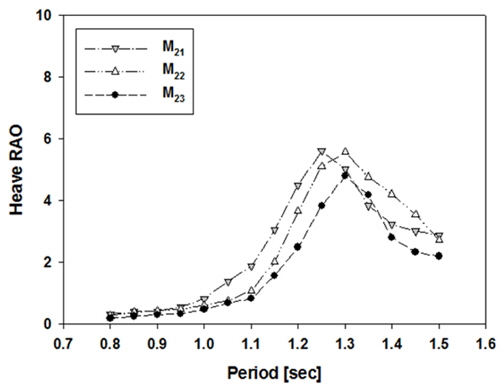
Fig. 8,
9는 기본형(Model 1)과 개량형(Model 2)에 대하여 내부 부이의 수직운동 RAO(
za1/
A) 곡선을 비교한 그림이다. 기본형과 개량형 모델 모두에서 내부 부이는 주기 1.25s와 1.30s 사이에서 운동이 크게 나타났다. 이 값들은 내부 유체의 고유주기(
Tf)와 내부 부이의 수직운동 고유주기와 일치한다. 여기서 흥미로운 사실은 내부 부이의 흘수가 외부 부이의 흘수보다 작은경우에는 내부 부이는 수직운동 고유주기에서 운동이 크게 증폭되지 않고 내부 유체 공진시 운동이 크게 일어남을 알 수 있다. 이러한 현상은 외부 부이가 내부 부이에 미치는 파를 차단하여 내부 부이에 작용하는 외력을 크게 감소시켰고, 또한 문풀(Moon pool)과 같이 닫쳐진 유체영역 내에 속한 부이의 동유체력(부가질량, 방사감쇠계수) 특성은 열린 해역에서의 부이의 운동특성과는 다른 독특한 특성을 가지고 있기 때문이다. 그러나 내부 부이의 흘수가 외부 부이 보다 긴 경우(
M13,
M23)는 외부 부이의 형태와 관계없이 내부 부이의 수직운동 고유주기(1.3s)에서 공진이 발생하였다. 내부와 외부 부이의 흘수가 같은 경우에는 내부 유체의 고유주기와 내부 부이의 수직운동 고유주기가 1.25s로 서로 같다. 실험결과에서는 고유주기 1.25s보다 약간 긴 1.3s에서 피크점이 나타났다. 2개의 고유주기가 서로 같아 실험에서의 피크값이 둘 중 어디에서 영향을 받은 것인지 명확하게 알 수는 없지만 2개의 고유주기 모두 결과에 영향을 준 것으로 예측된다.
Fig. 8과
9를 비교해 보면 공진주기에서 내부 부이의 수직운동 RAO의 피크값이 큰 차이를 보이는 것을 알 수 있다. 기본형(Model 1) 외부 부이에서는 실험모델
M11 과
M13에서 약 8배,
M12에서 6.5배의 증폭비를 나타났다. 반면에 개량형(Model 2) 외부 부이에서는 내부 부이의 RAO 피크값이 내부 부이의 흘수에 따라 약 4.8-5.6사이의 값을 보이고 있다. 이러한 결과는 앞에서 언급했듯이 기본형인 경우 주기 1.3s는 외부 부이의 공진 주기에도 해당되어 외부 부이의 큰 수직운동이 내부 부이의 수직운동에 영향을 미친 반면에 개량형인 경우에는 내부 부이의 운동이 크게 증폭되는 주기 1.3s 부근에서는 외부 부이는 파를 따라 운동하는 장주기 영역에 속하므로 그 영향이 내부 부이의 운동에 크게 나타나지 않았다.
Fig. 10(a),
(b),
(c)는 3개의 내부 부이의 흘수에 대하여 기본형과 개량형 모델의 상대 수직운동 RAO를 보여주고 있다. 비록 선형발전기를 뺀 상태에서 모형실험을 수행하였지만, 두 부이간의 상대 수직운동은 에너지 추출효율을 결정하는 가장 중요한 요소이다. 내부 부이의 흘수가 외부 부이보다 작거나 같은
Fig. 10(a),
(b)에서 개량형이 기본형에 비하여 모든 주기에서 상대 수직운동 RAO값이 더 크게 나타났다. 내부 부이의 흘수가 외부 부이보다 긴
Fig. 10(c)에서도 주기 1.25s, 1.3s를 제외한 모든 주기에서 개량형이 기본형보다 좋은 결과를 보여주고 있다. 기본형은 외부 부이의 공진주기, 내부 유체의 공진주기 그리고 내부 부이의 공진주기가 1.3s 가까이 놓여 있어 측정 주기 범위내에서 1개의 공진주기만 나타난 반면에 개량형은 외부 부이의 고유주기가 내부 부이와 내부 유체 고유주기와 멀리 떨어져 있어 2개의 공진주기가 측정 주기 범위 내에서 나타남을 보여주고 있다. 그리고 2개의 공진주기 사이의 주기범위에서도 비교적 높은 증폭비(=2)를 유지하고 있음을 볼 수 있다. 개량형 외부 부이를 갖는 파력발전장치는 넓은 주파수 대역에서 에너지를 획득할 수 있음과 동시에 다중 공진에 통해 에너지 추출효율을 증가시킬 수 있음을 잘 보여주었다.
Fig. 10
Comparison of relative heave RAO between inner and outer buoy for model 1, 2 (a: draft 1, b: draft 2, c: draft 3)

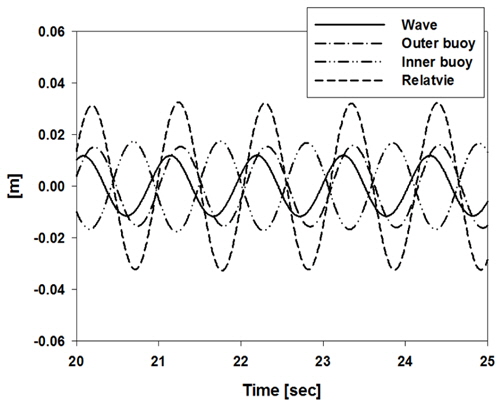
Fig. 11은 개량형 실험모델
M21에 대한 주어진 입사파 조건(주기=1.05s, 진폭=0.013m)에서의 실험결과로 입사파(실선), 외부 부이의 수직운동(일점쇄선), 내부 부이의 수직운동(이점쇄선) 그리고 내·외부 부이의 상대 수직운동(점선)을 시간에 따라 보여주고 있다. 여기서 주기 1.05s는
Fig. 10(a)에서 나타난 바와 같이 2개의 공진주기 사이에 놓인 값으로 이때 상대운동 RAO는 약 2.0이다.
Fig. 11에서 보듯이 내부와 외부 부이 각각의 수직운동 진폭은 비록 크지 않지만 두 부이간의 180도 위상차가 발생하여 상대운동이 크게 나타남을 보여주고 있다. 이러한 결과는 이중 부이 파력발전장치의 효율 측면에서 바람직하다.
Fig. 11
Time series of the model M21 in regular wave (A = 0.013 m, T = 1.05 sec)
4. 결 론
본 논문에서는 다중 공진을 이용하는 이중 부이 파력발전장치를 제안하고 파랑중 이중 부이의 수직운동 특성을 파악하고자 2차원 조파수조에서 체계적인 모형실험을 실시하였다. 시스템 안에 내재된 고유주기는 내부와 외부 부이의 수직운동 고유주기와 내부 유체의 피스톤-모드 고유주기이다. 2개의 외부 부이 모델(기본형, 개량형)에 대하여 내부 부이의 흘수(3개)를 변화시켜가면서 총 6개의 실험 모델을 제작하여 입사파의 주기를 바꿔가면서 모형실험을 실시하였다.
내부 부이의 흘수가 외부 부이 보다 짧은 경우에는 내부 부이는 내부 유체의 운동을 따른다. 따라서 내부 유체의 고유주기에서 공진으로 내부 부이는 큰 운동을 한다. 내부 부이의 흘수가 외부 부이 보다 긴 경우에는 내부 부이는 내부 유체 운동을 따르지 않고 내부 부이의 수직운동 고유주기에서 수직운동 변위가 크게 일어났다. 내부와 외부 부이의 흘수가 같을 때는 내부부이의 수직운동 고유주기와 내부 유체의 고유주기가 같기 때문에 공진의 발생 원인을 명확하게 구분하기는 어려웠다. 닫쳐진 유체영역에서 속한 내부 부이의 운동특성은 차후 파력발전장치의 형상 설계에 있어서 유용한 정보로 사용될 것으로 사료된다.
본 이중 부이 파력발전장치의 효율을 결정짓는 부이간의 상대 수직운동 RAO는 수선면적을 증가시켜 고유주기를 짧게 한개량형(Model 2)이 기본형(Model 1)보다 내부 부이의 흘수 변화에 관계없이 전 주기에 걸쳐 우수한 결과를 보였다. 특히 기본형과 달리 개량형은 측정 주기 범위 내에서 서로 다른 2개의 공진주기를 갖기 때문에 비교적 넓은 파 주파수 대역에서 에너지를 추출할 수 있는 장점을 지니고 있다. 더욱이 2개의 공진주기 사이의 주기범위 내에서도 상대 수직운동 RAO값이 떨어지지 않고 비교적 높은 증폭비(=2)를 유지하였다.
이론적으로 3개의 고유주기를 갖는 이중 부이 파력발전장치를 모형 실험한 결과 최대로 이용할 수 있는 공진주기는 개량형에서 2개였다. 이는 내부 유체 고유주기와 내부 부이 고유주기의 차가 크지 않았기 때문이다. 차후 연구에서는 내부 유체 고유주기와 내부 부이 고유주기를 일정 간격 떨어지도록 이중부이 형상을 설계하여 불규칙파와 같이 넓은 파 주파수 대역에서 더욱 더 효과적으로 에너지 추출할 수 있는 개선된 형태의 이중 부이 파력발전장치를 개발할 것이다.
감사의 글
본 연구는 2010년에 지식경제부의 재원으로 한국에너지 기술평가원(2010302007 0080)의 지원을 받아 수행한 신재생에너지기술개발사업 연구 과제입니다.
References
Bae, Y.H., Cho, I.H.. (Characteristics of Heaving Motion of Hollow Circular Cylinder, Journal of Ocean Engineering and Technology, 2013). 27(5):43-50.


Budal, K., Falnes, J.. (A Resonant Point Absorber of Ocean Wave Power, Nature, 1975). 256, 478-479 10.1038/256478a0.


Chau, F.P., Yeung, R.W.. (Inertia and Damping of Heaving Compound Cylinders The 25th International Workshop on Water Waves and Floating Bodies 2010.
Drew, B., Plummer, A.R., Sahinkaya, N.N.. (A Review of Wave Energy Converter Technology, Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2009). 233, 887-902.

Fukuda, K.. (Behavior of Water in Vertical Well with Bottom Opening of Ship and its Effects on Ship-Motion, Journal of the Society of Naval Architects of Japan, 1977). 141, 107-122.

Engstrőm, J., Kurupath, V., Lsberg, J., Leijon, M.. (A Resonant Two Body System for a Point Absorbing Wave Energy Converter with Direct-driven Linear Generator, Jouranal of Applied Physics, 2011). 110, 1-8.

Mavrakos, S.A.. (Hydrodynamic Coefficients in Heave of Two Concentric Surface-piercing Truncated Circular Cylinders, Applied Ocean Research, 2004). 26, 84-97 10.1016/j.apor.2005.03.002.

Weber, J., Mouwen, F., Parrish, A., Robertson, D..






















