1. Introduction
Fatigue study requires an advanced and combined synthetic analysis of the macro- and micro-circumstances. Because of the distinctiveness of fatigue analysis, there are many factors, including the material properties, environmental factors, and welding characteristics. There is also great uncertainty in the coefficients during the calculation or assessment process. Moreover,there are so many uncertain factors in an actual situation that fatigue analysis mainly focuses on the study of the certainty derived from a fatigue analysis method, which requires a combination of practical experiments to verify the known methods. The development of computer technology has opened up a new research direction involving rapid methods of fatigue analysis using computer simulations based on the mainstream deterministic method (Yang and Kim, 2012).
Generally, the fatigue failure process can be divided into three stages: the initiation of cracks, stable growth of cracks, and fracture (Cramer et al., 1995). There are also different reasons for fatigue failure and the destruction of the total or local intensity. The former is caused by alternating stresses, particularly the amplitudes of the alternating stresses, and the breakage is a gradual accumulation process. However, the latter is induced by an amplitude with an extreme value, which causes a sudden destruction (Mao, 2009; Fricke, 2003; Sarkani et al., 2001).
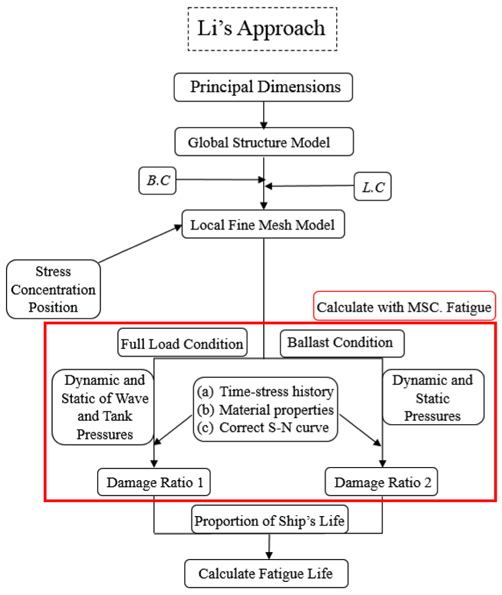
Fatigue analysis may be carried out using methods based on a fatigue test (S-N data) and the estimation of cumulative damage (Palmgren-Minner rule). In a case where the loading or geometry of the considered part is too complex, LiŌĆÖs approach (Li and Zhao, 2013) has been proposed based on MSC Fatigue. In this paper, LiŌĆÖs approach is utilized by taking a 306K crude oil tanker as an example, and the results may indicate that it is feasible to estimate the fatigue life of a ship.
2. Theory of fatigue assessment
2.1 Basic theory of LiŌĆÖs approach
Fatigue analysis may be carried out using methods based on a fatigue test (S-N data) and the estimation of cumulative damage (Palmgren-Minner rule). The long term stress range distribution is a fundamental requirement for fatigue.
The fatigue assessment of LiŌĆÖs approach is based on a finite element (FE) model, which should consider the influence of corrosion. The total corrosion addition tcorr for structural members is found as follows:

where twas is the total wastage allowance of considered structural member.
For ships, the basic loading conditions are a full load condition and ballast condition. In the theory mentioned above, in order to estimate the fatigue life of a ship, it is first necessary to calculate the alternating stresses for each loading condition. Second, the time-stress history should be obtained through a simulation of the approximate operating states in waves. Then, the damage value can be calculated using the correct S-N curve by MSC Fatigue. Finally, the fatigue life is calculated using the damage value and time-stress histories in LiŌĆÖs approach. The basic phases are shown in Fig. 1.
2.2 S-N curve and cumulative damage
Accordingto the common IACS rules (2006), the assessment of the fatigue strength of a welded structural members includes the following 3 phases:
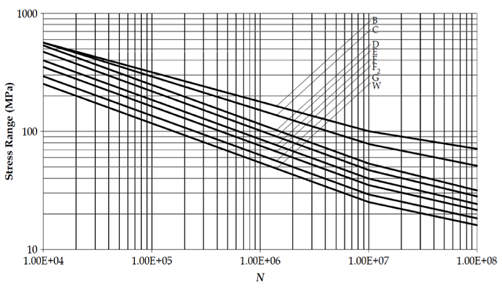
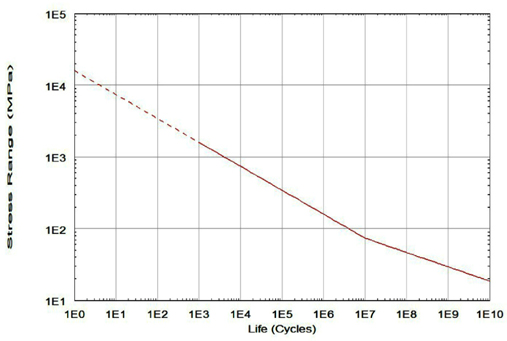
The capacity of a welded steel joints with respect to its fatigue strength is characterized by S-N curves, which give the relationship between the stress ranges applied to a given detail and the number of constant amplitude load cycles to failure (DNV, 2003). The basic designed S-N curves are shown in Fig. 2.
We assumethat the long-term distribution of stress ranges fit a two-parameter Weibull probability distribution, and the fatigue assessment of the structure is based on the application of the Palmgren-Miner cumulative damage rule (DNV, 2003).
The cumulative fatigue damage ratio, DM, should be less than one for the design life of the ship. The design life is not to be less than 25 years. The resultant cumulative damage can be found as follows:

DMi cumulative fatigue damage ratio for the applicable loading condition
The cumulative fatigue damage ratio, DM, may be converted to a calculated fatigue life using the relationshipgiven below:
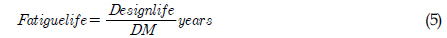
2.3 Design pressure for fatigue analysis
Generally, fatigue analyses are performed for representative loading conditions according to the shipŌĆÖs intended operation (IACS, 2006). The following two loading conditions should be examined:
The load components that should be considered are the static pressures due to loading conditions, dynamic wave pressure Pe, and dynamic tank pressure Pi. The rule expressions are adjusted for an excess probability of 10-4 per wave cycle. In general, the fatigue damage should be calculated for all representative load conditions combined with the expected operation time under each of the considered conditions.
The distribution of the dynamic wave pressures Pe is shown in Fig. 3 based on the common structural rules.
The dynamic tank pressures Pix, Piy, and Piz resulting from the longitudinal, transverse, and vertical accelerations, respectively, can be calculated. They are found as follows:



For example, Fig. 4 shows the dynamic tank pressure due to the transverse acceleration.
2.4 Calculation of pressure cycles
Because the motions of a ship are very complex during actual operations, it is difficult to predict the dynamic pressure amplitude outside the ship and thus inside the tanks (including cargo tanks and ballast tanks) using a reasonable method.
In order to approximately characterize the time-stress histories under different operating conditions of a ship, a tankŌĆÖs transverse movement cycle Ty and longitudinal movement cycle Tx can be calculated using the following formulas:


The main parameters are shown in Fig. 5.
3. TankerŌĆÖs characteristics
The principal dimensions and some of the basic data of a 306K ton crude oil tanker are presented in Table 1.
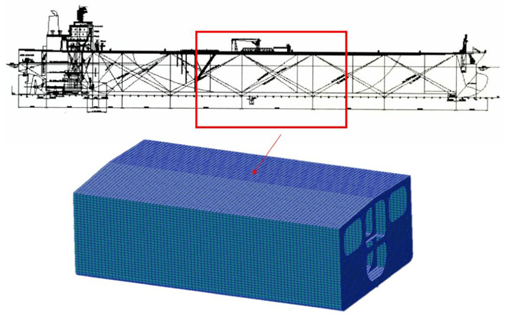
The typical mid-section of the 306K ton crude tanker is shown in Fig. 6.
The general arrangement profile and considered FE model as shown in Fig. 7. The FE model of the middle body includes 20 frames. This paperconsiders this part of the ship.
According to common structural rules, the model extent to be considered is 1/2+1+1/2 tanks.
4. Calculation and analysis
4.1 Load cases
Fatigue analyses are carried out for representative loading conditions according to the shipŌĆÖs intended operation. The following two loading conditions are examined:
The load cases are shown in Fig. 9.
4.2 Boundary condition
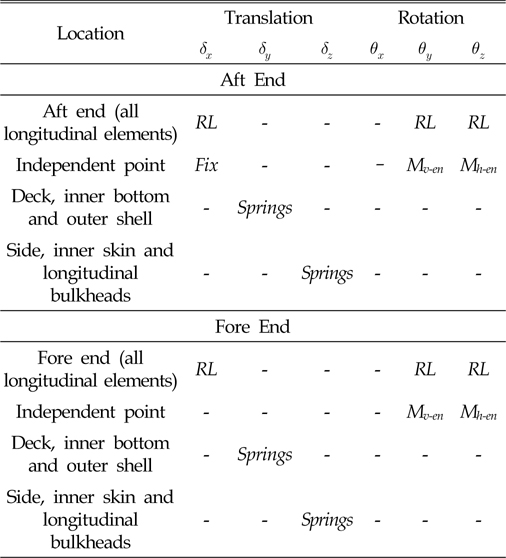
The boundary conditions used in LiŌĆÖs approach are the same as those used in a structural strength assessment. All of the boundary conditions are applied at the ends of the cargo tank FE model. These are listed in Table 2.
Ground spring elements with stiffness in global Y and Z degrees of freedom are applied on the grid points along the structures.
4.3 Stress concentration position
By adding the load cases and boundary conditions, the basic structural strength analysis can be done by MSC. Nastran. The stress concentration position would be found through this analysis.
4.4 Fatigue analysis
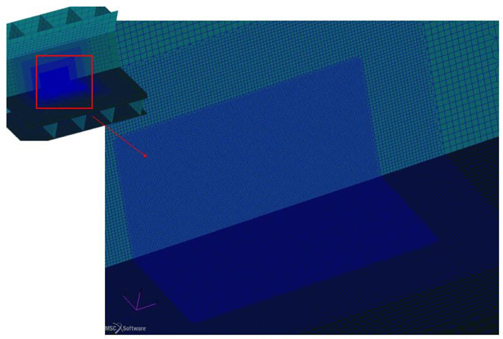
The detail model should be fine meshed in order to obtain more accurate results. This fine mesh FE model is depicted in Fig. 12, and the corrosion thickness is obtained using the fine mesh model.
The pressure described in the front may be combined in MSC Fatigue. For example, the combined static and dynamic external pressure at position Y=29m, Z=0 for the full load condition is shown in Fig. 13, and the Class D S-N curve is shown in Fig. 14.
At the same time, in order to meet the fatigue strength security requirement, the certainty of survival is taken to be 96%. The fatigue assessment results are shown in Fig. 15.
For the full load condition, the fatigue damage is found to be 2.716285├Ś10-8 according to the results, which are listed in Table 4.
The total fatigue life can be calculated as follows:
Tlife = 25/DM= 27.227 years
In order to verify the feasibility of LiŌĆÖs approach, the two methods recorded in the common structural rules were also used, namely the nominal stress method and hot spot stress method. A comparison of the results is shown in Table 5.
5. Conclusions
In the past, fatigue has been studied by various classification societies and institutions. On the basis of common structural rules, the initial fatigue strength check specification was based on an empirical formula. However, these deterministic fatigue verification methods have many disadvantages, including computational complexity and result uncertainty.
LiŌĆÖs approach using an FE method based on MSC Fatigue has been shown to be a useful method for fatigue assessment. It can be used for other concentration positions or to compare the results from other fatigue assessment methods.
In the above analysis, the basic results of a fatigue analysis of the target ship were obtained. In particular, because there are various methods for performing a fatigue assessment, it is necessary to perform a comparison between them by investigating an actual structure, and then making a comparison with simulation results in the next study.