Lamb, S.H.. (Hydrodynamics Dover Publications, 1945). p 152-155 6th Edition.
Lee, T.I., Kwon, S.H.. (A Study on Practical PMM Test Technique for Ship Maneuverability Using System Identification Method, Journal of Ocean Engineering and Technology, 16(6):2002). 25-31.
Newman, J.N.. (Marine Hydrodynamics The MIT Press, Cambridge: 1978). p 144-148.
Prestero, T.J.. (Verification of a Six-degree of Freedom Simulation Model for the REMUS AUV. Master's Thesis, Massachusetts Institute of Technology/Woods Hole Oceanographic Institution, Departments of Ocean and Mechanical Engineering; 2001.
Shin, H.K., Choi, S.H.. (Prediction of Maneuverability of KCS Using Captive Model Test, Journal of the Society of Naval Architects of Korea, 48(5):2011). 465-472 10.3744/SNAK.2011.48.5.465.


Yoon, H.K., Son, N.S.. (Estimation of Roll Related Coefficients of a Ship by Using the System Identification Method, Journal of the Society of Naval Architects of Korea, 41(4):2004). 53-58 10.3744/SNAK.2004.41.4.053.


Yun, K.H., Kim, Y.G.. (Study on the Maneuverability of Barge by Captive Model Test, Journal of Korean Navigation and Port Research, 36(8):2012). 613-618 10.5394/KINPR.2012.36.8.613.




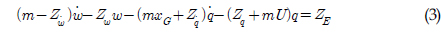
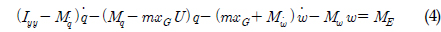
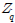 는 각가속도
는 각가속도 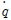 에 관한 Z력, Iyy는 y축에 관한 관성모멘트,
에 관한 Z력, Iyy는 y축에 관한 관성모멘트, 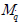 는 y축에 관한 부가 관성 모멘트, Mw는 z축 방향의 속도 w에 관한 모멘트, Mẇ는 z축 방향의 가속도 ẇ에 관한 모멘트를 나타낸다, 또한 우항에서는 외부에서의 힘 ZE′, 모멘트 ME를 각각 나타낸다(Newman, 1978).
는 y축에 관한 부가 관성 모멘트, Mw는 z축 방향의 속도 w에 관한 모멘트, Mẇ는 z축 방향의 가속도 ẇ에 관한 모멘트를 나타낸다, 또한 우항에서는 외부에서의 힘 ZE′, 모멘트 ME를 각각 나타낸다(Newman, 1978).

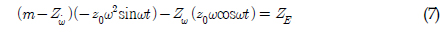
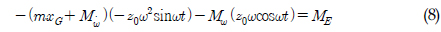


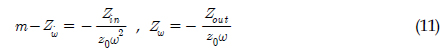
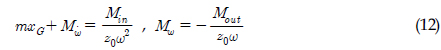

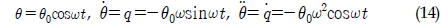
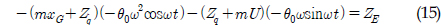
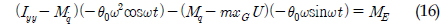


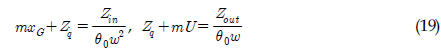

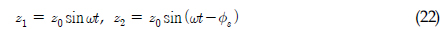
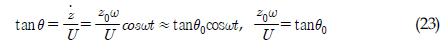

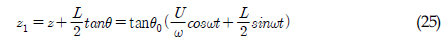
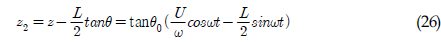
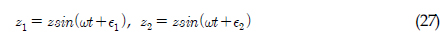

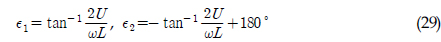
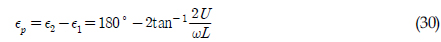

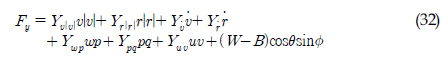
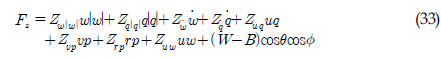
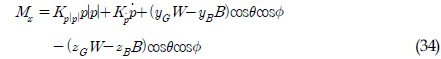
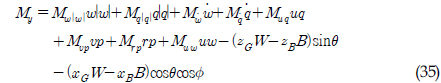

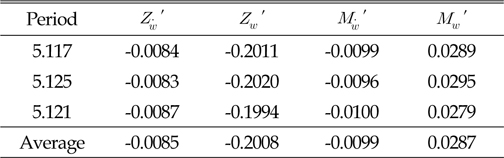
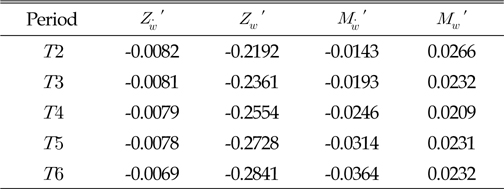
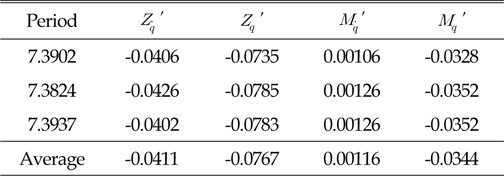
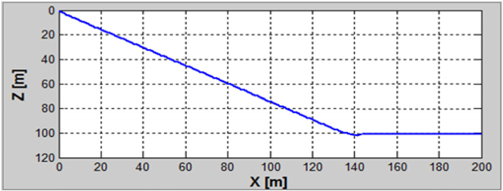
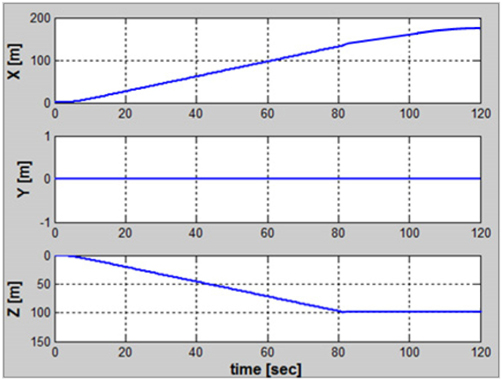
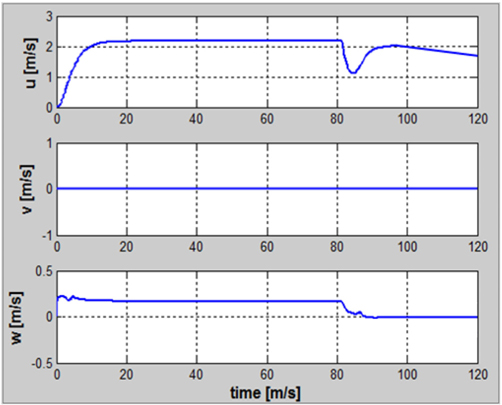
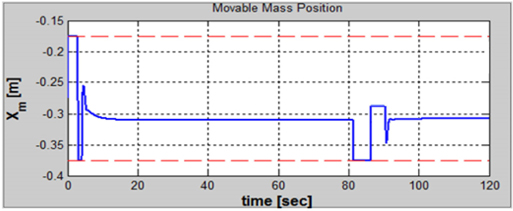
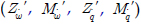 )와 REMUS AUV의 계수 추정식을 이용하여 완성된 6 자유도 운동방정식을 이용하여 시뮬레이션을 실시하였고, 설계된 심도에서의 제어가 잘 수행되는 것을 확인할 수 있었다. 한편, 부가질량력 계수의 경우, 주기가 커질수록 계수값이 감소해 짐을 보이는 반면에 Heave방향의 감쇠력 계수의 경우, 주기가 커질수록 점차 증가함을 보였다. 그리고 부가질량력이 모형 질량의 약 120%로 나타났으며 이는 수중 글라이더 모형의 긴 꼬리날개에 기인한 영향으로 판단된다. 향후 운동성능의 향상을 위해 꼬리날개의 위치, 형상, 크기 변화 등을 실시하여 그 변화와 동유체력 미계수들과의 상호 연관성 및 운동성능의 변화 등을 연구할 예정이다.
)와 REMUS AUV의 계수 추정식을 이용하여 완성된 6 자유도 운동방정식을 이용하여 시뮬레이션을 실시하였고, 설계된 심도에서의 제어가 잘 수행되는 것을 확인할 수 있었다. 한편, 부가질량력 계수의 경우, 주기가 커질수록 계수값이 감소해 짐을 보이는 반면에 Heave방향의 감쇠력 계수의 경우, 주기가 커질수록 점차 증가함을 보였다. 그리고 부가질량력이 모형 질량의 약 120%로 나타났으며 이는 수중 글라이더 모형의 긴 꼬리날개에 기인한 영향으로 판단된다. 향후 운동성능의 향상을 위해 꼬리날개의 위치, 형상, 크기 변화 등을 실시하여 그 변화와 동유체력 미계수들과의 상호 연관성 및 운동성능의 변화 등을 연구할 예정이다.