1. 서 론
세계 에너지 수요가 확대되고 얕은 바다의 석유, 가스 자원이 점차 고갈됨에 따라 글로벌 에너지 산업은 적극적으로 심해저 (Subsea) 에너지 개발에 나서고 있으며, 이로 인해 해양에너지를 탐사/시추/생산/저장하는 해양플랜트 시장이 빠르게 성장하고 있는 추세이다. 특히심해에서 다양한 목적으로 운영이 가능하고 경쟁력이 있는 부유식 해양플랜트가 주요 발주 대상이 되고 있다.
부유식 해양플랜트에 연결되어 심해저로부터 원유와 가스를 운반하는 라이져(Riser)는 지속적인 인장 변동하중과 부유식 해양플랜트의 거동으로 유기되는 다양한 동적하중을 받는다. 즉, 해풍압, 파랑, 너울등으로 인한 중주기 동하중과 부유식 해양플랜트의 작업위치를 유지하기 위해 연결된 계류라인으로 기인되는 저주기 동하중을 받는다. 이뿐 아니라 해저면으로부터 올라오는 라이져는 다양한 방향의 조류로 인해 고주기의 와류진동 (VIV, Vortex-induced vibration)을 받게되는데, 이러한 동적 복합하중은 라이져 수명에 영향을 주기 때문에 이를 고려한 설계 가 반드시 수행되어져야 한다.
따라서 라이져의 동적 복합하중은 서로 다른 동특성으로 인해 광대역 삼봉형 스펙트럼을 형성하고 피로손상에 매우 민감 하기 때문에, 라이져의 피로손상을 신뢰성있게 평가하기 위해서는 이러한 스펙트럼을 고려한 피로손상 평가방법이 체계적으로 검증될 필요가 있다.
한편, 피로연구 분야는 크게 두가지로 나눌 수 있는데, 하나는 피로실험 분야로서 실제해양구조물피로문제에 존재하는 불확실성을 극복하고자 다양한 조건하에서 시편 또는 구조물 피로실험을 수행하여 신뢰성있는 피로손상을 예측하는 분야이다. 이를 통해 S-N곡선을 제안하고 예상되는 위험수준을 고려하여 안전율을 반영한다. 나머지 피로연구 분야는 본 연구와 같이 복합적인 동적하중을 받는 구조물의 동적응답으로부터 피로손상을 예측하는 분야이다.단순 동적하중은 협대역 응답 스펙트럼을 이루고 이론적으로 레일리 분포(Rayleigh distribution)을 이루기 때문에 피로손상을 간단히 구할수 있으나(Bendat, 1964), 복합적인 동적하중은 광대역 응답 스펙트럼을 형성하고 응력범위분포를 레일리분포로 가정하는 경우 과도한 피로손상을 예측하기 때문에 합리적인 응력범위분포 및 피로손상을 예측하는 것이 이 분야의 주된 연구활동이다. 이 분야도 해당 구조물이 비선형이 강한 재료를 사용하거나 충격하중과 같이 작용하중이 비정상성을 갖는 경우에 매우 높은 불확실성이 존재한다. 하지만 일반적인 해양구조물의 응답성분은 비교적 재료의 비선형성이나 하중의 비정상성이 크게 나타나지 않기 때문에, 해양구조물 피로설계시 피로손상을 구하는데 피로손상모델 또는 협대역으로 가정하여 과도하게 피로손상 값을 예측하여 사용하고 있다(API, 2005). 아울러 해양공사 경우에 불확실성을 고려하기 위해 각 발주처의 기준에 따라 해당 위치에 안전율을 고려하고 있다.
일반적으로 광대역 동적응답을 고려할 수 있는 피로평가기법으로는시간영역피로평가법과 통계피로해석법이 대표적이다. 시간영역피로평가법은 시간영역동적응답으로부터레인플로우집계방법(Rain-flow cycle counting method)(Matsuishi and Endo, 1968)을 사용하여응력범위와그 빈도를 구하고 여기에 재료특성인 S-N(Stress-Cycle)선도와 Palmgren-Miner 선형누적법(Miner, 1945)을 적용하여 피로수명을예측하는방법이다(API, 2005). 이방법은 정도 높고직관적인 결과를 도출할 수 있는 장점이 있으나, 해당 동적응답으로부터 정상성(Stationary) 및 에르고드성(Ergodicity)을 만족하는 결과를 얻기 위해서는 충분히 긴 시간의 시간이력데이터를 확보해야 하며 정도 높은 응력범위를 얻기 위해는 충분히 짧은 샘플링 시간간격을 사용해야 하는 단점이 있다(Park et al., 2011). 이 때문에 계산비용이매우 높아 실제 설계에 적용이 어려운 실정이다. 반면, 통계피로해석법은 응답스펙트럼으로부터 피로손상모델을 사용하여 피로손상을 예측하는 방법을 말하며, 시간영역피로평가법에 비해 계산비용이 상대적으로 적은 장점이 있으나 신뢰성있는 피로수명평가를 위해서는 적용될 피로손상모델이 해당 응답스펙트럼에 적합한 모델인지가 반드시 검토되어져야 한다.
피로손상모델이란 시간영역피로평가법을 이용하여 구한 피로손상값에 상응한 결과를 얻을 수 있도록 응답스펙트럼의 모멘트와 S-N선도의 재료특성치를 인자로 하여 구성된 식을 말한다.피로손상모델은 광대역 하중으로 인한 피로손상값에 상응하는 보정계수를 제공하는 모델과 레인플로우 응력범위분포(Rain-flow stress range distribution)를 근사하는 모델로 구분된다. 보정계수를 제공하는 피로손상모델로는 광대역 응답스펙트럼을 기반으로 한 Wirsching-Light 모델(Wirsching and Light, 1980), Benasciutti-Tovo 모델(Benasciutti and Tovo, 2005) 등이 있으며, 레인플로우 응력범위분포를 근사하는 피로손상모델로는 Dirlik 모델(Dirlik, 1985), Zhao-Baker 모델(Zhao and Baker, 1992)등이 있다. 또한 최근에 Park el al.(2014)은 레인플로우 응력범위를 근사하고 광대역 및 쌍봉형 스펙트럼에 합리적인 결과를 주는 모델을 제안하였으며, 본 연구에서는 이 모델을 사용하였으며 편의상 JB모델로 정하였다. 한편, Gao and Moan(2008)은 삼봉형 스펙트럼을 대상으로 한 피로손상모델이며 Jiao-Moan 모델(Jiao and Moan, 1990)에 기초하여 개발하였으나, 이 모델을 사용하여 피로손상을 구하기 위해서는 닫힌 형태의 적분대신 적절한 수치적분을 수행해야 하는 단점이 있다. 또한 이들의 연구결과에 따르면, 이상화된 삼봉형 스펙트럼에 대하여 시간영역피로평가법으로 얻은 피로손상대비 이들의모델로부터 얻은 피로손상의 비율이 광대역 응답스펙트럼을 기반으로 한 모델들로부터 얻은 비율보다 협대역부터 광대역에 걸쳐 전반적으로 과도한 피로손상 값을 주고 이 비율에 대한 분산이 큰 결과를 주는 것을 알 수 있다. 따라서 광대역 하중을 기반으로 개발된 피로손상모델 중에서 삼봉형 스펙트럼에 적합한 모델을 찾는 것이 합리적인 접근방법이라 할 수 있다.
본연구에서는 광대역 하중을 대상으로 한 피로손상모델을 소개하고 다양한 이상화된 삼봉형 스펙트럼을 제안하며, 이들 스 펙트럼을 사용하여 광대역 하중을 기반으로 개발된 피로손상모델들로부터 얻은 피로손상값들을 합리적인 시간영역피로평가법으로부터 얻은 값들과 비교검토하고자 한다. 이로부터 삼봉형 스펙트럼에 적합한 피로손상모델을 제안하고자 한다.
2. 피로손상모델
2.1 Wirsching-Light 모델
Wirsching-Light 모델은 협대역(Narrow band) 피로손상값에 보정계수를 고려하여 광대역(Wide band) 피로손상값을 추정하는 모델이다. 이 모델은 광대역성이 비교적 약한 하중의 형태를 갖는 고정식 해양구조물의 피로해석을 대상으로 개발되었으며, 최소자승법을 사용하여 협대역 피로손상과 광대역 피로손상의 관계를 유도하였다(Wirsching and Light, 1980).
광대역 피로손상값 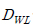 은 식 (1)과 같이 계산된다
은 식 (1)과 같이 계산된다
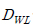 은 식 (1)과 같이 계산된다
은 식 (1)과 같이 계산된다
여기서, 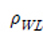 와
와  는 식 (2)와 식 (3)으로 정의되는 보정계수와 협대역 피로손상값을 각각 나타낸다.
는 식 (2)와 식 (3)으로 정의되는 보정계수와 협대역 피로손상값을 각각 나타낸다.
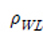 와
와  는 식 (2)와 식 (3)으로 정의되는 보정계수와 협대역 피로손상값을 각각 나타낸다.
는 식 (2)와 식 (3)으로 정의되는 보정계수와 협대역 피로손상값을 각각 나타낸다.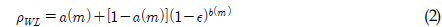
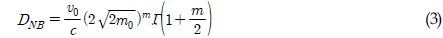
여기서, 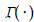 는 감마 함수이며,
는 감마 함수이며, 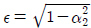 , a(m)과 b(m)은 협대역과 광대역 피로손상값에 대한 관계를 최소자승법 유도하여 식 (4)와 식 (5)와 같이 얻었다.
, a(m)과 b(m)은 협대역과 광대역 피로손상값에 대한 관계를 최소자승법 유도하여 식 (4)와 식 (5)와 같이 얻었다.
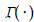 는 감마 함수이며,
는 감마 함수이며, 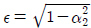 , a(m)과 b(m)은 협대역과 광대역 피로손상값에 대한 관계를 최소자승법 유도하여 식 (4)와 식 (5)와 같이 얻었다.
, a(m)과 b(m)은 협대역과 광대역 피로손상값에 대한 관계를 최소자승법 유도하여 식 (4)와 식 (5)와 같이 얻었다.

또한 m은 S-N선도의 기울기이고 C는 이 선도의 피로 재료 상수값이다. αn 는 응답스펙트럼 S (w)의 밴드폭으로 식 (6)로 정의되고, v0 와 mn는 응답스펙트럼의 영점교차주기와 n차 스펙트럼 모멘트를 각각 나타내며, 식 (7)과 식 (8)로 주어진다. 이 모델에서는 α2 를 구하기 위해 0차, 2차 그리고 4차 스펙트럼 모멘트가 사용되었다.



이 모델은 기본적으로 한 개의 기울기 m을 갖는 S-N선도의 가정하여 개발되었기 때문에, 두 개의 기울기에 대한 S-N선도 적용시 피로손상의 오차를 포함할 수 밖에 없다. 이는 수정계수 를 사용하는 모든 모델이 공통적으로 갖는 문제점이기도 하다. 또한 이 모델은 단순하고 약한 광대역 응답에 합리적인 값을 주기 때문에 상선의 피로해석에 주로 적용되고 있다.
2.2 Benasciutti‐Tovo 모델
Benasciutti-Tovo모델은 레인플로우 집계방법으로 얻은 피로 손상값(DRFC)이 식 (9)과 같이 협대역 피로손상값(DNB) 과 응력범위 계산 방법(Range counting method)으로 얻은 피로손상값 (DRC)의 사이에 존재한다는 사실로부터 유도되었다(Benasciutti and Tovo, 2005).

이를 수식화하기 위해, 가중치 bBT 를 사용하여 레인플로우 집계방법으로 얻은 피로손상값을 식 (10)와 같이 추정하였다.
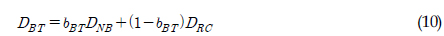
식 (10)의 DRC는 Madsen(Madsen et al., 1986)이 제안한 식을 사용하여 식 (11)과 같이 근사하였으며, 이로부터 식 (10)는 식 (12)의 광대역 피로손상 값 DBT 로 유도되었다.

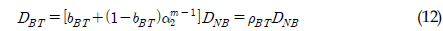
여기서, 가중치 bBT는 식 (13)로 제안하으며, α1 , α2는 해당 스펙트럼의 밴드폭으로 식(6)으로 계산된다.

2.3 Zhao‐Baker모델
Zhao‐Baker모델은 레인플로우 응력범위분포가 한개의 와이블확률분포(Weibull PDF(probability density funciton))와 한개의 레일리확률분포(Rayleigh PDF)의 조합으로 이루어져 있다고 식 (14)와 같이 가정하였다(Zhao and Baker, 1992).
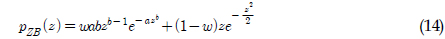
여기서, α = 8 - 7α2 , 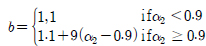 이고, 가중치 w는 식 (15)과 같다. 또한 z는 표준화된 독립변수로
이고, 가중치 w는 식 (15)과 같다. 또한 z는 표준화된 독립변수로 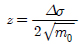 이고, α2는 해당 스펙트럼의 밴드폭으로 식(6)으로 계산된다.
이고, α2는 해당 스펙트럼의 밴드폭으로 식(6)으로 계산된다.
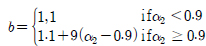 이고, 가중치 w는 식 (15)과 같다. 또한 z는 표준화된 독립변수로
이고, 가중치 w는 식 (15)과 같다. 또한 z는 표준화된 독립변수로 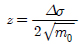 이고, α2는 해당 스펙트럼의 밴드폭으로 식(6)으로 계산된다.
이고, α2는 해당 스펙트럼의 밴드폭으로 식(6)으로 계산된다.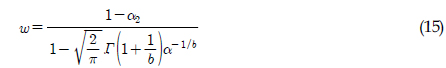
이로부터 유도된 피로손상값은 식 (16)과 같다
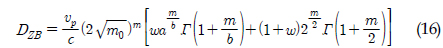
여기서, 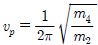 는 피크교차주기이고, m은 S-N선도의 기울기이고 C는 이 선도의 피로 재료 상수값이다.
는 피크교차주기이고, m은 S-N선도의 기울기이고 C는 이 선도의 피로 재료 상수값이다.
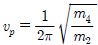 는 피크교차주기이고, m은 S-N선도의 기울기이고 C는 이 선도의 피로 재료 상수값이다.
는 피크교차주기이고, m은 S-N선도의 기울기이고 C는 이 선도의 피로 재료 상수값이다.2.4 Dirlik 모델
Dirlik모델은 레인플로우 응력범위분포가 한개의 지수확률분포(Exponential PDF)과 두개의 레일리확률분포의 조합으로 이루어져 있다고 식 (17)과 같이 가정하였으며, 이로부터 피로손상값을 예측하는 모델이다(Dirlik, 1985). 이는 협대역과 광대역 스펙트럼에 대해 안정적인 피로손상값을 주는 것으로 알려져 있다.
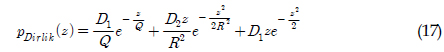
여기서, z는 표준화된 독립변수이고,

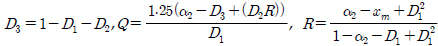
이 식에서 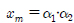 이며
이며 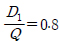 임을 알 수 있고, α1 , α2는 해당 스펙트럼의 밴드폭으로 식(6)으로 계산된다.
임을 알 수 있고, α1 , α2는 해당 스펙트럼의 밴드폭으로 식(6)으로 계산된다.
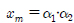 이며
이며 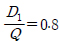 임을 알 수 있고, α1 , α2는 해당 스펙트럼의 밴드폭으로 식(6)으로 계산된다.
임을 알 수 있고, α1 , α2는 해당 스펙트럼의 밴드폭으로 식(6)으로 계산된다.식 (17)로부터 피로손상은 식 (18)과 같이 구해진다.
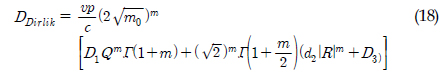
여기서, vp 는 피크교차주기이고, m은 S-N선도의 기울기이고 C는 이 선도의 피로 재료 상수값이다.
2.5 JB모델
JB 모델은레인플로우 응력범위분포를 한개의 반쪽 가우시안 확률분포(Half Gaussian PDF)와 두개의 레일리확률분포(Rayleigh PDF)를 사용하여 식 (19)과 같이 근사한 모델이다(Park et al, 2014). 이 모델도 협대역 및 광대역 스펙트럼에 대해 안정적인 피로손상값을 주는 것으로 평가되었다.
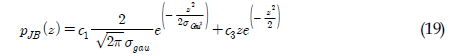
여기서, z는 표준화된 독립변수이다. 이로부터 유도된 피로손상모델은 식 (20)과 같다.

여기서, vp 는 피크교차주기이고, m은 S-N선도의 기울기이고 C는 이 선도의 피로 재료 상수값이다.
위 식의 변수들은 식 (21)에서 식 (30)으로 정의되는데, 계수 c2, c3 그리고 σGau이 음수가 되는 경우를 배제하기 위해 두 가지의 형태로 제안하였다.
c2가 양수가 될 조건CMRRR(2) > CMRR(3), c3가 양수가 될 조건 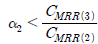 그리고 σGau가 양수가 될 조건
그리고 σGau가 양수가 될 조건 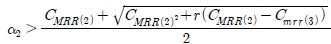 또는
또는  인 경우에 식 (20) 의 계수들은 식 (21)에서 식 (25)로 적용된다.
인 경우에 식 (20) 의 계수들은 식 (21)에서 식 (25)로 적용된다.
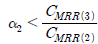 그리고 σGau가 양수가 될 조건
그리고 σGau가 양수가 될 조건 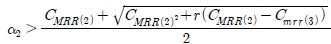 또는
또는  인 경우에 식 (20) 의 계수들은 식 (21)에서 식 (25)로 적용된다.
인 경우에 식 (20) 의 계수들은 식 (21)에서 식 (25)로 적용된다.

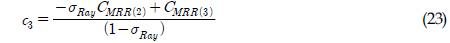


그 외의 경우에는 식 (26)에서 식 (30)으로 적용된다.





여기서, 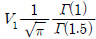 이다. CMRR(1) = α2, CMRR(2) = α0.95α1.97, CMRR(3) = α0.54 α0.93 α1.95 이며, 이 αn 값들은 해당 스펙트럼의 밴 드폭으로 식(6)으로 계산된다. 이 계수들 CMRR(1) , CMRR(2) , CMRR(3)은 Dirlik(1985)이 제안한 MRR(Moments of Rainflow stress Range distribution)을 사용하여 구한 값이며, 이 MRR은 레인플로우 응력범위의 확률분포에 대한 모멘트와 제안된 응력범위 확률분포의 모멘트의 비로 정의된다. Park el al.(2014)은 다양한 광대역 스펙트럼을시간영역으로 확장하여 레인플로우 응력범위의 확률분포를 구하였고, 식 (19)와의 비를 계산하여 1차, 2차 그리고 3차의 모멘트에 대한 MRR값들을 계산하였다. 이로부터 CMRR(1) , CMRR(2) , CMRR(3)은 계산된 MRR값들과 스펙트럼 밴드폭의 조합의 최소자승법을 사용하여유도되어졌다.
이다. CMRR(1) = α2, CMRR(2) = α0.95α1.97, CMRR(3) = α0.54 α0.93 α1.95 이며, 이 αn 값들은 해당 스펙트럼의 밴 드폭으로 식(6)으로 계산된다. 이 계수들 CMRR(1) , CMRR(2) , CMRR(3)은 Dirlik(1985)이 제안한 MRR(Moments of Rainflow stress Range distribution)을 사용하여 구한 값이며, 이 MRR은 레인플로우 응력범위의 확률분포에 대한 모멘트와 제안된 응력범위 확률분포의 모멘트의 비로 정의된다. Park el al.(2014)은 다양한 광대역 스펙트럼을시간영역으로 확장하여 레인플로우 응력범위의 확률분포를 구하였고, 식 (19)와의 비를 계산하여 1차, 2차 그리고 3차의 모멘트에 대한 MRR값들을 계산하였다. 이로부터 CMRR(1) , CMRR(2) , CMRR(3)은 계산된 MRR값들과 스펙트럼 밴드폭의 조합의 최소자승법을 사용하여유도되어졌다.
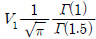 이다. CMRR(1) = α2, CMRR(2) = α0.95α1.97, CMRR(3) = α0.54 α0.93 α1.95 이며, 이 αn 값들은 해당 스펙트럼의 밴 드폭으로 식(6)으로 계산된다. 이 계수들 CMRR(1) , CMRR(2) , CMRR(3)은 Dirlik(1985)이 제안한 MRR(Moments of Rainflow stress Range distribution)을 사용하여 구한 값이며, 이 MRR은 레인플로우 응력범위의 확률분포에 대한 모멘트와 제안된 응력범위 확률분포의 모멘트의 비로 정의된다. Park el al.(2014)은 다양한 광대역 스펙트럼을시간영역으로 확장하여 레인플로우 응력범위의 확률분포를 구하였고, 식 (19)와의 비를 계산하여 1차, 2차 그리고 3차의 모멘트에 대한 MRR값들을 계산하였다. 이로부터 CMRR(1) , CMRR(2) , CMRR(3)은 계산된 MRR값들과 스펙트럼 밴드폭의 조합의 최소자승법을 사용하여유도되어졌다.
이다. CMRR(1) = α2, CMRR(2) = α0.95α1.97, CMRR(3) = α0.54 α0.93 α1.95 이며, 이 αn 값들은 해당 스펙트럼의 밴 드폭으로 식(6)으로 계산된다. 이 계수들 CMRR(1) , CMRR(2) , CMRR(3)은 Dirlik(1985)이 제안한 MRR(Moments of Rainflow stress Range distribution)을 사용하여 구한 값이며, 이 MRR은 레인플로우 응력범위의 확률분포에 대한 모멘트와 제안된 응력범위 확률분포의 모멘트의 비로 정의된다. Park el al.(2014)은 다양한 광대역 스펙트럼을시간영역으로 확장하여 레인플로우 응력범위의 확률분포를 구하였고, 식 (19)와의 비를 계산하여 1차, 2차 그리고 3차의 모멘트에 대한 MRR값들을 계산하였다. 이로부터 CMRR(1) , CMRR(2) , CMRR(3)은 계산된 MRR값들과 스펙트럼 밴드폭의 조합의 최소자승법을 사용하여유도되어졌다.3. 수치해석 및 고찰
3.1 이상화된 삼봉형 스펙트럼
본 수치해석에 사용한 스펙트럼의 개략적인 모습은 Fig. 1(a)와 같이 이상화(Idealized)된 스펙트럼 S(w)이며, 각각의 스펙트럼 피크는 협대역을 갖는다. 또한 스펙트럼 Fig. 1(a)의 시간이력 X(t)은 Fig. 1(b)와 같다. 실제 라이져의 응답은 각 스펙트럼피크가대역폭(Bandwidth)을 갖는 광대역이어서Fig. 1과 같은 스펙트럼이 이를 포함하지 못할 수 있으나,사용된 피로손상모델들이 광대역 스펙트럼을 기반으로 개발되었기 때문에 본 연구의 결과로부터 삼봉형 광대역 스펙트럼을 받는 라이져 피로손상에 적합한 피로손상모델을 제안할 수 있을 것으로 사료된다.
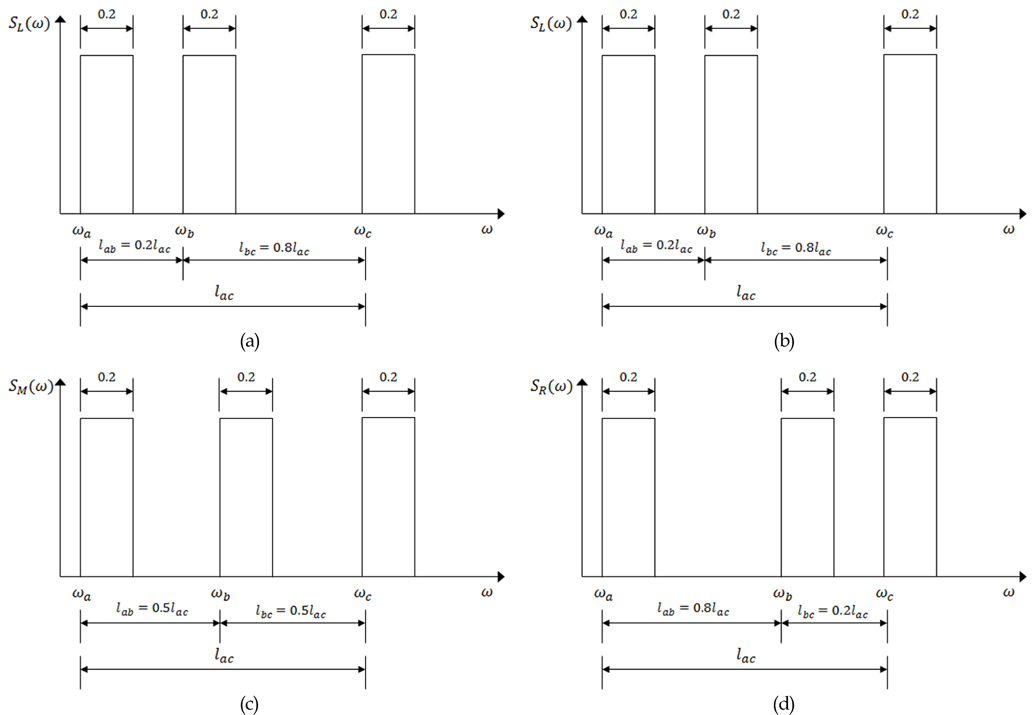
스펙트럼의 면적을 무차원화 하기 위해 세로축의 단위는 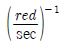 를 사용하였으며, 이상화된 삼봉형 스펙트럼의 총 면적은 1000으로 하였으며, 각 스펙트럼의 폭은 협대역 스펙트럼을 구성하기 위해 0.2rad/sec로 하였다. 본연구에사용한이상화된스펙트럼의 저주기 및 고주기스펙트럼피크의위치를현실적으로 구현하려 하였다. 즉,저주기 스펙트럼의 시작점 wa는충분히 낮은 영역의 주파수인 0.05rad/sec로 정하였고, 고주기 스펙트럼의 시작점 wc는 4.5rad/sec로 정하였다. 이 고주기 스펙트럼은 Chen and Kim (2010)이 수행한 와류진동 실험이 0.2Hz에서 2.0Hz 범위에서 이루어진 것을 참고하여 이들 범위내에 있는 값을 사용한 것이다. 이 고주기 스펙트럼은 더 높은 주파수로 정할 수 있으나, 이러한 경우에 해당 스펙트럼이 더 높은 광대역성을 보이는 것 외에 사용된 피로손상모델들의 적용에는 문제가 없고 본 연구에서 제안한 삼봉형 스펙트럼이 본 연구의 결과를 참고하여 보면 충분한 광대역성을 갖는 것을 알 수 있기 때문에, 제안한 스펙트럼만을 사용하여도 삼봉형 스펙트럼에 적합한 피로손상 모델을 제안할 수 있으리라 사료된다.반면, 시간영역피로평가법을 수행할 때에는 해당 스펙트럼의 무작위 시계열이 더 빨리 변화하기 때문에, 해당 시계열의 피크값 및피로해석에 사용될 응력범위를 얻기 위해 좀 더 조밀한 시간간격으로 수치해석을 수행해야 한다. 즉, 고주기 스펙트럼의 주파수가 2배 높아지면 시간영역피로평가법에 사용되는 시간간격은 2배로 조밀해야 한다. 또한중주기 스펙트럼 피크의 위치는 다양한 주파수의 파랑하중을 이상화하기 위해 저주기 스펙트럼과 고주기 스펙트럼사이에 Fig. 2와 같이 크게 3가지로 위치시켰다. 즉, Fig. 2(a)와 같이 중주기 주파수가 저주파 스펙트럼과 고주파 스펙트럼거리의 20%에 위치하는 경우로 이를 SL(w)로 정의하였고, Fig. 2(b)와 같이 이들 중간에 놓인 경우로이를 SM(w)로 정의하였으며, 그리고 Fig. 2(c)와 같이중주기 주파수가 저주파 스펙트럼과 고주파 스펙트럼거리의 80%에 위치하는 경우로 이를 SR(w)로 정의하였다.
를 사용하였으며, 이상화된 삼봉형 스펙트럼의 총 면적은 1000으로 하였으며, 각 스펙트럼의 폭은 협대역 스펙트럼을 구성하기 위해 0.2rad/sec로 하였다. 본연구에사용한이상화된스펙트럼의 저주기 및 고주기스펙트럼피크의위치를현실적으로 구현하려 하였다. 즉,저주기 스펙트럼의 시작점 wa는충분히 낮은 영역의 주파수인 0.05rad/sec로 정하였고, 고주기 스펙트럼의 시작점 wc는 4.5rad/sec로 정하였다. 이 고주기 스펙트럼은 Chen and Kim (2010)이 수행한 와류진동 실험이 0.2Hz에서 2.0Hz 범위에서 이루어진 것을 참고하여 이들 범위내에 있는 값을 사용한 것이다. 이 고주기 스펙트럼은 더 높은 주파수로 정할 수 있으나, 이러한 경우에 해당 스펙트럼이 더 높은 광대역성을 보이는 것 외에 사용된 피로손상모델들의 적용에는 문제가 없고 본 연구에서 제안한 삼봉형 스펙트럼이 본 연구의 결과를 참고하여 보면 충분한 광대역성을 갖는 것을 알 수 있기 때문에, 제안한 스펙트럼만을 사용하여도 삼봉형 스펙트럼에 적합한 피로손상 모델을 제안할 수 있으리라 사료된다.반면, 시간영역피로평가법을 수행할 때에는 해당 스펙트럼의 무작위 시계열이 더 빨리 변화하기 때문에, 해당 시계열의 피크값 및피로해석에 사용될 응력범위를 얻기 위해 좀 더 조밀한 시간간격으로 수치해석을 수행해야 한다. 즉, 고주기 스펙트럼의 주파수가 2배 높아지면 시간영역피로평가법에 사용되는 시간간격은 2배로 조밀해야 한다. 또한중주기 스펙트럼 피크의 위치는 다양한 주파수의 파랑하중을 이상화하기 위해 저주기 스펙트럼과 고주기 스펙트럼사이에 Fig. 2와 같이 크게 3가지로 위치시켰다. 즉, Fig. 2(a)와 같이 중주기 주파수가 저주파 스펙트럼과 고주파 스펙트럼거리의 20%에 위치하는 경우로 이를 SL(w)로 정의하였고, Fig. 2(b)와 같이 이들 중간에 놓인 경우로이를 SM(w)로 정의하였으며, 그리고 Fig. 2(c)와 같이중주기 주파수가 저주파 스펙트럼과 고주파 스펙트럼거리의 80%에 위치하는 경우로 이를 SR(w)로 정의하였다.
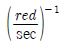 를 사용하였으며, 이상화된 삼봉형 스펙트럼의 총 면적은 1000으로 하였으며, 각 스펙트럼의 폭은 협대역 스펙트럼을 구성하기 위해 0.2rad/sec로 하였다. 본연구에사용한이상화된스펙트럼의 저주기 및 고주기스펙트럼피크의위치를현실적으로 구현하려 하였다. 즉,저주기 스펙트럼의 시작점 wa는충분히 낮은 영역의 주파수인 0.05rad/sec로 정하였고, 고주기 스펙트럼의 시작점 wc는 4.5rad/sec로 정하였다. 이 고주기 스펙트럼은 Chen and Kim (2010)이 수행한 와류진동 실험이 0.2Hz에서 2.0Hz 범위에서 이루어진 것을 참고하여 이들 범위내에 있는 값을 사용한 것이다. 이 고주기 스펙트럼은 더 높은 주파수로 정할 수 있으나, 이러한 경우에 해당 스펙트럼이 더 높은 광대역성을 보이는 것 외에 사용된 피로손상모델들의 적용에는 문제가 없고 본 연구에서 제안한 삼봉형 스펙트럼이 본 연구의 결과를 참고하여 보면 충분한 광대역성을 갖는 것을 알 수 있기 때문에, 제안한 스펙트럼만을 사용하여도 삼봉형 스펙트럼에 적합한 피로손상 모델을 제안할 수 있으리라 사료된다.반면, 시간영역피로평가법을 수행할 때에는 해당 스펙트럼의 무작위 시계열이 더 빨리 변화하기 때문에, 해당 시계열의 피크값 및피로해석에 사용될 응력범위를 얻기 위해 좀 더 조밀한 시간간격으로 수치해석을 수행해야 한다. 즉, 고주기 스펙트럼의 주파수가 2배 높아지면 시간영역피로평가법에 사용되는 시간간격은 2배로 조밀해야 한다. 또한중주기 스펙트럼 피크의 위치는 다양한 주파수의 파랑하중을 이상화하기 위해 저주기 스펙트럼과 고주기 스펙트럼사이에 Fig. 2와 같이 크게 3가지로 위치시켰다. 즉, Fig. 2(a)와 같이 중주기 주파수가 저주파 스펙트럼과 고주파 스펙트럼거리의 20%에 위치하는 경우로 이를 SL(w)로 정의하였고, Fig. 2(b)와 같이 이들 중간에 놓인 경우로이를 SM(w)로 정의하였으며, 그리고 Fig. 2(c)와 같이중주기 주파수가 저주파 스펙트럼과 고주파 스펙트럼거리의 80%에 위치하는 경우로 이를 SR(w)로 정의하였다.
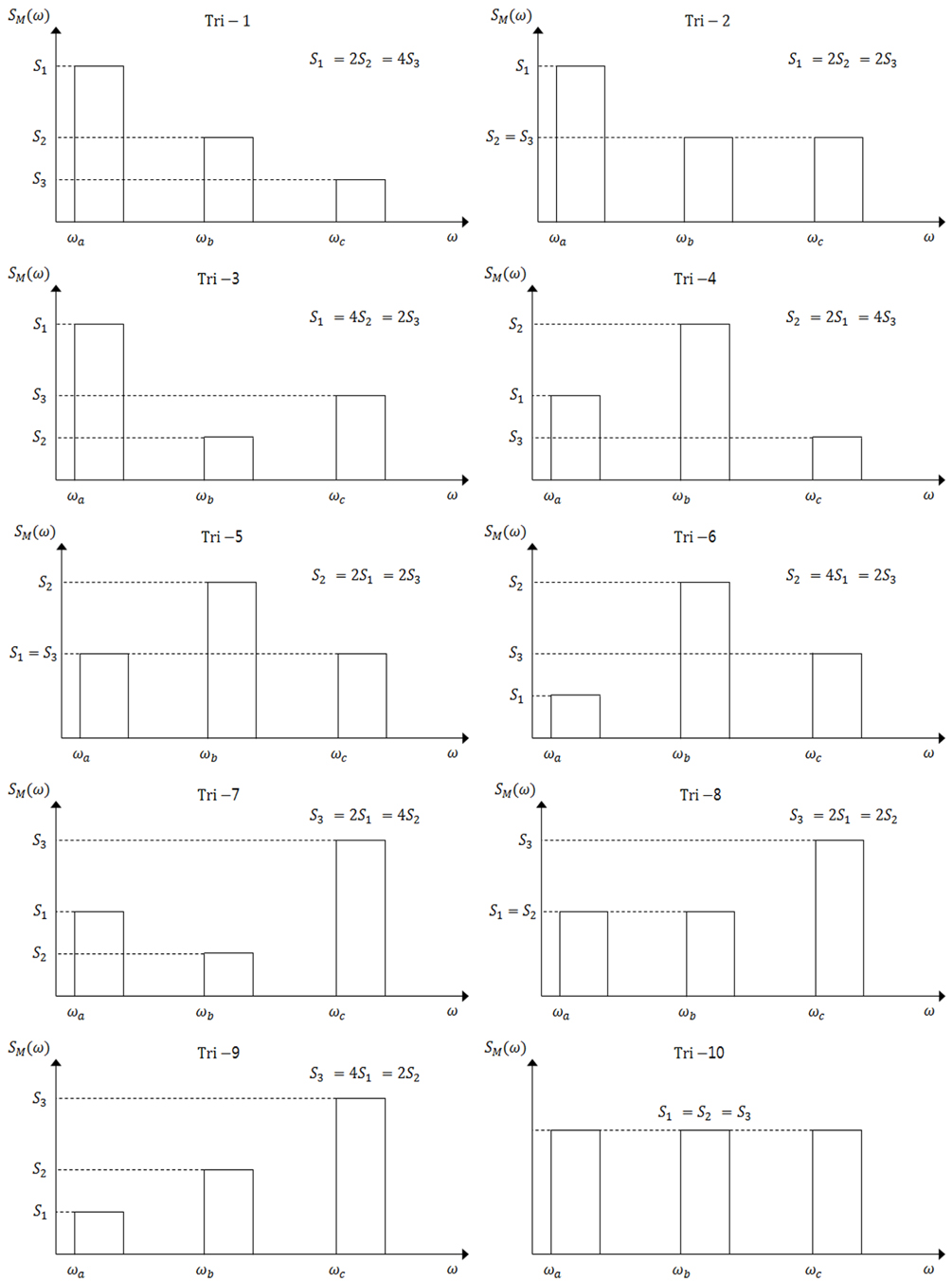
를 사용하였으며, 이상화된 삼봉형 스펙트럼의 총 면적은 1000으로 하였으며, 각 스펙트럼의 폭은 협대역 스펙트럼을 구성하기 위해 0.2rad/sec로 하였다. 본연구에사용한이상화된스펙트럼의 저주기 및 고주기스펙트럼피크의위치를현실적으로 구현하려 하였다. 즉,저주기 스펙트럼의 시작점 wa는충분히 낮은 영역의 주파수인 0.05rad/sec로 정하였고, 고주기 스펙트럼의 시작점 wc는 4.5rad/sec로 정하였다. 이 고주기 스펙트럼은 Chen and Kim (2010)이 수행한 와류진동 실험이 0.2Hz에서 2.0Hz 범위에서 이루어진 것을 참고하여 이들 범위내에 있는 값을 사용한 것이다. 이 고주기 스펙트럼은 더 높은 주파수로 정할 수 있으나, 이러한 경우에 해당 스펙트럼이 더 높은 광대역성을 보이는 것 외에 사용된 피로손상모델들의 적용에는 문제가 없고 본 연구에서 제안한 삼봉형 스펙트럼이 본 연구의 결과를 참고하여 보면 충분한 광대역성을 갖는 것을 알 수 있기 때문에, 제안한 스펙트럼만을 사용하여도 삼봉형 스펙트럼에 적합한 피로손상 모델을 제안할 수 있으리라 사료된다.반면, 시간영역피로평가법을 수행할 때에는 해당 스펙트럼의 무작위 시계열이 더 빨리 변화하기 때문에, 해당 시계열의 피크값 및피로해석에 사용될 응력범위를 얻기 위해 좀 더 조밀한 시간간격으로 수치해석을 수행해야 한다. 즉, 고주기 스펙트럼의 주파수가 2배 높아지면 시간영역피로평가법에 사용되는 시간간격은 2배로 조밀해야 한다. 또한중주기 스펙트럼 피크의 위치는 다양한 주파수의 파랑하중을 이상화하기 위해 저주기 스펙트럼과 고주기 스펙트럼사이에 Fig. 2와 같이 크게 3가지로 위치시켰다. 즉, Fig. 2(a)와 같이 중주기 주파수가 저주파 스펙트럼과 고주파 스펙트럼거리의 20%에 위치하는 경우로 이를 SL(w)로 정의하였고, Fig. 2(b)와 같이 이들 중간에 놓인 경우로이를 SM(w)로 정의하였으며, 그리고 Fig. 2(c)와 같이중주기 주파수가 저주파 스펙트럼과 고주파 스펙트럼거리의 80%에 위치하는 경우로 이를 SR(w)로 정의하였다.저주기, 중주기, 고주기 스펙트럼의 에너지 비율은 Fig. 3과 같이 10개의 형태로 이상화하였다. 따라서, Fig.2와 Fig.3으로부터 이상화된 삼봉형 스펙트럼의 다양한 조합을 생성하였으며, 총 30개의 이상화된 삼봉형 스펙트럼을 생성하였다. 이는 응답 스펙트럼이 해당 라이져의 사양 및 강성과 해상상태에 따라 매우 다양하게 생성되기 때문에, 가능한 다양한 형태의 삼봉형 스펙트럼이 발생하도록 형상화한 것이다.이 이상화된 삼봉형 스 펙트럼을 사용하여 시간영역피로평가법 수치해석을 수행하였고,삼봉형 응답스펙트럼을 보이는 라이져 구조물의 피로해석에 적합한 피로손상모델을 찾고자 하였다.
3.2 삼봉형 스펙트럼의 시간영역피로평가법
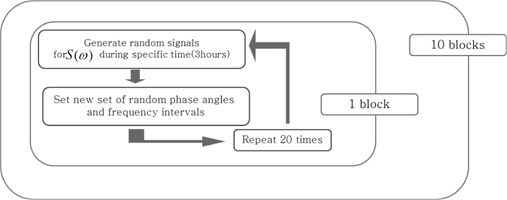
시간영역피로평가법은 시간영역 시계열의 정상 에르고드성 및 신뢰성있는 응력범위를 얻어야 하며, 이를 위해 Park이 제안한 방법을 사용하였고 이를 Fig.4과 같이 도표로 나타내었다 (Park et al., 2011). Fig. 4에서 보이는 바와 같이 한 블록당 60 시간을 전개하였으며, 총 10블록을 사용하여 600시간의 시계열값을 얻었다. 한 개의 블록은 60시간의 무작위 시계열이 얻어지는데, 이로부터 레인플로우 집계방법을 사용하여 각 블록당의 응력범위분포를 구하였다. 최종 응력확률분포는 10개의 블록으로부터 얻은 응력범위분포를 평균하고 표준화된 독립변수 z로 재구성하였다. 여기서 사용한 레인플로우 집계방법은 ASTM(1985)에서 제안한 3-points 알고리즘을 사용하였다.
또한 역푸리에 변환에 신뢰성있는 응력범위를 얻기 위해, 0.1초의 시간간격을 사용하였고 20,000개의 무작위간격 주파수와 각 해당되는 주파수에 무작위 위상차를 생성하였다. 이로부터 얻은 피로손상의 결과를 해당되는 삼봉형 스펙트럼의 기준 피로손상값으로 정의하였다.
3.3 피로손상모델 비교 분석
앞서 제안한 30개의 삼봉형 스펙트럼을 사용하여 각각의 피로 손상모델들을 비교하였다. Fig. 5(a)는 S-N선도의 기울기가 m =3인 경우이고 Fig. 5(b)는 m =5인 경우로 구분하여 도시하였으며, 이 결과는 각각의 피로손상모델을 적용한 피로손상값 D (models)과 시간영역피로평가법을 사용하여 얻은 피로손상값 D (RFD)의 비로 산출하였다. 즉, 제안된 각 스펙트럼을 3.2절에 제안한 방법으로 시간영역피로 평가법을 수행하였으며, 이로부터 얻어진 피로손상 결과를 기준으로 사용된 피로손상모델들로 예측된 결과의 비를 구하였다. Fig.5에서 보는 바와 같이D (models) / D (RFD)값이 1이면 피로손상모델이 예측한 값이 시간영역피로평가법으로부터 얻은 결과와 같다는 것을 의미한다. Fig. 5의 결과들이 피로손상값들의 비를 나타내기 때문에, S-N선도의 피로 재료 상수값 C는 서로 상쇄되어 결과값에는 영향을 주지 않으며, 계산한 결과값들은 Vanmarcke (1972) 밴드폭 매개변수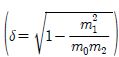 에 대해 정리하였다. 이 Vanmarcke 밴드폭 매개변수는 스펙트럼의 협대역과 광대역정도를 나타내는데 일반적으로 사용되는 변수이며,이 값이 1에 가까울수록 스펙트럼이 광대역임을 의미하고 0에 가까우면 협대역임을 의미한다. 그러므로 본 연구에 사용된 삼봉형 스펙트럼각각은 협대역 스펙트럼이나 이들 스펙트럼이 합쳐지면서 상당한 광대역 특성을 보이는 것을 알 수 있으며, Fig. 5에서 알 수 있듯이 D (models) / D (RFD)가 1에 가까운 값은 주는 피로손상모델일수록 신뢰도가 높은 모델임을 알 수 있다.
에 대해 정리하였다. 이 Vanmarcke 밴드폭 매개변수는 스펙트럼의 협대역과 광대역정도를 나타내는데 일반적으로 사용되는 변수이며,이 값이 1에 가까울수록 스펙트럼이 광대역임을 의미하고 0에 가까우면 협대역임을 의미한다. 그러므로 본 연구에 사용된 삼봉형 스펙트럼각각은 협대역 스펙트럼이나 이들 스펙트럼이 합쳐지면서 상당한 광대역 특성을 보이는 것을 알 수 있으며, Fig. 5에서 알 수 있듯이 D (models) / D (RFD)가 1에 가까운 값은 주는 피로손상모델일수록 신뢰도가 높은 모델임을 알 수 있다.
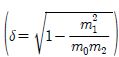 에 대해 정리하였다. 이 Vanmarcke 밴드폭 매개변수는 스펙트럼의 협대역과 광대역정도를 나타내는데 일반적으로 사용되는 변수이며,이 값이 1에 가까울수록 스펙트럼이 광대역임을 의미하고 0에 가까우면 협대역임을 의미한다. 그러므로 본 연구에 사용된 삼봉형 스펙트럼각각은 협대역 스펙트럼이나 이들 스펙트럼이 합쳐지면서 상당한 광대역 특성을 보이는 것을 알 수 있으며, Fig. 5에서 알 수 있듯이 D (models) / D (RFD)가 1에 가까운 값은 주는 피로손상모델일수록 신뢰도가 높은 모델임을 알 수 있다.
에 대해 정리하였다. 이 Vanmarcke 밴드폭 매개변수는 스펙트럼의 협대역과 광대역정도를 나타내는데 일반적으로 사용되는 변수이며,이 값이 1에 가까울수록 스펙트럼이 광대역임을 의미하고 0에 가까우면 협대역임을 의미한다. 그러므로 본 연구에 사용된 삼봉형 스펙트럼각각은 협대역 스펙트럼이나 이들 스펙트럼이 합쳐지면서 상당한 광대역 특성을 보이는 것을 알 수 있으며, Fig. 5에서 알 수 있듯이 D (models) / D (RFD)가 1에 가까운 값은 주는 피로손상모델일수록 신뢰도가 높은 모델임을 알 수 있다.Fig. 5
Results of fatigue damage of tri‐modal spectrum by fatigue damage models for (a)m = 3, (b) m = 5.
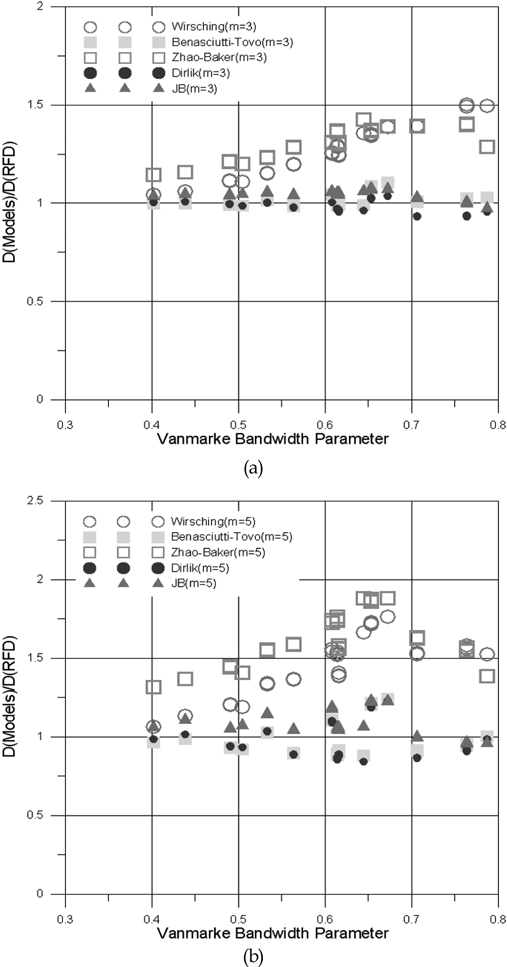
본 연구로 얻어진 결과로부터 Wirsching-Light 모델과 Zhao- Baker모델은 Vanmarke 밴드폭 매개변수가 1에 가까와지고 광대역으로 갈수록 피로손상값이 과대평가되는 경향을 보이는 것을 알 수 있며, 반면 Dirlik모델은 전반적으로 안정적이나 전반적으로 다소 과소평가되는 것을 알 수 있다. 한편, Benasciutti- Tovo 모델과 JB모델이 전반적으로 광대역 하중에서도 안정적이며 시간영역 피로평가법의 결과와 매우 유사한 피로손상값을 주는 것을 알 수 있다.
해양 플랜트를 설계하는 경우와 마찬가지로 라이져의 설계에도 매우 높은 안전율을 요구하기 때문에, 과대평가를 하는 피로 손상모델을 사용하여 설계를 하는 것이 현실적인 방법일 수 있다. 하지만 실제 문제의 경우, 수많은 복합적인 환경하중에 대 해서 과대평가를 하는 피로손상모델을 사용하여 막연히 충분한 안전율이 고려되었을 것이라 판단하고 설계하기 보다는 합리적으로 평가하는 피로손상모델을 사용하여 얻은 피로손상값을 얻은 후에 정량적인 안전율을 고려하여 설계하는 것이 더 바람직한 접근방법이 될 것으로 사료된다.
따라서, 본 연구결과로부터 삼봉형 스펙트럼의 동적하중을 받는피로손상평가에는 Benasciutti-Tovo 모델과 JB모델이 가장 적합한 모델임을 알 수 있다.
4. 결 론
본 연구에서는 광대역 응답스펙트럼의 피로손상해석에 적용되는 다양한 피로손상모델들을 소개하였고, 라이져 피로해석에 적합한 피로손상모델 선정을 위한 수치해석적 비교연구를 수행하였다. 수치해석 대상모델로는 다양한 형태의 삼봉형 스펙트럼을 정의하였으며, 이를 사용하여 레인플로우집계방법에 근거한 시간영역피로평가법을 사용하여 기준값이 되는 피로손상값을 구하였다. 또한 각각의 피로손상모델들을 적용하여 피로손상값을 구하고 이를 기준 피로손상값과 비교하여 각 모델의 적합성을 평가하였다. 그 결과 라이져와 같은 삼봉형 스펙트럼을 받는 구조물의 피로해석에는 Benasciutti-Tovo모델과 JB모델이 안정적이고 적합한 모델임을 확인할 수 있었다. 본 연구의 결과는 라이져피로강도 해석에 유용하게 사용될 수 있으리라 기대되며, 본 연구를 바탕으로 추후에 이상화된 삼봉형 스펙트럼의 정식화하는 연구를 수행할 계획이다.