1. 서 론
최근 해양공학 분야에서 다양한 목적으로 비강재 재료의 사용이 증가하고 있다. 해양구조물의 주구조물에 복합재료인 콘크리트의 적용이나 극한해양환경에 놓이는 해양플랜트 구조물에 적용되는 방한재료, 계류선에 적용되는 와이어 로프 등 다양한 부위에 강재가 아닌 재료들의 사용이 늘어나는 추세에 있다. 해양플랜트의 생애주기(Life cycle)는 20년으로 설계되는 것이 일반적이며 특정해역에 설치/운영되어 고장 및 사고 시, 유지보수가 용이하지 않으므로 구조적 안전성 및 신뢰성 확보를 위한 노력들이 다수 이루어지고 있다. 특히 최근 수명연장(25년~30년)을 위하여 구조적 안전성이 더욱 중시되고 있는 상황이다.
해양플랜트 구조물이나 선박에서 충격 완화나 진동억제 등 탄성이 필요한 부위에는 대변형 상태에서도 탄성을 유지하며 응력-변형률이 비선형 관계를 보이는 초탄성 재료(Hyperelastic material)가 주로 사용된다. 탄성체의 주요성능 평가를 위한 중요인자 중 하나는 반력을 얼마나 확보할 수 있느냐 하는 것이며, 실제 초탄성 재료를 적용하고자 하는 부위에 적절한 강성을 확보하고 반력성능을 보장하는 설계를 위해서는 ASTM(American Society for Testing and Materials)이나 ISO(International Organization for Standardization) 등 국제규격에 따른 구조재료의 실험을 통한 재료특성을 파악하여 해석을 통해 예측하는 것이 매우 중요하다. 특히, 초탄성 재료는 기본원료 및 첨가물에 따라 다양한 특성을 갖기 때문에 규격화된 물성이 존재하지 않으므로 신뢰도 높은 실험과 대상재료의 거동특성을 모사할 수 있는 적절한 비선형 재료모델을 선택하는 것이 매우 중요하다.
초탄성 재료에 대한 실험과 해석에 대한 국외 연구는 50년대에 Rivlin, 70년대에 Ogden 등이 변형률 에너지 함수를 기반으로 비선형 대변형 재료모델을 제시하였으며 90년대에는 Arruda와 Boyce 등이 8-체인(Eight-chain) 분자구조를 이용한 재료모델을 제안하는 등 재료모델에 대한 지속적인 연구가 수행되고 있다. 또한 초탄성 재료의 실험과 관련하여 시편의 형상에 따른 영향(Wada et al., 2002)에 대한 연구가 진행되었다.
반면, 국내에서는 한국기계연구원에서 수행된 “기계시스템 원천기술개발 - 초탄성체 고무류 기계부품의 변형해석 및 설계 기술 개발(KIMM, 1999)”을 통하여 초탄성 재료의 실험 및 해석과 관련하여 기존의 연구를 정리하였으며 초탄성 재료의 운용환경(온도, 노화등)에 대한 연구도 수행되었으나 실험에 의한 물성 평가에 한정되어 수행되었다(Woo and Park, 2007). 다만, 국내의 초탄성 재료의 실험 및 해석 관련 연구는 주로 고무 제품의 설계를 위한 과정으로서 수행되고 있으며 수치 해석 분야 및 해석 기술과 설계기술과의 연계 등 비선형 재료모델의 정확도에 대한 연구는 많이 부족한 실정이다.
본 연구에서는 미국재료시험협회 규격(ASTM), 국제표준화기구 규격(ISO), 한국공업규격(KS, Korean Industrial Standards)을 상세히 조사 및 분석하고 ISO규격에 따라 인장 및 압축실험을 수행하였다. 또한 대표적인 5종의 비선형 재료모델을 적용하여 유한요소 해석을 수행하고 실험결과와의 비교를 통하여 대상 시편 특성에 부합되는 재료모델을 선정하고자 하였다.
2. 초탄성 재료의 특성 실험
2.1 실험 규격 및 절차
초탄성 재료 (탄성중합체) 실험 관련 규격은 Table 1과 같으며 각각의 규격은 탄성체의 종류, 실험 종류에 따라 세부적으로 분리되어 있으므로 실험 신뢰성을 높이기 위해서는 대상재료 및 실험에 따라 규격을 선택해야 한다. 단, KS규격은 KS-ISO규격으로 통합되어 ISO규격과 동일하다.
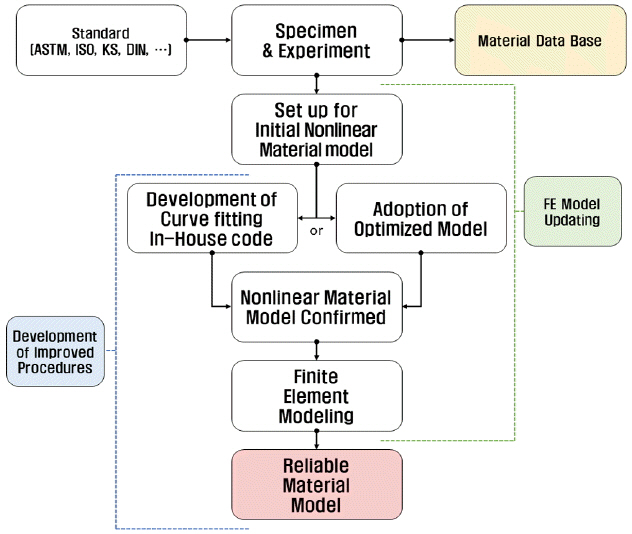
Fig. 1은 신뢰성이 높은 재료모델을 선택하기 위하여 본 연구에서 적용된 일련의 과정을 보여주고 있다. 우선, 정해진 규격에 따라 인장 및 압축 시편을 제작하고 실험을 수행하여 하중-변위 및 응력-변형률 선도를 확보한다. 다음단계에서 확보된 선도를 기반으로 곡선 적합(Curve-fitting)을 통하여 비선형 재료모델의 재료상수값을 도출하고 모델 업데이트 등이 적용된 유한요소해석을 수행하여 실험결과와 비교를 통하여 최적의 모델을 선정하였다. 본 연구에서는 유한요소모델의 생성과 비선형 재료모델을 적용한 구조해석은 상용 유한요소해석 프로그램인 Abaqus를 사용하였다.
2.2 인장 및 압축실험
일반적으로 고무재료는 기본재료와 첨가물에 따라 다양한 특성을 가질 수 있으며 본 연구에서는 천연고무에 황을 첨가한 신장률이 약 400%인 재료를 대상으로 실험을 수행하였으며 실제 사용된 인장 및 압축 실험 시편은 Fig. 2와 같다.
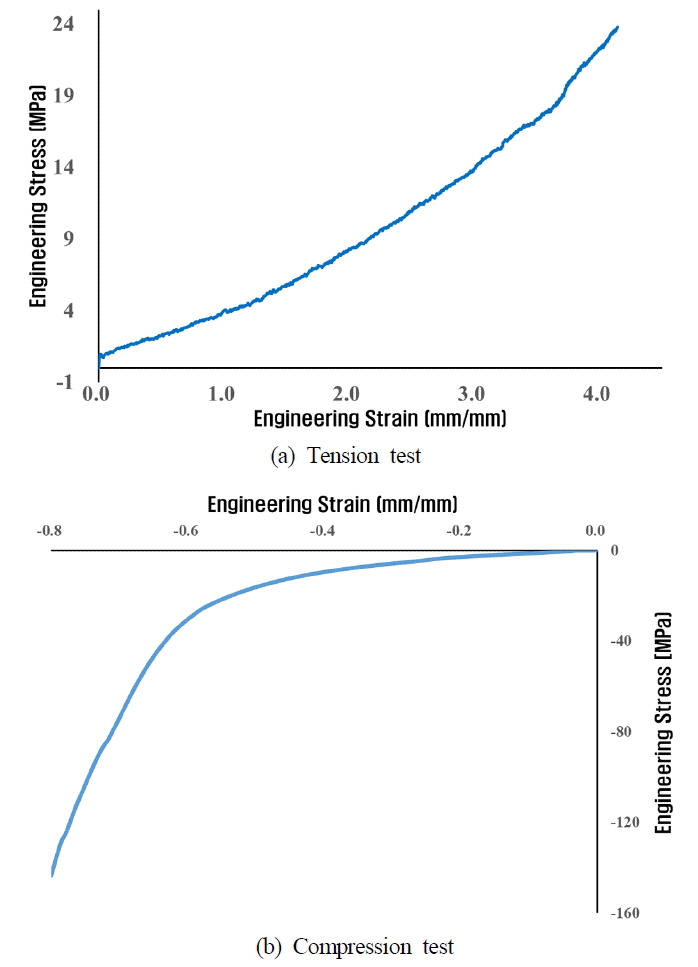
Fig. 3은 Instron 5982 장비와 영상 신율계(Video extensometer)를 사용하여 변형률을 측정하고 있는 인장 및 압축실험을 보여주고 있다.
2.3 데이터의 보정
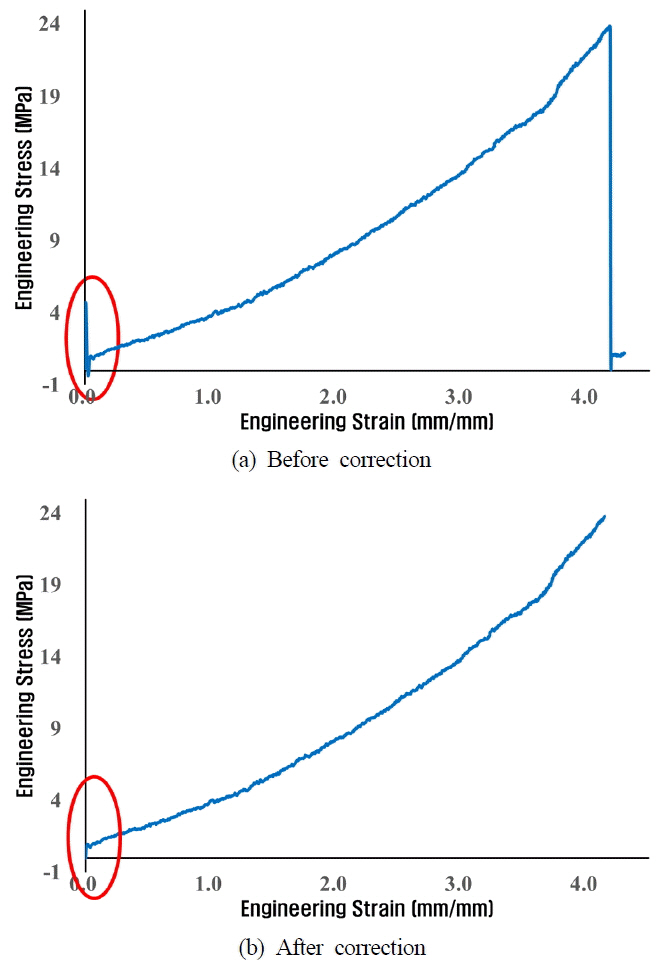
인장 실험의 경우, 실험장비 특성상 500mm/min의 빠른 속도로 수행되어 실험 초기 구간에서 Peak point가 발생하므로 비선형 재료 상수의 정확도 및 신뢰성 향상을 위하여 실험데이터의 보정이 필요하다. Fig. 4(a)는 인장 실험 데이터의 원시 데이터(Raw data)로 수평축은 변형률(Strain), 수직축은 응력(Stress)이다.
Fig. 4(a)와 같이 인장실험의 경우, 빠른 실험 구동 속도로 인하여 초기 하중-변형률 구간에서 외란(Disturbance)에 의한 오버슈트(Overshoot) 현상이 발생 할 수 있다. 이는 실제 하중 및 변형률 측정이 불안정하게 기록 될 수 있으므로 데이터를 보정하는 과정이 필요하다. 만약 오버슈트 구간을 단순히 삭제할 경우에는 보정이 되지 않거나 또는 오차 발생 가능성이 커지므로 초기 데이터 상태에 따른 보정 여부 판단을 하여 수행하여야 한다. 초기 하중의 오버슈트 구간은 전체 변형률에 있어 1% 미만으로 매우 짧으므로 단순 영점 보정으로 초기 오버슈트 구간을 제거하고 제거된 구간만큼을 오프셋 하는 절차로 진행하였으며 보정된 결과는 Fig. 4(b)와 같다.
일반적으로 초탄성 재료는 초기 가해진 하중보다 더 큰 하중을 받을 경우 응력 연화(Softening)가 발생하며 이를 Mullins 효과라 한다. 압축실험의 경우, Mullins 효과에 의하여 동일한 변형률에서도 응력이 낮게 측정될 수 있으므로 반복 실험(부하-재하)을 통한 물성 안정화 과정이 필요하다(Kim et al., 2004). 따라서 본 연구에서는 반복 실험을 통하여 시편의 안정화 과정을 거친 후 실험을 수행하였으며 실험데이터는 식 (1)을 적용하여 보정을 수행하였다.
여기서, σ는 단면적 변화를 고려한 응력, F는 실험 시 기록된 최대하중, A'o는 실험 전 시편의 공칭 단면적, Ao는 안정화 과정에서 발생한 변형을 고려한 단면적, l'o는 실험 전 표점거리, εp는 소성 거동에 의한 소성변형률, σ'는 실험에 의한 공칭응력이다.
3. 탄성체의 기하학적 비선형 해석
3.1 비선형 재료모델
초탄성 재료의 거동 모사를 위한 다양한 비선형 재료모델이 존재하며 본 연구에서는 일반적으로 가장 많이 사용되는 5종의 비선형 재료모델을 대상으로 하였으며 관련 이론식은 다음과 같다.
(1) Neo-Hookean model
Neo-Hookean 모델은 탄성고체에 대한 후크의 법칙을 대변형에 적용할 수 있도록 확장한 것이며, 1948년 Rivlin에 의해 제안되었다. 변형에너지는 제 1 불변량으로 표현되어 다음과 같다.
여기서, C1는 실험데이터의 곡선 적합을 통하여 결정되는 모델상수이며 I1은 주변형률 불변량(Principal strain invariant)이다.
(2) Mooney-Rivlin model
Mooney-Rivlin 모델은 Neo-Hookean 모델에서 제 2 불변량을 포함하는 것으로 다음 식과 같이 확장할 수 있다. 본 연구에서는 2차식을 적용하였다(Rivlin and Saunders, 1951).
여기서, C10과 C01는 실험데이터의 곡선 적합을 통하여 결정되는 모델 상수이며 Ii는 주변형률 불변량이다.
(3) Ogden model
Ogden 모델은 변형에너지를 변형률의 다항식으로 표현된다. 본 연구에서는 3차식을 적용하였다(Ogden et al., 2004).
여기서, αp와 μp는 실험데이터의 곡선 적합을 통하여 결정되는 모델 상수이며 λi는 주연신율(Principal stretch ratio)이다.
3.2 해석모델의 구성
구조해석과 전후처리는 상용 유한요소해석 프로그램인 Abaqus를 사용하였다. 초탄성 재료의 유한요소모델링을 위한 요소의 특성을 검토한 결과 솔리드, 트러스, 빔, 쉘 요소의 적용이 가능하나 대변형률(Large strain) 구현이 가능한 하이브리드 요소를 사용하는 것이 적절한 것으로 판단된다. 이는 고무와 같은 초탄성 재료는 대변형이 발생하기 때문에 유한요소모델의 구성 시, 일반적으로 구조해석에서 사용되는 소변형률 요소의 사용은 정확성을 크게 낮출 수 있으므로 비압축성 거동 구현이 가능한 복합솔리드 요소(6-node linear triangular prism, Hybrid, Constant pressure, C3D6H와 8-node linear brick, Hybrid, Constant pressure, Hourglass control, C3D8RH)를 적용하였다. Fig. 6은 초탄성 재료의 인장 및 압축실험을 모사하기 위한 각각의 유한요소모델을 보여주고 있다. 유한요소모델의 요소망 크기를 조밀하게 적용하면 해석결과의 정확도는 올라가지만 증가하는 절점과 요소에 대한 자유도가 증가하여 해석시간이 크게 증가할 수 있다.
다만, 변형이 발생하지 않는 지그로 고정되는 그립부와 변형이 크게 발생하는 중앙부의 요소 크기의 변화를 크게 두면 세 장비로 인한 오차가 발생하여 해의 수렴성을 저해할 수 있으므로 요소의 밀도를 높이고 형상의 건전성을 확보하고자 하였다. 인장실험의 경우, 중앙부위의 변형이 가장 크기 때문에 조밀한 요소를 적용하였으며 지그에 고정된 그립부등 변형이 작은 구간은 요소밀도를 낮추어 구성하였다. 실제 구현된 인장실험에 대한 유한요소모델의 요소 크기는 그립구간은 1.50mm, R1 part는 0.65mm, R2 part는 1.20mm, GL part는 0.35mm이며 압축모델의 경우는 전체적으로 압축변형에 관한 거동이 잘 표현될 수 있도록 0.65mm로 모델을 구성하였다.
특히, 인장실험 모사를 위한 유한요소해석 모델은 경계조건이 비대칭으로 주어지므로 전체 유한요소모델(Full FE model)을 사용하는 것이 적절하다. 다만 요소의 대칭성에 대한 검토를 위하여 대칭모델(Symmetric FE model)에 대한 비교를 수행하였다. Fig. 7는 전체 유한요소 모델과 대칭모델을 보여주고 있다. Table 4는 Neo-Hookean 모델을 적용하여 해석한 결과로 특정변형지점에서의 변위가 전체 유한요소모델과 대칭모델이 동일함을 확인하였으며 인장실험 모사를 위한 유한요소해석은 전체 유한요소모델을 사용하였다.
3.4 경계조건
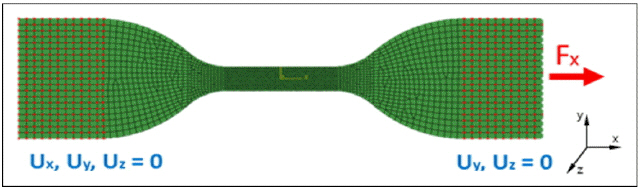
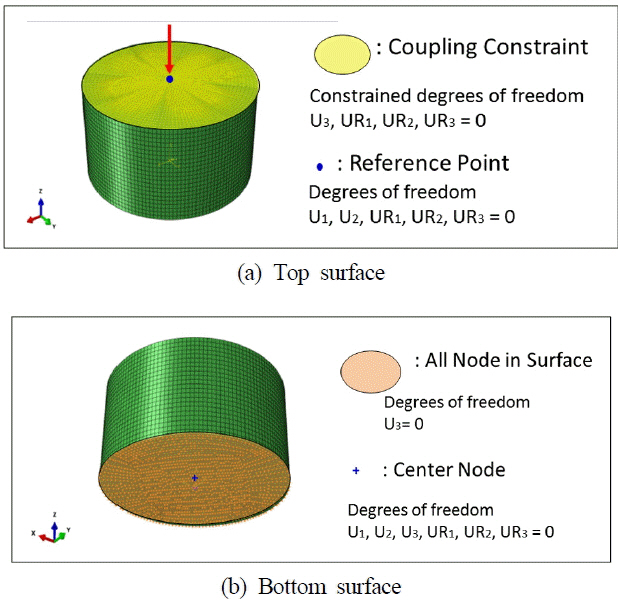
인장실험 해석모델은 수평방향을 x축, 수직방향을 y축, 시편의 두께 방향을 z축으로 설정하였다. 시편의 한쪽면을 고정하고 반대편에서 하중을 부여하는 실험조건을 모사하기 위하여 해석모델의 좌측 그립부는 완전고정조건을 부여하였으며 우측 그립부는 y, z방향을 고정하고 x방향으로 하중을 부여하였다. Fig. 8은 인장해석모델에 적용된 하중과 경계조건을 보여주고 있다.
또한 압축실험 모사를 위한 해석모델의 경계조건은 배불림 현상 방지등의 여러 실험조건을 고려하여 상부면에 커플링을 통하여 하중을 부여하였으며 바닥면은 z방향 자유도를 제외하고 모두 구속조건을 부가하였다. 단, 강체 운동을 방지하기 위하여 바닥면의 중앙노드에 완전고정조건을 부여하였다. Fig. 9는 압축해석모델에 적용된 하중과 경계조건을 보여주고 있다.
4. 실험-해석 연계 결과 분석
4.1 인장실험-해석
인장실험에 대하여 유한요소해석 결과와 실험 결과와의 연계분석을 위하여 5종의 비선형 재료모델을 적용하여 해석을 수행하였으며 분할된 4개의 변형률 구간(λ : 1.0, 2.0, 3.0, 3.9)에서의 변형에너지 오차 비교를 통하여 정확도를 분석하였다.
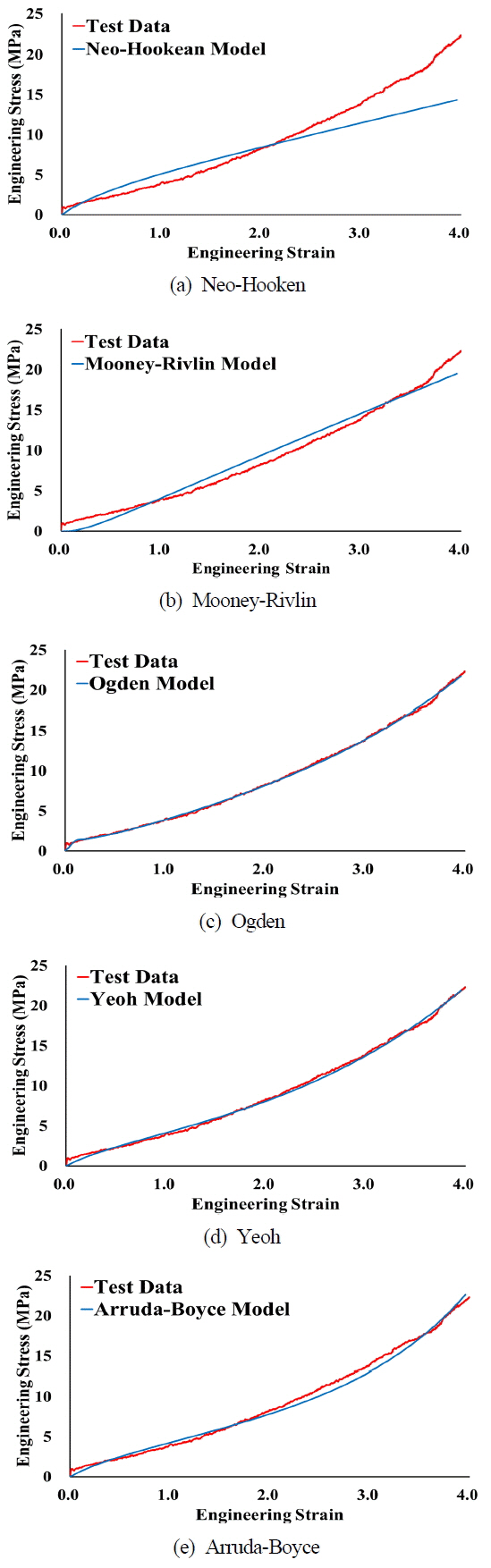
Table 7은 인장실험에 대하여 분할된 변형률 구간에서 해석과 실험결과에 대하여 변형 에너지 오차를 보여주고 있다. Neo-Hooken 모델의 각 분할된 변형률 구간에서의 변형 에너지 오차는 32.02%, 20.39%, 14.16%, 19.88%이다. 일반적으로 알려진 바와 같이 선형 특성을 갖고 있는 Neo-Hooken 모델은 신장률이 큰 변형을 충분히 모사하고 있지 못한 것을 확인 할 수 있다. Mooney-Rivlin의 경우, 각 구간별 29.49%, 19.01%, 13.32%, 8.93%의 오차를 보였다. 본 연구에서는 2차식의 Mooney-Rivlin 모델을 사용하였으며 고차식을 사용할 경우에는 보다 정확한 결과를 얻을 수 있을 것으로 판단된다. Ogden 모델의 경우, 각 구간별 3.38%, 2.19%, 1.52%, 1.37%의 오차를 보여주고 대변형을 잘 반영하는 것으로 알려진 것과 같이 400%의 연신률을 갖는 시편의 거동을 잘 모사하고 있음을 확인하였다. Yeoh 모델의 경우, 각 구간별 6.79%, 5.60%, 3.84%, 2.66%의 오차를 보여주고 있으며 Arruda-Boyce 모델의 경우 각 구간별 13.37%, 7.27%, 7.12%, 5.21%의 오차를 보여주고 있다. Fig. 10는 각각의 비선형 재료모델의 실험-해석 결과를 보여주고 있으며 Fig. 11은 Ogden 모델의 유한요소해석 결과이다. 인장실험의 경우, 시편으로 사용된 초탄성 재료가 갖는 변곡점의 특성을 잘 표현해 주는 재료모델은 Ogden 모델이며 이를 통하여 약 400%의 연신률을 갖는 초탄성 재료의 경우 Ogden 모델이 적절함을 확인하였다.
4.2 압축실험-해석
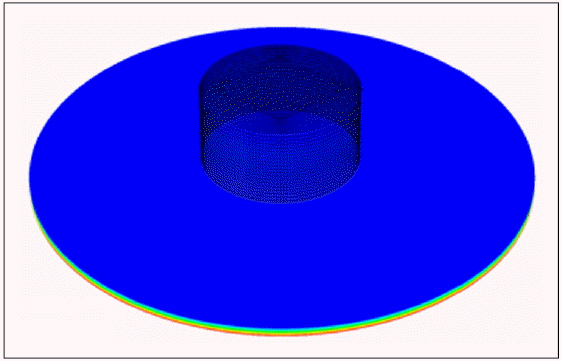
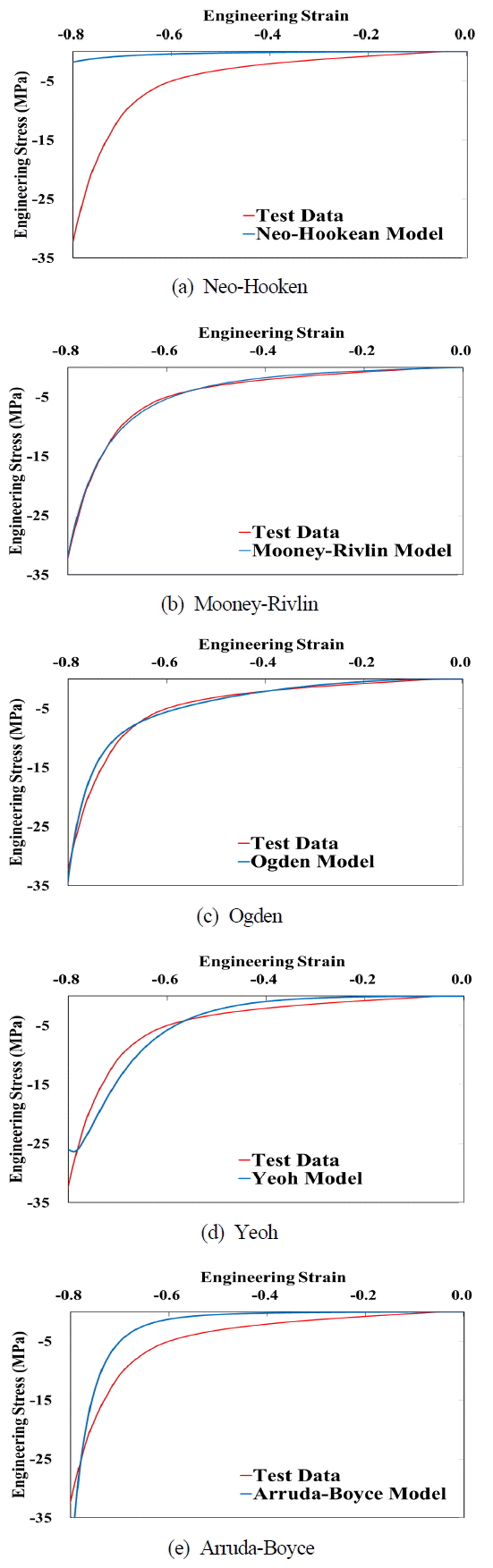
압축실험 해석과 실험결과의 연계분석도 인장실험 분석과 동일하게 5종의 비선형 재료모델을 적용하여 해석을 수행하여 분할된 4개의 변형률 구간(λ: -0.2, -0.4, -0.6, -0.8)에서의 변형에너지 오차를 비교하였다. 분할된 4개의 변형률 구간에서의 변형에너지 오차는 Table 8과 같으며 Mooney-Rivlin 모델의 유한요소해석 결과는 Fig. 12와 같다. 각각의 비선형 재료모델에 관한 실험-해석 결과는 Fig. 13에 나타내었다.
Neo-Hooken 모델의 경우, -2.0, -4.0, -6.0, -8.0의 각 구간에서의 오차는 0.19%, 92.40%, 92.02%, 93.01%였으며 인장실험-해석 비교 결과와 유사하게 큰 오차를 보여주고 있다. Mooney-Rivlin 모델의 경우는 각 구간별 29.34%, 23.97%, 12.35%, 5.30%의 오차를 보여주고 있다. Ogden 모델의 경우, 각 구간별 49.83%, 0.19%, 8.21%, 7.99의 오차를 보여주고 있으며 Yeoh 모델의 경우 88.96%, 74.95%, 38.70%, 11.86%의 오차를 보여주고 있다. 마지막으로 Arruda-Boyce 모델의 경우, 각 구간별 91.44%, 91.28%, 85.82%, 49.25%의 오차를 보여주고 있으며 전체 구간(λ= -0.8)에서 실험결과를 잘 모사하는 모델은 Mooney-Rivlin 모델임을 확인할 수 있다. 하지만, λ가 -0.4와 -0.6일 경우에는 Ogden모델이 더욱 잘 모사하는 것을 확인 할 수 있다. 이를 통하여 초탄성 재료의 운용 조건에 따라, 즉, 하중조건에 따라 해석에 사용되는 모델이 달라야 함을 확인 할 수 있었다.
5. 결 론
본 논문에서는 초탄성 재료의 해양플랜트 구조물 적용을 위하여 재료 특성실험에 관한 실험을 수행하였고, 인장 및 압축실험결과를 비선형 재료모델을 적용한 유한요소해석 결과와 비교하여 해석의 정확성 향상을 위한 연구를 수행하였다. 또한, 신장률에 따라 적합한 재료모델을 제안하였으며 이로부터 다음의 결론을 얻을 수 있다.
(1) 본 연구의 대상인 신장률 0~400%사이의 천연고무 기반의 탄성체는 인장실험의 경우에는 Ogden 모델이, 압축실험의 경우에는 Mooney-Rivlin 모델이 하중-변위응답, 응력-변형률응답에 가장 부합됨을 알 수 있었다.
(2) 비선형 재료모델은 하중조건(인장 또는 압축) 및 변형량에 따라 적합한 모델이 다름을 확인할 수 있었으며 정확한 해석 및 설계를 위해서는 재료의 운용조건에 대한 분석을 통하여 적합한 모델을 선택하여야 한다.
(3) 압축실험의 경우, 응력 연화 현상(Mullins effect)를 고려하여 반복 하중 부여를 통한 물성 안정화 과정이 필요하며 실험데이터는 보정 과정이 반드시 필요함을 알 수 있었다.
향후 해양플랜트 구조물의 운용환경을 고려하여 속도변화 및 온도조건 변화에 관한 효과를 반영하는 개선된 비선형 재료모델을 개발하는 것이 필요하며 요소망을 최적화하여 실험결과와 해석결과가 데이터베이스 형태로 연계된 정확도 향상 기법의 개발이 요구된다.