|
 |
- Search
| J. Ocean Eng. Technol. > Volume 32(6); 2018 > Article |
|
Abstract
In this study, a new numerical modeling system was proposed to predict oil spills, which increasingly occur at sea as a result of abnormal weather conditions such as global warming. The hydrodynamic conditions such as the flow velocity needed to calculate oil dispersion were estimated using a three dimensional hydrodynamic model based on the Navier-Stokes equation, which considered all of the physical variations in the vertical direction. This improved the accuracy compared to those estimated by the conventional shallow water equation. The advection-diffusion model for the spilled oil was combined with the hydrodynamic model to predict the movement and fate of the oil. The effects of absorption, weathering, and wind were also considered in the calculation process. The combined model developed in this study was then applied to various test cases to identify the characteristics of oil dispersion over time. It is expected that the developed model will help to establish initial response and disaster prevention plans in the event of a nearshore oil spill.
최근 들어 국제적인 교역량의 증가로 대형 선박의 입출항이 점점 증가하고 있는 사회적 여건의 변화로 인하여 해안 및 해양지역에서의 오염물질의 유출사고도 빈번하게 발생하고 있는 실정이다(Xie et al., 2017). 1995년 전라남도 여수에서는 선적 14만 톤의 유조선 씨프린스호가 암초에 부딪히면서 5천여 톤의 기름이 바다에 유출된 적이 있으며, 2007년에는 서해 태안 앞바다에서 홍콩 선적의 유조선 ‘허베이 스프릿 호’와 삼성물산 소속인 ‘삼성1호’가 충돌하면서 유조선 탱크에 저장되어 있던 1만 2,547킬로리터의 유류가 태안 인근 해역으로 유출되어 어업으로 생계를 꾸리던 지역민들에게 심각한 물질적〮/정신적 피해를 입혔다. 이 외에도 2010년 서산 대산항에서 유조선 탱크의 밸브를 잠그지 않아 한 시간 여 동안 기름이 유출된 바 있으며, 2014년에는 울산 에쓰오일 공장에서 탱크에 균열이 생겨 약 3만 배럴(4,767 킬로리터) 정도의 기름이 유출되는 사건이 있었다.
해외의 경우 2010년 멕시코 만의 딥워터 호라이즌 석유시추시설이 폭발하면서 5개월 정도 기름이 유출되어 인근 해역에 막심한 피해를 준 사건이 있었으며, 2014년 이스라엘의 에일라트 인근에 설치된 송유관에서 유출사고가 발생하여 5백만 리터 이상이 인근 지역으로 유출되었다. 인근 일본에서는 1997년1월2일 일본 후쿠이 현 일대에서 페트로파블로프스크로 향하던 러시아 유조선 나홋카호가 침몰하면서 6,200여 톤의 난방용 중유가 유출되었다. 사고 발생 직후 오사카 대학의 공학연구과에서는 프린스톤 대학에서 개발되어 널리 사용되고 있는 대표적인 3차원 해양순환 모델인 POM(Princeton ocean model)을 이용하여 유출사고를 모의하여 중유의 이동경로를 예측한 바 있다(Yohei et al., 2007).
이렇듯, 오일 등을 포함한 해양유출사고는 거의 매년 발생하고 있으며 한번 발생하면 생태계뿐만 아니라 인근 주민들의 생계와 직결되는 사안이어서 막대한 물적 자원 손실을 수반함과 동시에 회복하는데 짧게는 수개월에서 길게는 수년이 걸리는 중대한 사고이다. 따라서, 해양오염사고에 조기 대응하여 피해를 최소화 할 수 있는 방재 매뉴얼의 확립이 필요하며, 이를 위해 오염물질의 유출량과 해류 및 해상풍에 의한 이동범위의 정확한 예측이 필요하다. 정확한 예측모형 개발을 위해서는 해류를 정확도 높게 예측할 수 있는 모형의 사용이 선제적으로 이루어져야 한다.
유류유출 확산에 관한 연구는 지금까지 국내외적으로 다양하게 수행되었다. Lee et al.(2000)은 PIV(Particle Imaging Velocimetry) 계측법을 이용하여 유적의 거동을 정량화 할 수 있는 기법을 소개한 바가 있으며, Jung and Kim(2008)은 유한요소모형을 이용한 조류해석과 Random-Walk 모형 기반의 이송확산모형을 결합하여 해수유동 및 담수확산 예측시스템을 제시하였다. Kim(2011)은 선형파 이론에 근거한 해양파의 전파속도를 이용하여 파에 의한 기름확산 예측방법을 제시하였으며, Cho et al.,(2012)은 천수방정식과 이송확산방정식을 결합하여 대양에서의 유류확산을 모의하였다. 해외에서도 유류유출 관련하여 다양한 연구들이 수행되었다(Chao et al., 2001; Chao et al., 2003; Dominicis et al., 2013a; Dominicis et al., 2013b; Gong et al., 2014). 그러나 기존의 이러한 연구들은 이송확산에 필요한 유속을 구하기 위하여 수심적분된 2차원 모델을 사용하거나 정수압 가정의 3차원 모형을 사용하여 복잡한 유동의 3차원적 거동을 모의하는데 여러 가지 제약이 있었다.
본 연구의 목표는 3차원 동수역학모형과 유류유출모형을 결합하여 해양사고 시 유출되는 유류의 초기 확산을 예측할 수 있는 모형을 제안하고 이를 활용하여 유류유출사고 발생 시 유출량 및 해류/해상풍에 의한 확산 거동을 정확도 높게 예측하는 것이다. 이를 통해 예측결과에 기반을 둔 사고해역의 신속한 통제 및 처리가 가능하게 된다. 또한, 해양사고 조기대응을 통해 산업적, 환경적, 재산적 피해를 최소화하고 향후 유류유출사고 발생 시 효율적으로 대처할 수 있는 대응체계 구축기반을 마련하는데 활용할 수 있다.
우선적으로 해역에서 발생하는 유류유출의 이송확산을 정확도 높게 모의하기 위해서는 유속을 정확하게 계산하는 것이 선제적으로 이루어져야 한다. 즉, 유류 등의 해상 오염 물질은 특성상 흐름에 의해 지배적으로 이동, 전파 및 확산되므로, 파랑 및 조류의 영향을 많이 받고, 불규칙한 지형 변화가 존재하는 영역에서의 흐름예측은 유류의 확산을 예측하는데 매우 중요한 과정이라고 할 수 있다. 하지만 지금까지 유류유출을 해석하기 위한 유속모형은 수심적분된 천수방정식을 주로 사용하였다(Jung, 2009; Cho, 2014). 그러나 이러한 방정식의 사용은 다음과 같은 단점이 있다. 첫 번째로, 3차원 지배방정식을 단순화시키기 위하여 수심방향으로 적분을 하여 유속의 연직분포를 제대로 고려할 수 없다. 이는 연직 방향으로의 유속차이로 인하여 야기되는 다양한 순환현상을 모의할 수 없으며 수평방향 유속을 구함에 있어서도 정확도를 떨어뜨린다. 두 번째로, 천수방정식은 파의 중요한 특징 중에 하나인 분산성을 고려할 수 없다. 즉, 수심평균한 비분산성 흐름모형을 사용하여 파랑의 분산성이 무시되고 이로 인하여 오차를 포함하는 흐름조건을 산출되게 되므로 결과적으로 유류의 이송확산 예측의 정확도를 떨어뜨리게 된다. 이를 개선하기 위하여 파의 분산성을 모의할 수 있는 수심 적분형 Boussinesq 모형을 이용한 연구가 수행되었으나 여전히 수심적분된 모형의 한계를 가지고 있다(Son et al., 2009).
따라서, 본 연구에서는 이러한 단점들을 해결하고자 수심방향으로의 유속변화를 고려하고 복잡한 흐름특성(난류, 쇄파 등)을 모의할 수 있는 3차 수치모형을 유류유출 해석에 적용하고자 한다. 본 연구에서 사용하는 3차원 모형 NHWAVE(Ma et al., 2012)은 Navier-Stokes 방정식을 지배방정식으로 사용하며 다음과 같이 나타낼 수 있다.
여기서, (i, j)=1,2,3, x i *
여기서, h는 수심, D(h+η)는 σ-좌표계 변환을 위해 정의된 바닥부터 수면까지의 전체수심, η는 수면변위를 나타낸다(Ma et al., 2012). 따라서, 식 (1)과 식 (2)는 다음과 같이 나타낼 수 있다.
여기서,
또한, Sh, Sp, Sτ는 각각 수심변화, 압력 및 전단응력에 의한 소스항이며 Ma et al.(2012)에서 자세한 내용을 찾을 수 있다. 한편 자유수면 η는 다음과 같이 식 (4)를 σ=0부터 σ=1가지 적분하여 계산할 수 있다.
식 (4)-(5) 및 식 (6)에 유한체적법과 유한차분법을 적용하여 수치해를 구하였다. 압력값이 셀의 중앙에 위치하면 자유수면 경계조건을 정확하게 줄 수 없기 때문에 셀의 상단면에서 압력 값을 계산하였으며 나머지 변수들은 셀의 중앙에 위치한다고 가정하여 계산하였다. 모멘텀 방정식에는 2nd order Godunov-type 유한체적법을 적용하였으며 셀 면에서의 유량을 계산하기 위하여 HLL approximate Riemann solver를 사용하였다(Ma et al., 2012; Ma et al., 2013). 모멘텀 방정식을 풀 때 필요한 압력은 포와송 식을 사용하여 구하였으며, 파의 생성 및 경계처리는 내부조파 및 스폰지 경계층 개념을 사용하여 처리하였다(Larsen and Dancy, 1983)
해양의 경우 영역이 광범위하기 때문에 3차원 모형을 사용할 경우 계산에 상당히 많은 시간이 소요된다. 이를 극복하기 위하여 High performance preconditioner HYPRE software를 모델에 적용하여 MPI(Message passing interface)를 이용한 병렬처리가 가능하도록 하였다.
유동모델에서 계산한 유속과 해상풍 등을 결합하여 유류의 유출을 모의할 유류유출모형은 기본적으로 Lagrangian 좌표를 기반으로 한다. 이는 유류의 특성상 이송의 메커니즘이 유류입자의 이동으로 가정될 수 있기 때문이다. 해역에서 발생하는 유류의 이동 및 확산은 Eulerian 기반의 유동모델과 Lagrangian 기반의 유류유출모형의 결합을 통해 예측할 수 있다. 본 연구에서 유동모델과 결합할 유류유출모형으로 미국 Office of Response and Restorations(OR&R)의 Emergency response division에서 개발하여 사용 중인 GNOME(General NOAA operational modeling environment)을 사용하였다(Beegle-Krause, 2001; Zelenke et al., 2012). GNOME은 다양한 종류의 유류유출에 대해 이동, 확산, 증발 및 해안접착 등을 모의할 수 있도록 제안된 프로그램이다.
GNOME에서 유류입자의 이동(∆x, ∆y)은 해당시간 ∆t 동안의 유속 및 풍속 등에 의해 결정되며 1st order Runge-Kutta 방법을 이용하여 다음과 같이 계산된다.
여기서 111,120.00024는 위도 1도에 해당하는 미터 길이를 의미하며 어디서나 동일하다고 가정한다. 확산은 식 (9)와 같이 고전적인 확산방정식을 이용하여 모의한다.
여기서 C는 유류의 농도를 나타내며 Dx, Dy 는 각각 x, y방향의 확산계수를 의미하며 Random walk 이론에 기반을 하며 다음과 같이 구할 수 있다.
여기서,
결국 이로 인한 이동은 다음과 같이 계산된다.
유류의 이동과정에서 발생하는 증발(또는 풍화)은 다음의 식을 이용하여 모의한다.
여기서, Pi는 유류를 구성하는 각 성분의 구성 비율을 의미하고 Hi는 각 성분의 반감기를 의미하며 각각의 유류에 대해 다음 Table 1과 같이 주어진다.
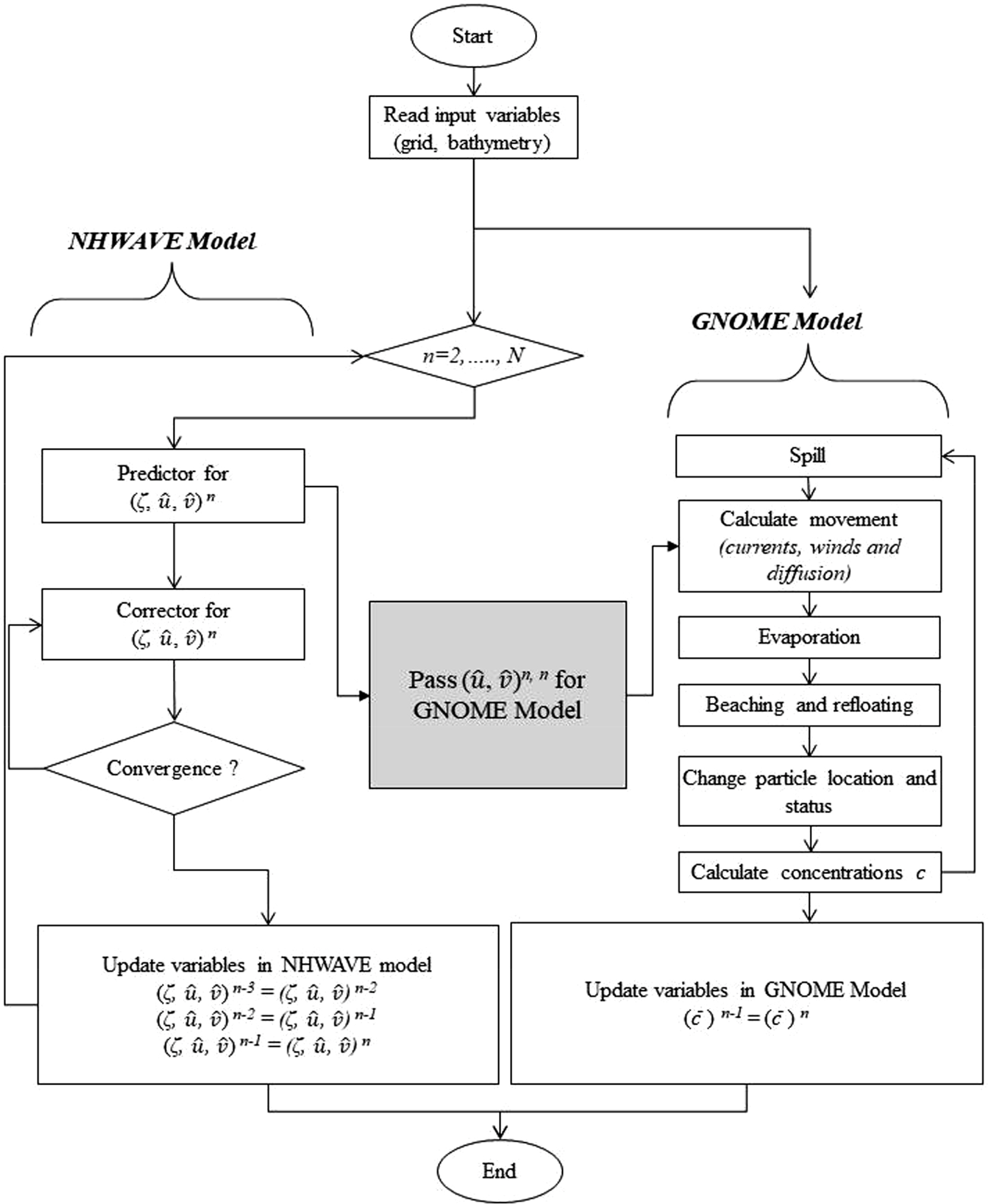
해역의 흐름특징을 대표할 수 있는 유속정보와 오염물질의 대표적 사례인 유류를 대상으로 하여 유류유출시 유류의 이송확산을 예측할 수 있는 모형을 개발할 수 있다. 본 연구에서는 3차원 수치모형과 유류유출모형간의 외적 결합을 통하여 결합모형을 구축하고자 한다. 즉, 해역에서 파랑에 의한 흐름은 3차원 수치모형으로 예측하고 그 결과를 유류유출모형의 입력값으로 사용하여 유류가 이송 및 확산되는 양상을 모의하게 되는 것이다. 다만, 두 모형의 기본 좌표계가 각각 Eulerian과 Lagrangian으로 다른 형태를 지니기 때문에 이들 상호간의 정확한 위치에서의 정보가 공유되기 위한 면밀한 고려가 필요하며, 이를 통해 외적 결합이 성공적으로 이루어 질 수 있을 것이다. Fig. 1은 이들 두 모형이 이론적으로 결합되는, 즉 정보를 교환하는 순서를 나타내며, 최종적으로 유류의 이송과 변형상태 등을 모의결과로 보여준다. 이를 순서대로 설명하면 3차원수치모형에서 예측자-확인자 수치해석방법으로 3차원 유속정보가 산출되면 이를 수심적분하여 수평방향 평균유속을 산출한다. 이는 Eulerian 좌표에서 산출된 정보이므로 이를 Lagrangian 좌표계로 변환한 후, 유류유출모형에 전달되며 전달된 유속정보와 그 외의 입력조건(해상풍, 유출유의 종류, 유출량 및 유출시간)과 결합하여 유류 입자의 이송-확산-증발 과정을 계산하게 된다.
본 연구에서는 파랑에 의해 유발되는 해류에 초점을 맞추었기 때문에 파랑의 복합적인 메커니즘이 잘 재현되는 지형에 대해 3차원 수치모형을 적용하였다. 첫 번째는 이상적인 Rip channel에 적용하여 해안에서 복잡한 물리적 현상과 맞물려 발생하는 이안류를 모의하였으며 이 상황에서 유류유출이 발생할 경우 유류의 이동 및 확산 현상을 해석하였고, 두 번째로는 실해역을 대상으로 실제 파랑조건을 사용하여 해류의 거동 및 이로 인한 유류의 이동 및 확산을 모의하였다.
먼저 해안에서 발생하는 대표적인 현상인 이안류에 대한 유출유류의 이동 및 확산을 모의해 보았다. 이안류란 여러 가지 요인(Dalrymple et al., 2011)에 의해 발생하는 연안에서 원해로의 흐름을 의미하며 우리나라에서는 부산 해운대에서 매년 하절기에 발생하여 각종 인명사고를 유발하고 있다. 이안류는 인명과 관련된 문제뿐만 아니라 해안선을 따라 흐르는 연안류와 함께 해안에서 발생하는 각종 침/퇴적 현상과도 밀접한 관련이 있어 이와 관련된 다양한 연구가 활발하게 진행되고 있다.
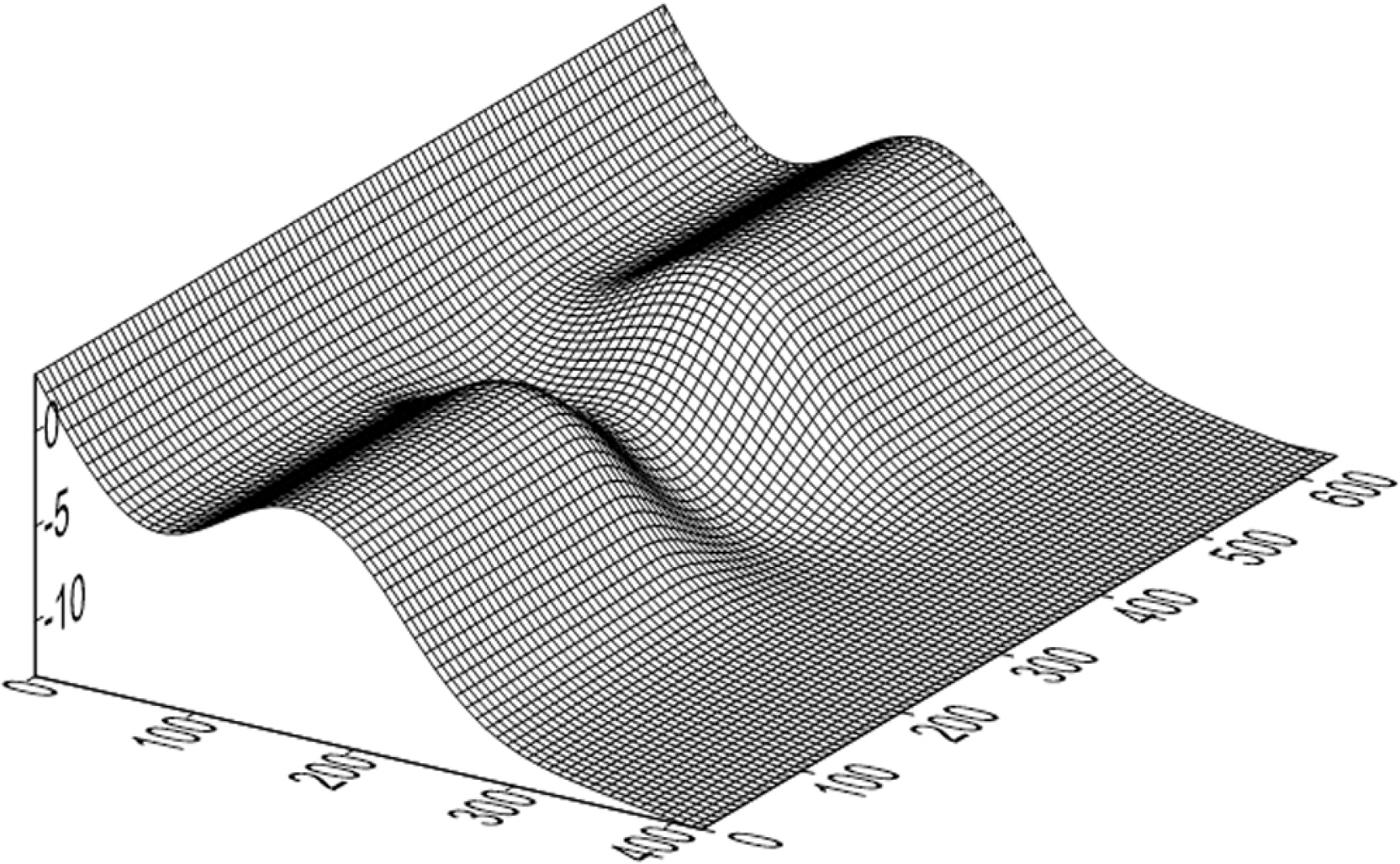
인위적으로 이안류를 발생시키기 위하여 Fig. 2와 같이 지형을 만들어 수치모의에 사용하였다. 그림에서와 같이 양쪽의 수심이 얕은 지형은 이안류를 발생시키기 위해 자주 사용하는 지형으로 수심이 얕은 양쪽 부분에서 천수 현상에 의해 파고가 증가하며 이렇게 증가된 파고는 불안정성이 더해져서 쇄파하게 된다. 이렇게 파가 부서지게 되는 경우 파랑의 Radiation stress에 의해 연안방향으로 과도한 힘이 발생하게 되는데 이로 인해 연안지역에서는 수체 및 에너지 흐름간의 불균형이 발생하여 바다에서 육지쪽으로 흐름이 발생한다. 이렇게 축적된 수체는 다시 가운데 수로를 따라 외해로 나가게 되는데 이러한 현상이 이안류의 대표적인 메커니즘이다.
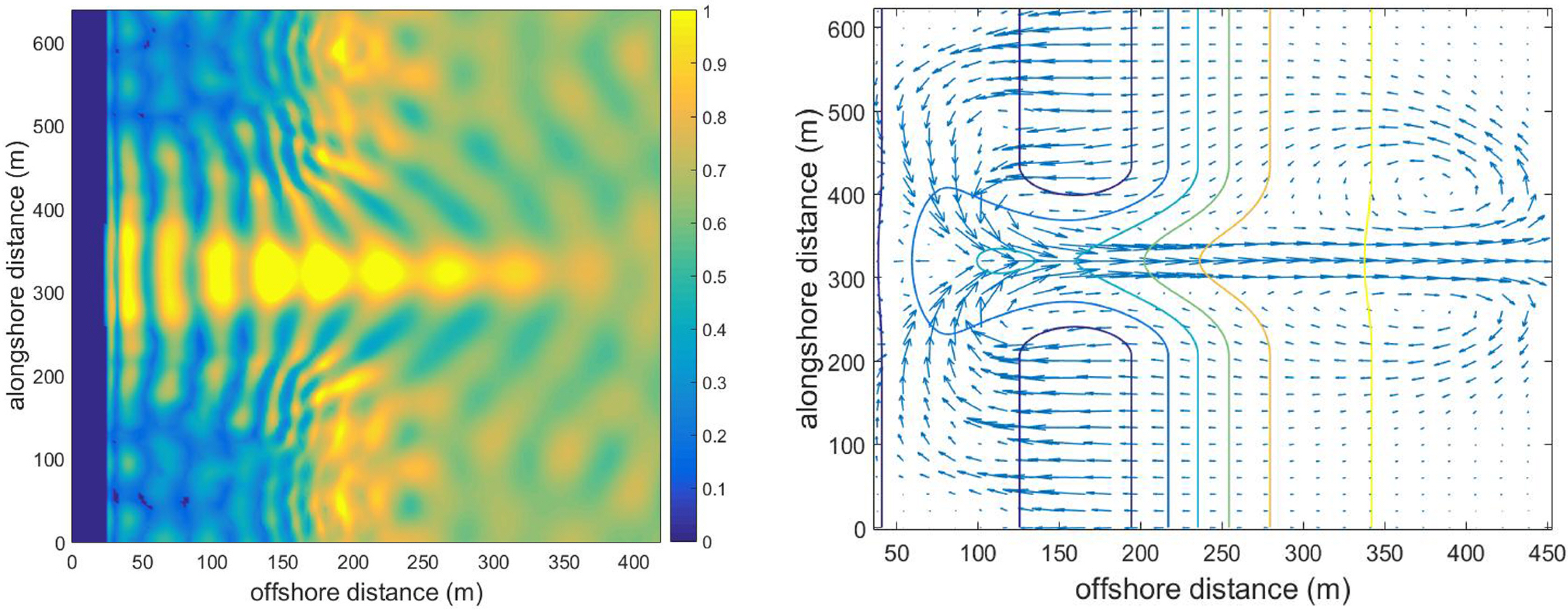
Fig. 3은 Rip channel 지형에 대해 수치 모의한 결과이다. 파고 분포를 보면 앞서 기술한 바와 같이 수심이 얕은 양 옆에서 쇄파(파가 부셔지는 현상)에 의한 에너지 감소로 파고가 감소하는 것을 확인할 수 있다. 또한, 이 때 발생한 Radiation stress로 인하여 양 옆에서는 해안쪽으로 흐름이 발생하였으며 가운데에서는 외해 방향으로 흐름이 발생하는 것을 확인할 수 있다.
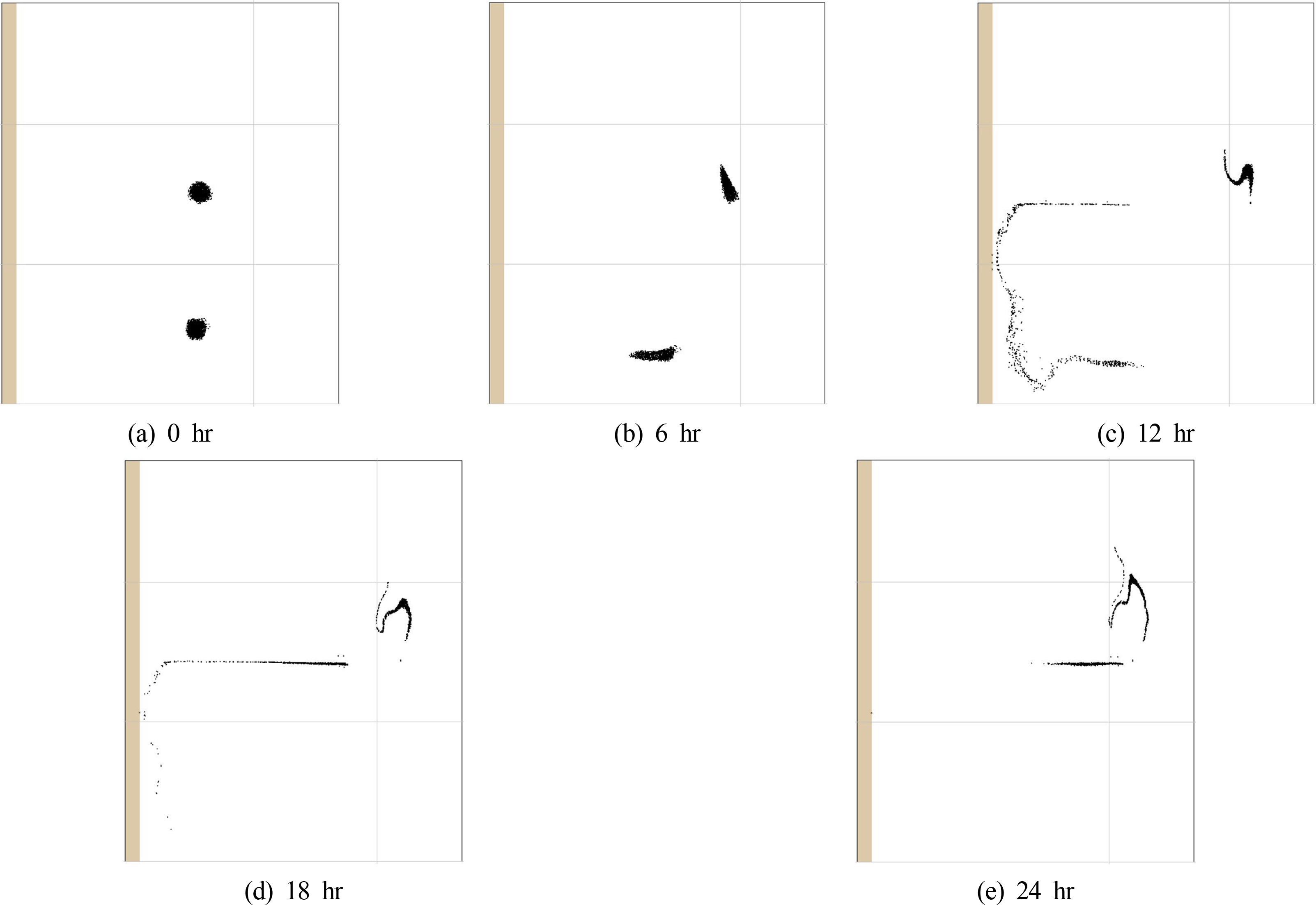
이와 같은 지형에 유류유출 사고가 발생할 시 이안류에 의한 유류의 이동 및 확산을 검토해 보았다. 전 영역에 걸쳐 유류의 이동을 모의하기 위하여 Fig. 4(a)처럼 100배럴(약 16,000리터)의 오일을 선형으로 분포시킨 후 모의한 후 6시간 간격으로 유류의 이동결과를 나타내었다. 이 때, 바람의 효과는 무시하였으며 증발은 없는 것으로 가정하였다. Fig. 3의 유속결과와 비교해보면 유류의 이동이 유속에 절대적으로 영향을 받는 것을 확인할 수 있다.
다음으로 다양한 유류의 종류에 따른 이동 및 확산의 양상을 모의 및 분석해보았다. Table 1을 보면 유류의 종류에 따라 구성 성분의 반감기가 다르다는 것을 알 수 있다. Gasoline은 세 성분 중에서 두 성분의 반감기 시간이 매우 짧아 증발현상이 잘 일어난다는 것을 알 수 있으며, Diesel은 48시간 이내에 75%의 성분이 절반이 된다는 것을 알 수 있다. 따라서 이번 해석에서는 반감기가 없는 경우와 Gasoline 및 Diesel에 대해 24시간 동안의 유류의 이동을 모의하였다. 그 결과, 증발현상이 전혀 발생하지 않은 Fig. 5(a)와 비교해보면 Fig. 5(b)에 나타난 Gasoline의 경우 상당히 많은 양이 사라진 것을 확인할 수 있다.
다음으로 유류의 이송확산에 대한 바람의 영향을 알아보았다. 바람의 방향을 모두 고려할 경우 계산 경우 및 결과분석이 과도하게 복잡해지기 때문에 본 연구에서는 육지방향으로 일정한 바람이 부는 경우로 한정하였으며 바람의 크기는 유속의 크기와 비슷한 정도, 약간 큰 정도, 매우 큰 정도로 구분하여 모의하였다. Fig. 3에서의 유속분포를 보면 유속이 큰 경우에는 O (0.1)m/s를 가지며 유속이 작은 양 옆에서는 O (0.01)m/s 정도를 가진다. 따라서 풍속은 동쪽에서 서쪽방향으로 0.1m/s, 0.5m/s, 1.0m/s를 가정하였다. Fig. 6은 풍속의 세기에 따라 유류유출 24시간 후의 이송확산 차이를 보여준다. 결과에서도 알 수 있듯이 유속에 준하는 경우에는 이송확산에 제한적인 영향이 있으나, 유속에 상응하거나 그보다 강한 풍속이 존재할 경우 풍속이 지배적으로 이송확산을 유발시켜, 유속의 영향이 제한적으로 작용함을 알 수 있다.
이상적인 지형에서 3차원적으로 발생하는 연안수리현상을 성공적으로 재현하고 이에 의한 유류유출현상도 연계하여 모의함으로써, 연계모형의 성능을 평가하였다. 다음으로 동해안에 위치한 실제 지형에 대해 유류의 이송 및 확산을 모의하여 실용성에 대한 검증이 이루어졌다. 대상 지역은 강원도 고성군에 위치한 천진항으로 주머니 형태의 해안선을 취하고 있어 이안류 및 연안류의 복잡한 거동이 나타나는 특성이 있다. Fig. 8은 대상지역에 대해 관측 및 수치모의한 결과를 보여준다. 왼쪽은 실제 흐름을 관측하기 위한 Buoy를 설치하여 그 이동경로를 표시한 그림이다. 총 6개의 Buoy를 설치하였으며 검은 점은 시작 지점, 빨간 점은 종착 지점을 나타낸다. 우측은 3차원 수치모형을 이용하여 모의한 결과이며 입력한 유의파고, 유의주기 및 입사각은 각각 0.89m, 7.3s 및 64.3°이다. 빨간색 원으로 표시한 지역은 이안류가 발생하는 지역이며 P1 및 P2는 각각 이안류 및 연안류가 지배적인 지점을 나타낸다. 수치모의한 결과를 보면, 상단 및 하단부에서 주머니형태의 안쪽으로 흐름이 발생하고, 이러한 흐름은 해안선을 따라 진행하다 특정 지점에서 외해로 빠져나갔으며 이러한 흐름 특성은 관측치와도 잘 일치하였다.
앞서 해석한 바와 유사하게 흐름에 의한 유류의 이동 및 확산을 전체적으로 살펴보기 위하여 Fig. 9와 같이 선형적으로 유류를 분포시킨 후 모의한 결과를 6시간 간격으로 나타내었다. 초기에 유출된 유류의 양은 100배럴로 가정하였으며 증발 및 바람의 효과는 우선적으로 고려하지 않았다.
다음으로 바람의 영향에 대해 살펴보았다. Fig. 10은 해당 지역에서의 바람 특성을 나타낸다. 약 2.4m/s 의 평균풍속을 지니고 있음을 알 수 있으며, 이를 기초로 풍속의 입력값을 정하여 유류의 이동을 모의하였다. GNOME에서 바람에 의한 이동은 풍속의 3%를 기본값으로 사용하고 있다. 주어진 영역에서 유속의 크기를 비교해보면 x 및 y 방향의 최대 유속은 각각 0.5306m/s 및 0.5138m/s가 되어 풍속에 의한 효과보다 크게 나왔으나 지속적으로 바람이 부는 경우에는 바람에 의한 영향이 지배적이 되어 Fig. 11에서 보는 바와 같이 대략 6시간 후에는 대부분의 유류가 육지에 접착되어 있는 것을 확인할 수 있었다.
다음으로 선형이 아닌 지점별로 유류가 유출되었을 경우에 대하여 모의해 보았다. Fig. 12에서 보는 바와 같이 이안류와 연안류가 지배적인 세 지점에 대해 각각의 지점에서 100배럴의 유류(약 16,000리터)가 유출된다고 가정하였고, 증발 및 바람에 의한 효과는 고려하지 않았다. 마지막으로 지점별 유류유출에 바람의 효과를 추가적으로 고려한 경우에 대해 살펴보았다. 앞선 경우와 동일하게 NE 방향에서 2.4m/s의 바람이 불어온다고 가정하여 그 결과를 Fig. 13에 나타내었다. 앞서 기술한 바와 유사하게 바람의 크기가 유속의 크기에 비해 매우 크기 때문에 유출 초기부터 바람의 영향을 지배적으로 받는 것을 확인할 수 있었으며, 대략 6시간 정도 지났을 때 대부분의 유류가 육지에 접착되어 있는 것을 확인할 수 있다.
본 연구에서는 최근 발생빈도가 잦아지고 있는 유류유출사고에 대비하여 해수의 3차원 연직흐름 특성, 비선형적 파랑거동 및 유류 유동을 종합적으로 고려한 수치해석모형을 제안하였다. 해수 유동과 관련해서는 해수의 연직특성을 고려하면서 파랑으로 인해 야기되는 다양하면서 복잡한 거동 등을 모의할 수 있는 3차원 수치모형을 이용함으로써 기존 모형이 지닌 문제점을 개선하고자 하였으며, 유류의 화학적 특성을 동시에 고려하여 기존에 발생한 유출사고와의 비교를 통해 각 종 계수들을 보정한 정도 높은 유류유출모형을 사용하여 신뢰할만한 모델을 제시하였다. 제안된 모형은 유류의 증발, 풍화작용뿐 아니라 해상풍 등 유류 자체의 성질 이외의 영향을 고려하였으며 유속모델을 통해서는 파랑의 분산성, 비선형 및 복잡한 지형에서의 연직방향 흐름특성까지 고려함으로써 해석결과의 신뢰성을 제고하고자 하였다.
제시된 모형을 다양한 흐름 특성이 있는 지역에 적용해 본 결과, 유속이 큰 지역에서는 이송에 의해 유류의 이동이 활발하였으며 유속이 상대적으로 작은 지역에서는 확산의 효과도 유류의 이동에 제한된 정도의 기여를 하였다. 유류의 종류에 따라 Gasoline과 같이 증발성이 강한 유류는 유출 초반부에 많은 양들이 증발하여 실제 이송 및 확산되는 양이 많지 않았다. 또한 Fig. 5에서 보여준 바와 같이 유종에 따라 기본 성질인 비중, 점도 뿐 아니라 증발성에 따라 이송 및 확산의 양상이 달라질 수 있으며 유출유의 확산범위에 따라서도 증발양상이 다르게 나타므로, 다양한 유종을 종합적으로 고려한 후속연구를 통해 유류유출 및 거동에 대한 이해도를 높일 수 있을 것이다. 풍속의 영향에 대해서는 유류의 이송에 1% ~ 4%정도 제한적으로 영향을 준다고 알려졌으나 풍속의 크기가 유속과 비슷하거나 그 이상이 될 경우 지배적인 영향을 끼쳐 육지 방향으로 강한 바람이 불 경우 대부분의 유류가 해안에 접착되는 것을 확인하였다.
후기
본 연구는 행정안전부 재난안전기술개발사업단 연구사업(MOIS-재난-2015-03)과 기상청 기상⋅지진 See-At 기술개발 연구사업(KMI 2018-09510)의 지원으로 수행되었습니다.
Fig. 4.
Simulated advection and diffusion of oil spill over rip channel for 48 hours (Horizontal and vertical extent of domain are 560 m and 640 m, respectively.)

Fig. 6.
Simulated advection-diffusion results considering various wind gust conditions (after 24 hours)
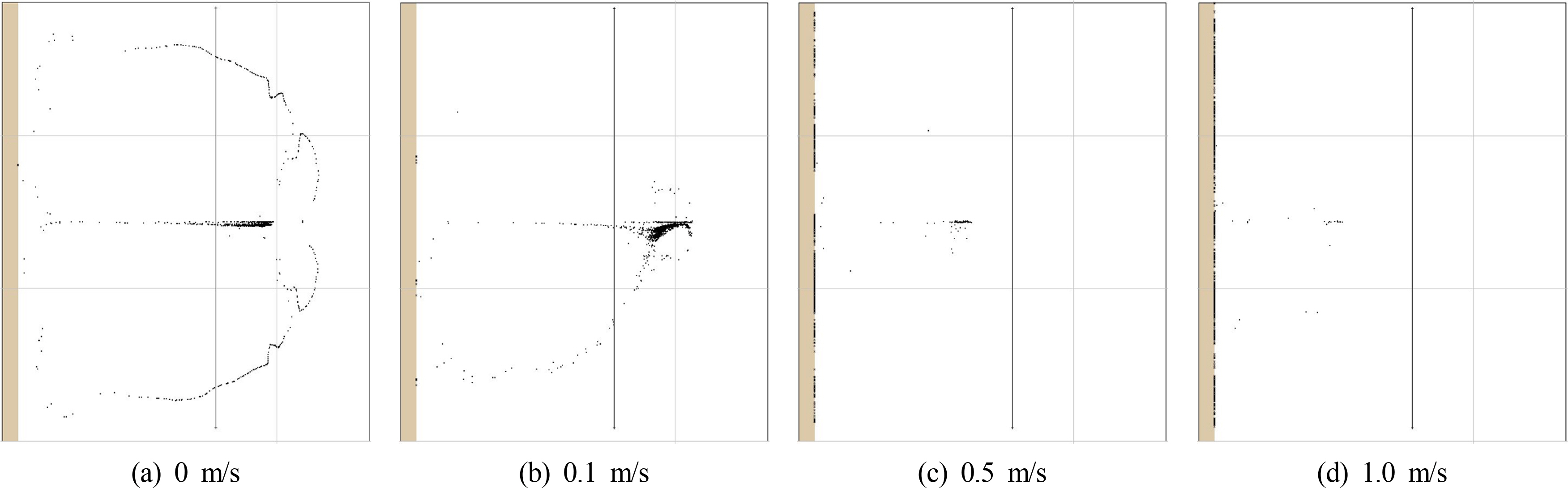
Fig. 8.
(Left) Observation points of buoy at Cheonjin Port and (Right) simulated current speeds (Horizontal and vertical extent of domain in right figure are 700 m and 800 m, respectively.)

Fig. 9.
Simulated advection-diffusion results of oil spill with linear distribution at Cheonjin Port (Horizontal and vertical extent of domain are 1160 m and 1300 m, respectively.)
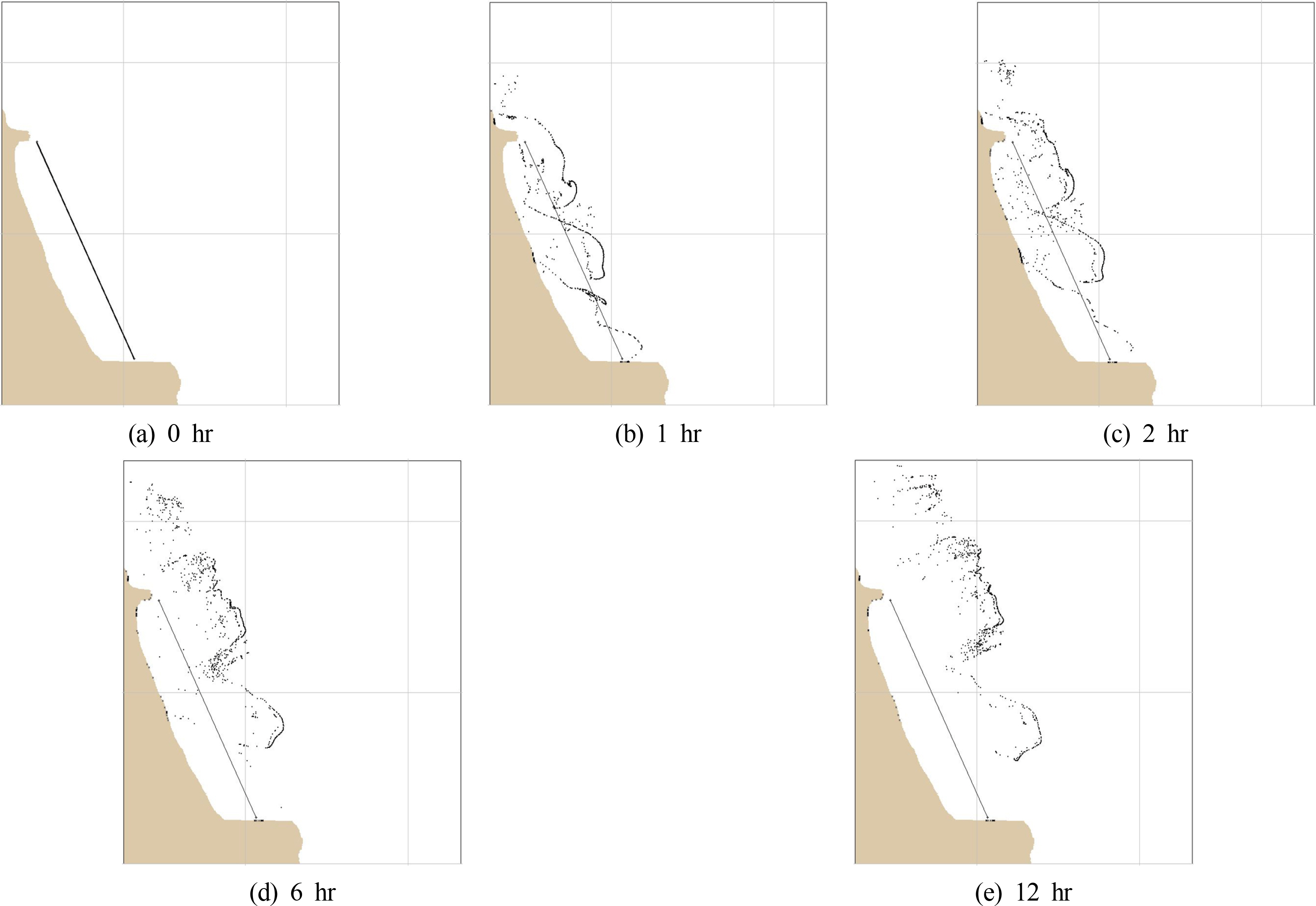
Fig. 11.
Simulated advection-diffusion results considering various wind gust conditions at Cheonjin Port

Fig. 12.
Simulated advection-diffusion results of oil spill from three point-sources at Cheonjin Port

Table 1.
Half-life of various pollutant materials depending on the ratio of constituents (Boehm et al., 1982)
References
Kim, Y-B. (2011). Study on Prediction for Prompt Countermeasures to Oil Spread in Ocean. Journal of Ocean Engineering and Technology, 25(2), 108-112.

Beegle-Krause, J. (2001). General NOAA Oil Modeling Environment (GNOME): A New Spill Trajectory Model. Proceedings of International Oil Spill Conference(IOSC), 2001(2), 865-871.

Boehm, PD., Feist, DL., Mackay, D., & Paterson, S. (1982). Physical- Chemical Weathering of Petroleum Hydrocarbons from the Lxtoc I Blowout: Chemical Measurements and a Weathering Model. Environmental Science and Technology, 16(8), 498-505.

Chao, X., Shankar, NJ., & Cheong, HF. (2001). Two- and Three-dimensional Oil Spill Model for Coastal Waters. Ocean Engineering, 28, 1557-1573.

Chao, X., Shankar, NJ., & Wang, SY. (2003). Development and Application of Oil Spill Model for Singapore Coastal Waters. Journal of Hydraulic Engineering, 129(7), 495-503.

Cho, Y-S. (2014). A Numerical Study on the Spread of a Pollutant in a Coastal Environment. Energy Sources, Part A: Recovery, Utilization and Environmental Effect, 34(16), 1459-1470.

Cho, Y-S., Kim, T-K., Jeong, W., & Ha, T. (2012). Numerical Simulation of Oil Spill in Ocean.. Journal of Applied Mathematics, ID 681585 1-15.

Dalrymple, RA., MacMahan, JH., Reniers, JHM., & Nelko, V. (2011). Rip Currents. Annual Review of Fluid Mechanics, 43, 551-581.

Dominicis, MD., Pinardi, N., Zodiatis, G., & Lardner, R. (2013a). MEDSLIK-II, A Lagrangian Marine Surface Oil Spill Model for Short-Term Forecasting – Part 1: Theory. Geoscientific Model Development, 6, 1851-1869.

Dominicis, MD., Pinardi, N., Zodiatis, G., & Archetti, R. (2013b). MEDSLIK-II, A Lagrangian Marine Surface Oil Spill Model for Short-Term Forecasting - Part 2: Numerical Simulations and Validations. Geoscientific Model Development, 6, 1871-1888.

Gong, K., Tkalich, P., & Xy, H. (2014). The Numerical Investigation on Oil Slick Behavior Behind the Oil Boom. Journal of Environmental Protection, 5, 739-744.

Jung, TS., & Kim, TS. (2008). Prediction System of Hydrodynamic Circulation and Freshwater Dispersion in Mokpo Coastal Zone. Journal of the Korean Society for Marine Environmental Engineering, 11(1), 13-23.
Jung, TS. (2009). Numerical Simulation of Spilled Oil Dispersion in Taean Coastal Zone. Journal of the Korean Society for Marine Environmental Engineering, 12(4), 264-272.
Larsen, J., & Dancy, H. (1983). Open Boundaries in Short Wave Simulations - A New Approach. Coastal Engineering, 7, 285-297.

Lee, JW., Doh, DH., Kim, KS., & Kang, SY. (2000). Development of Simulation Model for Diffusion of Oil Spill in the Ocean (III) - Oil Droplet Spreading Measurement Using 3-Dimensional Digital Image Processing Technique. Journal of the Korean Society of Marine Environment & Safety, 6(1), 47-55.
Ma, G., Shi, F., & Kirby, JT. (2012). Shock-capturing Non-hydrostatic Model for Fully Dispersive Surface Wave Processes. Ocean Modelling, 43-44 22-35.

Ma, G., Shi, F., & Kirby, JT. (2013). Numerical Simulation of Tsunami Waves Generated by Deformable Submarine Landslides. Ocean Modelling, 69, 146-165.

Son, S., Lynett, P., & Kim, D-H. (2009). Nested and Multi-physics Modelling of Tsunami Evolution from Generation to Inundation. Ocean Modelling, 38, 96-113.

Xie, C., Deng, J., Zhuang, Y., & Sun, H. (2017). Estimating Oil Pollution Risk in Environmentally Sensitive Areas of Petrochemical Terminals Based on a Stochastic Numerical Simulation. Marine Pollution Bulletin, 123(1–2), 241-252.


Yohei, M., Naozou, K., & Yuichi, M. (2007). Oil Spill Simulation of Nahotoka Accident with Princeton Ocean Model. Proceedings of the Japan Society of Naval Architects and Ocean Engineers Conference, 4, 135-138.
Zelenke, B., O’Connor, C., Barker, C., Beegle-Krause, CJ., & Eclipse, L. (2012). General NOAA Operation Modelling Environment (GNOME) Technical Documentation.. U.S. Department of Commerce, NOAA Technical Memorandum NOS OR&R 40: 105.
- TOOLS
-
METRICS

-
- 1 Crossref
- Scopus
- 4,546 View
- 85 Download
- Related articles in JOET
-
Numerical Simulation of Three Dimensional Free Surface Flow1990 June;4(1)