|
 |
- Search
| J. Ocean Eng. Technol. > Volume 33(2); 2019 > Article |
|
Abstract
Unlike typical a dynamic positioning (DP) system, a DP-assisted mooring system must determine a set point (SP) that can ensure a mooring tension safety range to prevent an excessive increase in mooring tension. In this paper, a new algorithm for determining the SP is suggested in order to reduce the tension on all the mooring lines. To determine the SP, a working area around the vessel is represented by a rectangular grid. Thus, the size of the grid area is limited considering the offset of a vessel with a mooring system. At each grid’s nodes, the resultant tension from all the mooring lines is estimated using the time history of the tension and vessel’s position. The results of static analyses for each grid position are used to estimate the global tension. Consequently, the SP is automatically selected as a position satisfying criterion for minimizing the total tension. In order to validate the suggested algorithm, a motion simulation with the control system in the time domain and a discussion of the results are presented.
해양에서 운용되는 부유식 해양 구조물의 위치유지는 계류선을 이용한 계류시스템과 추진기의 추력을 이용한 동적 위치유지 시스템인 DP(Dynamic positioning) 시스템이 일반적으로 사용되고 있다. DP보조계류시스템(DP assisted mooring system)은 계류시스템과 DP시스템을 결합한 형태로써, 극한의 환경조건에서 계류시스템만으로는 위치유지 기능을 적절히 수행할 수 없을 때, 독립적인 위치유지시스템보다 우수한 위치유지성능을 제공한다. 또한 DP보조계류시스템의 적용은 깊은 수심에 설치된 부유식 해양 구조물의계류선에 과도한 무게상승이 유발될 경우 재료로 인한 부하를 줄일 수 있다는 장점이 있다. Ryu and Kim(2003)은 수심이 매우 깊은 지역 및 극한의 환경을 견뎌야 하는 영구적인 플랫폼에는 단독적인 DP시스템을 사용하는 것보다 DP보조계류시스템을 사용하는 것이 합리적임을 보였다.
이러한 DP보조계류시스템은 단독적인 DP시스템과 달리 계류선의 장력을 고려하여 제어 목표점인 Set point(SP)를 선정하는 것이 필요하다. 따라서 안전한 생산활동을 보장하기 위하여 SP는 계류시스템의 장력과 구조물의 위치를 안전 범위 내에 유지시킬 수 있는 위치가 되어야만 한다(Nguyen and Sørensen, 2009a).
Barth Berntsen et al.(2008)는 계류선의 신뢰도지수(Reliability Index)를 이용하여 지속적으로 신뢰도지수를 허용 범위에 유지시킬 수 있는 SP 제어법을 제안하였다. 이 방법을 사용한 제어는 신뢰도지수를 사용하여 계류시스템의 안전을 직관적으로 제어할 수 있지만 장력의 동적인 요소에 의한 순간적인 구조물의 위치변화 및 장력변화를 고려할 수 없다는 단점이 있다.
Nguyen and Sørensen(2009b)는 SP 설정법을 일반적인 환경과 거친 환경으로 나누어 설명하고 있으며 특히, 거친 환경에서 계류 시스템의 파단을 방지하기 위한 목적으로 SP를 초기 위치에 가깝게 설정해야함을 강조하였다. 이 방법의 경우 계류시스템의 안전은 보장할 수 있으나 과도한 연료 소모를 유발할 수 있는 가능성이 존재한다.
본 연구에서는 SP를 설정하기 위하여 구조물의 위치와 장력 변화량을 이용한 장력 추측방법을 제안하였다. 장력이 가장 적을 것으로 예상되는 위치를 SP로 설정하는 전략을 구상하였으며 장력 추측을 위한 방법으로 국소장력과 전역장력을 함께 고려하는 방법을 제안하였다. 국소장력은 현재와 과거의 구조물 위치 및 장력을 이용하여 수식을 통해 계산되었으며 전역장력은 구조물과 계류시스템의 정적 해석을 수행하여 산출되었다. 최종적으로, SP는 두 요소의 중첩에 의해 결정되었으며 시뮬레이션을 통하여 본 연구의 결과를 입증하였다.
국소장력은 장력 추측을 위해 사용된 요소 중 하나이며 구조물의 위치 변화에 따른 장력 변화량을 기반으로 구조물이 주변 위치로 이동하였을 때 예상되는 장력의 변화량을 추측한 값이다. 국소장력을 이용하여 장력의 증가 및 감소 방향을 추측할 수 있으며 SP 선정을 위한 방향성 제시를 위하여 사용되었다.
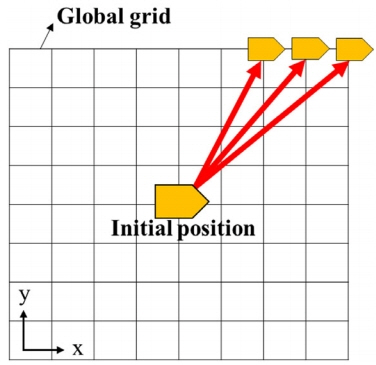
국소장력은 국소격자라는 영역을 기반으로 계산되었다. 이처럼 본 연구에서는 구조물의 활동 범위를 격자로 나타내었다. 전역격자는 Fig. 1에 실선으로 명시한 격자이며 격자의 중심위치는 구조물의 설계 위치를 나타낸다. 국소격자는 Fig. 1에 빗금으로 표시된 격자이다. 국소격자는 이동하는 구조물의 현재위치 중심으로 형성되기 때문에 이동에 따라 업데이트되는 격자이다. 두 종류의 격자 크기는 계류시스템의 와치서클(Watch circle)을 고려하여 설정하였다. 이는 SP로 선정될 수 있는 위치를 와치서클 내로 제한하여 위치제어 과정에서 발생할 수 있는 계류시스템의 과도한 장력상승을 방지하기 위한 목적이다.
계류시스템의 장력 변화를 이동거리에 대한 선형으로 가정하면 식 (7)을 통해 구조물이 과거의 위치에서 현재의 위치까지 이동한 단위거리 당 장력변화량을 정의할 수 있다. 국소장력계산과정은 정의된 위치와 장력 변화량을 기반으로 국소격자의 모든 위치에서 장력을 계산하는 과정이다. 따라서 식 (7)의 단위 장력변화량인 Unit Tx, Unit Ty에 국소격자의 위치와 과거 구조물위치의 편차를 곱하면 국소격자의 각 위치에서의 장력을 추측할 수 있다. Fig. 1에 점으로 명시된 국소격자의 임의 위치를 (x', y')로 가정하면 위치 편차는 식 (8)과 같이 계산될 수 있다. 식 (9)를 통해 위치편차인 (∆x', ∆y')를 단위 장력변화량에 곱하면 해당 격자 위치에서의 장력인 (Tx, Ty)'n를 추측할 수 있다. 추측된 x, y방향의 장력은 식 (10)에 따라 합산하여 한 계류선에 대한 국소장력으로 사용되었다. 본 연구에서는 예측된 장력의 크기가 아닌 증감경향을 보기 위하여 식 (10)과 같이 x, y방향의 장력을 합산하였다. 식 (10)까지는 국소격자의 한 위치에서 하나의 계류선에 대한 장력추측과정이다. 따라서 식 (10)의 장력은 계류선의 개수만큼 반복 계산되며 각 계류선마다 계산된 장력은 최종적으로 식 (11)을 이용하여 합산되었다. 본 연구에서 SP는 구조물의 생존이 아닌 생산활동의 효율 증대를 위한 장력 감소를 목적으로 하고 있다. 따라서 단일이 아닌 전체 계류시스템의 장력을 줄일 수 있는 SP를 선정하기 위하여 국소장력은 식 (11)에 따라 각 계류선의 장력을 모두 합하여 산출하였다.
국소장력 계산에 적용된 국소격자의 면적은 계류시스템의 와치서클을 고려하여 선정하였다. 본 연구에서 대상으로 하는 현수삭(Catenary) 계류시스템의 와치서클은 일반적으로 수심의 10~15%이다. 150m의 수심에 따른 와치서클은 15~30m이므로 Fig. 1의 L로 명시된 국소격자의 한 변의 길이는 최대 와치서클의 지름인 60m로 선정하였다. 또한, 격자의 간격은 1m로 설정하였다. 즉, 현재 선박을 중심으로 60×60m2에 해당하는 면적에 1m의 간격을 가진 격자를 생성하므로 총 3,721개의 위치에서 국소장력이 계산된다.
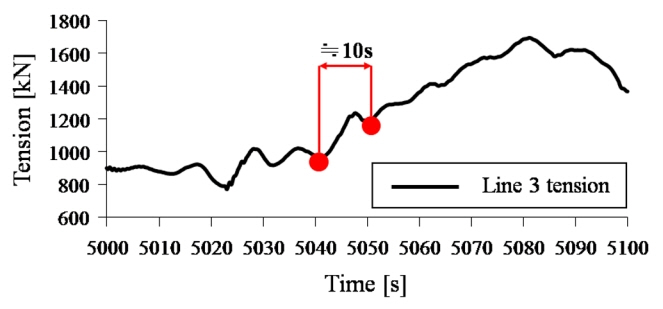
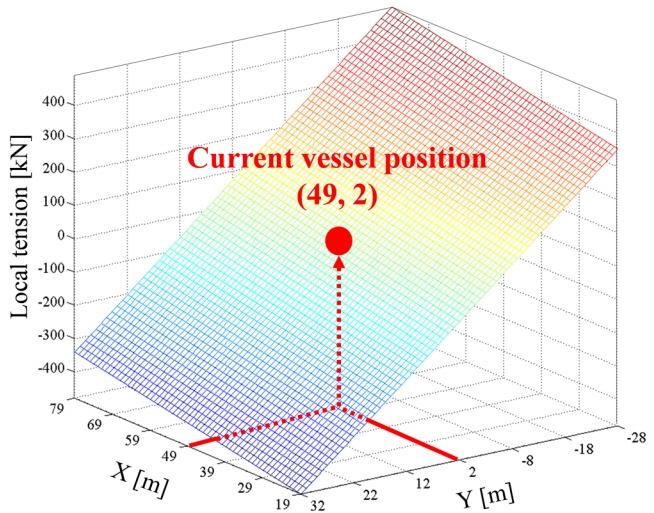
3시간의 해석을 통해 구조물의 전후동요(Surge), 좌우동요(Sway) 방향 위치 및 16개 계류선의 3시간 장력 이력을 산출하였다. 장력 시계열은 저역통과필터처리를 수행하였으며 최종적으로 국소장력 계산 과정에 사용된 데이터는 i=9120초, i-1=9110초에서 추출하였다. 10초의 시간증분은 Fig. 2와 같이 3시간 계류해석의 결과 산출된 장력 시계열에서 증감 추이를 유지할 수 있는 구간을 고려하여 선정하였다. Fig. 2는 3번 계류선의 3시간 장력 시계열에서 5,000~5,100초의 결과를 나타낸 그래프이다. 10초 이상의 시간 증분을 선택할 경우 장력의 미소한 증감 추이가 고려되지 않아 실제 장력 증감추이와 크게 벗어난 로컬장력이 산출될 수 있다. 따라서 본 연구에서 사용된 시간증분은 로컬장력계산 소요시간과 합리적인 결과 도출을 위하여 10초로 선정되었다. 9110초, 9120초의 위치 및 장력은 Table 3에 명시하였다. 이 데이터를 이용하여 식 (7)에서 식 (11)을 따라 900개의 국소격자 각 위치마다 국소장력을 계산하였다. 계산된 국소장력을 Fig. 3의 축에 나타내어 3차원 그래프로 도식화하였다. 그래프에 표시된 점은 9120초의 구조물 위치인 (49, 2)를 나타내며 이를 중심으로 계산된 장력의 상승 및 하강 방향을 추측할 수 있다. 예를 들어, 국소장력이 (79, -28)에 가까워질수록 높아지고 있으므로 SP는 (19, 32)에 가까운 위치로 선정되어야함을 알 수 있다. 따라서 국소장력은 실시간으로 가동되는 DP보조계류시스템의 SP 선정이 필요할 때, 최근의 장력과 위치 변화 추이를 고려하여 제어의 방향성 판단에 활용될 수 있다.
장력 추측을 위한 요소 중 전역장력은 동적 요소가 포함된 시뮬레이션을 수행하기 전에 정적해석을 통해 계산되는 장력이다. 전역장력은 Fig. 4과 같이 전역격자의 각 위치에서 구조물과 계류시스템의 정적해석을 통해 산출된다. 전역장력은 구조물의 위치변화에 따른 계류시스템의 부하분포를 직관적으로 나타내며 과도한 장력이 발생할 위치와 방향성을 SP 선정 과정에 포함시키기 위해 사용된 요소이다.
SP를 선정하기 위한 장력추측 과정에서 전역장력을 산출하기 위해 Fig. 4의 방식으로 시뮬레이션을 수행하였다. 대상 구조물 및 계류시스템은 2.4절의 국소장력의 시뮬레이션에 사용된 제원와 동일하다. 전역격자의 크기는 국소격자와 동일하게 계류시스템의 와치서클을 고려하여 60×60m2에 해당하는 면적과 1m의 격자 간격을 가지도록 정의하였다. 정적해석은 선박과 계류시스템의 시간영역 해석 프로그램인 Orcaflex를 이용하여 진행되었다.
산출된 장력을 Fig. 5와 같이 격자의 각 위치에 대해 수직축에 나타내면 도식화된 3차원 그래프를 생성할 수 있다. 전역장력은 구조물의 이동 시 과도한 장력의 발생구간을 직관적으로 나타내고 있으며 제어방향에 따른 계류시스템의 장력 변화 특성을 SP 생성 알고리즘에 포함시킬 수 있다.
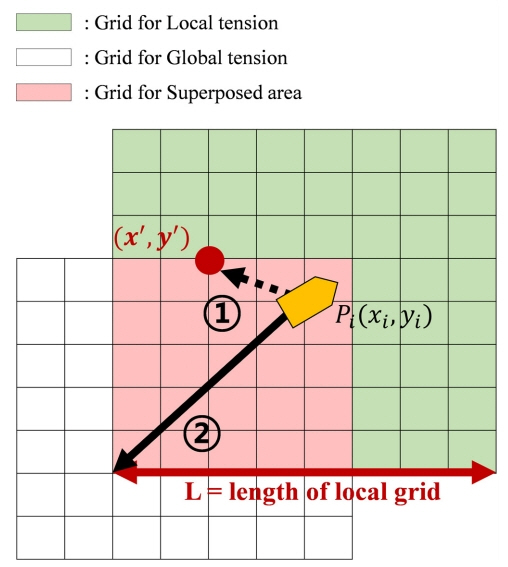
장력의 감소를 만족하는 SP는 Fig. 6의 빗금으로 표시된 구역과 같이 국소와 전역장력이 중첩된 구역에서 선정된다. 국소장력과 전역장력을 모두 고려한 영역에서 SP를 선정하기 위해 중첩하는 과정이 이루어지며 중첩된 구역의 각 격자 위치에서 국소와 전역장력이 합산된다.
국소와 전역장력의 합산은 식 (13)과 같이 α계수를 사용하였다. α는 Fig. 6과 같이 현재 구조물의 위치인 Pi 로부터 멀어질수록 값이 상승하게 된다. 즉, α는 장력중첩 과정에서 Pi 로부터 멀어질수록 전역장력의 영향을 크게 반영하기 위한 목적으로 사용된다. 이러한 과정은 중첩된 영역 내에서 현재 구조물의 위치로부터 멀어질수록 계류선의 형상변화 및 환경하중의 동적요소 영향이 커지기 때문에, 계류시스템을 선형으로 가정하여 장력을 추측한 국소장력보다 전역장력의 영향을 더 많이 고려하기 위함이다. 따라서 중첩된 영역의 각 노드(Node)들은 모두 다른 α값을 가지게 되고, 이 값은 식 (14)를 통해 이루어질 수 있다. 식 (14)의 분자는 현재 구조물의 위치로부터 떨어진 거리를 나타내고, 분모는 현재 구조물의 위치로부터 떨어진 최대 거리를 나타내며, 이는 Fig. 6에서 각각 ①과 ②로 표현되어 있다. 최종적으로, 장력의 감소를 만족시킬 수 있는 SP는 합산된 장력추측영역에서 최소의 장력을 가지는 위치로 선정하였다.
제시한 SP 산출과정의 알고리즘이 적용된 DP보조계류시스템을 이용하여 실시간으로 계산되는 SP의 장력 감소 만족도를 검증하기 위하여 시뮬레이션을 수행하였다. 구조물과 DP보조계류시스템이 3시간의 지속적인 환경하중에 노출되는 동안 구조물의 위치와 계류선의 장력이 경계조건을 초과하였을 경우, 본 연구에서 제안한 SP 산출 알고리즘으로부터 SP가 계산된다. DP시스템이 계산된 SP로 제어를 수행했을 경우 계류시스템의 장력 감소를 정량적으로 평가하였다.
시뮬레이션에 사용된 구조물과 계류시스템의 제원은 각각 Table 1과 Table 2에 소개하였고, DP보조계류시스템의 추진기는 Table 4에 명시하였다. 3개의 아지무스(Azimuth) 추진기와 2개의 터널 추진기(Tunnel thrusters)를 배치하였으며 PD제어기를 적용한 제어를 수행하였다. 제어대상인 운동모드는 전후동요(Surge)와 좌우동요(Sway)이며, 선수동요(Yaw)의 경우 터렛 계류시스템의 웨더베이닝(Weather-vaning)현상에 의해 자연적으로 변화하도록 허락되었다. PD제어기에 사용된 게인(Gain)은 계류시스템의 Surge 방향 자유감쇠시험(Free decay test)으로부터 산출된 계류시스템의 고유주기로부터 계산되었다. 본 연구에서 사용된 계류시스템의 Surge 방향 고유주기는 90초이며 P게인은 고유주기, 구조물의 질량과 부가질량을 적용하여 계산하였다. D게인은 계류시스템의 임계감쇠계수의 50%를 사용하였으며 얻어진 모든 게인값들은 Table 5에 정리하였다.
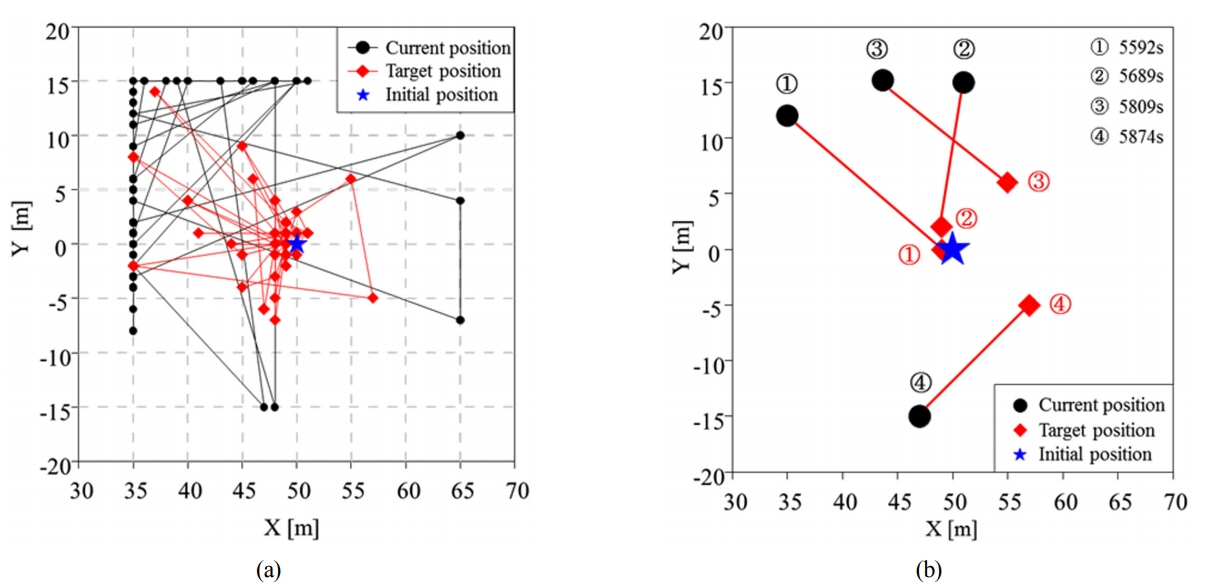
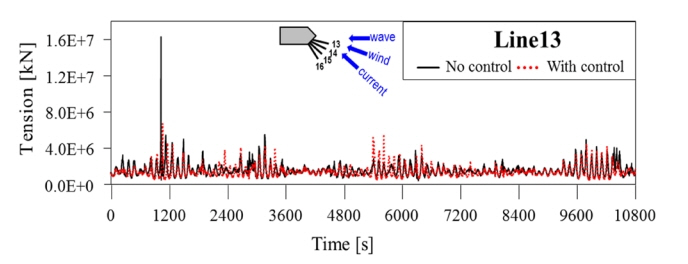
3시간의 시간영역 시뮬레이션이 진행되는 동안 구조물이 초기위치로부터 계류시스템 와치서클의 50%인 15m를 초과하거나 계류선의 MBL(Minimum breaking load)의 50%인 10,500kN을 초과하면 SP가 생성되면서 DP 제어가 시작된다. 장력 조건의 경우 계류시스템의 동적 거동에 의해 발생될 수 있는 과도한 장력을 방지하기 위한 조건이다. 해양 구조물이 제시된 조건을 만족하지 못했을 때, 연료효율적인 운영을 위하여 DP시스템은 작동하지 않도록 설정하였다. 3시간의 시뮬레이션 동안 구조물은 71번 제어시작 조건을 만족하였고, 이에 따라 71개의 SP가 계산되었다. Fig. 7(a)는 3시간 동안 계산된 SP의 위치와 동일한 시간에서의 구조물의 위치를 나타낸다. 계산된 SP값은 대부분 구조물의 초기 위치인 (50, 0)에 가깝게 설정이 되고 있다. Fig. 7(b)는 3시간의 시뮬레이션 중 5,592초에서 5,874초 사이에서 선택된 4개 위치에서의 결과를 나타내고 있다. 결과 그래프에 나타낸 초기 위치는 계류시스템의 장력이 가장 안정적인 위치를 나타낸다. 따라서 SP가 장력의 감소 방향으로 설정되고 있음을 알 수 있다. 본 연구에서 제시한 SP가 구조물의 초기위치 방향으로 계산이 되지만 항상 초기 위치인 (50, 0)으로 설정이 되지 않는 것은 DP시스템의 불필요한 가동을 최소화하기 위함이다. 만약 SP선정 알고리즘이 없다면, 구조물에 치명적인 영향을 끼치지 않는 온난한 환경조건에서도 SP가 항상 구조물의 초기위치로 설정이 되어 연료소비율 측면에서 비합리적인 제어전략이 될 것이다. 따라서 Fig. 7의 결과로부터 본 연구에서 제시한 SP 선정 전략은 장력과 위치변화 추이를 고려하여 연료소비율 측면에서 효율적인 SP를 산출하고 있음을 알 수 있다.
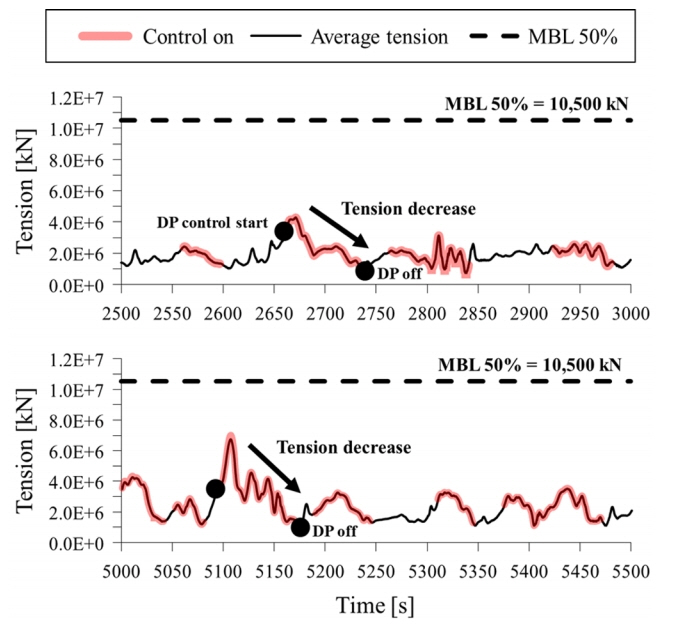
Fig. 8과 Fig. 9는 장력감소 SP 알고리즘이 적용된 DP의 제어 유무에 따른 계류시스템 장력을 기록한 그래프이다. Fig. 8은 환경하중이 가장 크게 작용하는 13, 14, 15, 16번의 계류선 중 13번 그리고 Fig. 9는 15번의 계류선에 대한 장력을 나타낸다. 두 결과로부터 SP로의 제어가 있는 경우에 최대 장력은 제어가 없는 경우에 비해 전반적으로 줄어들었음을 알 수 있다. 특히 1,100초경 발생된 과도한 장력은 제어로 인하여 최대 장력이 약 37%로 줄어들어 개발된 SP 알고리즘의 유효성을 관찰할 수 있다.
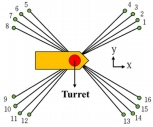
Fig. 10은 3시간의 시뮬레이션으로부터 산출된 각 계류선의 장력 중, 장력이 첫 번째와 두 번째로 크게 작용하는 계류선의 평균을 매 시간증분마다 계산하여 나타낸 결과 그래프이다. 따라서 매 시간증분마다 장력이 첫 번째와 두 번째로 크게 작용하는 계류선은 변동될 수 있다. 굵게 덧칠된 구간은 FPSO의 거동 및 장력의 변화가 알고리즘 작동조건에 해당하여 SP가 계산되고 DP의 제어가 가동되는 구간이다. 10,800초의 결과 중 2,500~3,000초와 5,000~5,500초의 결과를 나타냈으며 해당 시간에서의 DP 작동 조건은 위치변화에 의한 조건이다. SP제어가 작동하는 대부분의 구간에서 장력이 감소하는 것을 볼 수 있다. 이는 계산된 SP가 계류시스템의 장력부하 감소를 성공적으로 수행하고 있음을 나타낸다.
본 연구에서는 부유식 해양구조물의 과도한 표류와 장력 상승을 방지하기 위한 DP보조계류시스템의 SP 선정 전략을 제시하였다. SP는 장력의 감소를 만족하는 위치로 선정되어야 하며 이러한 SP 선정을 위하여 장력 추측이라는 전략을 제시하였다. 장력을 추측하기 위하여 구조물의 위치와 장력 변화추이를 고려한 국소장력과 계류시스템의 정적해석을 통해 산출된 전역장력을 함께 이용하는 방법을 소개하였다. DP보조계류시스템을 적용한 부유식 구조물에 대해 3시간 해석을 수행하여 제시된 SP 선정법의 실현 가능성과 성능을 판단하였다. 시뮬레이션 결과로부터, 선정된 SP로 구조물을 제어하는 동안 최대 장력이 감소하는 것을 알 수 있었다. 따라서 제안된 SP 선정 전략은 과도한 장력이 작용하는 것을 방지하고, 지속적으로 구조물이 위치경계조건 내에 위치하도록 DP보조계류시스템의 제어가 가능함을 확인하였다.
후기
본 연구는 산업통상자원부 산업기술혁신사업(과제번호: 10063 405) ‘위치유치와 계류시스템을 적용하여 ARC7 조건에서 연중 운용이 가능한 북극해 기반 부유식 해양구조물 형상개발’ 과제의 지원으로 수행되었음을 밝힙니다.
Table 1
Main dimension of model structure for simulation
| Description | Magnitude | Unit |
|---|---|---|
| Lpp | 244 | [m] |
| Breadth | 50 | [m] |
| Draft | 18.6 | [m] |
| Displacement | 163215 | [m3] |
| VCG | 18.5 | [m] |
Table 2
Configuration of mooring system
| Details | Configuration | |
|---|---|---|
| Type of line | Catenary |
|
| Composition | Chain-wire-chain | |
| Foot print size | 4*(Water depth) | |
Table 3
Local tension simulation at 9110 s and 9120 s
References
Barth Berntsen, PI., Aamo, OM., & Leira, BJ. (2008). Thruster Assisted Position Mooring Based on Structural Reliability. International Journal of Control, 81(9), 1408-1416. https://doi.org/10.1080/00207170701813844

Nguyen, DT., & Sørensen, AJ. (2009a). Setpoint Chasing for Thruster-assisted Position Mooring. IEEE Journal of Oceanic Engineering, 34(4), 548-558. https://doi.org/10.1109/JOE.2009.2034553


Nguyen, DT., & Sørensen, AJ. (2009b). Switching Control for Thruster-assisted Position Mooring. Control Engineering Practice, 17(9), 985-994. https://doi.org/10.1016/j.conengprac.2009.03.001

Ryu, S., & Kim, MH. (2003). Coupled Dynamic Analysis of Thruster-assisted Turret-moored FPSO. Proceedings of OCEANS 2003, IEEE, 3, 1613-1620. https://doi.org/10.1109/OCEANS.2003.178114

- TOOLS