|
 |
- Search
| J. Ocean Eng. Technol. > Volume 33(2); 2019 > Article |
|
Abstract
This study focused on the roll motion characteristics of a two-dimensional (2D) rectangular floating structure under regular beam sea conditions. An experiment was conducted in a 2D wave tank for a roll free decay test in calm water and the roll motion in a range of regular waves with and without heave motion to investigate the motion response and heave influence on the roll motion. A numerical study was carried out using Reynolds-averaged Navier Stokes (RANS)-based CFD simulations. A grid convergence test was conducted to accurately capture the wave condition on the free surface based on the overset mesh and wave forcing method. It was found in the roll free decay test that the numerical results agreed well with the experimental results for the natural roll period and roll damping coefficient. It was also observed that the heave motion had an impact on the roll motion, and the responses of the heave and roll motion from the CFD simulations were in reasonable agreement with those from the experiment.
선박과 해상 부유식 구조물의 과도한 횡동요는 선원과 승객의 승선감, 구조 신뢰성을 손상시키며, 궁극적으로 안정성을 위협하게 된다. 국제해사기구(International Maritime Organization, IMO)에 따르면, 최근 포스트-파나막스 컨테이너선(Post-panamax containership)의 경우 35도 이상의 극단적인 횡동요 운동을 경험하였으며, 구조 손상과 함께 약 400개의 컨테이너를 유실하는 사고가 있었다(IMO, 2002). 또한 FPSO(Floating production storage and offloading)와 Drillship과 같은 고부가가치 선박의 경우 보통한 곳에 고정되어 장기간 시추나 원유를 저장 등의 목적으로 운용되는데, 이러한 부유식 선박 구조물의 효율적이고 안전한 운용을 위한 설계에 있어 파랑 중 운동성능의 정확한 해석이 요구된다.
해상환경의 하중에 의한 선박의 6자유도 운동 중 횡동요 운동은 점성 감쇄영향으로 인하여 강한 비선형 특성을 가진다. 따라서 복잡한 점성효과와 유체동역학적 특성과 함께, 부유식 구조물의 운동해석에 대한 경험적, 실험적, 수치적인 연구가 활발히 진행되어지고 있다. Ikeda et al.(1977)는 이론 및 실험적 방법을 사용하여 횡동요 추정과 함께 2차원 물체의 횡동요의 와류감쇄(Eddy making damping)항이 주파수의 제곱에 비례함을 제시하였다. Chakrabarti(2001)는 횡동요 감쇄현상을 선체표면의 마찰감쇄(Skin friction damping), 와류감쇄(Eddy making damping), 조파감쇄(Wave damping), 부가물 부착으로 인한 감쇄(Bilge keel damping)로 구분하였다.
포텐셜 유동해석의 경우 유체를 비점성과 비회전성으로 가정하기 때문에 상, 하, 종 동요 운동들을 잘 추정하지만, 점성영향과 비선형특성을 가지는 횡동요 운동을 정확하게 추정하기에는 많은 어려움이 있다. Salvesen et al.(1970)은 실험을 통해 포텐셜 해석이 횡파(Beam sea) 중 사각형 구조물의 횡동요 크기를 과도하게 추정함을 보였다. Downie(1987)는 유동박리(Flow separation)와 와류(Vortex) 강도에 의한 점성효과를 고려한 경험치(Empirical factors)를 도입하여 횡동요 감쇄계수를 추정하였다.
유동측정에 대한 실험기법의 급속한 발달로 PIV(Particle image velocimetry) 기법을 이용하여 유동장 측정과 파도와 구조물 간섭에 의한 와류와 난류에 대한 연구에 가능하게 되었다. Dong et al.(1997)은 PIV방법을 사용하여 선수 주위의 유동흐름을 연구하였다. Yeung et al.(1996)은 자유수면에서 강제 횡동요를 하고 있는 평판에 의한 속도장을 측정하였으며, Jung et al.(2005)는 횡동요 운동과 상대운동에 의한 속도장을 측정하여 와류 및 난류의 특성을 파악하였다. Aloisio and Felice(2006)와 de Oliveira and Fernandes(2014)는 빌지킬(Bilge keel)주위의 유동장을 측정하여 선체와 와류의 간섭을 연구하였다.
최근 선박 및 해양구조물의 점성효과를 포함한 횡동요 추정 및 유동해석에 전산유체역학(Computational fluid dynamics, CFD)이 많이 적용되고 있다. Wilson et al.(2006)은 RANS(Reynolds averaged Navier-Stokes)기반 해석법을 이용하여 선박의 자유 횡동요 운동과 선체주위 유동을 계산하였으며, Chen et al.(2016)은 OpenFOAM(open-source CFD package)을 사용하여 2차원 사각형 바지선과 규칙파 간섭의 비선형성에 대해 연구하였다. Irkal et al.(2016)은 RANS 기법의 FLOW-3D를 사용하여 빌지킬 유무에 따른 횡동요 감쇄계수를 추정하여 모헝시험과 비교하였으며, PIV 방법을 이용하여 유동장을 계측하여 계산결과와의 상관관계를 연구하였다. 최근 전산수치해석에 대한 관심이 증가하고 있으나, 여전히 파랑 중 선박 및 해양 구조물의 운동 및 유동해석을 위한 CFD의 일반적인 접근법을 확립하기 위해서는 보다 많은 연구가 필요하다(Gokce and Kinaci, 2018).
본 연구에서는 부유식 사각형 구조물의 횡동요 운동의 정확한 추정과 횡동요와 상하운동의 연성을 파악하기 위해서 2차원 수조에서 2자유도(횡동요, 상하운동)를 허용하여 정수중 자유 횡동요 시험과 횡방향 규칙파(Regular beam sea condition)에서의 운동시험을 수행하였다. 또한 RANS 기법을 이용한 전산수치해석을 수행하였으며, 중첩격자(Overset mesh)와 유출면의 반사파 영향을 줄이기 위해 Wave forcing 방법을 사용하였다. 자유수면에서의 규칙파를 정확하게 재현하기 위해서 격자수와 계산시간 간격에 따른 수렴도 시험을 실시하여 계측 파고와 비교하였으며, 자유 횡동요 시험과 파랑 중 구조물의 운동에 대한 계산을 수행하여 횡동요 감쇄량과 운동 응답(Response amplitude operator, RAO) 및 시간영역에서의 횡동요와 상하운동의 수치해석 결과를 모형시험 결과와 비교하여 수치해석과의 상관관계를 조사하였다.
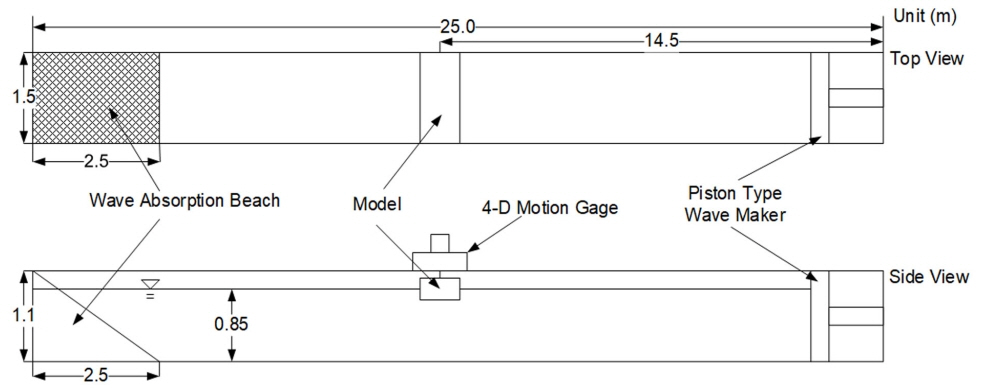
Fig. 1과 같이 모형시험은 2차원 수조에서 수행되었으며, 수조의 크기는 길이 25m, 폭 1m, 깊이 1.5m 이다. 수조 끝에서의 파도 반사를 최소화하기 위해서 길이 2.5m와 높이 1.1m 경사를 가진 소파망을 설치하였다. 조파기(Wave maker)는 Piston Type으로 컴퓨터로 작동되어지며, 다른 실험장비들과 동기화하였다.
아크릴로 제작된 사각형 단면의 구조물은 길이 0.99m, 폭 0.2m, 높이 0.015m로 파도는 오른쪽에서 왼쪽으로 진행하며 조파기로부터 14.5m 지점에 고정되었고, 정수면은 수조 바닥에서 0.85m로 유지하였다. 구조물의 무게중심(Centre of gravity, CG)은 구조물 바닥으로부터 0.06m이고, 흘수(Draft)는 0.07m로 횡동요의 회전중심은 정수면과 일치시켰다. 본 연구에서 횡동요의 정확한 추정을 위해서 구조물은 횡동요와 상하운동의 2자유도(횡동요, 상하운동)를 허용하여 횡방향 파도조건에 대해서 모형시험을 수행하였다.
정수 중에 사각형 단면 구조물의 자유 횡동요 시험(Free roll decay test)과 구조물과 파도의 상호 간섭에 의한 운동특성을 모형시험과 수치해석을 수행하여 비교 및 분석하였다. 자유 횡동요 시험을 통해 얻은 구조물의 횡동요 고유주기(Natural roll period, TN) 1.0s(ωN=6.283rad/s)를 포함하여 0.8~1.5s의 규칙파에 대해 실험하였다. 구조물의 운동특성에 대한 모형시험과 수치해석에 사용된 시험조건은 Table 1과 같다.
2차원 파랑중 해양구조물의 운동문제를 비압축성 난류유동(Turbulent flow)으로 가정하였다. 난류유동의 경우 연속 방정식과 운동량 보존 방정식인 RANS 방정식을 유동의 지배방정식으로 사용하였으며 식(1)-(2)와 같다.
여기서 ρ는 유체의 밀도, u ¯ i p ¯ u i ' u j ' ¯ τ ¯ i j
여기서 μ는 유체 점성계수이다.
파랑중 횡동요 시 구조물 주위의 복잡한 유동을 고려하여 난류모형으로 k-ω SST(Shear stress transport) 모형을 사용하였으며, 지배방정식의 해는 유한체적법(Finite volume method, FVM)으로 이산화 하였다. 자유수면을 고려하기 위해 유체의 밀도와 점성을 체적비율(Volume fraction)에 따라 이송방정식을 풀어 계산하는 VOF(Volume of fluid)기법을 사용하였으며, 시간과 공간에 대해 2차 정도의 수치 이산화 기법을 사용하였다. 본 논문에서는 이러한 수치해석 기법들을 이용하는 상용프로그램 STARCCM+(Siemense, 2018)를 이용하여 모든 수치해석을 수행하였다. 수치계산 조건은 모형시험과 같은 조건을 구현하기 위해 횡동요와 상하운동 구현이 가능한 DFBI(Dynamic fluid body interaction) 기법을 사용하였다.
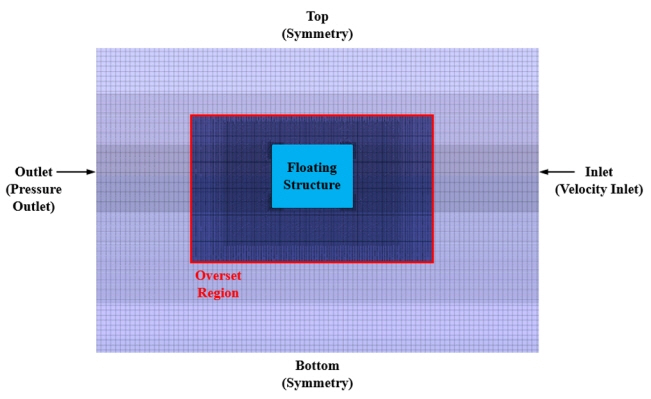
Fig. 2는 전산수치해석에서 사용한 2차원 사각형 구조물을 중심으로 계산 모델과 경계조건을 보여주고 있다. 유동장의 크기는 파가 입사되는 유입경계면은 상류쪽으로 6m에 위치해 있으며, 유출경계면은 하류 7m의 거리에 떨어져있다. 자유수면에서 깊이 방향으로는 0.85m, 높이 방향으로는 0.55m의 크기를 가진다. 본 계산에서는 운동이 큰 물체에 대한 효과적인 해석방법으로 구조체를 포함하는 내부격자와 전체 영역에 대한 외부격자를 중첩하여 사용하는 중첩격자 기법을 도입하여, 외부격자는 고정된 상태로 내부격자만 구조체 운동에 따라 격자의 변형없이 함께 운동하도록 하여 격자변화가 없도록 하였다(Field, 2013).
파랑중 선박 및 구조물의 수치해석에서 유출경계면에서의 반사파를 막아 반사파의 내부 유동장 영향을 최소화하는 방법은 중요한 요소이다. STAR-CCM+에서는 소파영역에 파감쇠계수(Wave damping coefficient)를 사용하여 파의 진폭을 감소시키는 방법(Peric and Abdel-Maksoud, 2016)과 유동장 내부의 파와 주어진 입사파를 일정 영역에서 선형파 이론(Linear wave theory)에서 얻어진 파 정보를 수학적으로 조화시켜 반사파를 강제하는 Wave forcing 방법(Enger et al., 2014)을 제공한다. Kim et al.(2018)은 격자수와 계산시간 간격 등의 수치조건에서 소파영역 내 파 감쇄감수를 사용하여 2차원 문제의 수치 민감도 분석하였으며, 추가적으로 Wave forcing 기법을 적용하여 3차원 파랑중 FPSO 운동 문제에 적용하여 타당성을 검토하였다. 본 연구에서는 계산 영역을 짧게하여 격자수를 줄일 수 있는 Wave forcing 방법을 사용하였으며, Forcing 영역은 유입경계면과 유출경계면에서 각각 파장의 1개(1.0λ)와 1.5개(1.5λ) 크기를 설정하여 계산하였다(Enger et al., 2014; Kim et al., 2018).
본격적인 수치계산에 앞서 주어진 조건의 규칙파를 정확히 시뮬레이션하기 위해 격자수와 계산시간 간격에 대한 수렴도 시험을 실시하였으며 시험 조건은 Table 2와 같다. 대표적으로 횡동요 고유주기에 해당하는 조건(Case no. C03, Wave period 1.0s, Wave length 1.56m)에 대해서 3가지(Coarse, Medium, Fine) 격자로 나누어 파의 10주기에 해당하는 10초간 계산하여 검토하였다. 격자는 ITTC(2011)에서 파랑중 선박의 전산유체 적용시 제안하는 파장(Wave length, λ)당 최소 80개의 격자수와, 파고(Wave height, H)에 대해서는 Kim and Lee(2011)이 제안하는 최소 20개의 격자수를 고려하여 수렴도 조건을 결정하였다. 전체 방정식들을 풀기위해 내부 반복계산 횟수(Inner iteration)를 10으로 하였고, 파의 주기에 대한 무차원 시간 간격(T/∆t)은 정도 높은 해석결과를 얻기 위해 CFL(Courant-Friedrichs-Lewy) 값이 0.25~0.30 되도록(Kim et al., 2018) 2
여기서 U는 파의 속도, ∆t는 시간간격, ∆x는 파의 진행방향에 대한 격자간격이다.
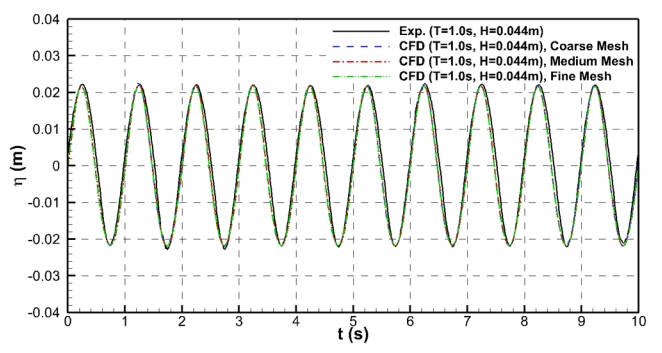
격자와 계산시간 간격에 따른 수치해석 수렴도를 파악하기 위해서 파랑중 운동 시험 전에 구조물이 없는 상태에서 구조물이 놓일 중심 위치에서 측정한 파고 측정결과와 계산결과를 Fig. 3에 비교하였다. 시간영역에서 실험에서 측정한 파고와 3가지 격자에 대한 수렴도 시험을 통해 계산된 파고는 모두 잘 일치하고 있는 것을 확인할 수 있었다. 격자에 따른 계산의 수렴도를 보다 자세하게 확인하기 위해서 Fine, Medium, Coarse 격자 사용 시 S1, S2, S3 파고를 조화해석(Harmonic analysis)을 통하여 각각 얻었으며, 수렴도(R)는 다음 식과 같다.
여기에서 ε21=S2-S1이며, ε32=S3-S2이다.
수렴도 해석결과 수렴도 R = 0.446로 단조수렴(Monotonic)하는 것을 확인할 수 있었다. 본 연구의 자유 횡동요시험과 파랑중 운동시험에서 사용할 Medium mesh의 경우 모형시험에서 계측한 파고보다 약 0.6% 크게 추정되었으며 파 주기는 약 0.2% 작게 추정되어, 수치해석 수행을 위한 만족할만한 수준으로 판단되었다.
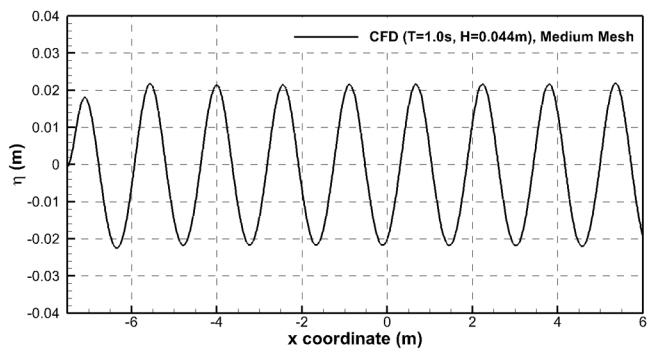
Fig. 4는 계산시간 10초에서 수치해석 전체 영역의 파고의 모습을 보여주고 있다. 파고 유입경계면과 구조물의 중심이 위치할 x = 0.0m의 위치에서는 시험조건(Wave height = 0.044m)과 유사한 파고를 나타내고 있었다. 유출경계면에서는 Wave forcing 기법의 적용으로 반사파는 없는 것으로 판단되었고, 파고가 다소 줄어드는 모습을 보였으나, 본 연구의 주 관심인 구조물 주위에서는 규칙파가 수치적으로 잘 재현되었다.
사각형 구조물의 파랑중 운동해석을 하기 전 정수중에서 초기 횡경사 각도까지 강제로 기울인 뒤 외력을 가하지 않고 자유롭게 운동하도록 하는 자유 횡동요 시험을 통하여 구조물의 동적특성을 파악하였다. 정수 중 횡동요 운동에 대한 운동방정식은 하기 식과 같이 표현될 수 있다.
여기에서 I'는 횡동요 질량 관성모멘트(I)와 횡동요 부가질량 관성모멘트(δI)의 합이며, ϕ는 횡동요 각, b는 횡동요 감쇠계수, c는 복원모멘트 계수이다.
Fig. 5는 22도의 초기 횡경사각에서 시간에 따른 모형시험과 계산결과의 횡동요량을 보여주고 있다. 참고로 자유 횡동요 시험의 수치해석 유입면과 유출면에는 압력유출(Pressure outlet) 경계조건을 사용하였다. 구조물의 횡동요 운동에 대한 고유주기(Natural roll period, TN)는 1.0s(고유진동수(Natural roll frequency, ωN)는 6.283rad/s로 모형시험과 수치계산이 일치된 결과를 보여주었다. 횡동요 운동은 넓은 사각단면 형상으로 감쇄가 급격하게 일어나고 있음을 알 수 있으며, 수치계산 결과가 모형시험 결과와 유사한 경향을 보이나 다소 크게 추정되는 것을 볼 수 있다. 이는 구조물이 없는 상태의 파랑중 수치해석 수렴도 시험과 다르게 구조물 표면의 마찰감쇄, 와류감쇄 등의 점성효과 차이에 기인한 것으로 판단되며, 향후 추가 연구를 통해 확인할 예정이다.
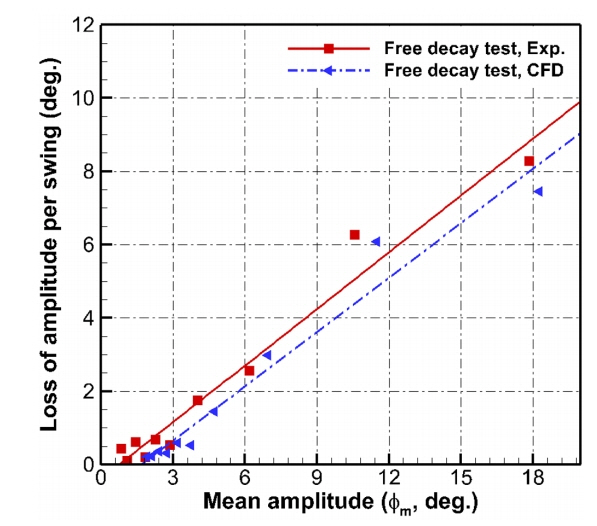
Fig. 6은 자유 횡동요 시험의 시간이력 결과를 이용하여 양의 횡경사각의 극값들(Positive peaks)과 음의 극값들(Negative peaks)를 사용하여 평균 횡동요량(Mean angle of roll, ϕm)에 대한 각 주기에서의 감쇄량을 보여주고 있다. 직선은 이산화된 결과에 대한 적합직선(Fitted line)으로 최소자승법(Least square)을 이용하여 나타내었다. 적합직선의 기울기를 이용하여 식 (6)의 횡동요 감쇄계수(b, Damping coefficient)를 Bhattacharyya(1978)가 제시한 방법에 따라 계산하였을 경우, 모형시험과 수치계산에서 얻은 횡동요 감쇄계수는 각각 0.160과 0.155로 유사한 결과를 얻을 수 있었다. 따라서 점성효과를 포함한 횡동요에 대한 감쇄계수를 본 연구에서 사용한 전산수치해석법을 통해 잘 추정할 수 있음을 알 수 있었다.
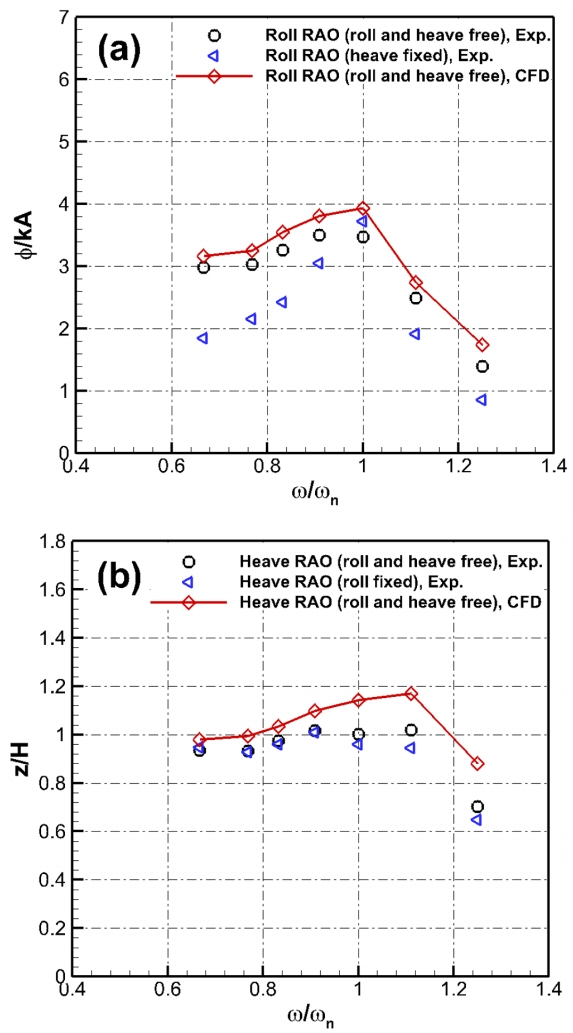
2차원 사각형 단면 구조물의 규칙파에서의 횡동요운동과 상하운동의 구속여부와 규칙파의 주기와 파고의 변화에 따른 각 운동의 특성을 조사하기 위한 모형시험을 수행하였다. 모형시험에서 상하운동 구속여부에 따른 횡동요 운동과 횡동요 운동 구속여부에 따른 상하운동의 응답, RAO 차이를 Fig. 7에서 보여주고 있다. Fig. 7(a)와 같이 고유주기에서 횡동요 운동은 상하운동 구속여부에 따라 차이가 적었지만, 낮은 주파수로 갈수록 상하운동을 구속하였을 경우 횡동요 운동의 응답이 작아지는 경향을 보여주며 높은 주파수에서도 응답이 작은 것으로 보인다. 따라서, 횡동요 운동의 정확한 추정을 위해서는 상하운동에 대한 연성을 고려해야 할 것으로 판단된다. Fig. 7(b)에서는 횡동요 구속여부에 따른 상하운동 응답차이를 보여주고 있으며, 모형시험에서 상하운동의 경우 횡동요의 구속여부에 따라 거의 차이가 없는 것으로 보인다.
수치해석의 횡동요 운동 응답의 경우 동일한 조건의 모형시험 결과와 매우 유사한 경향을 보였다. 그러나 자유 횡동요 시험과 유사하게 모형시험 결과보다 다소 크게 추정되었다. 또한 상하운동 응답의 경우 높은 파 주파수 영역에서 모형시험보다 계산결과가 크게 추정되었다. 이러한 차이는 수치계산의 수렴도 시험에서 구조물이 없는 파고의 경우 모형시험과 계산결과가 잘 일치하였으나, 자유 횡동요 시험과 같이 구조물이 있을 경우 계산결과가 모형시험보다 다소 크게 추정하는 것으로 판단되는데, 향후 이에 대한 추가적인 연구가 필요할 것으로 판단된다.
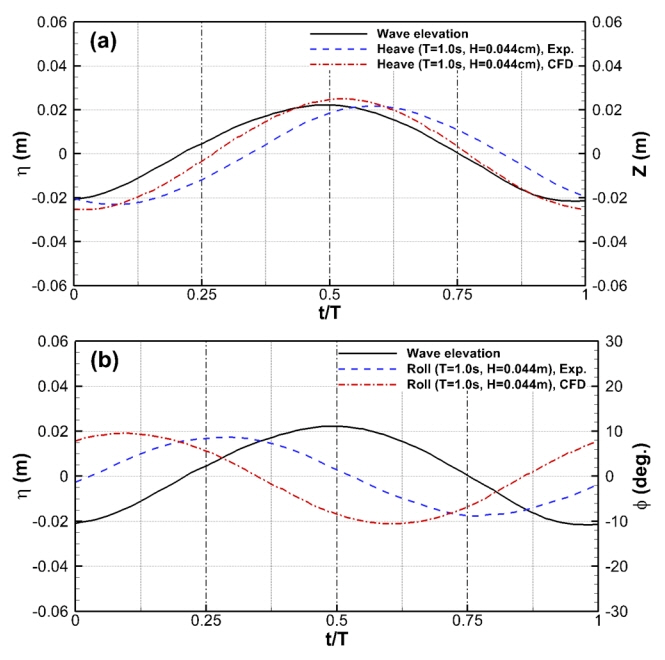
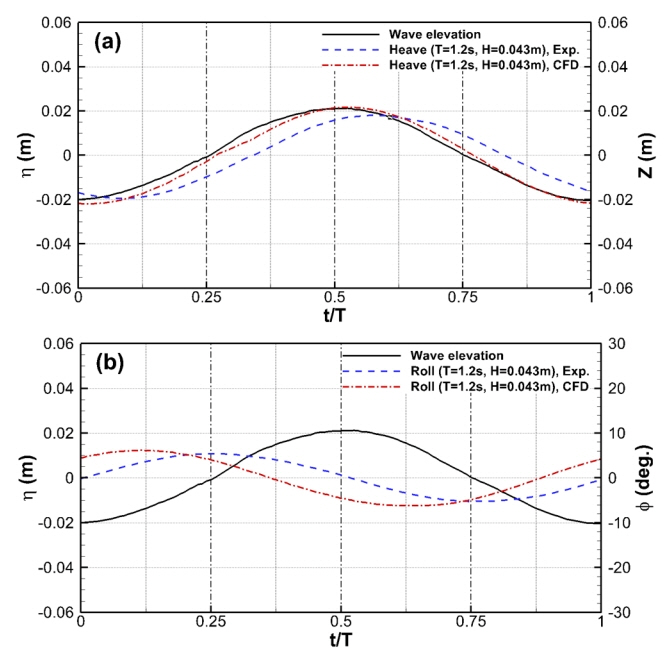
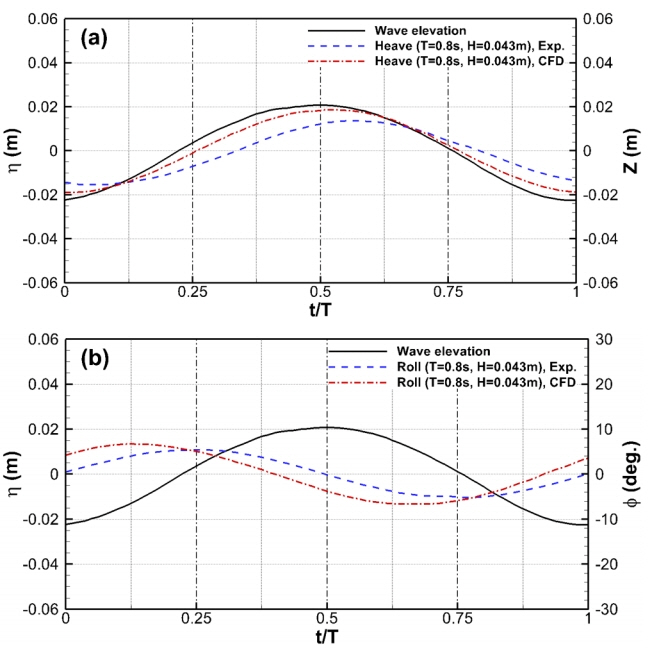
추가적으로 시간영역에서의 파의 주기로 무차원한 위상(t/T)에서의 구조물의 횡동요와 상하운동에 대한 모형시험과 수치해석 결과를 비교하였다. 모두 횡동요와 상하운동을 구속하지 않은 조건으로 횡동요 고유주기(T=TN = 1.0s, ω/ωn = 1.0)에서 횡동요와 상하운동의 위상차를 살펴보기 위해 입사파의 최대값이 t/T = 0.5에 위치하도록 하였다. Fig. 8은 시간영역에서 구조물 상하운동과 횡동요의 실험과 수치해석 결과를 비교하고 있으며, Fig. 7에서 보여주었듯이 수치해석 결과가 다소 크게 추정되었지만 서로 잘 일치하는 것을 볼 수 있다. 그러나 수치해석 결과는 Fig. 8(a)와 같이 상하운동에서는 약 0.05 주기(t/T) 정도 차이를, 횡동요 운동의 경우는 Fig. 8(b)와 같이 약 0.15 주기(t/T) 정도 차이를 보이고 있다. 다른 주기의 운동 결과와 비교했을 경우 횡동요 운동의 실험과 수치해석 결과 차이가 다소 크게 나는 것으로 보이는데, 이는 횡동요 고유주기에서는 큰 횡동요 운동으로 인한 상하운동의 연성과 구조물 근방의 유동차이가 다른 주기에 비해서 조금 더 크게 작용한 것으로 판단된다.
본 연구에서는 모형시험과 전산수치해석을 수행하여 횡방향 규칙파에서 2차원 사각형 부유식 구조물의 운동특성을 파악하였다. 모형시험은 2차원 수조에서 수행하였으며, 횡동요 운동의 정확한 추정과 횡동요와 상하운동의 연성을 파악하기 위하여 2자유도(횡동요, 상하운동)를 허용하였고, 횡동요 고유주기(TN=1.0s)를 포함한 일련의 규칙파 시험조건에서 시험하였다. 파랑 중 구조물의 운동특성에 대한 연구를 수행하기에 앞서 구조물 위치에서의 파고측정과 자유 횡동요 시험을 하였다. 전산수치해석은 비압축성 난류유동을 가정한 RANS 기법을 이용하였으며, 구조물의 큰 운동을 효과적으로 해석하고자 중첩격자를 사용하였고, 유출경계면의 반사파의 영향을 줄이기 위해 Wave forcing 방법을 사용하였다.
파랑 중 구조물 운동의 수치해석에 앞서 격자수와 계산시간 간격에 따른 수렴도 시험을 실시하여 수렴성을 확인하였다. 본 연구의 자유 횡동요와 파랑중 운동시험에 사용한 Medium mesh의 경우 시험에서 계측한 파고보다 0.6%로 크게 추정되어 만족할 만한 수준으로 재현됨을 확인할 수 있었다. 자유 횡동요 시험에서는 일치된 횡동요 고유주기를 모형시험과 수치해석에서 얻을 수 있었고 유사한 횡동요 운동량을 보였으나, 수치해석 결과가 다소 크게 예측함을 알 수 있었다. 평균 횡동요량에 대한 감쇄량을 비교하였을 경우 모형시험과 수치해석 결과가 잘 일치된 감쇄량을 보였으며, 따라서 점성효과를 포함한 감쇄계수를 수치해석을 이용하여 추정할 수 있음을 알 수 있었다.
횡방향 규칙파에서 구조물의 횡동요운동과 상하운동 구속여부 및 규칙파의 주기 및 파고의 변화에 따른 운동 특성을 조사하였다. 모형시험에서 횡동요 구속여부에 따른 상하운동의 응답은 거의 영향을 받지 않았으며, 상하운동을 구속하였을 경우에는 횡동요 고유주기를 제외한 조건에서는 횡동요 운동의 응답이 작아지는 경향을 보였다. 수치해석은 횡동요와 상하운동을 허용하여 계산하였으며, 같은 시험조건의 모형시험과 비교적 좋은 일치를 보여주었으나, 횡동요와 상하운동 모두 모형시험 결과보다 다소 크게 추정되었다. 추가적으로 3가지 주기(횡동요 고유주기, 긴 주기, 짧은 주기)에 대해서 시간영역에서 구조물의 횡동요와 상하운동의 모형시험과 수치해석결과를 비교하였다. 운동 응답 결과와 같이 유사한 결과를 보여주나 수치해석 결과가 다소 크게 추정되었으며, 상하운동에서는 약 0.05 주기 차이를, 횡동요의 경우는 약 0.15 주기 차이를 보였다. 이는 횡동요와 상하운동 연성에서 두 운동의 모형시험과 수치해석 차이에 따른 구조물 주위의 유동차이에 기인한 것으로 판단되며, 이에 대한 추가적인 연구가 필요한 것으로 판단된다.
또한, 비선형파와 불규칙파에 대한 수치해석 연구 및 모형시험 결과와 비교를 통한 검증과 구조물 주위의 점성효과에 따른 유동 및 압력에 대한 추가적인 연구를 진행 할 예정이다.
후기
본 연구는 조선해양플랜트글로벌핵심연구센터(GCRC-SOP, No. 2011-0030013) 및 산업통상자원부 산업기술혁신사업 ‘위치유지와 계류 시스템을 적용하여 ARC7 조건에서 연중운용이 가능한 북극해 기반 부유식 해양구조물 형상 개발’ (과제번호: 10063405) 과제의 지원으로 수행된 연구결과 중 일부임을 밝히며 연구비 지원에 감사드립니다.
Table 1
Test conditions for experiment and CFD
References
Aloisio, G., & Felice, F. (2006). PIV Analysis Around the Bilge Keel of a Ship Model in a Free Roll Decay. In XIV Congresso Nazionale AI VE. LA. Rome Italy. p 6-7.
Bhattacharyya, R. (1978). Dynamics of Marine Vehicles. Wiley: New York.
Chakrabarti, S. (2001). Empirical Calculation of Roll Damping of Ships and Barges. Ocean Engineering, 28(7), 915-932. https://doi.org/10.1016/S0029-8018(00)00036-6

Chen, L., Sun, L., Zang, J., Hillis, AJ., & Plummer, AR. (2016). Numerical Study of Roll Motion of a 2-D Floating Structure in Viscous Flow. Journal of Hydrodynamics, 28(4), 544-563. https://doi.org/10.1016/S1001-6058(16)60659-5


Dong, RR., Katz, J., & Huang, TT. (1997). On the Structure of Bow Waves on a Ship Model. Journal of Fluid Mechanics, 346, 77-115. https://doi.org/10.1017/S0022112097005946

Downie, MJ. (1987). The Discrete Vortex Method and the Calculation of Ship Motions. International Seminar on Engineering Applications of the Surface and Cloud Vorticity Methods, 2, 1-18.
Enger, S., Períc, M., & Monteiro, H. (2014). Coupling of 3D Numerical Solution Method Based on Navier-Stokes Equations with Solutions Based on Simpler Theories. Proceedings of XXXV Iberian Latin-American Congress on Computational Methods in Engineering, ABMEC Fortaleza, CE, Brazil.
Field, PL. (2013). Comparison of RANS and Potential Flow Force Computations for the ONR Tumblehome Hull for Min Vertical Plane Radiation and Diffraction Problems Masters Theses,. Virginia Polytechnic Institute and State University; Blacksburg, VA.
Gokce, MK., & Kinaci, OK. (2018). Numerical Simulations of Free Roll Decay of DTMB 5414. Ocean Engineering, 159, 539-551. https://doi.org/10.1016/j.oceaneng.2017.12.067

Ikeda, Y., Hemeno, Y., & Tanaka, N. (1977). On Eddy Making Damping Component of Roll Damping Force on Naked Hull. Journal of the Society of Naval Architects of Japan, 142, 54-64. https://doi.org/10.2534/jjasnaoe1968.1977.142_54

International Maritime Organization(IMO). (2002). Sub-committee on Stability and Load Lines and on Fishing Vessels(SLF), Review of the Intact Stability Code-Parametric rolling and its influence on container lashing systems. Submitted by the United States, SLF 45/6/7..
International Towing Tank Conference(ITTC). (2011). Practical Guidelines for Ship CFD Applications. Proceedings of the 26th ITTC.
Irkal, MAR., Nallayarasu, S., & Bhattacharyya, SK. (2016). CFD Approach to Roll Damping of Ship with Bilge Keel with Experimental Validation. Applied Ocean Research, 55, 1-17. https://doi.org/10.1016/j.apor.2015.11.008

Jung, KH., Chang, KA., & Huang, ET. (2005). Two-dimensional Flow Charcteristics of Wave Interactions with a Free-rolling Rectangular Structure. Ocean Engineering, 32(1), 1-20. https://doi.org/10.1016/j.oceaneng.2004.06.007

Kim, SP., & Lee, HH. (2011). Fully Nonlinear Seakeeping Analysis Based On CFD Simulations. Proceedings of the 21st International Offshore and Polar Engineering Conference Hawaii USA: 970-974.
Kim, JI., Park, IR., Suh, SB., Kang, YD., Hong, SY., & Nam, BW. (2018). Motion Simulation of FPSO in Waves through Numerical Sensitivity Analsysis. Journal of Ocean Engineering and Technology, 32(3), 166-176. https://doi.org/10.26748/KSOE.2018.6.32.3.166


de Oliveira, AC., & Fernandes, AC. (2014). The Nonlinear Roll Damping of a FPSO Hull. Journal of Offshore Mechanics and Arctic Engineering, 136(1), 011106. https://doi.org/10.1115/1.4025870


Perić, R., & Abdel-Maksoud, M. (2016). Reliable Damping of Freesurface Waves in Numerical Simulations. Journal of Ship Technology Research, 63(1), 1-13. https://doi.org/10.1080/09377255.2015.1119921

Salvesen, N., Tuck, EO., & Faltinsen, O. (1970). Ship Motions and Sea Loads. Transactions of The Society of Naval Architects and Marine Engineers, 78(8), 250-287.
Siemense. (2018). STAR-CCM+ 1104 User Guide. [Online] Available at: <https://support.industrysoftware.automation.siemens.com/general/documentation.shtml> [Accessed 01 Jan. 2018].
Wilson, RV., Carrica, PM., & Stern, P. (2006). Unsteady RANS Method for Ship Motions with Application to Roll for a Surface Combatant. Computers & Fluids, 35(5), 501-524. https://doi.org/10.1016/j.compfluid.2004.12.005

Yeung, RW., Cermelli, C., & Liao, SW. (1996). Vorticity Fields Due to Rolling Bodies in a Free Surface - Experiment and Theory. 21st Symposium on Naval Hydrodynacmics Trondheim Norway.
- TOOLS
-
METRICS

-
- 4 Crossref
- Scopus
- 5,093 View
- 143 Download
- Related articles in JOET
-
Numerical Analysis for Motion Response of Modular Floating Island in Waves2023 February;37(1)