|
 |
- Search
| J. Ocean Eng. Technol. > Volume 33(3); 2019 > Article |
|
Abstract
A submerged breakwater is one of the coastal structures used to reduce wave energy and coastal erosion. However, a submerged breakwater has a negative aspect in that a strong rip current occurring around an open inlet due to a difference in mean water levels at the front and rear sides of the structure leads to scouring. Such scouring has a bad effect on its stability. In order to eliminate this kind of demerit, this study investigated an artificial reef of the overflow type with openings. We also developed a program where the flows around the artificial reef of the overflow type could be analyzed numerically. An unstructured grid system was used to cover the various geometries, and the level set method was applied to treat the movement of the free surface. To verify these numerical schemes, hydraulic physical tests were performed on the submerged breakwater and double breaking type artificial reef. Then, the wave height and velocity distribution around the reef were examined using the experimental results. Comparisons between the results of hydraulic and numerical tests showed reasonable agreement.
최근 우리나라의 연안은 기후변화로 해수면의 상승에 의한 고파랑 등의 외력증가와 더불어 연안해역의 개발에 따른 해빈의 침식 및 세굴에 의한 해안선의 변형 등의 피해사례가 급증하고 있다. 해빈침식 및 표사이동은 단순한 침식 문제가 아니라 국토보존과 연안재해의 측면에서 인식되고 있다. 이 같은 문제를 해결하기 위해 입사파에너지를 감소시켜 표사의 이동을 최소화하여 해빈침식을 억제하기 위한 돌제, 헤드랜드, 이안제, 잠제(인공리프) 등을 설치하는 강성공법과 흐름을 부분적으로 차단하거나 손실된 모래를 보충하는 양빈, 해빈배수 등의 연성공법 등이 제안되고 있다. 또, 강성공법과 연성공법을 복합적으로 적용하는 잠제와 인공 양빈을 결합하는 형태의 적용이 이루어지고 있다.
잠제는 연안 경관을 유지하고 확보하는 효과와 함께 파랑저감을 통해 연안해역의 저질 이동을 방지하여 해빈의 현상유지 및 회복을 도모할 수 있는 것으로 알려져 있다. 그러나 잠제는 입사파에너지를 마루부에서 강제쇄파를 통해 저감시키기 위해 입사파장(L)의 0.5배 정도의 광폭 마루부가 필요하며, 그리고 감쇠된 파에너지는 해빈류를 발생하거나 잠제 배후부 수위를 상승시켜 침식대책에 부정적인 측면으로 작용하기도 한다(National Association of Sea Coast, 2004). 이 같은 현상은 해안선 부근의 전빈경사를 증가시키거나 잠제와 잠제사이의 개구부를 통한 이안류를 크게 하여 표사의 외해유출을 발생하는 것으로 알려져 있다.
그리고 잠제나 인공리프는 마루높이가 정수면 아래에 위치하기 때문에 인공리프 전면의 수심과 마루부와 급격한 수심의 변화에 의해 구조물 주위에서 복잡한 수리학적 변동을 초래하므로 이를 규명하기 위한 다양한 연구가 수행되어 왔다(Lee et al., 2013; Kakemizu and Kimura, 2005; Hur et al., 2017).
본 연구에서는 쇄파 시 인공리프 배후에서 발생하는 수위상승과 향안류를 최소화 할 수 있도록 Fig. 1과 같이 고안된 월류형 인공리프를 대상으로 파랑-인공리프의 상호작용에 따른 해안수리학적 특성을 검토하였다. 월류형 인공리프의 파랑감쇠원리는 입사파 에너지를 Fig. 1과 같은 전⋅후면 월류제체 상부 및 내부에서 쇄파 및 와류를 이용하여 소산하는 방식으로 기존 광폭잠제에 비해 마루폭을 축소한 것이다. 그리고 쇄파에 의해 발생하는 흐름을 외측으로 배제하기 위해 월류식 인공리프 전면부에 개구부를 설치하여 구조물 배후로 수송되는 파에너지 및 향안류와 배후 수위상승을 억제하도록 고안되었다.
이러한 인공리프 및 잠제주위 수면변동의 수치해석을 위해서 오픈소스 기반의 OLAFOAM(Higuera et al., 2015) 등을 이용한 수면변동 해석이 많이 사용되고 있으며, 특히 잠제 및 인공리프 주변의 파랑 및 흐름 특성에 관해서는 Hur and Lee(2007), Hur et al.(2010), Lee et al.(2017) 등은 VOF(Volume of fluid)기반의 수치모형을 통한 연구가 있으며 본 연구에서는 3차원 수면변동을 해석할 수 있는 프로그램을 자체 개발하여 적용하였다. 자유 표면 수치해석 방법으로는 VOF법(Lopez et al., 2005) 및 레벨셋방법(Peng et al., 1999)이 널리 사용되고 있는데 본 연구에서는 레벨셋 방법으로 자유표면의 변동을 해석하였다(Sussman et al., 1998). 일정 시간 단계마다 거리 함수를 재초기화 하는 방법으로 수치 확산을 감소시키는 레벨셋 방법에서는 자유표면상의 속도가 영역내에서 사용되어야 하므로 자유표면상의 속도를 영역 내로 전달하는 파동방정식 형태의 미분방정식을 추가적으로 처리해야 하는 문제가 발생한다(Peng et al., 1999). 본 연구에서는 영역 내의 격자 연결 정보를 이용하여 파동방정식 형태의 미분방정식을 처리하지 않는 방법을 제시하였다.
본 연구에서는 월류형 인공리프 주위의 파랑전달 및 흐름변동 등에 대한 해안수리학적 특성을 파악하기 위하여 레벨셋 방법에 의한 3차원 수면변동을 위한 수치해석(Shin et al., 2018)과 수리모형실험을 통해 검토하였다. 수리모형실험은 무차원파수(kh), 파형경사(H/L) 및 인공리프 개구부에 따른 수리 특성을 파악하기 위해 입사파 및 개구부 특성을 고려한 다양한 수리조건에 대해 수행하였으며, 비교 및 검토 결과 비교적 타당한 결과를 나타내고 있음을 확인할 수 있었고 본 연구에서 제안된 월류형 인공리프가 쇄파성능 및 파랑제어 측면에서 효과적임을 확인할 수 있었다.
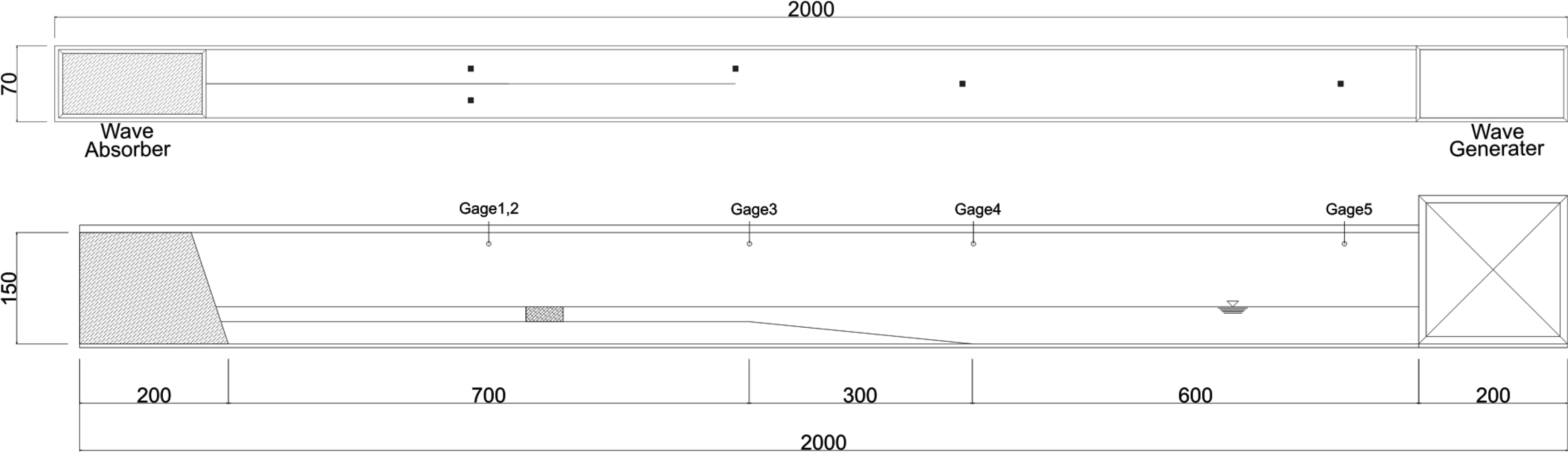
월류형 인공리프에 의한 파랑 및 흐름의 자유수면 변동 특성을 검토하기 위한 수리실험은 Fig. 2와 같은 길이 20.0m, 높이 1.25m, 폭 0.70m의 2차원 단면 조파수로에서 이루어 졌다. 조파수조는 피스톤형식 조파장치를 통해 규칙파, 불규칙파의 발생이 가능하며, 수조의 하류측 끝부분에는 반사파를 최소화하기 위해 경사투과제를 사용한 다공성 재질의 소파장치를 설치하였다. 수로바닥의 경사는 쇄파 발생위치, 파랑변형 및 인공리프 구조물에 작용하는 파랑특성과 직접 관련되므로 본 연구에서는 2차원수로에의 효과적인 실험파랑의 유도를 위해 조파판에서부터 6.0m 떨어진 곳에서부터 1/10의 바닥경사를 3.0m 설치하였다. 또 조파수로는 Fig. 2의 평면도에서 보듯이 2등분하여 한쪽 수로에는 모형 구조물을 설치하고 나머지 수로는 입사파를 통과시켜 수로내 반사파의 재입사가 발생하지 않도록 하거나 양측 수로에 모형 구조물을 설치하여 동시에 파랑 변동을 측정할 수 있도록 하였다.
Fig. 3(a)는 조파수로를 양분하여 월류형 인공리프와 TTP(Tetrapod)난적 잠제를 각각 설치하여 수리실험을 수행하는 것을 보이고 있다. 월류형 인공리프의 소파원리는 기존 광폭잠제와 유사하며, 마루부에서 강제쇄파를 통한 파고감쇠에 의해 배후 해빈역을 보호하기 위한 해안구조물이다. 인공리프는 Fig. 3(b)에서 보듯이 전면에 개구부가 있는 U자형의 블록형 구조물로서 입사파 에너지를 전⋅후면 월류벽에서 강제쇄파하고 구조물 내부의 중앙돌출부를 중심으로 쇄파된 와동을 전⋅후 유수실에서 분리하여 파에너지를 소산하는 방식이며, 입사파 내습하는 전면 월류벽에 개구부를 설치하여 쇄파에 의해 발생된 해빈류를 외해측으로 배출하여 향안류를 최소화하도록 고안한 것이다. Fig. 4에는 입사파고 H=7.5cm, 입사파주기 T=1.58s가 내습하는 경우 인공리프 내부에서 강제쇄파에 따른 시간경과(t=10.0s 및 10.15s)에 의한 와류 형성 및 이동 과정을 나타내었으며, 이에 따른 외해류의 흐름발생을 보이고 있다. 외해류 발생에 의해 월류제 배후로 수송되는 흐름에너지를 감쇠하는 효과를 가질 것으로 기대되므로 파고변동, 인공리프 내외부의 흐름 및 연직 월류벽에 작용하는 파압의 측정이 필요하며, 특히 파랑의 효율적인 저감을 위한 최적의 월류폭, 월류제 전면 개구부의 크기를 파악하기 위한 월류형 인공리프 주위의 수면변동 특성 파악이 요구된다.
이를 위해 파고는 용량식 및 초음파식 파고계를 동시에 사용하여 측정하였고, 월류형 인공리프 개구부 및 인공리프 내부 유속은 전자식유속계(Kenek VE10)를 사용하여 관측하였다.
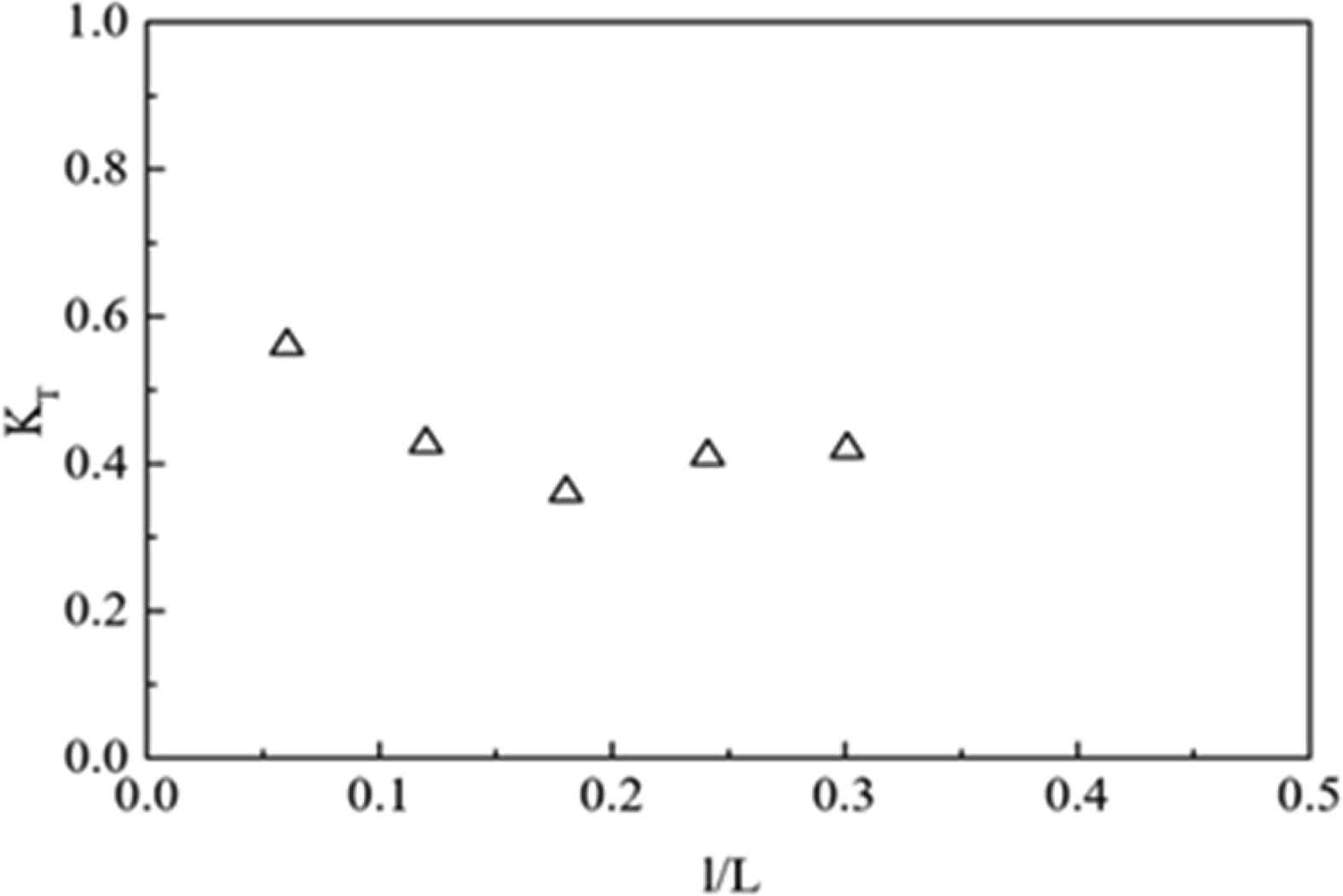
월류형 인공리프 최적의 마루폭에 대해서는 Fig. 5에 나타낸 바와 같이 콘형(Cone type)블록에 관한 파랑의 전달특성을 2차원 수치해석을 통해 Kakemizu and Kimura(2005)는 입사파 H=3.0m, T=11.0s 조건에 대해 입사파장에 대한 마루폭의 비(l/L)가 0.1~0.2인 경우 전달계수 KT가 최소가 됨을 제안하였으며, Hong et al.(2017)은 월류형 인공리프의 최적 마루폭을 산정하기 위하여 인공리프 마루폭 15m에 대해 파고 H=1.5m, 3.0m, 주기 T=6s, 8s, 10s 및 12.0s의 규칙파 조건에 대해 CFD 모형인 OpenFOAM을 통해 수치해석하여 l/L=0.19 인 경우 전달계수 KT가 최소로 나타나, 기존 광폭 잠제의 마루폭을 l/L=0.5을 고려하는 것에 비해 월류형 인공리프는 이의 1/2 정도의 마루폭으로 최적의 파고감쇠가 가능한 것으로 검토되었다.
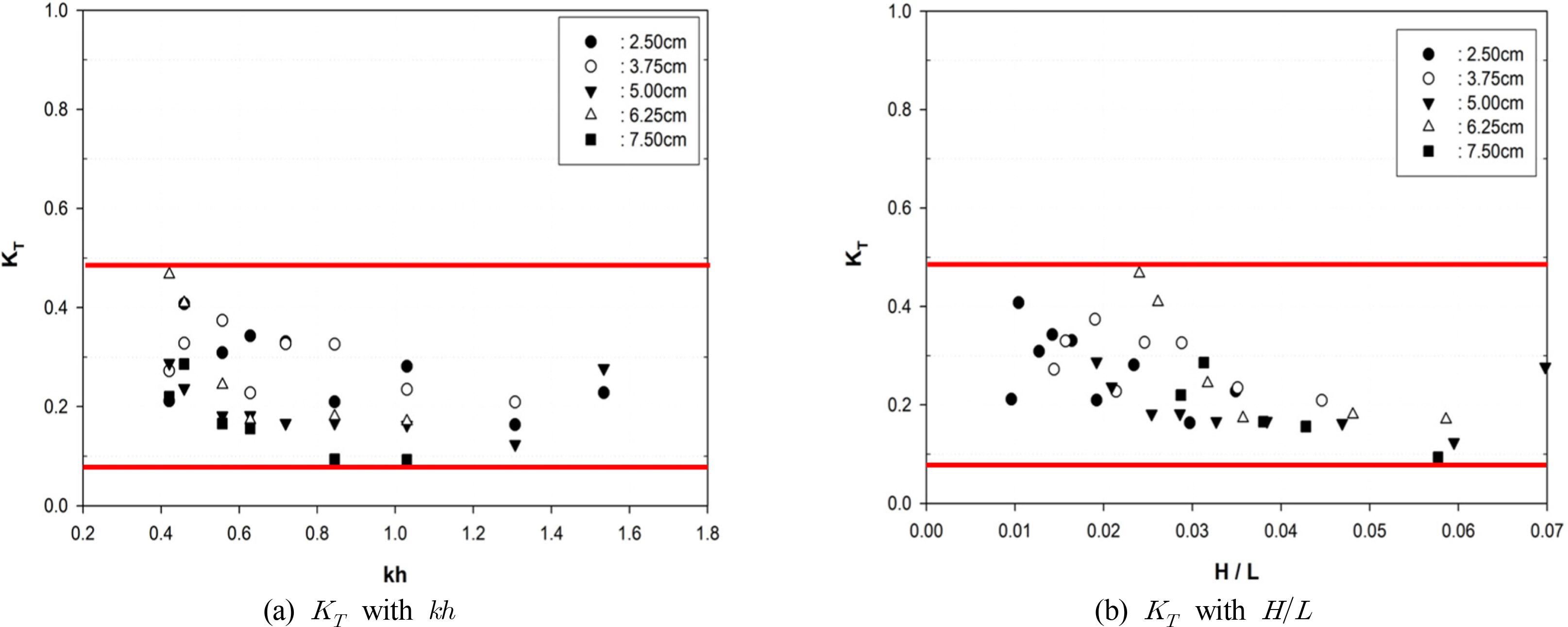
전면 월류벽의 개구율에 따른 월류형 인공리프와 광폭잠제에 의한 파랑의 전달특성을 비교 검토하기 위해 Fig. 3(a)에 나타낸 바와 같이 조파수로를 양분하여 월류형 인공리프와 광폭잠제를 설치하여 파고 전달특성에 대해 실험을 수행하였으며 그림에서 보듯이 월류형 인공리프는 수심 h=17.5cm에 놓여있으며, 마루폭 l=37.5cm, 광폭잠제는 마루폭 l=100cm로 하였다. 파랑 전달계수(KT)는 입사파고(HI)에 대한 전달파고(HT)의 비로 정의되며, 전달율 실험은 전면 월류벽의 개구율 0%, 30% 및 50%로 구분하여 실험하였으며 TTP난적의 광폭잠제와 동시에 수행하였다. 입사파고 HT는 2.5cm, 3.75cm, 5.0cm, 6.25cm 및 7.5cm 등 5개의 파고에 대해 0.79s, 1.26s, 1.58s 및 1.89s 4개의 주기별로 총 20개 그리고 인공리프 모형 3개안 및 광폭잠제 1개안 등 총 80개 실험안에 대해 전달계수를 측정하였다. 그리고 월류형 인공리프의 마루높이는 0.00, 광폭잠제는 (-)1.25cm로 하였다.
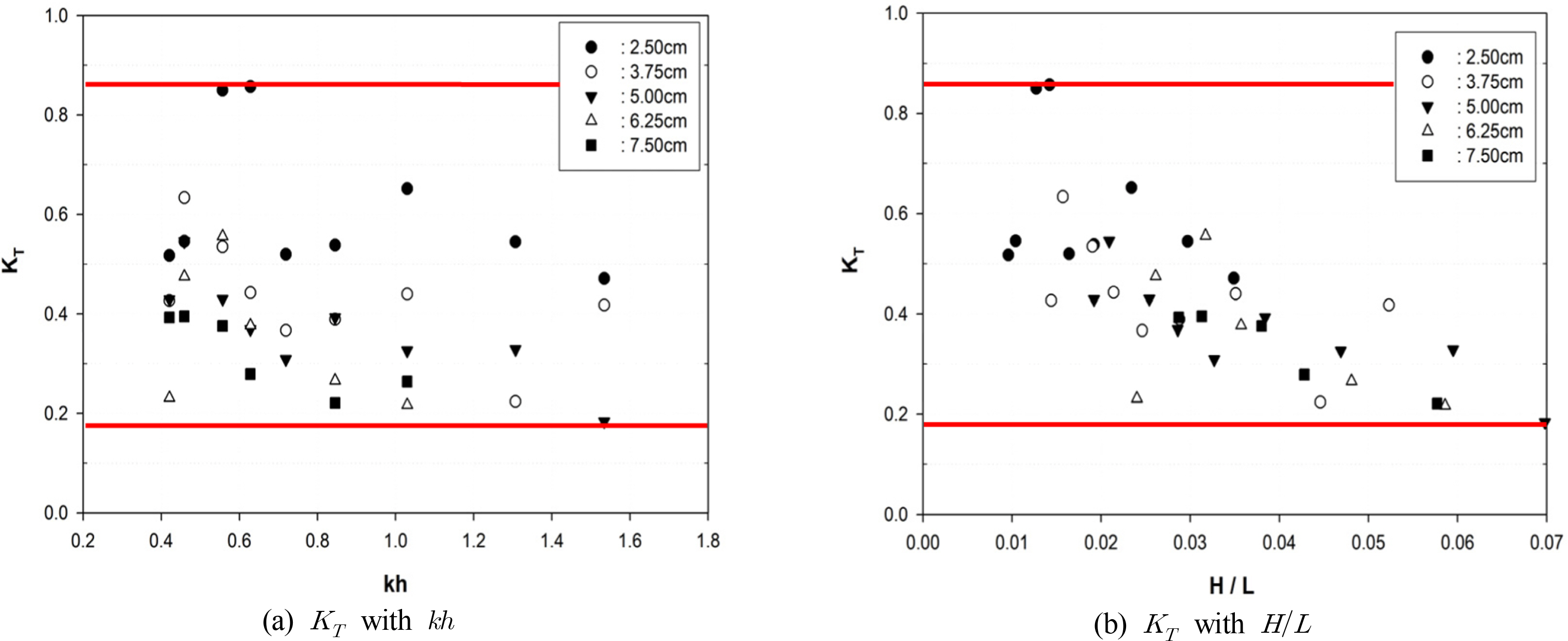
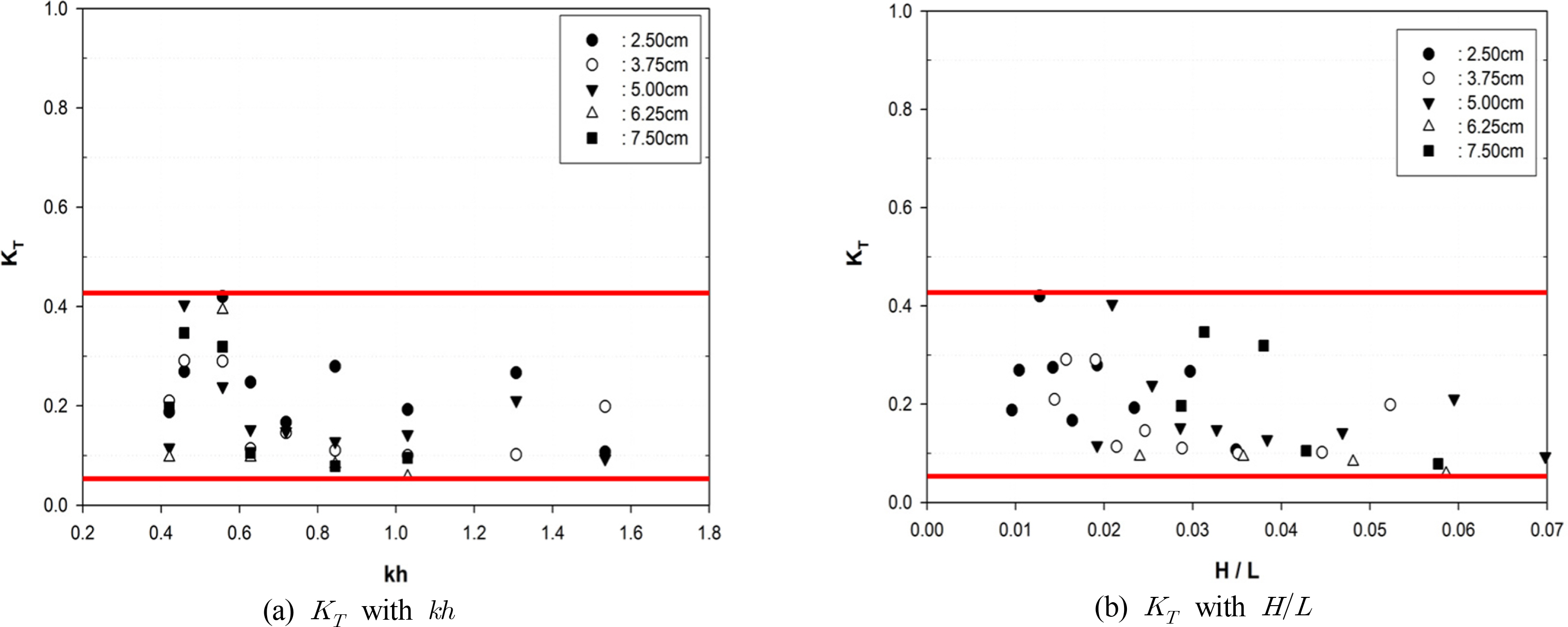
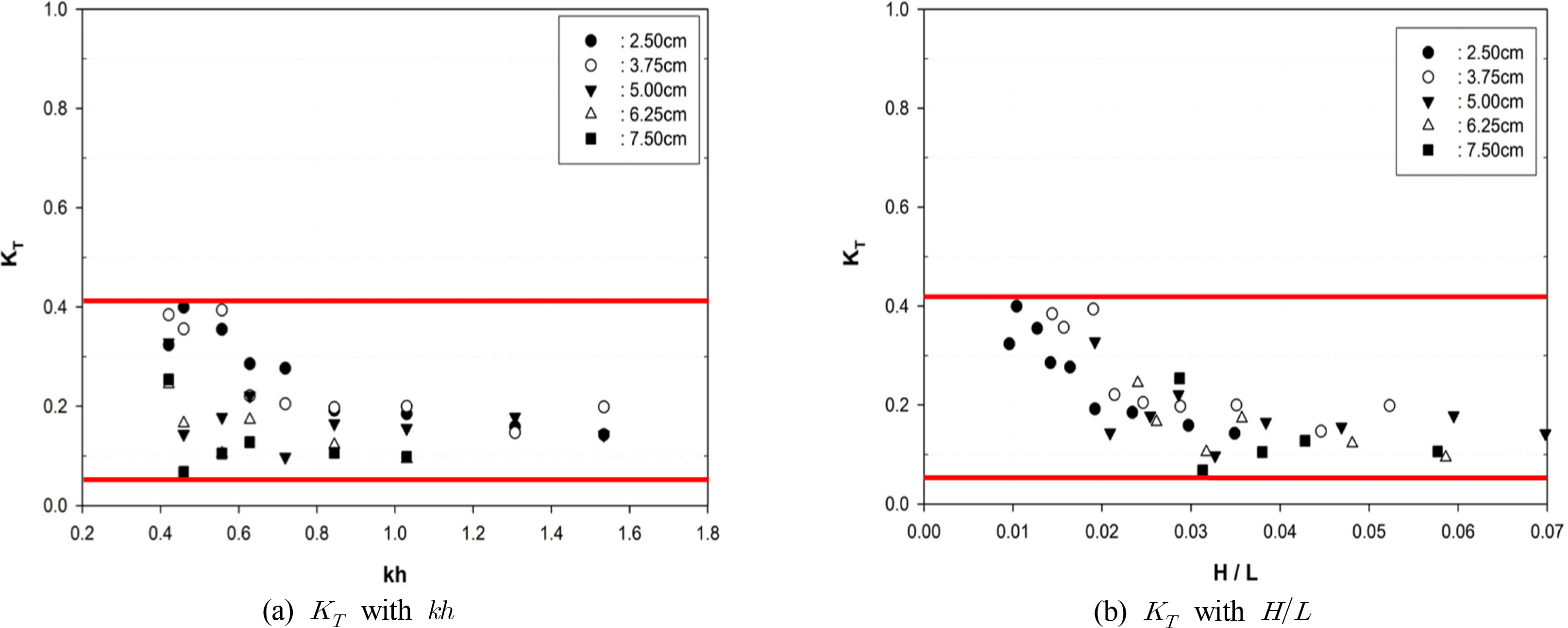
실험결과는 Figs. 6-9에 광폭잠제와 월류형 인공리프의 개구율에 대해 입사파고에 따른 파형경사(H/L)와 무차원파수(kh)의 함수로 전달계수(KT)의 관계를 각각 나타내었다. 입사파고와 입사파장의 비를 나타내는 파형경사(H/L)는 파의 선형성을 나타내는 무차원 값으로 실험결과에서 알 수 있듯이 파형경사가 작아짐에 따라 전달계수가 증가하며, 파형경사가 증가함에 따라 인공리프 전면수역 및 구조물에 의한 쇄파발생이 용이하여 전달계수는 비선형적으로 감소하는 특성을 보여주고 있다. 이는 입사파 주기에 영향을 크게 받고 있음을 알수 있다. 그리고 천해 특성을 나타내는 무차원파수(kh)에 대한 전달계수 KT 는 그림에서 보듯이 kh가 증가함에 따라 전달계수가 완만히 감소하고 있는 특성을 보이고 있다. 특히 입사파고가 증가할수록 무차원 파수에 따라 전달계수가 감소하고 있다. 광폭잠제와 개구율에 따른 월류형 인공리프와의 전달특성을 비교한 결과 광폭잠제인 경우 입사파고가 상대적으로 작은 HI=2.5cm인 경우 최대전달계수KT=0.85로 크게 관측되었으며, 무차원파수나 파형경사에 따른 변동 폭이 크게 나타나지만 평균적으로 KT=0.45~0.55의 범위를 나타내고 있다.
개구율의 변동에 따른 파랑전달특성은 인공리프인 경우 광폭잠제에 비해 크게 저감되는 것으로 관측되었으나, 월류형 인공리프인 경우는 최대 전달계수 KT=0.40을 거의 초과하지 않으며 평균적으로 KT=0.20~0.30 정도로 실험결과 나타났다. 50% 개구율의 인공리프인 경우 전면 월류벽의 개구부를 통과한 파랑의 부분적인 월파에 의해 전달계수 KT=0.40을 상회하는 경우도 나타나고 있다. 그러나 전체적으로 광폭잠제와 개구율에 따른 월류형 인공리프와의 전달특성을 비교한 결과 전달계수의 측면에서 약 40~50% 정도의 감소효과가 있는 것으로 관측되었다.
비압축성 유동을 가정하면 무차원화된 연속방정식 및 지배방정식은 다음과 같다(Sherman, 1990).
여기서, 속도 (u, v, w)는 특성속도 U로 (x, y, z)는 특성길이 L로 t는 L/U로 p는 ρU2으로 무차원화 되었고, R은 UL/v를 Fn은 U/(gL)1/2을 의미하며 v는 유체의 동점성계수 g는 중력가속도를 의미한다.
대류항, 소산항 및 중력항으로 구성된 F,G,H를 다음과 같이 정의하고,
식 (2)를 시간에 대하여 이산화하면 다음과 같으며 위첨자 n은 시간 단계를 의미한다.
식 (1)의 연속방정식을 적분하면 다음과 같으며 n → = ( n x , n y , n z )
식 (3) 및 식 (4)와 같이 시간 및 공간에서의 이산화 과정시 차분 방법은 FDM(Finite difference method) 방법을 사용하였으며 식 (6)에서와 같이 압력 방정식은 적분형 방정식을 사용하였다. 차분시 식 (3)의 소산항은 중심차분법을 대류항은 상류차분법을 이용하였다.
비정렬격자계에서의 이산화에 따른 차분방법은 각각의 격자 기반 국부좌표계(Local coordinate system)를 이용하여 처리하였다(Shin, 2012; Shin and Lee, 2014).
자유표면 형상에 따라 전체 격자는 자유표면을 포함하는 경계셀 격자를 기준으로 공기 영역과 유체 영역 격자로 구분할 수 있다. 본 연구에서는 단상류로 처리하여 유체 영역의 유동을 수치해석하였다. 경계셀 격자에 대기압 경계조건을 부여하였으며 경계셀 격자에 존재하는 자유표면 위치에서 대기압이 되도록 압력값을 외삽하였다. 구조물 및 수조 벽면에서 법선 속도는 0이며 접선방향으로는 슬립조건을 주어 자유표면의 움직임을 용이하게 하였고 압력조건은 식 (2)을 이용하여 벽면에서의 압력 미분값을 구하여 경계조건으로 사용하였다. 식 (1)의 연속방정식을 만족시키는 압력 포아손 방정식으로부터 압력을 구하게 되며 식 (2)로부터 다음 시간 단계의 속도를 구할 수 있다. 엇갈림격자(Staggered grid)를 사용하여 격자면(Cell face) 중심에서의 속도가 계산되는데 경계셀 및 공기영역에서의 속도는 인접한 유체 영역의 속도로부터 내삽 또는 외삽한 값을 사용하였다(Shin, 2017). 한편 시간 전진은 Runge-Kutta 2차 방법을 사용하였으며 자유표면 수치해석은 레벨셋 방법을 이용하여 수치해석하였다(Sussman et al, 1998; Shin et al, 2018).
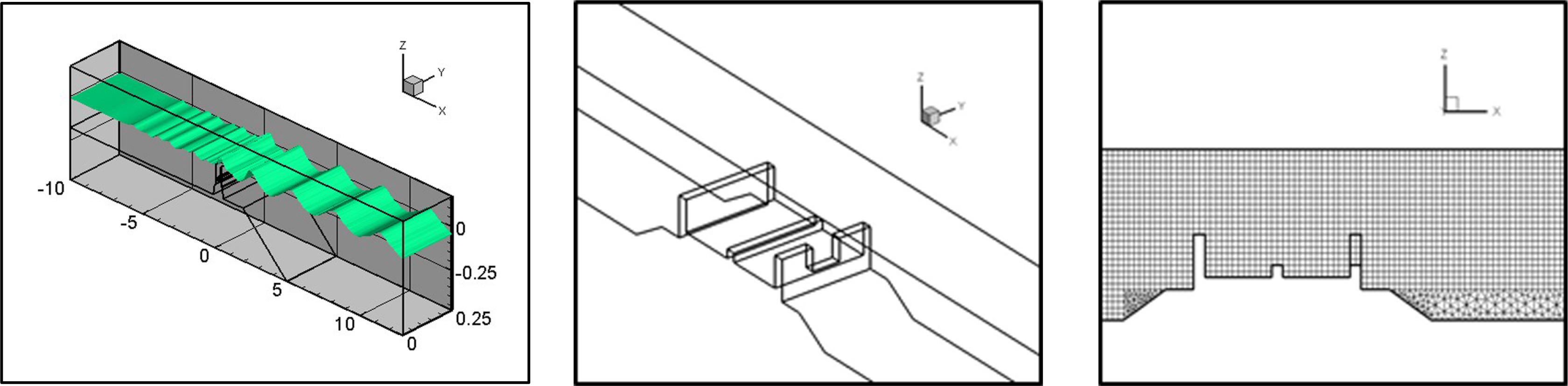
월류식 인공리프의 성능에 대한 수치해석 및 수리실험 결과를 비교 검증하기 위하여, 동일 위치에서 파고변동에 대한 수치해석 및 수리실험 결과를 도시하였다. 입사파 주기 1.58s, 입사파고 7.5cm인 규칙파에 대해 수치해석하였으며, 계산 영역은 Fig. 10과 같이 인공리프 전후로 5파장 정도의 영역을 택하였다. 격자 크기는 인공리프 부근에서는 ∆x, ∆y 및 ∆z를 1.25cm로 인공리프 후면에서는 ∆x를 점차 증가시켜 격자를 분할하였다. 격자는 대부분의 영역은 6면체(Hexagon)의 정렬 격자로 이루어졌으나 실험실 조파수조의 바닥이 경사져 있고 인공리프 전후에 경사면이 있어 6면체의 정렬 격자로 구성하기 어려운 경사면 영역은 5면체(Prism)의 비정렬 격자로 구성하였다. 6면체의 정렬 격자와 5면체의 비정렬 격자로 이루어진 혼합 격자(Hybrid mesh)가 사용되었으며 1,103,820개의 격자로 이루어져 있다.
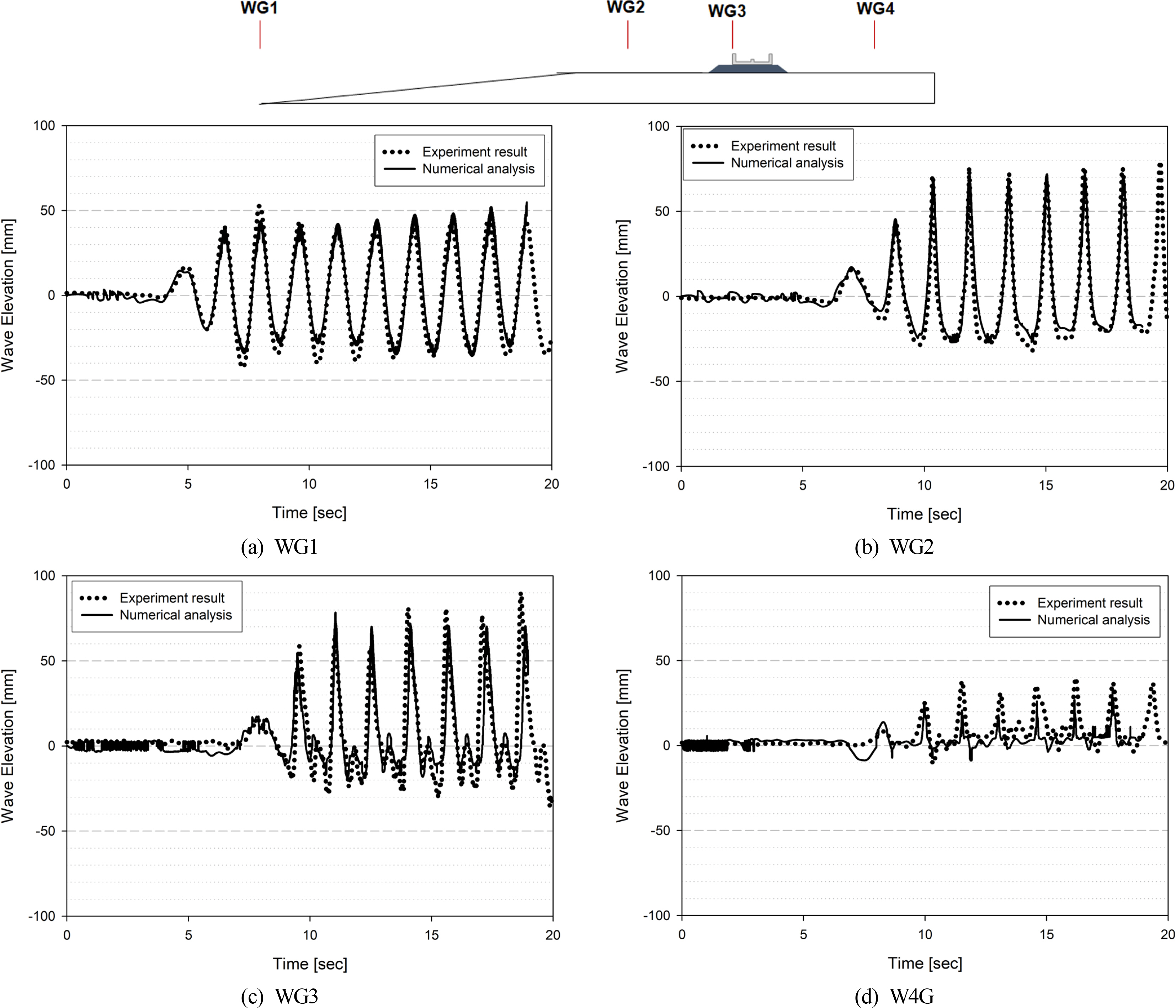
조파기로부터 2.5 파장 위치한 지점(WG1)의 파고를 Fig. 11(a)에 수리실험 결과와 같이 도시하였으며, 그림에서 보듯이 파고와 주기 값이 수치해석 및 수리실험에서 비교적 타당하게 계산되었고 계측되었음을 알 수 있다. 입사파가 해저의 경사면을 따라 진행하면서 수조의 깊이 h=17.5cm로 감소된 수평지점(WG2)에서의 수치해석 결과와 실험 결과는 Fig. 11(b)에 도시하였다. 수조 깊이의 감소에 따라 파곡(Wave trough)는 완만해지며 파정부(Wave crest)는 증가하면서 뾰죽한 형상으로 변화된 비선형 파의 형상이 잘 나타나고 있으며 수치해석 결과와 실험 결과가 비교적 좋은 일치를 보여주고 있다.
Fig. 11(c)에는 입사파가 인공리프와 충돌하게 되는 첫 번째 월류벽에 위치한 개구부에서의 수치해석 결과와 실험 결과의 수면변위를 도시하였는데 정점 WG1 및 WG2와 같이 파곡 및 파정에서의 피크 값이 비교적 일치하고 있음을 보여주고 있으며 특히 파곡에서의 2차 진동하는 형상도 두 결과가 비교적 잘 일치하는 것을 알 수 있다. 그리고 Fig. 11(d)에는 월류형 인공리프 배후 1.5m에서 전달파의 수면변동을 나타내었으며, 수치해석 및 수리실험의 결과 대체로 잘 일치하고 있음을 보이고 있다.
파장 변화에 따른 월류형 인공리프 유동 수치해석 결과를 살펴보면 입사파가 인공리프에 도달함에 따라 개구부가 있는 전면 돌출부에서 일차 쇄파가 이루어지고 이후 감쇄된 입사파가 후면 돌출부에서 이차 쇄파가 이루어지는데 개구부로 인하여 전면 돌출부에서는 일차 쇄파가 다소 미약하게 이루어지며 전체적으로는 2단계의 쇄파 작용으로 구성되는 구조이다(Shin et al, 2018).
월류형 인공리프의 파랑감쇠 원리는 전술한 바와 같이 입사파 에너지를 월류벽에서 강제쇄파를 통한 소산하며, 전면 월류벽에 개구부를 설치하여 개구부가 이안수로(Rip channel) 형태가 되어 외해측으로 흐름을 발생시키도록 고안한 것이다. 따라서 월류형 인공리프내에서 쇄파에 의한 흐름이 복잡하게 나타나며 특히 월류제 개구부 및 내부에서의 시간에 따른 유동 특성을 파악하기 위해서 개구부의 중앙부에서 유속계를 통해 유속을 측정하여 Fig. 12와 같이 수치해석의 결과와 비교 검토하였다.
개구부는 30%이고 입사파 H=7.5cm, T=1.58s에 대해 비교 검토하였으며, Fig. 12에서 +방향은 향안류, -방향은 외해측 흐름을, 그림에서 점선은 수리실험결과를 그리고 실선은 수치실험 결과를 나타내고 있다. 그림에서 보듯이 개구부 중앙부에서 외해측 흐름 및 향안류의 흐름 특성이 주기적으로 나타나고 있으며 유속의 크기 또한 대체로 잘 일치하고 있음을 알 수 있다. 수리실험 결과 외해측 흐름은 최대 유속 U=-0.5m/s, 향안류는 뾰족한 모양의 유속이 주기적으로 나타나며 최대 U=+0.7m/s로 외해측 흐름 유속이 상대적으로 작으나 지속시간이 다소 증가하는 경향을 보이고 있다. 수치실험결과에서는 향안류에서는 유속의 크기가 매우 유사하나 외해측 흐름은 U=-0.41m/s로 상대적으로 낮은 값을 보이고 있으며, 이의 원인은 격자의 크기 및 시간간격 등에 의한 것으로 판단되며 이에 대한 정밀한 수치연구가 필요한 것으로 판단된다.
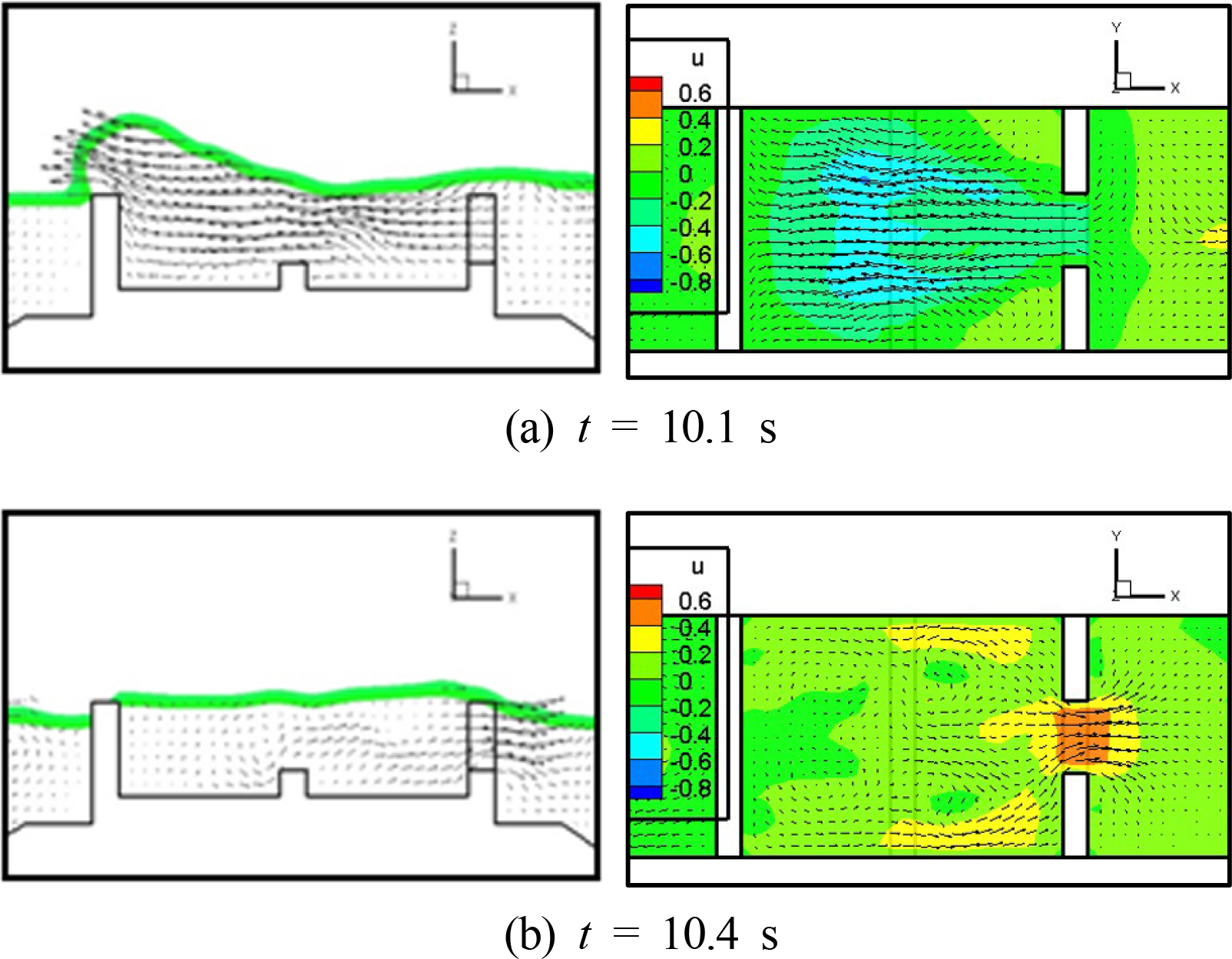
또 Fig. 13에는 월류형 인공리프 내⋅외부의 파랑변동 및 유동특성에 대한 수치해석 결과를 나타내었는데 좌측에는 중앙 단면에서의 속도장을 우측에는 수심 3.75cm 단면에서의 속도장을 도시하였다. 여기서 t=10.1s는 내부에서 향안류가, t=10.4s는 외해측 흐름이 발생하는 경우에 대해 나타내었으며, 파의 위상에 따른 인공리프 내⋅외부의 평면적인 유동특성을 잘 재현하고 있음을 알 수 있다.
유동실험으로부터 개구부를 통한 쇄파에 의한 흐름의 외해측 이동특성이 강하게 발생되는 것으로 확인하였으며, 이를 통해 전달계수의 감쇠에 영향을 미친 것으로 판단되었다. 본 수치결과의 정량적인 검증을 위해서는 PIV(Particle Image velocimetry)기법 등을 통한 검토가 요구되며, 이에 대해서는 계속적인 연구가 필요하다.
본 연구에서는 상대적으로 마루폭이 짧은 월류식 인공리프 주위의 파랑전달 및 흐름 등의 해안수리학적 변동 특성을 수리실험 및 수치해석을 통해 비교 검토하였으며, 대체로 타당한 결과를 확인할 수 있었다. 본 연구에서 제시한 개구부가 있는 월류식 인공리프가 최대 80% 정도의 파고저감 성능을 보여주고 있어 기존 광폭잠제에 비해 마루폭이 짧으면서도 우수한 소파성능을 보이고 있음을 확인할 수 있었다.
월류형 인공리프의 파랑감쇠 원리는 입사파를 전⋅후면 월류벽에서 강제쇄파를 통한 소산하는 것이며, 파랑변동에 대한 수치해석 및 수리실험 결과는 비교적 좋은 일치를 보여주고 있으며, 특히 인공리프 개구부에서의 파곡 및 파정에서의 피크 값과 파곡에서의 2차 진동 형상도 대체로 잘 일치하고 있음을 확인하였다.
그리고 전면 월류벽에 설치된 개구부에서의 시간에 따른 유동 특성을 수치해석 및 수리실험결과를 비교하였으며, 개구부를 통한 외해측 흐름이 강하게 나타나고 있음을 확인하였다. 또한 파의 위상에 따른 인공리프 내⋅외부의 평면적인 유동특성을 재현하여, 배후의 파랑감쇠 특성과 외해류의 관계를 예측할 수 있었다.
본 수치결과의 평면적 유동특성에 대한 정량적인 검증을 위해서는 PIV(Particle image velocimetry)기법 등을 통한 영상해석법에 의한 검토가 요구되며, 이에 대해서는 계속적인 연구가 필요하며, 수치기법의 정밀화를 위한 추가 검토와 함께 평면적인 파랑장 및 유동장 변동 특성과 인공리프 배후의 수면변동에 관한 연구가 계속되어야 할 것으로 판단된다.
Fig. 5
Transmission coef.(KT) as a function of relative mound width (l/L) (Kakemizu and Kimura, 2005)
References
Higuera, P., Losada, IJ., & Lara, JL. (2015). Three-Dimensional Numerical Wave Generation with Moving Boundaries. Coastal Engineering, 101, 35-47. https://doi.org/10.1016/j.coastaleng.2015.04.003

Hong, CB., Shin, YS., & Lee, SD. (2017). Effects of Wave and Current Reduction around the Artificial Reef of Overflow Type. Proceedings of Conference of Korean Coastal Disaster Prevention.
Hur, DS., & Lee, WD. (2007). Three Dimensional Flow Characteristics and Wave Height Distribution around Permeable Submerged Breakwaters. Journal of The Korean Society of Civil Engineers, 27(6B), 689-701.
Hur, DS., Lee, WD., Ahn, SW., & Park, JB. (2010). A Numerical Study on Flow Control Structure of a New-Type Submerged Breakwater. Journal of Korean Society of Coastal and Ocean Engineers, 22(3), 181-190.
Hur, DS., Lee, WD., Goo, NH., Jeon, HS., & Jeong, YM. (2017). Development of New Type of Submerged Breakwater for Reducing Mean Water Level behind Structure. Journal of Ocean Engineering Technology, 31(2), 130-140. https://doi.org/10.5574/KSOE.2017.31.2.130


Kakemizu, N., & Kimura, K. (2005). Hydraulic Performances of Artificial Reef Armored by Cone Shape Block with Horizontal Plate. Proceedings of 62th Conference of JSCE Hokkaido Japan.
Lee, DS., Oh, SH., Park, YD., & Jeong, WM. (2013). Study on the Basic Design Method of Submerged Breakwater Composed of Double-Layer Permeable Blocks. Journal of Korean Society of Coastal and Ocean Engineers, 25(3), 172-180. https://doi.org/10.9765/KSCOE.2013.25.3.172


Lee, KH., Bae, JH., An, SW., & Kim, DS. (2017). Characteristics of Velocity Fields around 3-Dimensional Permeable Submerged Breakwaters under the Conditions of Salient Formation. Journal of Korean Society of Coastal and Ocean Engineers, 29(6), 399-409. https://doi.org/10.9765/KSCOE.2017.29.6.399


Lopez, J., Hernandez, J., Gomez, P., & Faura, F. (2005). An Improved PIIC-VOF Method for Tracking Thin Fluid Structures in Incompressible Two-Phase Flows. Journal of Computational Physics, 208(1), 51-74. https://doi.org/10.1016/j.jcp.2005.01.031



National Association of Sea Coast. (2004). Design Manual of Artificial Reef, Revised Edition National Association of Sea Coast, Japan. p 95.
Peng, D., Merriman, B., Osher, S., Zhao, H., & Kang, M. (1999). A PDE-Based Fast Local Level Set Method. Journal of Computational Physics, 155(2), 410-438. https://doi.org/10.1006/jcph.1999.6345

Sherman, FS. (1990). Viscous Flow. McGraw-Hill.
Shin, YS. (2012). Numerical Analysis of Viscous Flows on Unstructured Grids Using the Optimal Method of Strongly Implicit Procedure. Journal of the Society of Naval Architects of Korea, 49(2), 196-202. https://doi.org/10.3744/SNAK.2012.49.2.196


Shin, YS. (2017). Numerical Analysis of Free Surface Flows Using Adaptable Surface Particle Method based on Grid System. Journal of the Society of Naval Architects of Korea, 54(1), 26-33. https://doi.org/10.3744/SNAK.2017.54.1.26


Shin, YS., Hong, C., & Lee, SD. (2018). Numerical Analysis of Free Surface Movement around the Artificial Reef of Overflow Type. Journal of Coastal Disaster Prevention, 5(1), 1-7. http://doi.org/10.20481/kscdp.2018.5.1.1

Shin, YS., & Lee, SD. (2014). Numerical Analysis of Turbid Flow Considering Density Variation in Reservoir. Journal of the Korean Society of Hazard Mitigation, 14(5), 311-316. https://doi.org/10.9798/KOSHAM.2014.14.5.311

Sussman, M., Fatemi, E., Smereka, P., & Osher, S. (1998). An Improved Level Set Method for Incompressible Two-Phase Flows. Computers & Fluids, 27(5–6), 663-680. https://doi.org/10.1016/S0045-7930(97)00053-4

- TOOLS
-
METRICS

-
- 1 Crossref
- Scopus
- 5,144 View
- 56 Download
- Related articles in JOET
-
Characteristics of Ocean Wave Radiation Patterns in a Dense Layer of Fluid2019 February;33(1)
Motion Characteristics for Submarine Sections m Beam Sea2005 October;19(5)
Flow Characteristics Study around Two Vertical Cylinders2005 February;19(1)
Deformation Characteristics of Compound Curved Plate Bending by Asymmetric Rollers2002 April;16(2)